尼雅水庫壩料動力特性研究及三維地震反應分析

何建新，王 景，楊海華

(1.新疆農業大學水利與土木工程學院，新疆 烏魯木齊 830052；2.新疆水利工程安全與水災害防治重點實驗室，新疆 烏魯木齊 830052)

新疆尼雅水庫位于尼雅河中上游河段，大壩為碾壓式瀝青混凝土心墻壩，最大壩高131.8 m，具有防洪、灌溉、發電等綜合利用功能，其安全穩定對社會發展至關重要。新疆地區地震頻發，震源淺，強度大。因此，在尼雅大壩設計時采用“金包銀”結構。典型設計斷面圖如圖1所示，壩體外部采用堆石料填筑，內部采用砂礫料填筑，心墻兩側采用細級配的砂礫料充當過渡料進行填筑。筑壩材料的動力特性直接影響大壩的抗震性能，因此研究筑壩材料動力特性并對大壩進行動力分析計算。

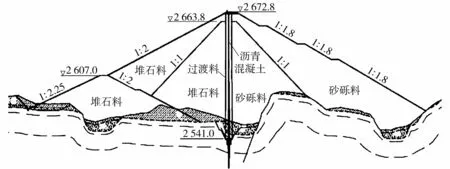
圖1 尼雅水庫大壩典型斷面(單位：m)

我國已建和擬建的百米以上高土石壩近百座，且大多位于高地震烈度區，這些高壩一旦因地震失事，后果將是災難性的，因此對高土石壩的地震安全應十分重視[1]。隨著高土石壩建設的快速發展，壩料的動力特性成為巖土工程研究的重要課題之一。目前，已有學者對大壩地震安全的研究主要集中在壩料的動模量和阻尼比，以及材料本構模型方面，個別學者考慮了覆蓋層的影響。凌華等[2]對筑壩堆石料進行了動力變形特性試驗，分析了圍壓和固結比對最大動模量、動模量衰減規律和阻尼比的影響；楊杰等[3]基于量子遺傳算法(QGA)和支持向量機(SVM)建立細觀參數標定模型；沈珠江等[4]對吉林臺面板壩兩種堆石料進行動力試驗，采用動應力-動應變骨干曲線為雙曲線的假定，提出符合堆石料的動本構模型；朱晟等[5-6]通過復雜高應力條件下粗粒土動力試驗，提出反映材料振動硬化特性的冪函數型動應力-應變關系模型和阻尼比計算公式，同時基于瀝青混凝土的動三軸試驗，建立計算模型，對瀝青心墻壩進行動力分析；房恩澤等[7-8]研究了不同圍壓、孔隙比和固結比等對堆石料模量阻尼比特性的影響，并改進沈珠江模型的殘余剪應變計算公式；鄒德高等[9]對筑壩堆石料的動力殘余變形特性進行研究，并對沈珠江模型進行了改進。本文基于室內動三軸試驗，研究瀝青混凝土心墻壩筑壩材料動力變形特性，并借助三維有限元進行動力分析，深入探討壩體遭遇實際地震作用時的應力-應變關系及永久變形特性，進一步研究瀝青混凝土心墻壩的抗震特性，試驗結果可供大壩的結構穩定設計和安全施工參考。

1 壩料動模量和阻尼比試驗

1.1 試驗方法

采用WYS-2000大型多功能動靜三軸試驗機(圖2)對壩料進行動力特性試驗。該儀器主要技術參數如下：最大軸向靜荷載2 000 kN；最大軸向動荷載1 000 kN；最大圍壓5.0 MPa；最大反壓力2.0 MPa；最大軸向行程400 mm；動荷載頻率0.01～10 Hz。試樣尺寸為?300 mm×700 mm。由于現場填筑的壩料最大直徑為600 mm，依據GB/T 50123—2019《土工試驗方法標準》，通過等量替代和相似級配的方法將壩料進行縮尺，以滿足室內試驗要求，試驗級配曲線如圖3所示。本次試驗選取的固結應力比Kc分別為1.5和2.0，在圍壓分別為0.4 MPa、1.0 MPa和1.6 MPa下進行試驗。

圖2 WYS-2000大型多功能動靜三軸試驗機

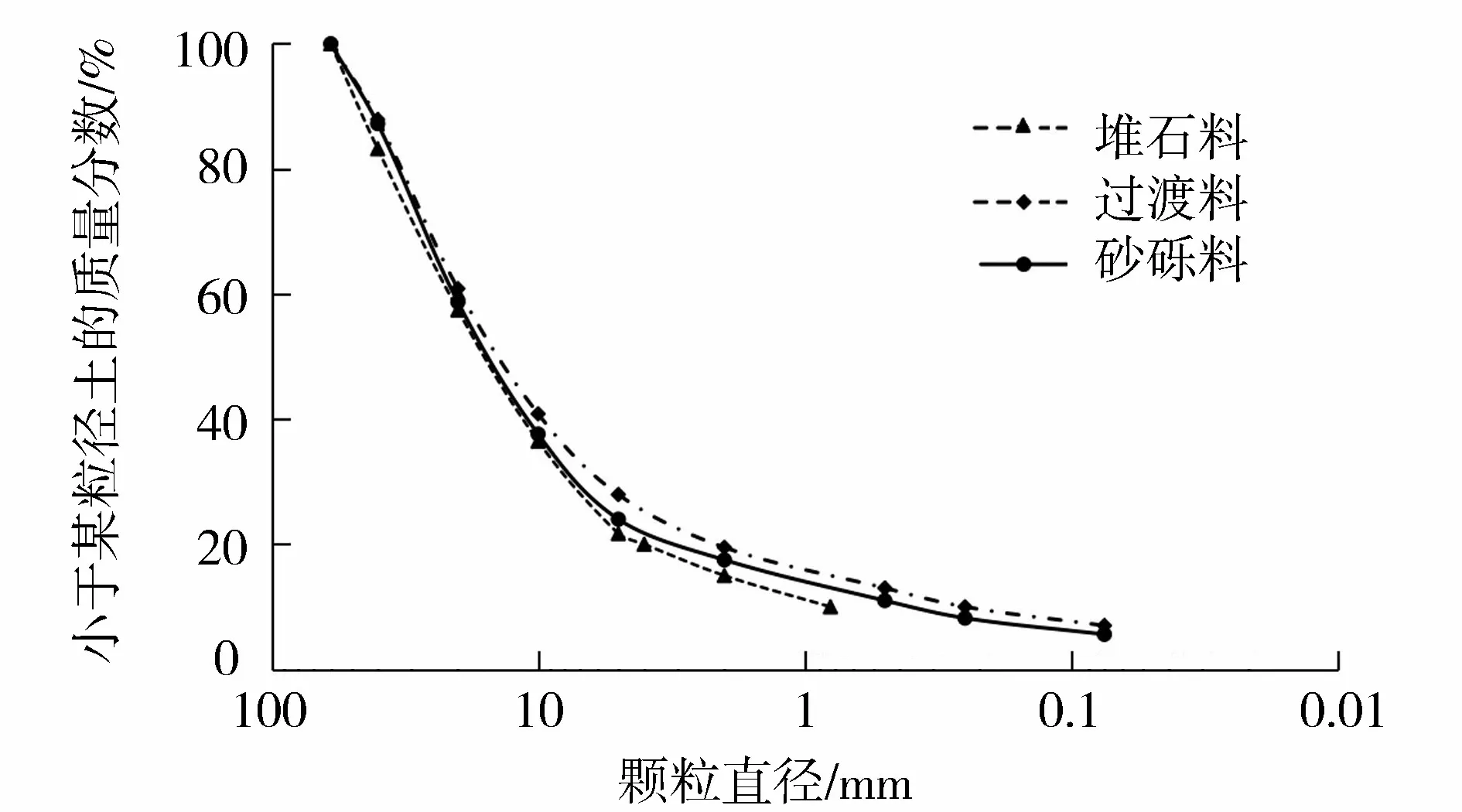
圖3 試驗級配曲線

1.2 結果與分析

根據等效線性黏-彈性模型[10](Hardin-Drenevich模型)，假定動荷載作用下應力-應變曲線為雙曲線，對壩料試驗結果進行分析。砂礫料、過渡料及堆石料動剪切模量Gd與動剪切應變關系曲線γd如圖4所示。由圖4可知，γd在10-4～10-2之間變化，Gd隨著γd的增大而減小，且圍壓和固結比的變化對Gd影響較大。固結比相同時，圍壓越大，壩料在固結時被擠壓越密實，壩料的Gd隨著圍壓的增大而增大。圍壓相同時，固結比越大，試樣中的土顆粒同樣會被擠壓密實，Gd增大。工程建設中的堆石料多為巖石風化或山體經爆破后得到的尖角料，固結時由于顆粒間的擠壓和摩擦會產生顆粒破碎現象，從而使原級配發生改變。而砂礫料是經水流沖擊搬運等作用形成的以圓形或亞圓形為主的級配料，顆粒強度較高。由試驗結果可知砂礫料和過渡料的最大動剪切模量比堆石料高4%～11%，砂礫料和過渡料抵抗變形的能力優于堆石料。

圖4 不同固結比、圍壓下壩料Gd-γd關系曲線

Hardin等[10]認為阻尼比與動應變也呈雙曲線關系。圖5為Kc=1.5時不同圍壓下3種壩料λ-γd關系曲線，由圖5可知，圍壓對壩料阻尼比的影響較大，3種壩料的阻尼比均隨著圍壓的增大而減小，且隨著圍壓的增大，壩料阻尼比的增長越緩慢[11-14]。統計3種壩料在不同固結比作用下的最大阻尼比λdmax，如表1所示。由圖5和表1可知，3種壩料的阻尼比隨著動剪切應變的增大而增大，由于過渡料的細顆粒含量高于砂礫料中細顆粒含量，相同固結比作用下過渡料的最大阻尼比高于砂礫料。堆石料為巖體爆破級配料，顆粒表面以棱角形為主，受壓后顆粒間發生錯動摩擦使棱角破碎，導致原級配改變，且圍壓越大，顆粒破碎越明顯，故堆石料的最大阻尼比比砂礫料和過渡料高4%～14%，堆石料吸收的應變能高于砂礫料和過渡料。根據設計，在外側填筑堆石料有利于壩體適應變形和維持邊坡穩定。

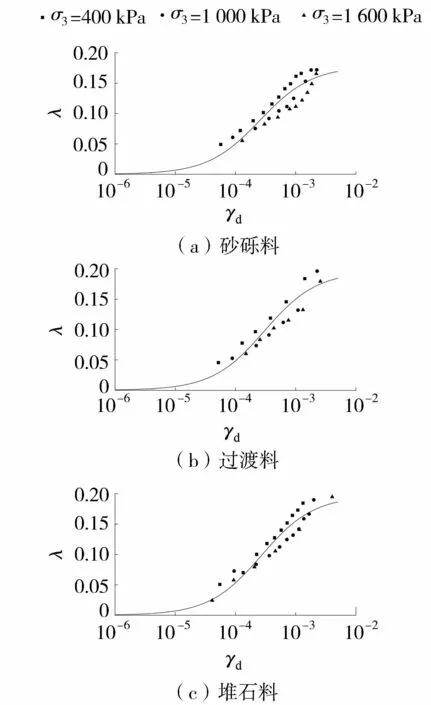
圖5 不同圍壓下壩料λ-γd關系曲線(Kc=1.5)

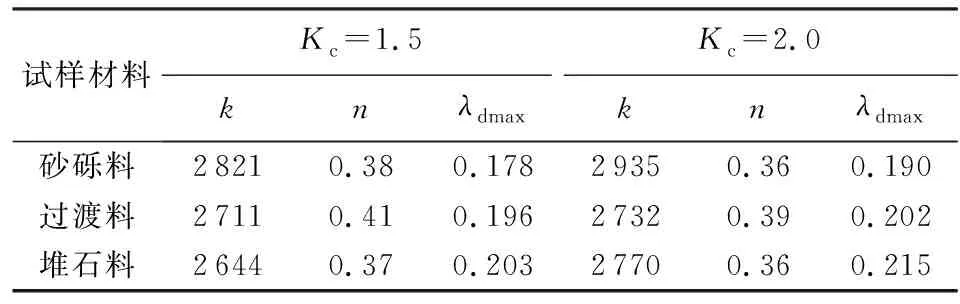
表1 動剪切模量系數、指數和最大阻尼比

根據動三軸試驗得到歸一化的動剪切模量Gd/Gdmax和等效阻尼比λ如表2、表3所示，可知動剪切模量和阻尼比具有良好的歸一性，試驗結果可靠。

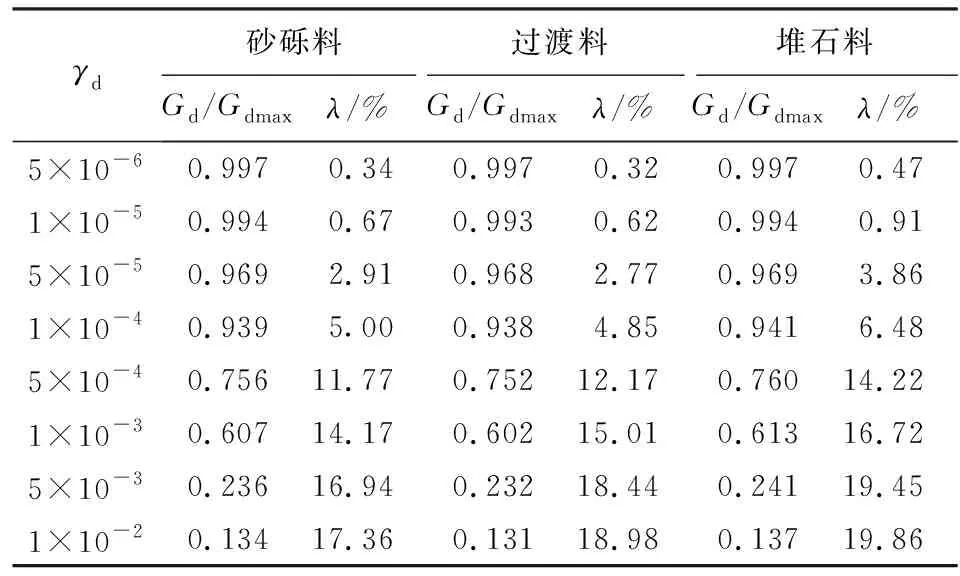
表2 Kc=1.5時歸一化的動剪切模量和等效阻尼比

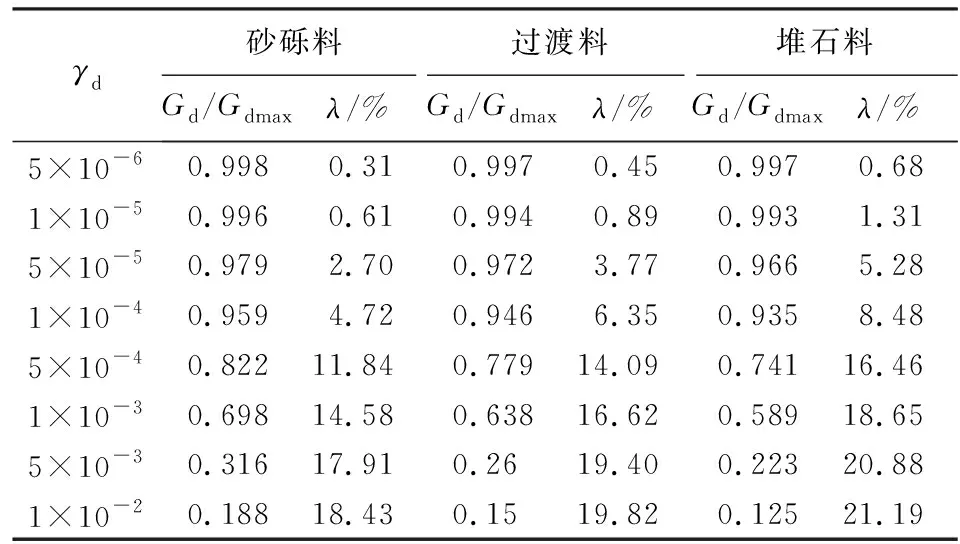
表3 Kc=2.0時歸一化的動剪切模量和等效阻尼比

2 壩料永久變形試驗

本次永久變形試驗共選擇2種固結比，3種應力比，按Kc=1.5、σd/σ3=0.5和Kc=2.0、σd/σ3=1.0這2種主要組合進行永久變形試驗。試驗結果采用大連理工大學鄒德高等[15-16]提出的雙曲線模型進行整理，壩料殘余剪切應變γr與振次N的關系曲線如圖6所示。一般而言，循環動應力下粗粒料的殘余剪應變與固結比、圍壓和振次等因素有關。由圖6可知，固結比和圍壓越大，壩料的殘余剪切應變越大，初始固結比和圍壓的增大都會提高試樣的密實度，骨料接觸更加緊密；隨著振次的增加，壩料的殘余剪應變不斷增加，但其變化速率不斷減小，符合衰減規律；由于顆粒破碎效應，堆石料的殘余剪切應變明顯高于砂礫料和過渡料。

圖6 壩料γr-N關系曲線

3 心墻瀝青混凝土動力特性試驗

3.1 試驗方法

根據《尼雅水庫堿性骨料瀝青配合比報告》[17]，本工程心墻瀝青混凝土配合比優選后基礎配合比如表4所示。制備?100 mm×200 mm的瀝青混凝土三軸試件，本次試驗選取的固結應力比分別為Kc=1.5、1.8、2.1，在圍壓σ3分別為0.2 MPa、0.6 MPa和1.0 MPa下進行試驗。

表4 瀝青混凝土設計優選配合比

3.2 結果與分析

根據Hardin-Drenevich模型，對心墻瀝青混凝土動三軸試驗結果整理如表5所示。圍壓和固結應力比對心墻瀝青混凝土的最大動模量Edmax和最大動剪切模量Gdmax的影響較大。固結應力比相同時，隨著圍壓的增大，瀝青混凝土的Edmax和Gdmax增大，但其增幅減小。圍壓相同時，隨著初始固結應力比增大，瀝青混凝土材料的Edmax和Gdmax不斷增大，初始固結應力比增大使瀝青混凝土更加密實，從而提高材料的剛度。

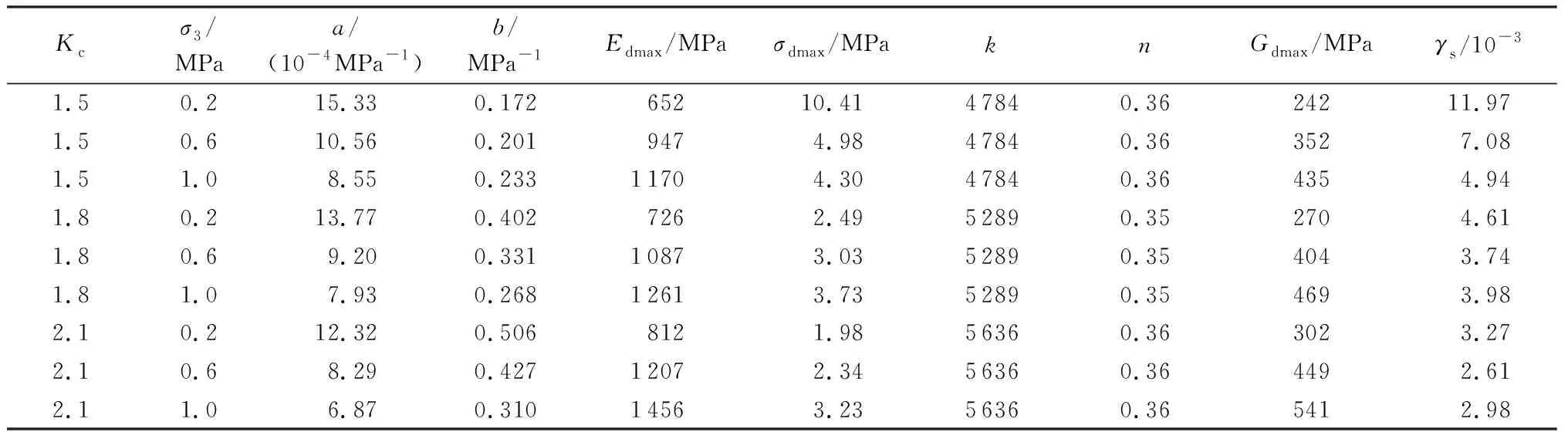
表5 心墻瀝青混凝土動三軸試驗結果

4 動力分析計算

尼雅大壩壩址處中、小地震相對活躍，周邊破壞性地震對場地的最大影響烈度為Ⅶ度，因此分析大壩在地震作用下的動力、變形特性和安全穩定性。

4.1 計算軟件介紹

本次三維地震動力反應分析采用大連理工大學自主開發的巖土工程三維靜、動力有效應力非線性分析程序GEODYNA極限平衡法穩定計算軟件GEOSTABLE和有限元動力法邊坡穩定和變形分析軟件FEMSTABLE。GEODYNA包含多種連續介質本構模型和接觸面模型；GEOSTABLE包含瑞典法和簡化Bishop法，可考慮線性強度和非線性強度；FEMSTABLE采用有限元擬靜力法和動力法計算土坡穩定安全系數，具有動態滑弧顯示功能，可考慮線性強度和非線性強度。

4.2 計算模型及參數

4.2.1幾何模型

根據壩體設計橫斷面，同時考慮該工程復雜的河谷地形條件、大壩材料分區以及分層填筑對大壩應力和變形的影響，建立壩體三維有限元網格如圖7所示，瀝青混凝土心墻三維有限元網格如圖8所示。壩體三維有限元模型單元數為289 831個，節點數為336 612個，自由度超過106。瀝青混凝土心墻三維有限元模型單元數為6 689個，節點數為13 822個，壩體典型橫斷面材料分區如圖1所示。

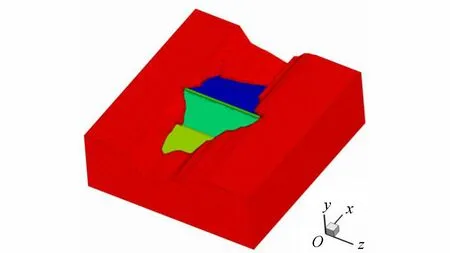
圖7 壩體三維有限元網格

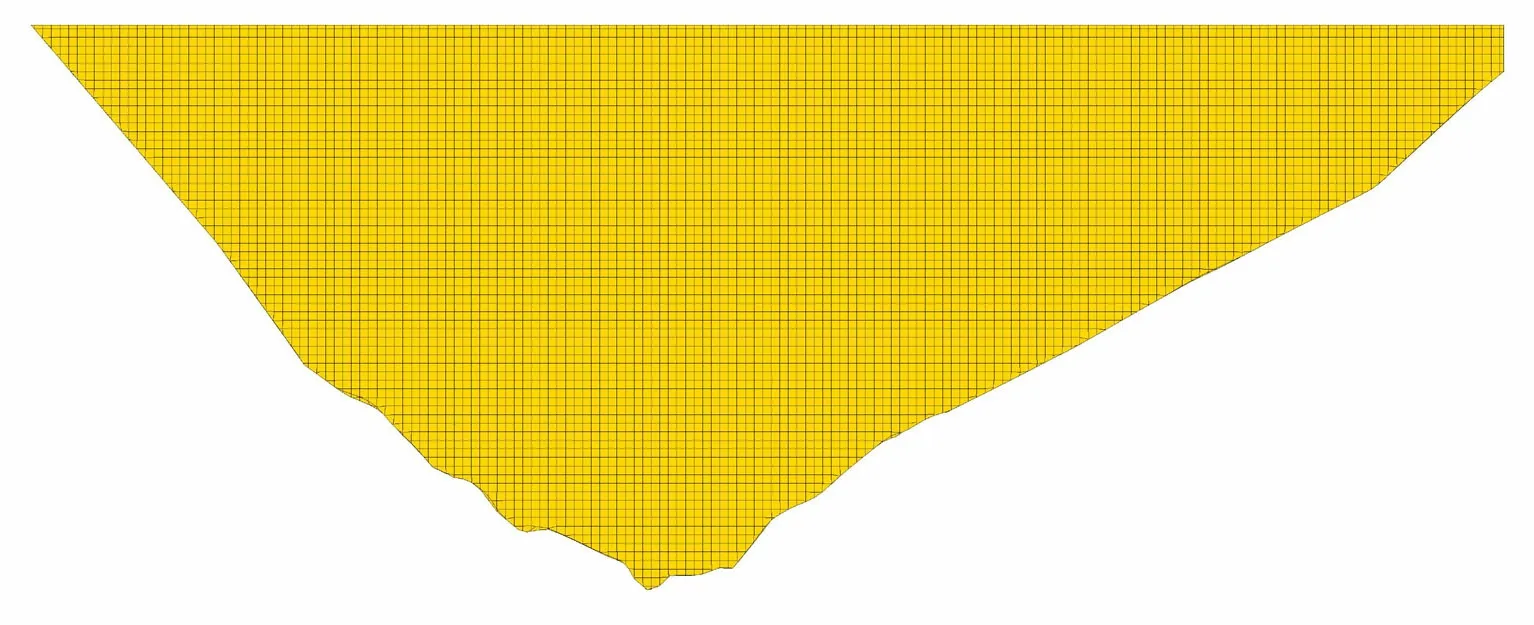
圖8 心墻三維有限元網格

4.2.2動力計算本構模型

4.2.2.1 壩料

筑壩材料動力計算本構模型采用等效線性黏-彈性模型，筑壩材料最大動剪切模量表示為

(1)

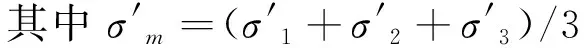
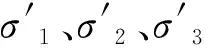
4.2.2.2 接觸面

接觸面單元的動力模型中，接觸面的最大動剪模量為

(2)

式中：σn為接觸面單元的法向應力；C為接觸面動力剪切試驗測得的系數，取22.0。

接觸面單元的剪切勁度K與動剪應變γ的關系如下：

(3)

其中τf=σntanδ

式中：τf為破壞剪應力;δ為接觸面的摩擦角;參數M=2.0。

接觸面單元的阻尼比λ為

(4)

式中：λmax為最大阻尼比，計算中取0.2。

4.2.2.3 地震永久變形計算模型

土石壩地震永久變形分析采用以應變勢概念為基礎的整體變形計算方法。以往的殘余變形模型假定殘余應變與振次在半對數坐標下呈線性關系。但殘余體應變與振次的關系曲線在半對數坐標下并不是簡單的線性關系，初期的體積應變慢于半對數變化規律。采用半對數線性關系會明顯低估較大振次處的殘余體應變，圍壓和動應力越大差別越明顯，對分析大壩的安全不利。大連理工大學鄒德高等[9,15-18]通過研究多種壩料的永久變形試驗成果，提出了大工雙曲線殘余變形模型，該模型的殘余體應變和剪應變分別表示為

(5)

(6)

式中：εvr為殘余體應變；γr為殘余剪應變；Asr為極限的殘余剪應變；Bvr和Bsr均為與材料有關的常數。

為避免高估壩頂處體積收縮變形的問題，該模型引入了平均主應力反映殘余體積變形規律。將極限狀態下的殘余體應變εvr表示為平均主應力和動剪應變的函數：

(7)

式中：d1、d2為模型參數；σ0為平均主應力。

對于砂礫料，將Asr表示為動剪應變的函數：

(8)

式中：d3、d4均為模型參數。

4.2.3計算參數

以室內動力三軸試驗結果作為本次大壩動力分析的計算參數，壩料動模量和阻尼比參數見表1至表3，心墻瀝青混凝土動力參數如表5所示，永久變形計算參數如表6所示。

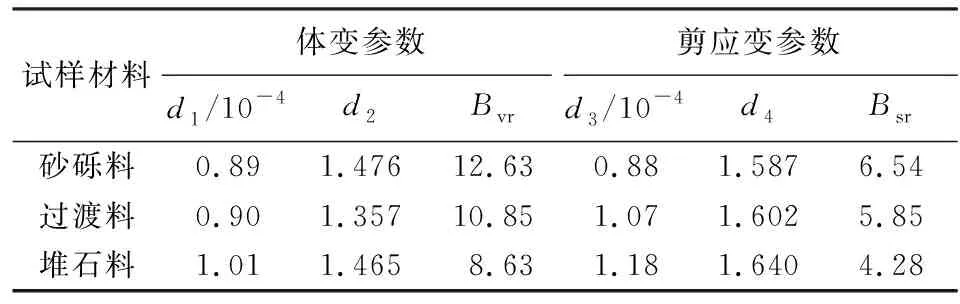
表6 永久變形計算參數

4.2.4地震動輸入

高土石壩-河谷山體系統是一個能量開放的系統，山體河谷與壩體之間存在著不同程度的相互作用，外行的散射能量會向無限地基輻射。這些因素會導致壩體邊界處各點的反應幅值及相位存在差異，使地震波動效應的影響更加顯著。因此，本次有限元計算地震動輸入采用黏彈性邊界和等效荷載，考慮了大壩和基巖的動力相互作用及輻射阻尼[19]。根據壩址場地地震動參數和GB 51247—2018《水工建筑物抗震設計規范》對標準設計反應譜的規定擬合得到地震時程曲線。設計地震動水平向峰值加速度為0.139g，豎向峰值加速度為水平向的2/3，順河向、豎向和壩軸向的地震加速度時程曲線如圖9所示。動力計算時在模型底部和側邊施加黏彈性邊界，以模擬地基無限域輻射阻尼的作用。人工邊界通過在邊界節點上施加切向和法向的阻尼器來實現，其參數可分別按下式計算：

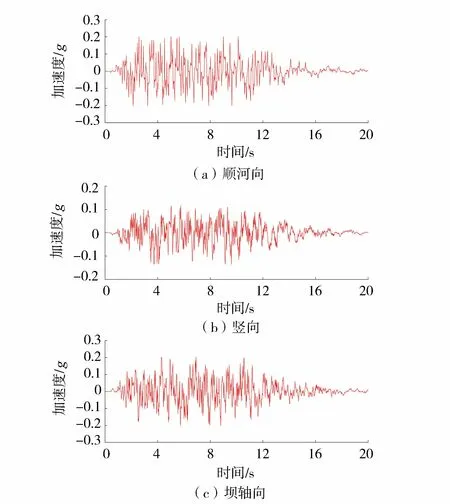
圖9 設計地震時程曲線

Ct=ρVsΔAi

(9)

Cn=ρVpΔAi

(10)

式中：ΔAi為模型外邊界節點i的控制面積(亦稱代表面積)；ρ為節點i處邊界材料的密度；Vs、Vp分別對應節點i處邊界材料的剪切波速與縱波波速。

4.3 地震動力反應

4.3.1壩體地震反應

壩體各方向動力反應后動位移三維分布如圖10所示，加速度三維分布如圖11所示，動力反應后的計算結果見表7。由圖10可知，隨著壩高的增大，壩體各方向的動位移增大。壩體順河向最大動位移為0.042 m，豎向最大動位移為 0.014 m，壩軸向最大動位移為0.028 m，最大值均出現在壩頂附近。壩體左岸和右岸動位移近似相等且關于壩體中心斷面對稱。由于河谷基礎的約束，岸坡處壩體豎向動位移小于壩頂中心處動位移。由圖11可知壩體最大順河向加速度為4.98 m/s2，最大豎向加速度為3.29 m/s2，最大壩軸向加速度為4.02 m/s2，最大值均位于壩頂部附近。順河向、豎向、壩軸向加速度放大倍數分別為3.65、2.41、2.95。根據壩體地震反應結果可知壩體順河向動位移和加速度均最大，地震波可簡化為一個垂直向上傳播的剪切波(S波)和縱波(P波)以及面波(瑞利波與勒夫波)[20]。S波引起剪應力變化，P波引起正應力變化，S波和P波同時作用使壩體水平方向剪應變增大，地震波對壩體順河向的影響最大。

圖10 地震時壩體各方向最大動位移(單位：m)

圖11 地震時壩體各方向加速度(單位：m/s2)

4.3.2心墻應力

心墻靜動疊加應力如圖12所示，混凝土心墻靜動疊加最大大主應力和最小小主應力均隨著心墻深度的增加而增加，且由于受到岸坡的約束，心墻最大壓應力為2.46 MPa，出現在心墻與岸坡交界處；最大拉應力為0.05 MPa，出現在心墻的頂部和左岸岸坡處；心墻大小主應力的最大值均位于心墻底部，設計施工時需注意心墻底部的抗剪強度。

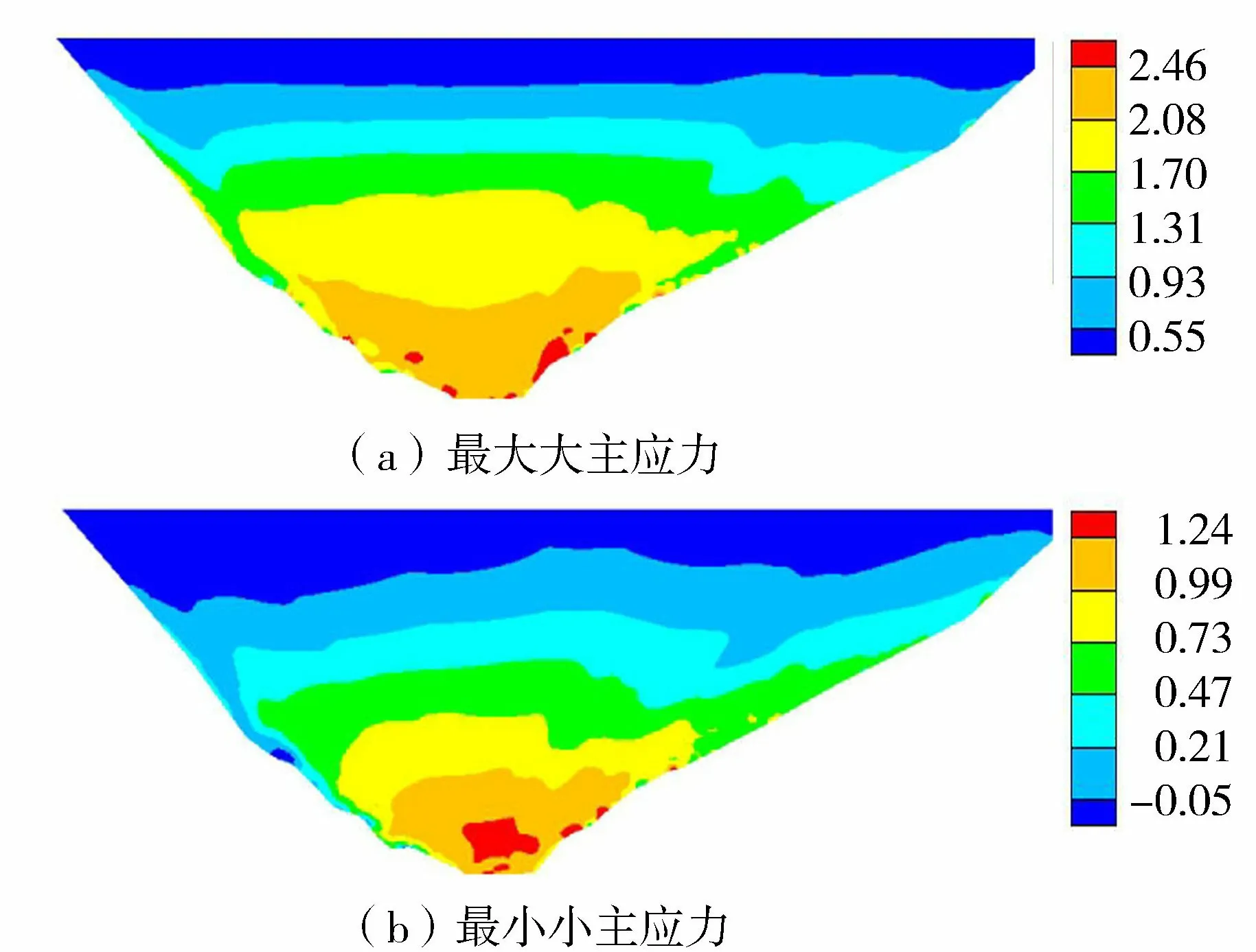
圖12 地震作用時應力(單位MPa，以壓應力為正)

4.3.3壩體永久變形

根據有限元動力分析的計算結果，對壩體進行三維永久變形計算。計算得到的大壩典型斷面位移見圖13。由圖13可知，隨著大壩高度的增加，壩體下游順河向永久位移增加，且位移變形均為向下游。上游最大永久位移位于上游坡1/2壩高處，順河向最大位移為0.035 m(向上游)，下游壩體順河向最大位移在壩頂處，最大位移為0.062 m(向下游)，下游最大位移僅為上游最大位移的1.77倍。由于壩體上下游土體順河向最大永久變形均為背離壩坡方向，土體受到拉應力作用產生順河向永久位移，因此壩體上下游土體順河向均產生拉應力破壞。壩體豎向地震永久變形隨著壩高的增加不斷增大，均表現為垂直沉降，且豎向永久變形云圖表現為層狀結構，即壩高相同時壩體豎向沉降量近似相等，地震時壩體不易發生不均勻沉降引起的結構破壞。壩頂最大沉降為0.107 m，約占壩體和覆蓋層高度的0.084%，該量值在土石壩正常永久變形范圍內，說明“金包銀”結構具有良好的抗震效果。

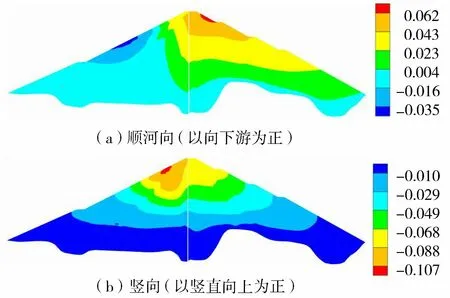
圖13 0+150壩體典型斷面永久變形(單位：m)

4.3.4心墻永久變形

地震永久變形后心墻應力如圖14所示，各方向位移如圖15所示，由于受到岸坡的約束，心墻最大壓應力為1.92 MPa，仍出現在心墻與岸坡交界處，大小主應力均無拉應力產生。震后心墻3個方向的最大位移均發生在壩頂處，隨著心墻高度的增加，心墻豎向永久位移不斷增大，心墻豎向永久位移最大值為0.072 m，比兩側壩體豎向永久位移小0.035 m，心墻與壩體同步適應變形的能力較強。沿壩軸向永久位移最大值為0.020 m，沿順河向永久位移最大值為0.047 m。

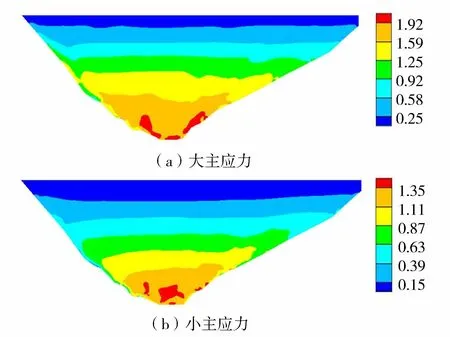
圖14 震后心墻應力(單位：MPa，以壓應力為正)

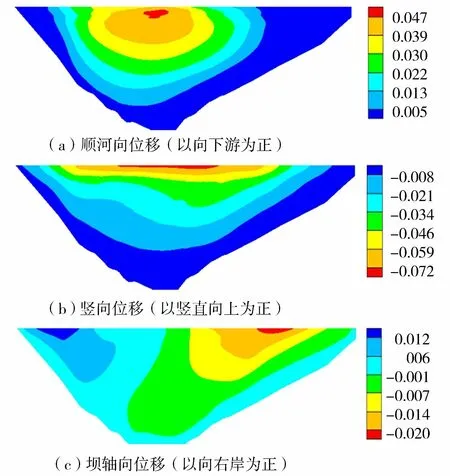
圖15 震后心墻各方向位移(單位：m)

4.4 大壩穩定分析

采用極限平衡法計算大壩典型斷面在正常運用期遭遇地震的壩坡的穩定性。運用期遭遇地震時，在設計地震波為0.139g工況下，大壩典型斷面上游安全系數為2.03，下游安全系數為2.43，安全系數均滿足規范規定的安全系數控制值1.2，壩體具有較高的安全儲備。

5 結 論

a.砂礫料和過渡料的最大動剪切模量比堆石料高4%～11%，砂礫料和過渡料抵抗變形的能力優于堆石料，而堆石料的最大阻尼比比砂礫料和過渡料高4%～14%，堆石料顆粒間發生錯動摩擦產生的應變耗能高于砂礫料和過渡料。

b.圍壓和固結比對心墻瀝青混凝土的最大動模量和最大動剪切模量的影響較大。固結比相同時，隨著圍壓的增大，瀝青混凝土的最大動模量和最大動剪切模量增大，但其增幅減小。圍壓不變時，隨著初始固結比的增大，瀝青混凝土材料更加密實，從而提高了材料的最大動模量和最大動剪切模量。

c.根據地震動力反應，壩體各方向最大位移、加速度和最大永久變形均發生在壩頂處，順河向最大位移為0.042 m，最大加速度為4.98 m/s2，最大沉降為0.107 m，壩體上下游順河向最大永久變形均表現為背離壩坡，順河向可產生拉應力破壞。心墻大小主應力最大值均發生在底部，豎向永久位移最大值為0.072 m，壩體的最大沉降比心墻高0.035 m，壩體與心墻協調變形能力較強。

d.從筑壩材料動力試驗及大壩三維動力分析計算可知，尼雅水庫瀝青混凝土心墻壩采用“金包銀”結構不僅可以有效地利用壩址周邊的砂礫料，節約成本，而且使壩體具有良好的抗震性能。