考慮負荷優化的光儲充電站儲能經濟性配置研究

許 強,王 維,吉同舟,徐衍微

(南京師范大學南瑞電氣與自動化學院,江蘇 南京 210023)

近年來電動汽車(electric vehicle,EV)在節能減排方面相比傳統燃油車有著巨大的優勢,因此得到廣泛推廣. 隨著電動汽車保有量的增加,電動汽車的充電需求逐漸增長,其配套設施建設也日趨完善. 然而,對于一個規模化的公共充電站而言,大量電動汽車同時涌入充電會對電網的安全穩定運行造成較大的影響[1-2]. 加裝儲能裝置能夠有效消除峰谷差[3],平滑功率波動[4-5],提高供電可靠性[6],可以在滿足充電需求的同時減少對電網的影響.

受制于儲能電池價格的影響,儲能系統的配置效益尤為重要. 目前已有大量學者對充電站儲能經濟性配置展開研究. 文獻[7]建立了儲能投資和運營成本模型,研究結果表明在公交車快速充電站配置儲能可以將總成本減小22.85%. 文獻[8]建立了電池壽命損耗模型以尋求充電站儲能的經濟性配置. 文獻[9-10]利用排隊理論評估充電站的合理容量配置. 文獻[11]利用多目標優化模型,計算得到不同光伏配比和充電樁功率等級下的經濟容量. 上述文獻在儲能配置的研究上取得了一定的成果,但是傳統以負荷峰值[8-10]、峰谷差率[11]為優化指標的配置模型中儲能的利用率仍舊偏低,儲能配置的經濟性有進一步提升的空間.

充電站作為電動汽車充電的主要載體之一,站內的充電負荷是儲能配置的關鍵指標,這影響到儲能配置的經濟性. 因此,本文首先分析了充電站電動汽車負荷特性,并且給出峰谷電價場景下儲能充放電策略. 接著以充電站年凈利潤最大為目標,兼顧儲能出力優化,綜合考慮充電站的運營利潤、建設維護成本、政府補貼等因素,建立了基于雙層規劃的儲能配置模型. 最后通過算例求解出充電站最佳容量配置,并將該配置方案與傳統配置方案展開對比,驗證了模型的有效性.

1 光儲充電站結構與電動汽車負荷分析

光儲充電站是實現光伏、儲能、充電互相協調支撐的一種高科技綠色充電站,主要由配電網系統、光伏發電系統、儲能系統、充電樁、AC/DC變換器、DC/DC變換器、能量管理系統等部分組成,其結構如圖1所示.

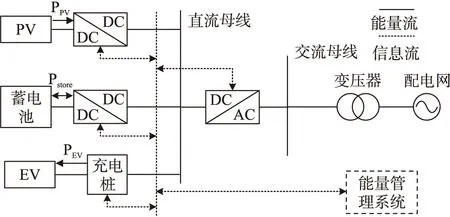
圖1 光儲充電站結構示意圖Fig.1 Structure diagram of photovoltaic and energy-storageintegrated charging station

充電站的電動汽車負荷特性很大程度上影響到儲能容量的配置,所以有必要對充電站的電動汽車負荷進行分析. 文獻[12]的研究結果表明,充電站的負荷與用戶的生活習慣、日常出行規律、行駛里程等關系較為密切. 本文以某商業區公共充電站為例,經過對該充電站的負荷采集發現,該充電站的日負荷分布呈現明顯的規律性. 因此,可以通過對該充電站電動汽車實際的充電負荷進行分析,結合負荷特性對儲能配置展開研究.

圖2給出了某典型日充電站站內電動汽車負荷和商業區基本負荷的分布. 從站內電動汽車負荷的時序分布可知,車站內負荷的高峰期主要集中在上下班之后,表明了充電站負荷與居民生產生活之間的緊密聯系. 接著,由站內電動汽車負荷分布與商業區基本負荷分布的對比可知,充電站站內電動汽車負荷不僅符合居民的日常出行規律,也與商業區基本負荷的峰谷時段基本一致. 商業區基本負荷和充電站日負荷高峰期主要集中在09:00—13:00以及17:00—21:00這兩個時間段,負荷高峰時段的重合會導致該區域配電網“峰上加峰”. 此外,由于充電站實行統一充電價格,負荷高峰期間,充電站購電成本較高,大量電動汽車集中在負荷高峰期間充電,增加了充電站的購電成本,一定程度上影響了充電站的收益. 所以可以利用電網峰谷電價和儲能系統降低充電站負荷對區域配電網的影響,以減少充電站的購電成本.

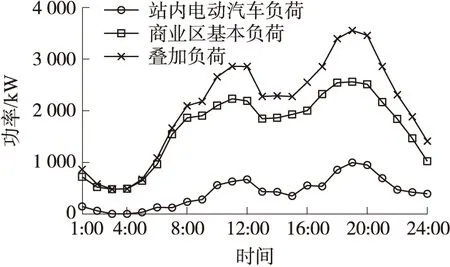
圖2 電動汽車負荷對商業區配電網的影響Fig.2 Influence of EV load on distribution networkin business district

2 峰谷電價下的儲能運行策略

由上一節分析可知,充電站內電動汽車負荷高峰與商業區基本負荷高峰時期重合,結合站內電動汽車負荷特性,為充分發揮儲能系統的經濟效應,本文根據峰谷電價制定了相應的儲能運行策略,策略設計原則如下:(1)合理利用峰谷電價來提升充電站經濟效益. (2)輔助配電網“削峰填谷”,盡可能減小電動汽車負荷對區域配電網的不利影響.

儲能的運行策略如圖3所示. 依據峰谷電價將一天劃分為峰、谷、平3個時段. 充電站能量管理系統實時監測當前時段的電動汽車負荷、光伏出力、儲能單元的荷電狀態(state of charge,SOC). 儲能系統運行策略的核心是“低儲高發”,不同的時段采取不同的運行策略. 在谷時段,充電站負荷與配電網負荷處于較低水平,光伏幾乎沒有出力,此時段電價較低,可以從電網購電,存儲在蓄電池內. 在平時段,儲能的運行狀態參考光伏出力,白天有光伏出力時,儲能盡可能地吸收光伏能量. 如果光伏出力不足,且儲能沒有達到荷電上限,剩下的電能通過電網補充. 夜間無光伏出力時,儲能系統處于浮充狀態,不充電也不放電. 在峰時段,儲能配合光伏,最大化地向電動汽車提供能量.

圖3 儲能運行策略流程圖Fig.3 Flow chart of energy storage operation strategy

3 儲能配置雙層規劃模型

儲能配置既要考慮充電站的投資建設成本,又要考慮儲能系統對電動汽車負荷的優化. 儲能的容量越大,對于電動汽車負荷的平抑效果越好,但是充電站的建設成本也會增加,所以實現充電站儲能系統的經濟運營需要綜合考慮充電站的各項建設成本和收益,以及儲能系統的優化運行. 本節利用雙層規劃理論建立儲能系統優化模型,通過上下層的動態博弈,以獲得充電站儲能配置的最優解.

3.1 上層規劃模型

上層規劃的目標是充電站年收益最大,需要綜合考慮各項成本和收益,主要包括充電站建設成本、維護成本、運營收益、政府補貼4個因素. 上層目標函數Fup為

Fup=max(I-C1-C2+S).

(1)

式中,I表示充電站運營收益年值,C1表示充電站建設成本年值,C2表示充電站維護成本年值,S表示政府補貼. 其中,

(2)

(3)

C2=(CeE+CpPmax)kes+Qpvkpv.

(4)

式(2)表示充電站運營收益,包括光儲系統充放電套利、電網公司對充電站降峰的激勵. 其中,Pev,t和Pl,t分別是電動汽車負荷和充電站負荷凈值,xs、x(t)和xe分別是充電費、t時刻購電電價和峰時段充電站降峰補貼,T表示全天的優化時段數,K表示峰值時段. 考慮到站內日充電負荷和光伏的波動,對于充電站的收益估計取260個近似日[13],等效得到充電站運營利潤年值. 式(3)表示充電站建設成本,其中,Cf為充電站投資固定成本,Cpv為光伏單元單價,Qpv為光伏配置額定容量,Cpile為充電樁單價,n為充電站內充電樁個數,Ce和Cp分別為單位容量儲能電池的價格和功率轉換裝置的單價,E和Pmax分別為儲能系統容量和最大充放電功率,r為貼現率,m1和m2分別為光伏系統壽命年限和儲能系統壽命年限. 式(4)表示充電站維護成本,其中,kes為儲能系統年運行維護系數,kpv為光伏系統年運行維護系數. 此外,儲能系統有政府提供的一次性的建設性補貼[13],假設補貼資金為儲能系統一次性投入的30%.

3.2 下層規劃模型

下層規劃的目標是儲能充放電功率優化,抑制充電站引起的區域配電網峰谷差以及減少充電站的購電成本. 下層規劃模型的目標函數:(1)優化時間段內配電網負荷曲線方差最小. (2)充電站日購電成本最低.

(5)

式中,Ps,t是區域配電網t時刻的負荷值,Pavg是區域配電網一天內負荷曲線的平均值.

下層規劃模型是雙重目標優化問題,可將f1和f2做歸一化處理,將其轉化為單目標函數. 具體方法為

minFdown=min(ω1f1/f1max+ω2f2/f2max).

(6)

式中,f1max是24 h內區域配電網的最大方差,f2max是充電站一天內最大的購電成本,ω1和ω2分別為f1和f2的權重系數,本文設定對于區域配電網的負荷方差和日購電成本同等權重,即ω1=ω2=0.5.

一年體驗數十輛新車，我本應該對試駕車保持專業、理性，甚至是冷淡的態度。但事實證明，這樣的理論對梅賽德斯-奔馳G級越野車沒用，無論新舊，無論貴賤。

3.3 約束條件

(1)功率平衡約束

(7)

式中,Pbase,t為t時刻商業區基本負荷,Ppv,t為t時刻的光伏出力,Pb,t為儲能系統t時刻的充放電功率. 當充放電功率為負時,儲能處于放電狀態,當充放電功率為正時,儲能處于充電狀態.

(2)儲能充放電倍率約束

儲能的充放電倍率為儲能的充放電功率與電池容量的比值,過大的充放電倍率可能會影響儲能電池的壽命. 為了不影響電池的使用,本文設定充放電倍率上限為0.4C,儲能充放電倍率約束表達式為

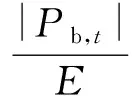
(8)

(3)充放電深度約束

為了防止過度充電或者過度放電對儲能電池壽命產生影響,必須讓儲能電池運行在合適的荷電范圍內.

SOCmin≤SOCt≤SOCmax.

(9)

(4)荷電狀態連續性約束

(10)

式中,λ為儲能系統的充放電效率.

4 算例分析

4.1 算例參數說明

圖4 典型日光伏出力曲線Fig.4 Typical daily curve of photovoltaic

光儲充電站作為電動汽車充電服務的提供者,其運營模式主要是按照峰谷電價從電網購電,再按照設定的價格收取用戶的充電費,運營商從中間賺取差價盈利. 峰谷電價設定參考江蘇省大工業用電電價,電動汽車充電費用參考南京市棲霞區某充電站充電電價,電價設定如表1所示. 此外,為響應電網削峰填谷的號召,為充電站設置一定的降峰補貼,本文假設降峰補貼為0.2元/kWh.

表1 電價參數設置Table 1 Parameter setting of energy price

4.2 優化結果分析

4.2.1 儲能容量配置

當儲能容量配置不同時,儲能的負荷優化能力也會有差異,這直接影響到充電站的收益. 仿真計算了充電站儲能容量配置在0～1 500 kWh之間的收益分布情況,迭代間隔為10 kWh,計算結果如圖5所示. 由于粒子群算法在求解全局最優問題時不可避免會陷入局部最優,仿真計算出的充電站的收益分布呈現出波動性,對收益分布進行擬合,并以此作為充電站收益分布的參考值來估計充電站的最優容量配置.

圖5 不同儲能容量配置下充電站經濟收益Fig.5 Economic benefits of charging station underdifferent energy storage capacity

充電站收益隨著儲能配置容量的增加總體上呈現出先增后減的趨勢. 因為在初始階段,儲能能夠充分發揮其削峰填谷的作用,儲能容量增加為運營商帶來的收益高于其配置成本,但是隨著儲能配置容量的繼續增加,儲能配置的成本越來越高,儲能所能實現的收益無法覆蓋其配置成本,使得充電站收益呈現下降趨勢. 通過收益分布和擬合的結果可知,充電站儲能容量在580 kWh附近處有最優經濟配置.

4.2.2 對比分析

為體現本文最終優化結果的有效性和優越性,本文引入傳統配置方案進行對比. 方案1為傳統配置方案,該方案是以峰谷差為主要優化目標的儲能配置. 方案2為本文所提方案,是綜合考慮了以充電站負荷以及經濟性為優化目標的儲能配置.

在同等儲能容量配置(580 kWh)的前提下,兩種方案的充電站站內負荷優化結果及儲能充放電功率曲線如圖6、圖7所示. 以01:00—18:00時段為例,可以看到01:00—9:00電價在低谷時段,兩種方案下的儲能系統都處于充電狀態,站內負荷功率抬升. 09:00—13:00電價在高峰時段,方案2下儲能系統處于放電狀態,而方案1由于沒有達到全天負荷功率上限的參考值,儲能處于閑置狀態,僅通過光伏補充一部分用電需求. 13:00—18:00電價處于平時段,此時段站內充電功率較為分散,且有光伏出力,方案1在該時段沒有考慮為儲能充電,導致該時段站內充電功率下陷. 而方案2在該時段處于充電狀態,因此站內負荷功率沒有出現明顯的下陷,提高了電能的利用率. 方案2充分考慮了站內電動汽車負荷特性,制定了合理的運行策略. 按照該策略,儲能系統一天可以做到兩充兩放,儲能利用效率提升了一倍左右,有效利用了平谷時段多余的電量. 結合表2中的3項主要的優化指標可以看出,兩種方案在前兩項指標上較為接近,相比未優化前都有較大提升,在總削峰量上,方案2比方案1提升了48.12%,因此方案2比方案1有更好的負荷優化效果.

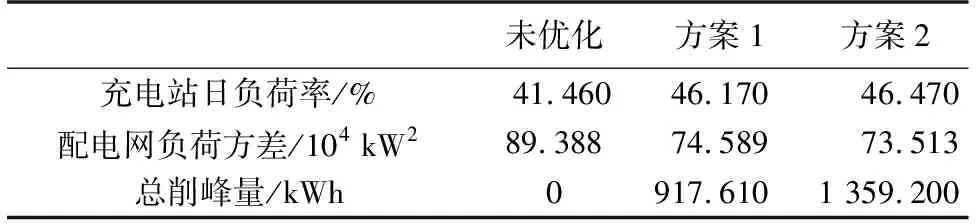
表2 充電站儲能配置前后負荷優化指標Table 2 Load optimization index of charging stationbefore and after energy storage configuration

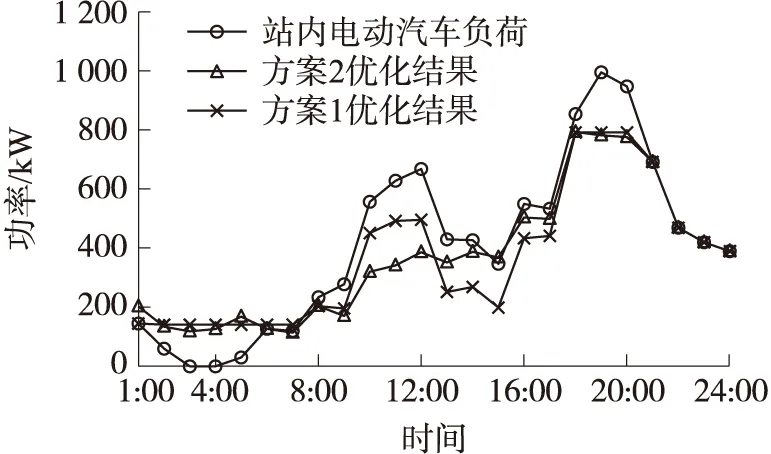
圖6 儲能配置前后站內負荷對比Fig.6 Comparison of station load before andafter energy storage configuration

圖7 儲能充放電功率優化曲線Fig.7 Energy storage charge/dischargeoptimization curve

由表3中給出的經濟性指標可知,方案2由于合理利用峰谷電價來安排儲能的充放電,儲能的利用率要高于方案1. 相應地,儲能的削峰量也高于方案1,所以方案2的年削峰激勵比方案1高出了22 962.6元. 從年購電成本上看,方案2較方案1減少年購電成本3.68萬元,是因為一天中峰值時段的負荷量占到全天總負荷量的61.1%,方案2最大限度地利用平谷時段的低價電,可以減少對峰值時段高價電的依賴性,從而降低充電站的購電成本,進一步提升了充電站整體的經濟效益.

表3 充電站儲能配置前后經濟性指標Table 3 Economic index of charging stationbefore and after energy storage configuration

5 結論

本文研究了商業區光儲充電站儲能經濟性配置問題,考慮到充電站電動汽車負荷優化,制定了峰谷電價場景下的儲能運行策略,建立了儲能配置雙層規劃模型. 通過與傳統以峰谷差為指標的配置方案對比,本文所提方案儲能利用率提升了一倍左右,較好地改善了充電站的負荷分布情況,尤其是充電站總削峰量相比傳統方案提升了48.12%,與此同時充電站的年購電成本減少了3.68萬元,說明本文配置模型的有效性. 因此,在具體工程應用中,為緩解充電站與電網之間的供需矛盾,可為充電站配置一定容量的儲能作為緩沖. 另外,還應該根據充電站的負荷特點為儲能設計合理的調度模型,通過對儲能充放電的控制實現充電站整體經濟性的提升.