一類小世界網(wǎng)絡(luò)的特征值研究

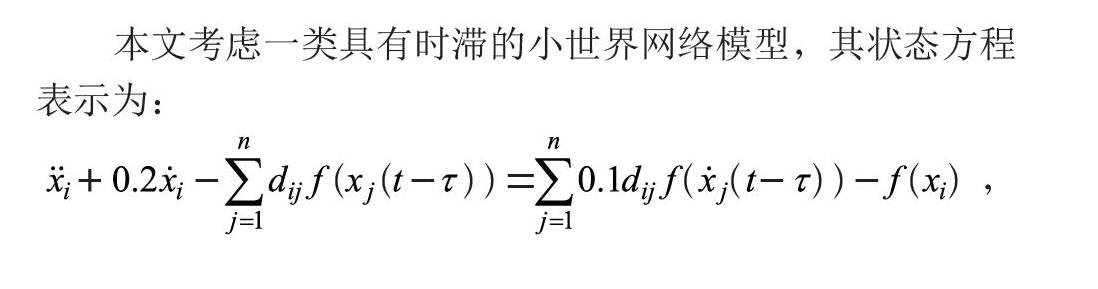
摘? 要：研究了一類具有隨機(jī)長(zhǎng)連接強(qiáng)度的時(shí)滯小世界網(wǎng)絡(luò)的特征值分布。首先給出小世界網(wǎng)絡(luò)的結(jié)構(gòu)和矩陣表示，分析了構(gòu)成小世界網(wǎng)絡(luò)的規(guī)則環(huán)形網(wǎng)絡(luò)的連接強(qiáng)度矩陣的最大特征值、最小特征值和其他n-2個(gè)特征值的取值范圍，討論了小世界網(wǎng)絡(luò)的長(zhǎng)連接強(qiáng)度矩陣元素Xij的數(shù)學(xué)期望和方差，進(jìn)而分析了小世界網(wǎng)絡(luò)的長(zhǎng)連接強(qiáng)度矩陣X的特征值分布，最后給出了小世界網(wǎng)絡(luò)連接強(qiáng)度矩陣D的特征值分布。

關(guān)鍵詞：小世界網(wǎng)絡(luò);隨機(jī)長(zhǎng)連接強(qiáng)度;時(shí)滯;特征值分布

中圖分類號(hào)：O157.5? ? ? 文獻(xiàn)標(biāo)識(shí)碼：A 文章編號(hào)：2096-4706（2021）05-0135-03

Study on the a Kind of Eigenvalues of Small World Network

ZHOU Jing

（Institute of Information Technology，Jilin Agricultural University，Changchun? 130118，China）

Abstract：A kind of eigenvalue distribution of a small world network with time delay with random long connection strength is studied. Firstly，the structure and matrix representation of small world network are given. The maximum eigenvalue，the minimum eigenvalue and the value range of other n-2 eigenvalues of the connection strength matrix of regular ring network of small world network are analyzed. The mathematical expectation and variance of the element Xij of the long connection strength matrix of small world network is discussed，then the eigenvalue distribution of the long connection strength matrix X of small world network is analyzed. Finally，the eigenvalue distribution of the connection strength matrix D of small world network is given.

Keywords：small world network;random long connection strength;time delay;eigenvalue distribution

0? 引? 言

小世界網(wǎng)絡(luò)是一類特殊的復(fù)雜網(wǎng)絡(luò)，具有較高的集聚系數(shù)和較短的平均路徑長(zhǎng)度，它普遍存在于人類社會(huì)中，我們比較熟悉的人際關(guān)系網(wǎng)絡(luò)、交通網(wǎng)絡(luò)、大腦功能網(wǎng)絡(luò)[1]以及最近兩年對(duì)人們的生產(chǎn)生活產(chǎn)生著巨大影響的新冠病毒傳播網(wǎng)絡(luò)[2]等等，這些網(wǎng)絡(luò)都有著明顯的小世界特性。因此，關(guān)于小世界網(wǎng)絡(luò)方面的研究，特別是小世界網(wǎng)絡(luò)的建模、動(dòng)力學(xué)性質(zhì)以及控制等方面的研究得到了全世界專家和學(xué)者們的廣泛關(guān)注，取得了許多有意義的研究成果，并在各個(gè)領(lǐng)域得到了廣泛的應(yīng)用。

小世界網(wǎng)絡(luò)的結(jié)構(gòu)復(fù)雜多樣，因此在以往很多關(guān)于小世界網(wǎng)絡(luò)的研究中，為方便討論，通常假設(shè)網(wǎng)絡(luò)的結(jié)構(gòu)和節(jié)點(diǎn)間的連接方式是固定不變的，網(wǎng)絡(luò)節(jié)點(diǎn)間的連接概率、連接強(qiáng)度及時(shí)滯等網(wǎng)絡(luò)參數(shù)均為常數(shù)。然而，在實(shí)際的復(fù)雜網(wǎng)絡(luò)系統(tǒng)中，系統(tǒng)的內(nèi)部結(jié)構(gòu)和外部的干擾對(duì)小世界網(wǎng)絡(luò)的行為和性能有著非常重要的影響。特別地，對(duì)于小世界網(wǎng)絡(luò)來(lái)說(shuō)，長(zhǎng)連接是小世界網(wǎng)絡(luò)的重要標(biāo)志，起著關(guān)鍵性的作用，因此，如果對(duì)長(zhǎng)連接的連接方式和連接強(qiáng)度的研究更接近于現(xiàn)實(shí)世界中小世界網(wǎng)絡(luò)的長(zhǎng)連接的話，那將更有利于促進(jìn)人們對(duì)復(fù)雜網(wǎng)絡(luò)系統(tǒng)的認(rèn)識(shí)，掌握它的發(fā)展方向和未知的應(yīng)用。

在小世界網(wǎng)絡(luò)的相關(guān)研究中，關(guān)于網(wǎng)絡(luò)動(dòng)力學(xué)行為的研究更加受到研究者們的青睞，如穩(wěn)定性問(wèn)題、分岔問(wèn)題、同步問(wèn)題等等。一般地，為了定量的研究上述諸多問(wèn)題，通常用微分方程或時(shí)滯微分方程來(lái)描述小世界網(wǎng)絡(luò)，而特征值問(wèn)題是研究微分方程動(dòng)力學(xué)性質(zhì)的關(guān)鍵問(wèn)題，學(xué)者們?cè)谶@方面也已經(jīng)取得了大量的研究成果，如：羅佳偉等[3]應(yīng)用特征值法給出了穩(wěn)定性切換準(zhǔn)則，研究了參數(shù)與時(shí)滯相關(guān)的延遲振子的穩(wěn)定性;盛夏等[4]應(yīng)用特征值法分析一個(gè)具有時(shí)滯的高維環(huán)狀神經(jīng)網(wǎng)絡(luò)周期解的線性穩(wěn)定性，給出了從平凡解分岔出周期解的局部存在性;YU等[5]應(yīng)用特征值法討論了一類具有興奮性和抑制性長(zhǎng)連接的時(shí)滯小世界網(wǎng)絡(luò)的穩(wěn)定性、不穩(wěn)定性和分岔模式，給出了穩(wěn)定性的一般條件和數(shù)值模擬的結(jié)果。但是目前對(duì)于具有隨機(jī)連接強(qiáng)度的小世界網(wǎng)絡(luò)模型特征值分布的研究卻較少。本文研究了一類具有時(shí)滯和非線性因素的小世界網(wǎng)絡(luò)，其網(wǎng)絡(luò)節(jié)點(diǎn)間的長(zhǎng)連接是隨機(jī)的，連接強(qiáng)度也是具有某種分布的隨機(jī)變量，在此基礎(chǔ)上來(lái)研究小世界網(wǎng)絡(luò)連接矩陣的特征值問(wèn)題。

1? 小世界網(wǎng)絡(luò)模型

本文考慮一類具有時(shí)滯的小世界網(wǎng)絡(luò)模型，其狀態(tài)方程表示為：

，i=1，2，…，n? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1）

式中，xi（t）為第i個(gè)振子的位移，f（xi）為非線性函數(shù)，滿足f（0）=0，而且f '（0）=1，τ>0為時(shí)滯，dij為網(wǎng)絡(luò)節(jié)點(diǎn)間的連接強(qiáng)度，如果節(jié)點(diǎn)間不存在連接，則dij=0，如果節(jié)點(diǎn)間存在連接，則dij≠0，dij=dji，且連接以彈性力和阻尼力的形式存在。

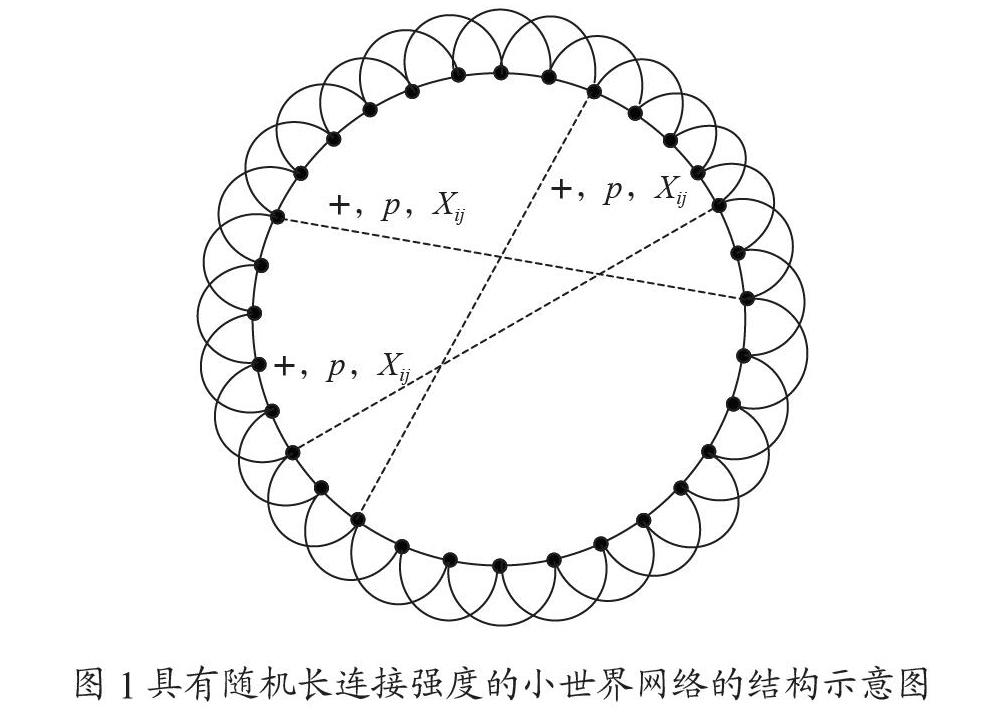
小世界網(wǎng)絡(luò)的結(jié)構(gòu)示意圖如圖1所示，它是一類Newman-Watts小世界網(wǎng)絡(luò)。圖中每個(gè)黑色的圓圈代表一個(gè)節(jié)點(diǎn)，每條直線（包括實(shí)線和虛線）代表兩個(gè)節(jié)點(diǎn)之間的一個(gè)連接。網(wǎng)絡(luò)的具體構(gòu)建方式如下：首先，建立一個(gè)含有n（n充分大）個(gè)節(jié)點(diǎn)的規(guī)則環(huán)形網(wǎng)絡(luò)，每個(gè)節(jié)點(diǎn)都與其左右各2個(gè)節(jié)點(diǎn)相連，每個(gè)節(jié)點(diǎn)都不與自身相連。然后，在規(guī)則環(huán)形網(wǎng)絡(luò)的基礎(chǔ)上，隨機(jī)的選取兩個(gè)節(jié)點(diǎn)用直線連接，并設(shè)此長(zhǎng)連接是一條激勵(lì)的連接，圖中使用“+”來(lái)表示，連接概率設(shè)為p（p?1），這里，我們假設(shè)節(jié)點(diǎn)i與節(jié)點(diǎn)j之間的長(zhǎng)連接強(qiáng)度是服從某一概率分布的隨機(jī)變量，不再是固定的常數(shù)，用Xij來(lái)表示。

2? 小世界網(wǎng)絡(luò)的矩陣表示和特征值分析

將狀態(tài)方程（1）在零平衡點(diǎn)處線性化，可得：

，i=1，2，…，n

（2）

方程（2）整理成矩陣形式為：

（3）

方程（3）中的矩陣x=（x1，x2，…，xn）T表示小世界網(wǎng)絡(luò)節(jié)點(diǎn)的狀態(tài)矩陣，矩陣D=（dij）n×n則表示小世界網(wǎng)絡(luò)的連接強(qiáng)度矩陣。根據(jù)研究需要，我們將連接強(qiáng)度矩陣表示為一個(gè)規(guī)則環(huán)形網(wǎng)絡(luò)的連接強(qiáng)度矩陣V=（vij）n×n與小世界網(wǎng)絡(luò)的長(zhǎng)連接強(qiáng)度矩陣X=（Xij）n×n的和矩陣，由所建小世界網(wǎng)絡(luò)模型的特點(diǎn)，可知矩陣D，V，X均為實(shí)對(duì)稱矩陣。通常，小世界網(wǎng)絡(luò)連接強(qiáng)度矩陣的特征值被稱為網(wǎng)絡(luò)的特征值，下面，我們通過(guò)分析實(shí)對(duì)稱矩陣V與X的特征值分布來(lái)討論小世界網(wǎng)絡(luò)特征值的分布。

引理1[6]：如果矩陣A為n階實(shí)對(duì)稱矩陣，它的每行元素之和都是相等的，則矩陣A的全部特征值均是實(shí)數(shù)，且A的最大特征值等于它的每行元素相加的和，A的最小特征值可以表示為，其中，m和k分別為規(guī)則環(huán)形網(wǎng)絡(luò)節(jié)點(diǎn)的度和連接強(qiáng)度。

本文中，我們?cè)O(shè)規(guī)則環(huán)形網(wǎng)絡(luò)節(jié)點(diǎn)的度為4，節(jié)點(diǎn)間的連接強(qiáng)度為0.01，即當(dāng)j∈[i-2，i+2]，（i，j=1，2，…，n）

時(shí)，vij=0.01，在i，j取其他值的情況下，vij=0，則根據(jù)引理1，可以給出規(guī)則環(huán)形網(wǎng)絡(luò)的連接強(qiáng)度矩陣V的特征值分布。

結(jié)論1：設(shè)α1>α2>…>αn為規(guī)則環(huán)形網(wǎng)絡(luò)連接強(qiáng)度V的n個(gè)特征值，則V的最大特征值為α1=4×0.01=0.04，最小特征值為 ，其他n-2個(gè)特征值介于最大和最小特征值之間。

一般的，對(duì)于真實(shí)的網(wǎng)絡(luò)系統(tǒng)，網(wǎng)絡(luò)的節(jié)點(diǎn)數(shù)目n較大，而長(zhǎng)連接概率p較小，文獻(xiàn)[7]針對(duì)這種網(wǎng)絡(luò)進(jìn)行了相應(yīng)的討論，可以將小世界網(wǎng)絡(luò)的長(zhǎng)連接強(qiáng)度矩陣X=（Xij）n×n近似的看作是一個(gè)完全隨機(jī)的實(shí)對(duì)稱矩陣，當(dāng)j∈[i-2，i+2]，（i，j=1，2，…，n）時(shí)，Xij=0，在i，j取其他值的情況下，兩節(jié)點(diǎn)之間以概率p進(jìn)行連接，如果存在長(zhǎng)連接（已假設(shè)是激勵(lì)的長(zhǎng)連接），則連接強(qiáng)度Xij=Wij=Wji為服從某種分布的隨機(jī)變量，不再是固定的常數(shù)，否則Xij=0。我們?cè)O(shè)Wij的均值為μ>0，即E（Wij）=μ，方差為σ2，即Var（Wij）=σ2，也就是說(shuō)隨機(jī)變量Xij的概率分布為P（Xij=μ）=p，P（Xij=0）=1-p。已知，當(dāng)i與j以概率p連接時(shí)，有Xij=Wij，根據(jù)隨機(jī)變量期望的性質(zhì)，，所以，隨機(jī)變量的概率分布為 。需要注意的是，在長(zhǎng)連接矩陣中，連接概率分布和連接強(qiáng)度分布是相互獨(dú)立的，因此長(zhǎng)連接矩陣X的所有元素都是相互獨(dú)立的隨機(jī)變量，由概率論相關(guān)方面的知識(shí)，可得連接強(qiáng)度Xij的期望為：

E（Xij）=pμ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）

方差為：

（5）

結(jié)論2：當(dāng)網(wǎng)絡(luò)的節(jié)點(diǎn)數(shù)目n較大，而長(zhǎng)連接概率p較小時(shí)，小世界網(wǎng)絡(luò)的長(zhǎng)連接強(qiáng)度Xij的期望為pμ，方差為p（σ2+μ2）-p2μ2，其中μ和σ2分別為節(jié)點(diǎn)間存在長(zhǎng)連接時(shí)的連接強(qiáng)度的均值和方差。

引理2[8]：設(shè)A=（aij）n×n是實(shí)對(duì)稱隨機(jī)矩陣，即當(dāng)i≥j時(shí)，元素aij都是相互獨(dú)立的隨機(jī)變量，且E（aii）= v，E（aij）=μ，Var（aij）=σ2。如果μ>0，設(shè)ε1>ε2>…>εn為矩陣A的n個(gè)特征值，則最大特征值ε1近似的服從正態(tài)分布，它的期望和方差分別為：

E（ε1）=（n-1）μ+v+σ2/μ，Var（ε1）=2σ2? ? ? （6）

其他n-1個(gè)特征值滿足 的概率等于1。

根據(jù)引理2和式（4）～（5），我們可以給出小世界網(wǎng)絡(luò)長(zhǎng)連接強(qiáng)度矩陣X的特征值的分布，如結(jié)論3所述。

結(jié)論3：如果小世界網(wǎng)絡(luò)的節(jié)點(diǎn)數(shù)目n充分大，且長(zhǎng)連接概率p足夠小，則長(zhǎng)連接矩陣可以近似為一個(gè)完全隨機(jī)矩陣。設(shè)β1>β2>…>βn為網(wǎng)絡(luò)長(zhǎng)連接強(qiáng)度X的特征值，則最大特征值β1近似的服從正態(tài)分布，它的期望和方差分別為：

E（β1）=（n-6）pμ+σ2/μ+μ，Var（β1）=2[p（σ2+μ2）-p2μ2]

（7）

其他n-1個(gè)特征值滿足? ?的概率等于1。

引理3（矩陣擾動(dòng)理論[9]）：設(shè)實(shí)對(duì)稱矩陣A，B，C滿足B=A+C，且矩陣A，B，C的特征值分別滿足式（8）給出的不等式關(guān)系：

α1>…>αn;β1>…>βn;γ1>…>γn? ? ? ? ?（8）

則矩陣B的特征值滿足式（9）給出的不等式：

ai+εn≤βi≤ai+ε1，i=1，2，…，n? ? ? ? ? ? ?（9）

根據(jù)結(jié)論3和引理3，我們可以給出小世界網(wǎng)絡(luò)連接強(qiáng)度矩陣D的特征值的分布，如結(jié)論4所述。

結(jié)論4：設(shè)γ1>γ2>…>γn是小世界網(wǎng)絡(luò)連接強(qiáng)度矩陣D的n個(gè)單特征值，則D的最大特征值滿足不等式γ1≤ α1+β1，最小特征值滿足式（10）：

（10）

其他n-2個(gè)特征值介于最大和最小特征值之間。

3? 結(jié)? 論

綜上，本文研究了一類具有隨機(jī)長(zhǎng)連接強(qiáng)度的時(shí)滯小世界網(wǎng)絡(luò)模型的特征值分布。首先我們給出了小世界網(wǎng)絡(luò)的結(jié)構(gòu)示意圖，它是以規(guī)則環(huán)形網(wǎng)絡(luò)為基礎(chǔ)得到的一類Newman-Watts小世界網(wǎng)絡(luò)。通過(guò)分析得到了規(guī)則環(huán)形網(wǎng)絡(luò)的連接強(qiáng)度矩陣的特征值分布，討論了當(dāng)網(wǎng)絡(luò)的節(jié)點(diǎn)間以概率p（p?1）進(jìn)行長(zhǎng)連接，且長(zhǎng)連接強(qiáng)度為服從某一分布的隨機(jī)變量時(shí)，小世界網(wǎng)絡(luò)的長(zhǎng)連接強(qiáng)度矩陣元素Xij的期望和方差，并給出了此時(shí)長(zhǎng)連接強(qiáng)度矩陣X的特征值分布，最后給出小世界網(wǎng)絡(luò)連接強(qiáng)度矩陣D的最大和最小特征值的取值范圍和其他n-2個(gè)特征值分布。通過(guò)以上研究，有利于深入了解真實(shí)小世界網(wǎng)絡(luò)的結(jié)構(gòu)和性能，能夠?yàn)榻窈罄^續(xù)探索小世界網(wǎng)絡(luò)的動(dòng)力學(xué)行為和性質(zhì)奠定良好的基礎(chǔ)。

參考文獻(xiàn)：

[1] 王祖力，張艷.腦功能網(wǎng)絡(luò)核心節(jié)點(diǎn)及網(wǎng)絡(luò)穩(wěn)定性研究 [J].中國(guó)計(jì)量學(xué)院學(xué)報(bào)，2014，25（4）：414-418.

[2] 陸君安，王沛.從復(fù)雜網(wǎng)絡(luò)小世界、無(wú)標(biāo)度、高聚類特性看新型冠狀病毒肺炎 [EB/OL].（2020-02-06）.https：//www. 163.com/dy/article/F4O4UQHB0511D05M.html.

[3] 羅佳偉，徐旭.參數(shù)與時(shí)滯相關(guān)延遲振子的穩(wěn)定性及Hopf分岔分析 [J].吉林大學(xué)學(xué)報(bào)（理學(xué)版），2018，56（6）：1337-1344.

[4] 盛夏，張麗，鄭虹，等.具有時(shí)滯的高維網(wǎng)絡(luò)系統(tǒng)的周期解 [J].吉林大學(xué)學(xué)報(bào)（理學(xué)版），2010，48（5）：728-732.

[5] YU D Y，XU X，ZHOU J，et al. Stability and instability of a neuron network with excitatory and inhibitory small-world connections [J].Neural Networks，2017，89：50-60.

[6] ZHOU J，XU X，YU D Y，et al. Stability，Instability and Bifurcation Modes of a Delayed Small World Network with Excitatory or Inhibitory Short-Cuts [J/OL].International Journal of Bifurcation and Chaos，2016，26（4）：[2021-01-06].https：//www.worldscientific.com/doi/abs/10.1142/S021812741650070X.

[7] GRAY R M. Toeplitz and Circulant Matrices：A Review [J].Foundations and Trends? in Communications and Information Theory，2006，2（3）：155-239.

[8] F?REDI Z，KOML?S J. The eigenvalues of random symmetric matrices [J].Combinatorica，1981（1）：233-241.

[9] 孫繼廣.矩陣擾動(dòng)分析：第2版 [M].北京：科學(xué)出版社，2001.

作者簡(jiǎn)介：周晶（1980—），女，漢族，吉林德惠人，講師，博士，研究方向：復(fù)雜網(wǎng)絡(luò)的動(dòng)力學(xué)與控制。