基于設計地震動的斜入射波時程確定方法對土石壩地震響應的影響

王 飛, 宋志強, 劉云賀, 張劍峰

(1.西安理工大學 省部共建西北旱區生態水利國家重點實驗室,西安 710048； 2.中國三峽建設管理有限公司,成都 610041)

地震動輸入是大壩抗震設計計算的前提，入射波是地震動輸入的基礎。GB 51247—2018 《水工建筑物抗震設計標準》[1]規定采用平坦基巖地表水平向地震動峰值加速度作為表征設計地震動強度的主要參數，設計地震動是抗震計算的依據，因此，研究設計地震動下入射波幅值及時程確定方法具有重要實際工程意義。在進行大壩抗震設計計算時，通常假定地震波垂直入射[2]，按一維反演方法依據壩址設計地震動水平分量確定入射波幅值和時程。然而，當工程場地距震源較近時，地震波經過有限次反射和透射后到達地表，并不滿足垂直入射假定[3-5]。因此，有必要研究地震波斜入射時基于水平和豎直兩向設計地震動的入射波幅值和時程確定方法。

進行地震波斜入射下結構地震響應分析時，很難確定地基底部地震波時間序列，通常仍然按照垂直入射的方法，直接把實測地震動記錄或者人工合成地震動水平分量當作入射波，再或者進行1/2倍調幅，把調幅后的地震動作為入射地震波。張樹茂等[6]將場地譜地震動時程作為地基底部入射波，研究了P波和SV波斜入射下土石壩加速度反應隨入射角的變化規律。王飛等[7]以實測近斷層地震動記錄作為基巖地基底部的斜入射波，研究了近斷層地震動斜輸入作用下水電站廠房的非線性地震響應。孫緯宇等[8]以EI-Centro波、Northridge波和寧河波作為入射波，研究了P波和SV波斜入射下河谷場地地震動放大系數隨入射角的分布特征。Sun等[9]和李明超等[10]將平坦基巖地表水平向設計地震動按1/2倍調幅，以調幅后的地震動作為基巖地基底部的入射波，分別研究了地下水工隧洞和重力壩的非線性地震響應隨地震波入射角度的變化規律。單純分析地震波斜入射下結構的地震響應時，上述入射波時程確定方法是能夠接受的，但上述方法在任意角度下入射波幅值和時程是不變的，沒有考慮斜入射波時程與入射角度的內在聯系，造成地表水平地震動峰值隨入射角變化而變化[11]，獲得的結構地震響應隨入射角變化的規律包含了地震動強度變化的貢獻，導致結構的地震響應并不是設計地震動作用下的結果。

本文在P波和SV波組合斜入射前提下，考慮兩者對半無限空間自由場的共同貢獻，基于波場疊加原理，構建了均質基巖二維空間自由場，根據控制點自由場運動分量與設計地震動對應分量相同的原則，建立入射波時程與入射角度的函數關系，提出了基于設計地震動的入射波時程確定方法。分析了按垂直入射假定確定斜入射波時程時半無限空間地表自由場和基巖-覆蓋層-土石壩系統地震響應相對于本文方法的偏差。應用本文方法分析了斜入射引起的地表非一致運動，研究了相同設計地震動條件下，不同斜入射角對土石壩的非一致地震響應影響規律。

1 基于設計地震動的斜入射波時程確定方法

1.1 方法1

通常情況下，基巖平坦地表地震動假定由垂直地表的入射波和同相位等幅值的反射波疊加組成，該假定對于距震源較遠場地上的地震動是合理的，此時，基巖地基底部入射波可按平坦自由地表水平向設計地震動1/2調幅獲得，稱為方法1。

當P波或SV波入射角為0°時，平坦地表自由場地震動幅值和波形與設計地震動吻合。但當震源距離壩址較近時，入射波傳播方向與水平地表并非垂直，而是與水平地表的法向存在不確定性夾角。當研究基于設計地震動的斜入射地震波對結構地震響應的影響時，仍按方法1確定斜入射波時程，由于不考慮斜入射波時程隨入射角度的變化而變化，因此隨著入射角增大，平坦地表地震動幅值和波形將逐漸偏離設計地震動：根據王飛[12]的研究結論，當平面P波斜入射時，平坦地表水平向地震動強度隨入射角增大先增大后減小，豎向地震動強度隨入射角增大而減小；當平面SV波斜入射時，水平向地震動強度隨入射角增大而增大，豎向地震動強度隨入射角增大先增大后減小。

1.2 方法2

近地表入射地震波成分復雜，基巖平坦地表設計地震動不能假定僅由某一類型體波組成。而應該考慮兩種體波的共同作用。平面P波和SV波斜入射至自由地表均會產生反射P波和SV波，如圖1所示。虛線箭頭表示地震波的傳播方向，實線箭頭表示質點振動方向。坐標原點O為控制點，設計地震動水平分量為ux(t)，豎向分量為uy(t)。入射P波位移波函數為g(t)，振動矢量m(0)=(sinα, cosα)，入射SV波位移波函數為f(t)，振動矢量n(0)=(cosγ,-sinγ)。半無限均質彈性空間任意點自由場由兩種體波(P波和SV波)的入射波場、反射波場共同疊加組成[13]

(a) P波斜入射

水平向

(1)

豎向

(2)

式中：cP和cS分別為P波和SV波波速；A1，A2為P波斜入射下反射P波和反射SV波幅值與入射P波幅值的比值;B1,B2為SV波斜入射下反射SV波和反射P波幅值與入射SV波幅值的比值，分別如下

(5)

式中,E,ρ和μ分別為介質的彈性模量、密度和泊松比。

在水平自由地表，y為一常數且等于零，結合Snell定律，水平自由地表任意點自由場可表示為

水平向

(7)

假設水平自由地表任意點的運動在整個時間歷程中由入射P波和SV波共同作用，即P波和SV波同時傳播至水平自由地表，則有式(8)成立

(8)

取任意點為控制點O(x=0,y=0)，則需要滿足的條件是該點的自由場水平向和豎向分量與設計地震動對應的兩向分量相同，根據式(6)和式(7)，可得到兩個方程

水平向

ag(t)+bf(t)=ux(t)

(9)

豎向

cg(t)-df(t)=uy(t)

(10)

式中:a=(sinα+A1sinα-A2cosβ);b=(cosγ-B1cosγ+B2sinθ);c=(cosα-A1cosα-A2sinβ);d=(sinγ-B1sinγ-B2cosθ)。當設計地震動兩分量和半無限空間介質信息已知時，聯立式(9)和式(10)，可以建立P波和SV波時程關于入射角的函數關系式，進而可由入射角推求組合入射波時程。為方便起見，將本文建立的考慮斜入射P波和SV波對設計地震動的組合貢獻、根據入射角度確定入射波時程的方法稱為方法2。

2 不同斜入射波時程確定方法對均質半無限空間自由場響應的影響

從平面半無限均質空間截取長度為400 m(2L)、深度為200 m(H)的有限域地基，如圖2所示。地基彈性模量為1.3 GPa，密度為2 000 kg/m3，泊松比為0.25。P波波速為883 m/s，SV波波速為510 m/s。地表控制點O設計地震動水平和豎向位移時程均如式(11)所示，位移波形如圖3所示。位移峰值為2.60 m。基于設計地震動時程，按照方法1確定P波或SV波單波斜入射時程，按照方法2確定與入射角度相關的P波和SV波組合斜入射時程。假定單波或組合波均從地基左側斜向上入射，分析不同斜入射波時程確定方法對O點自由場響應的影響。

圖2 半無限均質彈性空間計算模型(m)

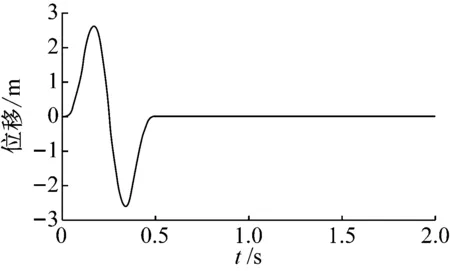
圖3 水平向和豎向設計地震動時程

(11)

方法1和方法2均是先給定P波斜入射角，然后按照式(8)確定SV波斜入射角，表1給出了不同入射角度下入射波位移峰值、地表O點水平和豎向位移峰值及其相對設計地震動峰值的誤差。表1表明，方法1任意入射角度下，入射P波或SV波位移峰值均是設計地震動水平向峰值的1/2，即為1.30 m。方法2中入射P波位移峰值隨入射角度增大而增大，入射SV波位移峰值隨入射角增大而減小。不管何種入射角下，方法2中O點水平和豎向位移峰值均與設計地震動吻合，而在相同入射角下，方法1獲得的地表O點自由場響應與設計地震動差異顯著：其中當P波入射角為45°時，O點水平向和豎向位移峰值分別比設計地震動減小了23.85%和31.63%，當SV波入射角為24.1°時，O點水平向和豎向位移峰值分別比設計地震動減小了2.31%和62.69%。

表1 不同入射波時程確定方法下O點位移峰值及其相對設計地震動誤差

圖4和圖5分別給出了不同入射角下地表O點水平向和豎向位移時程曲線，由圖4和圖5可知:方法2中P波、SV波組合入射前提下，不論何種入射角度組合，地表點O水平向和豎向位移波形與設計地震動完全吻合，該斜入射波時程確定方法能夠反映設計地震動作用下半無限空間自由場響應。方法1中，當P波斜入射或者SV波斜入射時，點O位移波形均與設計地震動有較大差異。

(a) P波0°，SV波0°

(a) P波0°，SV波0°

圖6和圖7分別給出了兩種方法獲得的P波入射角為45°、SV波入射角為24.1°時地表O點和左上角A點、右上角B點的水平向和豎向位移時程曲線。由圖6和圖7可知:地震波斜入射引起地表空間點發生非一致運動，任意兩點開始振動的時間間隔隨入射角的增大而增大。方法1表現的非一致運動峰值與設計地震動峰值有較大的誤差，方法2表現的非一致運動波形和峰值均與設計地震動吻合，方法2能夠反映設計地震動下的地表非一致運動。

(a) 方法1中P波斜入射

(a) 方法1中P波斜入射

當斜入射波幅值取設計地震動幅值的1/2且只包含一種體波(P波、SV波)時，地表自由場運動與設計地震動誤差較大，難以反映設計地震動下的斜入射波作用下結構的地震響應。考慮P波和SV波對半無限空間自由場的共同作用，按入射角確定入射P波和SV波時程，獲得的地表自由場運動與設計地震動吻合，并且各點地震動呈現出明顯的非一致性，能夠合理反映設計地震動下的斜入射波作用下結構的非一致地震響應。

3 不同斜入射波時程確定方法對土石壩地震響應影響

3.1 計算模型

以坐落在覆蓋層地基上的均質土石壩為研究對象，壩高100 m，壩頂寬10 m，上游、下游壩坡均為1∶1.6，覆蓋層深度為100 m，基巖地基底部取至地表以下200 m處，基巖-覆蓋層-土石壩系統，如圖8所示。采用鄧肯-張E-B模型[14]描述壩料和覆蓋層的靜力非線性彈性行為。動力時程計算采用等效線性方法，壩料和覆蓋層土體采用沈珠江等[15]建議的修正等效黏彈性模型，動力計算參數,如表2所示。表2中k1，k2和n均為土石料動三軸試驗參數，λmax為最大阻尼比，μ為泊松比。基巖彈性模量、密度和泊松比分別為8 GPa，2 750 kg/m3和0.24。

圖8 基巖-覆蓋層-土石壩系統計算模型(m)

表2 動力計算參數

以Imperial Valley-02地震(1940年，美國)中EI-Centro Array#9臺站記錄到的實測地震動作為平坦基巖表面上的設計地震動，設計地震動水平向和豎向位移分量，如圖9所示。

(a) 水平向

3.2 二維基巖-覆蓋層地基斜入射輸入方法

通常，一般工程根據GB 18306—2015《中國地震動參數區劃圖》[16]確定設計地震動峰值加速度和場地特征周期，然后人工合成設計地震動。對于設防類別為甲類的重大工程，根據地震部門給出的場址危險性分析結果確定其設計地震動。這兩種方法獲得的設計地震動均是指工程場地所在地區半無限空間均質巖體在平坦地表的地震動，為此，本文選取不受河谷地形影響的平坦基巖表面C點作為控制點，在C點所在的順河向半無限基巖平面(平面1)內，利用本文所建立的方法(方法2)獲得基巖地基底部入射波時程，然后將順河向基巖平面空間(平面1)地基底部的斜入射波時程平移轉換至基巖-覆蓋層地基底部(平面2)，如圖10所示。地震波入射方向與水流向是平行的，只產生平面內運動，在入射方向上不存在河谷地形散射效應。

圖10 基巖-覆蓋層地基底部入射波時程獲取方法示意圖

基巖地基底部及上、下游側采用黏彈性人工邊界[17-21]結合等效結點荷載的地震波動輸入。覆蓋層土體在地震作用下具有明顯的非線性特性[22]，無法通過解析方法獲得覆蓋層上、下游側截斷邊界上的邊界參數和等效結點荷載。為此，地基上、下游采用遠域邊界模擬輻射阻尼效應，遠域地基的截取范圍根據樓夢麟等[23-24]的研究結論，取地基深度的7倍，已經可以滿足工程精度要求。

3.3 土石壩加速度反應

土石壩加速度的計算方案與前面自由場計算的方案一致，其中方法1包括P波斜入射和SV波斜入射兩種情況。圖11為兩種方法獲得的壩頂最大加速度以及方法1相對方法2的偏差。從圖11可知，方法1 P波斜入射情況獲得的壩頂水平向和豎向最大加速度與方法2有較大的差異，相對于方法2水平向和豎向加速度最大偏差分別為90.0%和53.0%，相對偏差均隨入射角增大而減小。方法1 SV波斜入射情況計算得到的壩頂豎向最大加速度相對方法2偏差較大，最大偏差超過了70%，相對偏差隨著入射角度增大先減小后增大；壩頂水平向最大加速度與方法2相近，原因是方法1中地表水平向地震動強度隨角度變化小，與設計地震動水平分量接近。

(a) 水平向

從圖11可知，方法2壩頂水平向和豎向最大加速度隨入射角的增大而減小，原因從圖12(建基面典型點位移時程，點1112和點2601分別位于上、下游壩角，點64位于壩軸線底部)可以得到解釋，與垂直入射相比，地震波斜入射建基面任意兩點地震動初至時間間隔增大，造成各點地面運動存在相位差(圖12中15～20 s的放大位移時程)，地面運動呈現非一致性，減弱了壩體的同頻共振。在位移峰值上，建基面典型點水平向位移峰值最大差異為12.5%，豎向位移峰值最大差異為25.0%。方法1由于控制點已經偏離了設計地震動峰值，所以其難以正確構建非一致地面運動，獲得的壩頂加速度大小隨角度變化的規律中包含著地震動幅值變化的貢獻，無法分析基于設計地震動的入射角變化或者非一致地面運動對壩體響應的影響。

(a) 水平向

由此可見，在任意非垂直入射角度下，基巖地基底部斜入射波幅值取平坦地表水平向設計地震動幅值的一半得到的壩體地震響應不是設計地震動強度下的結果，并且與設計地震動下的計算結果偏差較大。考慮P波和SV波對壩址場地自由場的共同貢獻，根據入射角確定斜入射波時程，可以獲得的壩體非一致地震響應，能夠在相同的設計地震動強度作用下，單純分析入射角對壩體地震響應的影響規律。

圖13和圖14分別為方法2中土石壩1-1剖面和2-2剖面最大加速度分布。1-1剖面和2-2剖面的位置示意,如圖8所示。從圖13可知，土石壩1-1剖面水平向和豎向最大加速度隨入射角的增大而減小，與0°入射角相比，當入射角為45°時水平向和豎向最大加速度減小幅度可達20.8%和31.1%。減小的原因是地震波斜入射引起建基面各點地震動出現相位差，減弱了覆蓋層-土石壩系統的同頻共振，入射角越大，相位差越大，地震動非一致性越顯著。水平向和豎向最大加速度隨高度的增加先減小后增大，在建基面附近，加速度最小，主要是覆蓋層土體進入強非線性狀態，阻尼耗散能力增強，強震作用下覆蓋層對地震波有抑制作用。

(a) 水平向

圖14表明，土石壩2-2剖面(建基面)水平向和豎向最大加速度隨入射角的增大而減小，與0°入射角相比，當入射角為45°時水平向和豎向最大加速度最大減小幅度分別為27.8%和25.9%。由于上游靜水壓力的作用，覆蓋層-土石壩系統上游側震前圍壓大于下游側，導致建基面上游側水平向加速度小于下游側，隨著入射角度增大，上下游側加速度差距更明顯，最小加速度位置逐漸向壩中心移動。上游靜水壓力對豎向加速度的分布規律影響較小，建基面上豎向加速度關于壩體中心對稱分布，壩中心位置豎向加速度最小。

(a) 水平向

4 結 論

本文分析了當前基巖地基底部斜入射波時程的確定方法和適用性，基于設計地震動建立了P波和SV波組合斜入射時程相對于入射角度的函數關系式，實現了入射波時程隨入射角變化，研究了不同斜入射波時程確定方法對半無限均質空間自由場和基巖-覆蓋層-土石壩系統地震響應的影響。結論如下：

(1) 考慮P波和SV波對半無限空間自由場的共同作用，利用入射P波和SV波時程表示了空間任意點自由場，根據控制點自由場分量與設計地震動對應分量相同的原則，建立了斜入射波時程相對于入射角的函數關系式，確定了隨入射角變化的入射波時程。研究了斜入射波幅值取設計地震動幅值的1/2和本文方法下的半無限空間自由表面的位移響應，斜入射波幅值取設計地震動幅值的1/2時，地表位移峰值相對設計地震動有較大誤差，該方法不能應用于確定設計地震動強度下的斜入射波時程。本文方法獲得的地表位移響應與設計地震動吻合，驗證了本文方法的合理性。

(2) 在任意非垂直入射角度下，基巖地基底部入射波幅值取設計地震動幅值的1/2，獲得的土石壩地震響應不是設計地震動強度下的結果，壩頂加速度大小隨角度變化的規律中包含著地震動強度變化的貢獻，與設計地震動強度下的計算結果有較大偏差，無法分析基于設計地震動的入射角變化或者非一致地面運動對壩體響應的影響。

(3) 本文提出的根據入射角確定斜入射波時程的方法，考慮了P波和SV波對壩址場地自由場的共同貢獻，能夠在相同的設計地震動強度作用下，正確反映斜入射角度引起的建基面的非一致運動，可以單純分析斜入射角度對土石壩地震響應的影響。分析結果表明，土石壩加速度反應隨入射角的增大而減小，主要原因是入射角增大，建基面振動方向相位差增大，各位置點運動呈現出非一致現象，減弱了壩體同頻共振的趨勢。