長寧頁巖氣寧納線大落差管段清管沖擊應力與位移分析

彭 陽 安建川 羅 敏 余 進 馬學峰 楊 紅 別 沁 劉 穎 梁 力

1.中國石油西南油氣田公司輸氣管理處 2.中國石油西南油氣田公司

0 引言

長寧—威遠國家級頁巖氣示范區長寧頁巖氣外輸干線寧納線（寧209井區中心站—納溪西站）管道外徑為813 mm，設計壓力為6.3 MPa，設計輸氣量為1 200×104m3/d，線路總長為110.4 km，為中國石油天然氣股份有限公司目前距離最長、管徑最大的頁巖氣外輸管道，于2017年12月投運。該管線沿途翻越多處高陡坡地段，其中垂直落差距離超過200 m的大落差管段共有6處。受起伏地形影響，清管器運行速度會不斷發生改變，尤其是在大落差管段，會加速沖擊管道底部彎頭，使得管道所受最大沖擊應力可能超過許用值而增加失效風險。因此，為了確保后期清管作業的安全，并為清管方案制訂、清管器選型以及清管過程監控等提供依據，有必要對寧納線大落差管段清管沖擊過程進行研究。

現行的標準、規范等側重于清管作業方案制訂、清管器選型、清管安全措施及應急預案實施等[1-3]，對天然氣管道的具體清管技術要求較為簡略。目前針對大落差天然氣管段清管沖擊過程的相關研究工作亦開展得不夠，主要有：喻軍等[4]考慮了管道內壓、清管器速度、土壤類型，利用有限元法研究了中緬天然氣管道某大落差管段受清管器沖擊作用時產生的應力集中及變形問題。李長俊等[5]以云南中緬某大落差管道為研究對象，分析了清管作業時管道內壓、積液量、清管器速度和持液率對沖擊應力的影響。陳利瓊等[6]研究了天然氣管道穿越滑坡地段的應力變化規律。賈彥杰等[7]通過分析獲得了大落差管道清管器的運行規律。劉嘯奔等[8]采用非線性有限元方法，建立了載荷作用下埋地管道彎頭的受力模型，研究了彎頭曲率半徑、彎頭夾角、管土摩擦因數與土壤彈性模量等對管道應力變化的影響。曾鳴等[9]以“川氣東送”大落差天然氣管道為研究對象，分析了橡膠清管球運行速度、內壓對清管沖擊過程管道應力的影響。陳福林等[10]研究了山區輸氣管道清管時，高程差引起的重力位能變化對水力計算以及積水對清管速度的影響。劉浠堯[11]針對中緬天然氣兩段典型大落差管道，研究了不同工況下清管沖擊應力與應變。Zhu等[12-13]對清管過程中雙向直板清管器與管壁的接觸應力參數進行了仿真計算，并比較了線性方法與非線性方法在接觸應力計算中的差異性。Zhang等[14]分析了清管器通過環形焊縫時三個階段的皮碗受力情況。李偉等[15]利用ANSYS/LS-DYNA軟件建立了海底懸空管道受墜物撞擊的三維非線性有限元模型，研究了接觸、摩擦和管—土耦合作用對撞擊動態響應過程的影響。鄧濤等[16]研究了大落差輸氣管道水試壓后清管的壓力脈沖。王文明等[17]采用有限元法研究了清管器對隧道管段的沖擊作用，分析了清管器速度、管道內壓對管道應力與加速度的影響。丁俊剛等[18]從清管方式、清管器速度和清管安全措施等角度，對比了中國和俄羅斯管道清管技術標準的差異。

綜上所述，現階段對大落差天然氣管段清管沖擊過程主要影響因素的考慮不夠全面，因而不能夠充分地了解不同因素對清管器沖擊過程的作用規律，并且沒有對大落差地段天然氣管道敷設時的安全清管極限高度進行研究。為此，以長寧頁巖氣寧納線某大落差管段為研究對象，首先分析了不同因素對清管沖擊過程的影響；其次基于SPT OLGA軟件與ANSYS/LS-DYNA軟件，建立了清管仿真模型，計算出清管速度、管道底部彎頭所受最大沖擊應力及位移；最后，分析得出了大落差管段安全清管條件的計算方法。

1 大落差管道清管過程有限元模型建立與計算

1.1 清管過程仿真幾何模型建立

在實際埋地管道清管過程中，管道、清管器與周圍土壤三者之間相互耦合，因此，對整個體系進行計算較為復雜。為了便于仿真幾何模型建立及提高運算效率，使用了以下假設與簡化：

1）大落差管道所處坡面形狀為若干折線組成的坡面，管道為直管段不存在彎曲。

2）忽略管道外部防腐層影響。

3）不考慮管內氣體對清管器的阻力及升力，清管器只受重力和前后壓差。

4）高差主要影響清管器到達底部彎頭的速度，故取彎頭前端較短長度的管段進行有限元計算。

5）將實際清管器結構進行等質量簡化，并將皮碗的密封盤進行等接觸面積的集中布置。

以表1中的清管器、管道與土壤的相關參數取值為例，建立起大落差管段有限元模型，如圖1所示。

表1 有限元模型建立相關參數取值表

1.2 仿真計算關鍵參數設置與確定

受清管載荷作用，清管器與管道相互接觸。ANSYS軟件在計算清管過程時，兩個模型的接觸力相互傳遞，同時，也在不斷判斷兩個表面是否發生接觸，并不斷修正相應約束條件。目標面和接觸面的選擇依據是將剛度較大的面作為目標面，相應的參數設置見如表2所示。

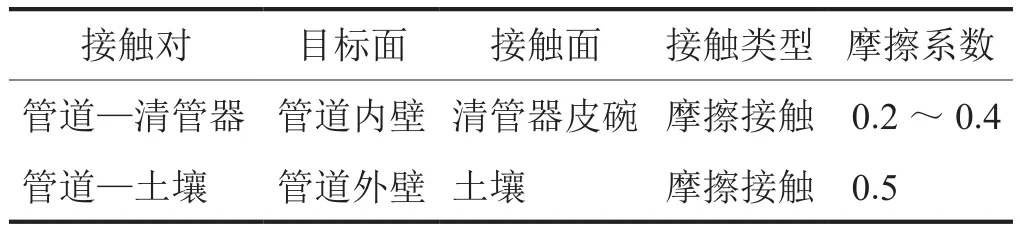
表2 ANSYS軟件仿真過程接觸條件參數設置表

在進行有限元計算時，需要對所設置的單元賦予材料屬性，即選擇本構關系。各部分的材料屬性選擇如下：

1）管道本構關系采用了經典的Ramberg-Osgood模型，ANSYS軟件中管道模型參數設置如表3所示。

表3 ANSYS軟件中管道模型參數設置表

2）清管器本構模型采用Mooney-Rivlin準則。清管器的中部軸承由結構鋼構成，其參數與管材一致。

3）外圈皮碗由可以承受大應變和大變形，但體積改變極微（不可壓縮）的聚氨酯構成，因此，選用能夠準確描述變形范圍為150%以內橡膠材料力學行為的Mooney-Rivlin準則。ANSYS軟件中清管器模型材料參數設置如表4所示。

表4 ANSYS軟件中清管器模型聚氨酯材料參數設置表

4）土壤本構模型采用的是D-P模型。由于研究的大落差管段所處土壤介質主要為黏土，因此，采用了能夠模擬埋地管道周圍土壤在清管器沖擊作用下力學行為的D-P模型來定義土體介質屬性。ANSYS軟件中土壤模型參數設置如表5所示。

表5 ANSYS軟件中黏土土壤模型參數設置表

在有限元計算中，盡量選擇網格質量較高、迭代速度較快的六面體網格，并進行網格無關性驗證。以輸送壓力為4.0 MPa、清管器運行初速度為15 m/s的清管工況為例，通過調整網格尺寸大小對總網格進行控制，選取了 23×104、28×104、33×104、37×104、42×104共5種網格數進行清管沖擊過程仿真計算，管道最大應力變化趨勢如圖2所示。

從圖2可以看出，當網格數量超過33×104個時，最大應力保持在203 MPa左右，由此可確定出模型最優網格數為33×104個左右（實際為339 017）。后續對所有清管工況中應力與位移的有限元計算，均采用上述同樣的方式進行網格無關性驗證，但因計算的工況數量較多，故不再一一贅述。

2 大落差管道清管沖擊應力與位移影響因素分析

為了研究清管速度、管道內壓、摩擦系數、敷設坡度、清管質量和土壤類型對清管沖擊過程的影響規律，在仿真計算時采取了單因素改變的方法，參數設置情況如表6所示。

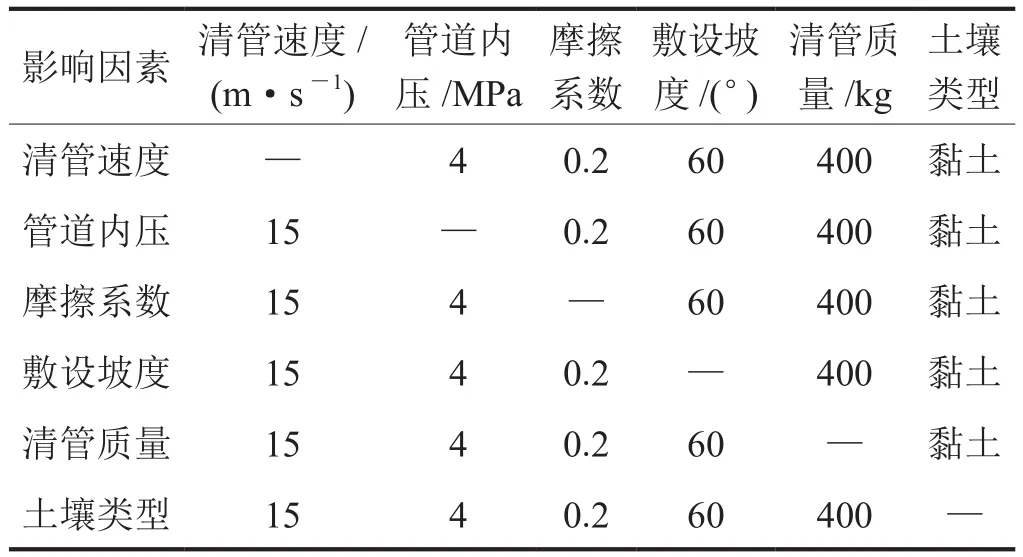
表6 大落差管道清管沖擊應力與位移影響因素參數設置表

2.1 清管速度

為了研究清管速度對大落差管段清管沖擊過程的影響，設置了較寬的速度范圍（3～21 m/s）。不同清管速度條件下，管道所受最大沖擊應力與位移變化曲線如圖3所示。

從圖3可知，隨著清管速度增加，最大沖擊應力增大，并逐漸接近于許用應力值339.5 MPa；最大位移整體上也呈現上升趨勢，尤其是在速度超過12 m/s后，位移值加速上升。其中，應力變化量為88.41 MPa，位移變化量為8.52 mm。這表明清管速度能夠顯著影響清管沖擊過程應力與位移。通過對計算結果進行曲線擬合，得到大落差管道受清管沖擊作用時的最大應力、最大位移與清管速度的關系式。其中，最大應力、最大位移的擬合確定系數（R2）分別為0.989 9、0.968 7。可以看出，最大沖擊應力是隨著清管速度增加而呈現快速上升的趨勢，此時，管道的失效風險也迅速增加，但最大位移在清管速度小于12 m/s時的增加幅度很小。綜上，清管速度會對沖擊過程產生很大影響。

2.2 管道內壓

根據寧納線的實際運行壓力和設計壓力，將壓力研究范圍設置為3.0～6.0 MPa。不同內壓下管道最大沖擊應力與位移變化曲線如圖4所示。

由圖4可知，隨著管道內壓增加，最大沖擊應力快速上升，且最大位移整體上也呈現快速增加的趨勢。其中，當內壓為6.0 MPa時，管道所受最大應力為324.1 MPa，接近管道許用應力339.5 MPa。通過數據擬合可得大落差管道受清管沖擊作用時的最大應力、最大位移與管道內壓的函數關系式。其中，最大應力、最大位移的擬合確定系數（R2）分別為0.995 3、0.986 2。可以看出，擬合曲線呈現平滑上升的趨勢，這表明管道內壓對大落差管段底部彎頭所受的沖擊應力、位移影響顯著。

2.3 摩擦系數

根據《機械清管器技術條件：Q/SY 1262—2010》中關于清管器皮碗材料的規定[19]，將清管器與管壁間摩擦系數研究范圍設置為0.20～0.40。不同摩擦系數下管道最大沖擊應力與最大位移變化曲線如圖5所示。

由圖5可知：①當清管器—管壁摩擦系數由0.20增加至0.30時，最大應力計算值隨著摩擦系數的增加而減小，其變化量為31.48 MPa；最大位移計算值隨著摩擦系數的增加，呈現先增加后減小的趨勢，位移變化范圍為14.8～15.9 mm，但變化量很小，僅為1.1 mm，可以忽略。②當清管器—管壁摩擦系數由0.30增加至0.40時，最大應力、最大位移的計算值均隨著摩擦系數的增加而增加，其中，應力的變化量為31.38 MPa，位移的變化量為2.29 mm。這表明摩擦系數對清管沖擊過程的應力影響較大，而對位移的影響很小。分析最大沖擊應力呈現先減小后增加的趨勢原因為：由摩擦系數變小（或變大）引起的切向沖擊應力減小（或增加）的幅度與由速度增大（或減小）引起的離心力（即施加于管道內表面的正壓力）增加（或減小）的幅度不一致。通過數據擬合可得大落差管道受清管沖擊作用時的最大應力、最大位移與清管器—管壁的函數關系式。其中，最大應力、最大位移的擬合確定系數（R2）均為1.000 0。從擬合曲線可以看出，摩擦系數對清管沖擊過程的應力與位移變化影響存在特殊性。

2.4 敷設坡度

根據天然氣管道敷設時的地形地勢條件，將坡度研究范圍設置為40°～70°。不同坡度下管道最大沖擊應力與位移變化曲線如圖6所示。

由圖6可知，隨著管道敷設坡度增加，即坡度越陡，清管器到達大落差管段底部的速度也會隨之不斷升高，相應的最大沖擊應力、最大位移均快速增大。其中，應力的變化量為91.89 MPa，位移的變化量為4.03 mm。這表明敷設坡度能夠顯著影響清管沖擊過程的應力大小。通過擬合數據可得大落差管道受清管器沖擊作用時，管道最大應力、最大位移與敷設坡度的函數關系式。其中，最大應力、最大位移的擬合確定系數（R2）均為1.000 0，擬合曲線與計算曲線基本重合。從擬合曲線可以看出，管道敷設坡度對清管沖擊應力與最大位移的影響很大。

2.5 清管質量

根據現場清管作業常用清管器類型，包括：直板清管器、測徑清管器、磁力清管器、漏磁檢測清管器的重量變化范圍，將清管質量范圍設置為400～1 600 kg。不同清管質量下管道最大沖擊應力與最大位移變化曲線如圖7所示。

由圖7可知，隨著清管質量的增加，大落差管道受沖擊應力增加或降低幅度并不十分顯著，其中，最大應力的變化范圍為172.43～178.04 MPa，最大位移的變化范圍為15.57～16.80 mm，即應力與位移的改變量均很小。這是因為清管器前后壓差始終設置為0.2 MPa保持不變，隨著清管質量的增加，清管器運行加速度變小，當到達底部彎頭部位時的速度也會減小，從而導致沖擊應力減小，但同時質量的增加會引起沖擊作用力的增加，由此，最終導致管道所受沖擊應力、位移在清管質量改變時未發生較大的且有規律性的變化。為驗證這一結論，通過提取仿真模型中清管器到達底部彎頭時的速度后得出，清管速度確實為隨清管質量的增加而減小。通過擬合數據得出了大落差管道受清管器沖擊作用時，管道最大應力、最大位移與清管質量的函數關系式。其中，最大應力、最大位移的擬合確定系數（R2）分別為0.843 2、0.895 4。從擬合結果可以看出，清管沖擊過程中的應力與位移變化規律不明顯。

2.6 土壤類型

土體性質改變必然導致作用在大落差埋地管道上的載荷發生變化，從而影響清管過程的應力、位移大小。其中，影響土壤彈性模量的黏聚力、內摩擦角是反映土壤性質的重要指標。根據寧納線《線路工程勘察報告》，其土壤主要為粉質黏土和黏土，彈性模量分別為38.54 MPa和28.59 MPa，清管沖擊應力與位移云圖如圖8、9所示。

從圖8、9中可以看出，當管道埋于黏土時，清管過程所受最大沖擊應力與最大位移計算值分別為202.81 MPa、15.24 mm，均大于粉質黏土的應力與位移計算值。這表明粉質黏土嵌固能力強于黏土，管道在受到沖擊載荷作用時，黏土環境下的管道變形更大，因而應力也更大；而粉質黏土環境下的管道被嵌固得更緊，故其位移變化更小。同時，計算結果也表明彈性模量越大的土壤，嵌固能力越強，清管時管道受到的沖擊應力與位移也就越小。

3 大落差天然氣管道清管沖擊過程實例分析

通過綜合考慮不同影響因素，針對寧納線某大落差管段進行清管過程動力學計算。

3.1 清管過程工藝仿真計算

3.1.1 基礎數據輸入

為了建立清管工藝計算仿真模型，獲取清管過程中清管器運行速度隨著位置變化的曲線，需要用到的參數包括：天然氣組分、管道沿線高程、管線長度、管徑、壁厚、粗糙度、輸氣量、首站溫度、末站壓力和環境溫度。以寧納線為例，采用表7中的數據，基于SPT OLGA軟件進行清管工藝計算。

表7 寧納線管道設計及運行參數表

3.1.2 仿真模型建立與校核

選取OLGA Empty File，首末站分別設置為流量節點與壓力節點，并結合管段沿線高程數據，加入FA-models中的清管模塊（Pigging Model），從而起建立管道清管模型。在網格劃分過程中，取每條管段的小節數為4，每節長度取100 m。

通過對寧納線6次清管作業工況進行仿真計算，并將結果與實際清管采集數據進行對比，以驗證所建模型的準確性。首站壓力、末站壓力及平均速度結果對比如圖10所示。

由圖10可以看出，在不同清管工況下，首站壓力、末站壓力及平均速度仿真計算結果與實測之間偏差很小。其中，首站壓力計算結果誤差范圍為0.1%～1.1%；末站壓力計算結果與實測值符合得很好；清管器平均速度計算結果誤差范圍為0.3%～6.4%。因此，采用OLGA軟件所建仿真模型計算準確性高，能夠用于寧納線清管過程的模擬。由此，計算出了輸氣量最大工況（工況3）下清管器通過大落差段的速度為4.3 m/s。

3.2 大落差段清管沖擊過程有限元分析

根據現場某大落差管段的實際路由，針對工況3建立有限元分析模型，參數設置如表8所示。清管沖擊過程仿真計算網格無關性驗證如圖11所示，分別 選 取 了 30×104、35×104、45×104、50×104和55×104共5種不同網格數進行最大應力計算，可以看出當網格數量保持超過45×104個時，應力保持在169 MPa左右，由此確定出模型所用的網格總數為45×104個（實際為451 450）。而清管沖擊過程應力與位移計算結果如圖12、13所示。

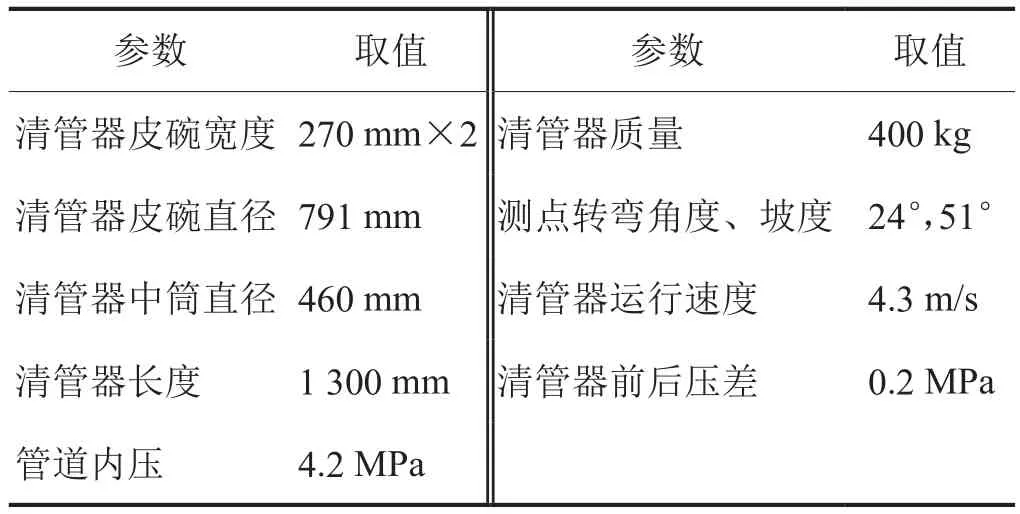
表8 大落差管段清管有限元模型參數設置表

由圖12和圖13可以看出，管道最大應力為168.72 MPa，最大位移為9.29 mm，應力和位移主要集中在彎頭部位。清管過程中清管器的沖擊應力并沒有超過管道的許用應力值349.2 MPa。因此，上述清管作業工況下清管器的沖擊過程是安全的。

3.3 大落差天然氣管道安全清管條件研究

3.3.1 已建大落差天然氣管道

對于已建大落差天然氣管道的某次清管作業而言，可以確定的參數包括：管線敷設路由、管徑、壁厚、大落差段高差與坡度、清管器類型、清管器質量以及清管器—管壁間的摩擦系數。管道輸氣量和運行壓力屬于變量。這兩者均影響清管器運行速度大小，進而影響沖擊過程的應力與位移。

為此，首先通過在仿真模型中逐步增加清管器運行速度，以獲得管道最大應力剛好大于許用應力時對應的清管器速度，即為極限清管速度；然后，通過清管工藝仿真計算得到對應的輸氣量大小，從而獲得以輸量為表征的安全清管工況。以寧納線為例來進行安全清管工況計算：

1）基礎數據輸入。管道內壓取設計壓力6.3 MPa，清管器與管壁摩擦系數取0.2。

2）極限清管速度計算。通過試算不同速度直至管道應力剛好超過管道許用應力349.2 MPa，即為極限清管速度（νmax）。由此可得，當清管器速度為16 m/s時，管道最大應力值為351.1 MPa。

3）最大允許輸量換算。通過改變清管工藝仿真模型起點輸氣量，計算極限清管速度為16 m/s時對應的輸氣量值。由此可以得出，當輸氣量增加至設計輸氣量時，清管器沖擊速度為5.5 m/s，低于極限清管速度，即在清管過程中不會出現管道應力超限的情況。

3.3.2 處于設計階段的大落差天然氣管道

對處于設計階段的起伏地形天然氣管線而言，設計輸氣量和設計壓力均已確定。為此，在管線運行最大輸氣量和壓力條件下，先進行極限清管速度計算，然后基于能量守恒方程式推導出由高程差所表征的安全清管條件計算式。計算公式為：

式中m表示清管器質量，kg；H表示管段的垂直落差，m；F推力表示內壓產生的推力，N；F摩擦表示清管器與管內壁之間的摩擦阻力，N；L表示斜坡內管道長度，m；νmax表示極限清管速度，m/s；ν0表示清管器到達坡頂的速度，m/s；Δp表示清管器前后壓差，MPa；A1表示管道內截面積，m2；f表示摩擦系數；θ表示管道與水平面的夾角，（°）；pr表示清管器與管壁間的接觸應力，MPa；A2表示清管器與管壁的接觸面積，m2。

同樣，以寧納線為例說明如何確定出以高程差為表征的安全清管條件：

1）清管工藝計算。在設計輸量條件下，清管器運行至坡頂時的速度為5.3 m/s。而在計算極限清管速度時，管道內壓取設計壓力6.3 MPa，清管器與管壁摩擦系數（f）取0.2。

2）極限清管速度確定。由3.3.1可知，清管器極限速度為16 m/s。

3）利用式（1）計算得出安全清管高差為852 m。因此，當管道實際敷設的高度小于852 m時，清管過程是安全的；反之，管道則會產生失效的風險。

4 結論

1）隨著清管器運行速度、管道內壓和敷設坡度的增加，清管器對大落差管段底部的沖擊應力值增大趨勢明顯，但位移值漲幅不大。

2）當清管器—管壁的摩擦系數由0.2增加至0.4時，清管沖擊過程的應力與位移變化存在特殊性，且摩擦系數對清管沖擊過程的應力影響較大，而對位移的影響很小。最大沖擊應力呈現先減小后增加的趨勢原因為：由摩擦系數變小（或變大）引起的切向沖擊應力減小（或增加）的幅度與由速度增大（或減小）引起的離心力變化的幅度不一致。

3）對于不同類型的土壤，彈性模量越大，對管道的嵌固能力越強，因而管道所受的沖擊應力與位移也就越小。

4）通過對寧納線某大落差管段進行清管動力學計算，驗證了基于OLGA軟件的清管工藝仿真模型準確性，得出了在目前清管作業工況下，清管器沖擊過程是安全的。

5）通過對已建大落差天然氣管段清管極限速度計算，得到了以輸量為表征的安全清管條件；對于處于設計階段的大落差天然氣管道而言，確定出了以高程差為表征的安全清管條件。