灰狼算法優化分數階模糊控制器參數

范 魯 娜(河南藝術職業學院文化傳播技術學院 河南 鄭州 450002)

0 引 言

分數微積分已經被研究了將近3個世紀，并且已經被科學家廣泛應用到科學與控制工程領域中[1]。分數階PID控制系統是由斯洛伐克學者Podlubny[2]于1994年提出，并應用于分數階模糊系統中。在此項工作之后，其他的工程師應用不同的設計與調整方法設計出分數階PID控制器。分數階微積分為復雜成比例的系統過程和事件提供完善的數學模型，應用于物理、生物與控制理論方面[3-5]。

分數模糊控制器(FFCs)是傳統模糊控制器與分數階算子結合，在多種動力系統中表現出比傳統的模糊控制器更好的性能。分數階模糊控制器中的參數估計問題一般用進化算法去優化求解，提高控制器的精度與穩定性能。例如：用遺傳算法模糊分數階控制器模型問題[6]；用混沌粒子群算法對可再生發電混合動力系統進行分數階模糊控制器[7]；使用微分和聲搜索算法設計分數階[8]；采用改進的重力搜索算法對抽水蓄能水電機組進行快速模糊分數階PID控制[9]；分數階模糊PID控制器在機械手臂中的應用性能分析[10]；社會蜘蛛群算法對分數模糊控制器參數標定[11]。雖然這些算法都獲得比較理想的結果，但是仍然具有一個很重要的局限性，由于其搜索策略中的勘探與開采之間的平衡關系，容易陷入局部最優的解，這種行為會導致整個種群快速集中在最優粒子周圍，容易形成早熟收斂，不利于搜索空間的探索[12-13]。

灰狼優化算法是由Mirjalili等[14]于2014年提出的新型群智能優化算法。灰狼優化算法(GWO)是模擬灰狼的狩獵機制，包括搜索獵物、追蹤獵物、包圍獵物與捕殺獵物等步驟，與其他的元啟發式優化算法不同，該算法考慮領導階層。由于該算法具有較好的平衡勘探與開采能力，所以該算法越來越受到相關領域的人們重視，并成功地應用于一些實際工程問題中。如Gupta等[15]利用GWO對電力系統比例積分控制器的參數進行評估，Chaman-Motlagh[16]利用GWO設計一種具有三到五根橢圓棒的超陷光子晶體濾波器,Sulaiman等[17]利用GWO解決了電力系統中無功優化調度問題。本文用灰狼優化算法優化分數模糊控制器參數，主要是因為灰狼優化算法原理簡單，需要調節的參數少，而且在尋找全局最優解時具有較好的求解效率與較高的求解精度。

1 分數階模糊控制系統數學模型

分數階控制系統的特征是微分方程，在動力系統或控制算法中，分數階通常用微分或積分模型表示[18-19]。

1.1 分數階微積分

(1)

式中：a和t表示操作算子的上下限；α表示分數階階次且α∈R；τ表示切向單位向量。最常用的分數階微積分定義是Riemann-Liouvile(RL)和Grunwald-Letnikou(GL)。分數階微分階α被定義如下：

(2)

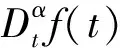
在分數階導數的數值計算中，α階導數在kh(k=1,2,…)點，具體表示如下[11]：

(3)

(4)

然后，分數階差分方程的一般數值解被定義如下：

(5)

1.2 分數階近似值算子

(6)

式中：hα(k)是脈沖序列；Tc表示采樣頻率。在文獻[23]中已經證明了有理式模型比多項式模型具有更快的收斂速度。因此采用Pade近似的方法，利用文中給出的定義，從脈沖響應中得到分數階模型，具體模型表示為：

(7)

式中：m、n與參數ai、bi是通過調節hα(k)的系數m+n+1得到。

2 模糊控制器

模糊控制器是模擬專家的經驗，并用語言形成嚴格的控制規則，然后通過控制規則控制其計算，實現目標任務。模糊控制器的一個重要的特性是將控制方案劃分為多個區域[24]。在每個區域，控制策略都可以通過使用一個規則來簡單地建模，該規則將特定的操作按照所形成的區域關聯起來。在所列出的文獻中，盡管提出了幾種模糊控制器模型配置，但是本文選取模糊分數階PDα+I模型結構，因為此結構具有較好的穩定性與魯棒性[6]。

控制器配置如圖1所示。其中：E、DE和IE分別代表誤差、偏導誤差和積分誤差；e表示偏差值；v表示模糊輸出量；Kp、Kd、Ki、Ku為增益值，前三項表示輸入項，后一項為輸出項。控制函數u是E、DE和IE的非線性映射函數，表示如下：

u(k)=(f(E,CE)+IE)Kuu(k)=[(f(Kpe,KdDαe)+KiIe)]·Ku

(8)

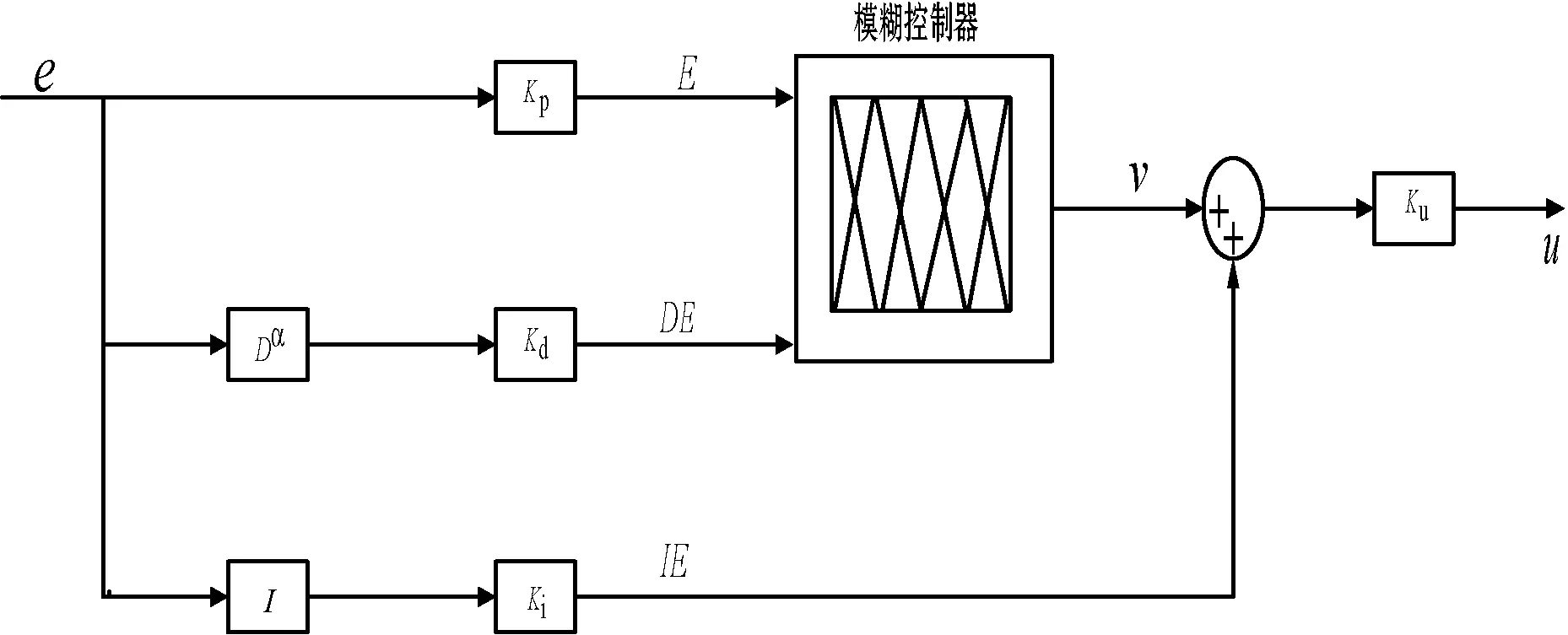
圖1 模糊PDα+I控制器

3 GWO

灰狼優化算法是新型的群智能優化算法[14]，該算法的靈感來源于灰狼群落的領導、指揮與狩獵行為。在該算法中，灰狼群被劃分為四組，分別為α、β、δ、ω，前三種類型是作為領導階層，ω是最底層灰狼種群，追隨前3種種群。α、β、δ灰狼種群的更新公式如下：

D=|C·Xp(t)-X(t)|

(9)

X(t+1)=Xp(t)-A·D

(10)

A=2a·r1-a

(11)

C=2·r2

(12)

式中：D表示灰狼與獵物之間的位置距離向量；t表示當前的迭代時間；A、C是向量系數；Xp是獵物的位置向量；X是灰狼的位置向量；a是步長因子，隨著迭代次數的增加由2降到0；r1、r2取[0,1]間的均勻隨機值。

在GWO中，認定α、β、δ為捕食獵物的最好的值，在優化的過程中，α、β、δ被認為是最好的解，其他灰狼為ω，不斷更新位置朝向α、β、δ種群。根據以下數學模型，調整ω狼群的位置：

Dα=|C1·Xα-X|

(13)

Dβ=|C2·Xβ-X|

(14)

Dδ=|C3·Xδ-X|

(15)

式中：Xα表示α灰狼的位置;Xβ表示β的位置;Xδ表示δ灰狼的位置;C1、C2、C3是隨機值；X表示當前解決方案位置。用式(13)、式(14)和式(15)分別計算當前解位置與α、β、δ灰狼位置之間的距離。定義距離之后，當前解的最終位置計算如下：

X1=Xα-A1·(Dα)

(16)

X2=Xβ-A2·(Dβ)

(17)

X3=Xδ-A3·(Dδ)

(18)

(19)

式(13)-式(15)定義了ω灰狼步長分別朝向α、β、δ灰狼位置。式(16)-式(19)定義了ω灰狼最終的位置。A、C這兩個向量是隨機值，能夠有效平衡GWO勘探與開采能力。

Mirjalili 等[14]提出的GWO相比于其他著名的元啟發式算法具有很高的性能。該算法具有很強的探測能力，而且能夠避免局部最優。此外，較強的平衡勘探與開采能力能夠有效解決一些復雜的工程問題。因此應用GWO優化模糊控制器參數問題。

4 用GWO對分數階模糊控制器參數優化

在分數階模糊控制系統的設計階段，將參數計算過程轉化為一個多維優化問題，將分數階模糊控制器參數作為決策變量。在這種方法中，優化問題的復雜性往往產生多模態誤差曲面，其代價函數往往難以最小化。提出一種分數階模糊控制系統參數優化標定算法，采用GWO確定最優的參數值，如圖2所示。

圖2 基于GWO優化模糊控制器的參數問題

在GWO求解模糊控制器參數問題中，GWO中的最優解表示分數階模糊控制器的一組最優的參數。分數模糊控制器參數(α，Kp,Kd,Ki,Ku)確定GWO候選解的維度。GWO的生物空間對應分數模糊控制器參數整定的解空間。另外，GWO的評價函數是分數模糊控制器的積分時間絕對誤差(ITAE)[25]。ITAE指標J由以下模型定義：

(20)

式中：y(t)表示閉環階躍響應函數;r(t)表示階躍函數。

最小化目標函數為：

J(X)X=(α,Kp,Kd,Ki,Ku)∈R5

(21)

約束函數為:

0≤α≤3

0≤Kp≤5

0≤Kd≤5

0≤Ku≤5

控制器的參數值對控制器的性能具有較高的影響。例如，比例系數Kp值增加時，系統會變得敏感，響應速度更快，系統的穩態誤差得以減小，從而使控制的精度提高。GWO優化的過程是通過連續計算ITAE值來評價該參數的質量，根據GWO的優化規則，通過連續迭代求出ITAE的最小值，從而得到一組分數階模糊控制器的控制參數。

5 實驗仿真

運用灰狼算法優化分數階模糊控制器的參數，主要優化控制器參數α、Kp、Kd、Ki、Ku指標。在比較算法中，將按照各自算法最優的參數值進行設置，表1給出了算法的初始參數設置。

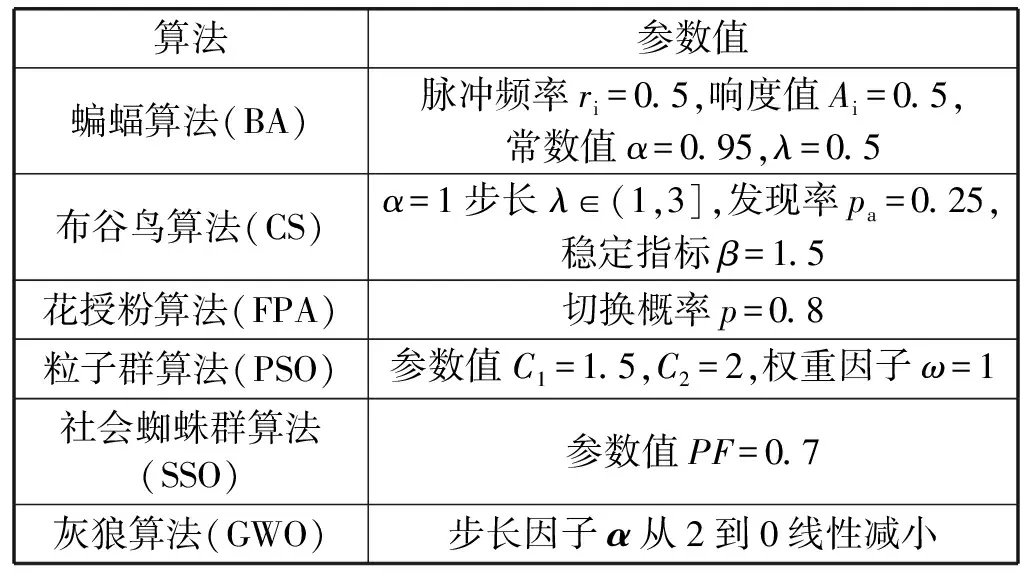
表1 算法的初始參數設置

在MATLAB R2012a上進行實驗，且設置實驗算法中統一種群規模為30，最大迭代次數為30次，獨立運行次數為15次。為了驗證分數階PID模糊控制器的控制性能，采用隸屬函數高階系統對該控制器的性能進行測試，隸屬函數高階系統G(s)表示如下：

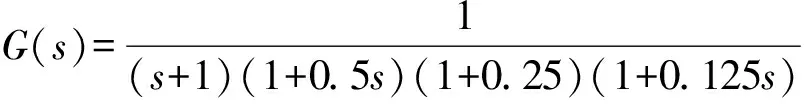
(22)

式中：s表示傳遞函數的復數域。

實驗結果中高階系統G(s)的ITAE表示最優值，表2展示不同算法測試隸屬函數的最好值、最差值、平均值與方差值結果。

可以看出GWO在優化分數模糊控制器參數上獲得較小的適應度值，而且測試隸屬函數高階系統G(s)，取得最小的誤差。這說明GWO比SSO、PSO、FPA、CS和BA優化分數階模糊控制器值獲得較好的結果。

本文實驗考慮到高階動力系統的調節作用，將GWO優化分數階模糊控制器的參數方法與蝙蝠算法、布谷鳥算法、花授粉算法、粒子群算法與社會蜘蛛群算法進行比較。響應時間設置為10 s，設置所有算法的種群數為30個，最大的迭代次數也設置為30次，獨立實驗次數為15次。表3展現了所有算法的優化分數階模糊控制器的最佳參數值以及ITAE的平均值。結果表明，GWO與BA、CS、FPA、PSO和SSO相比具有更好的性能。

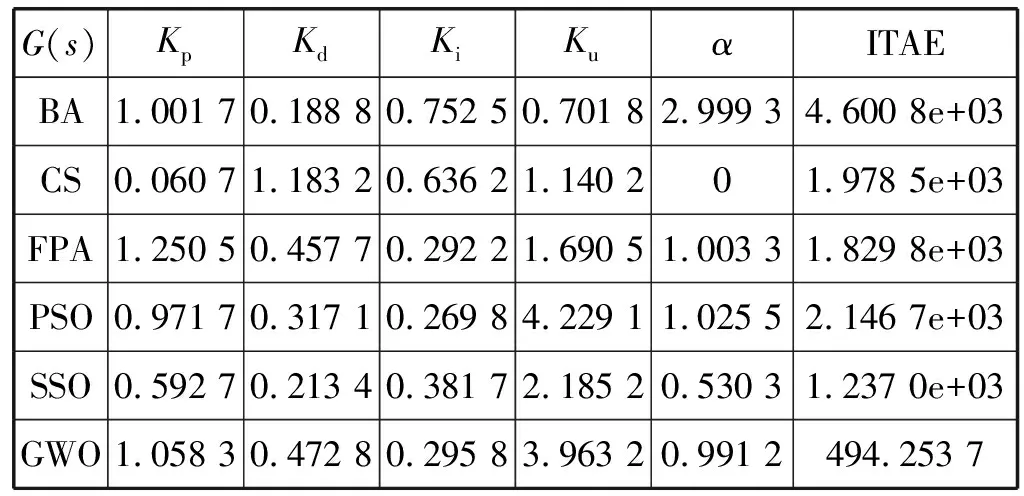
表3 優化算法校準模糊控制器G(s)最佳參數值

圖3顯示不同算法優化分數模糊控制器參數的收斂曲線，可以很明顯看出GWO在優化分數階問題獲得較快的收斂速度，而且穩態誤差也是最小的。圖4展現高階系統G(s)在不同算法所優化最佳參數值下的階躍響應曲線，很明顯在GWO優化分數模糊控制器參數下的隸屬函數G(s)階躍曲線有著更加平穩、超調量小、調節時間短、響應時間快等較好的動態性能。

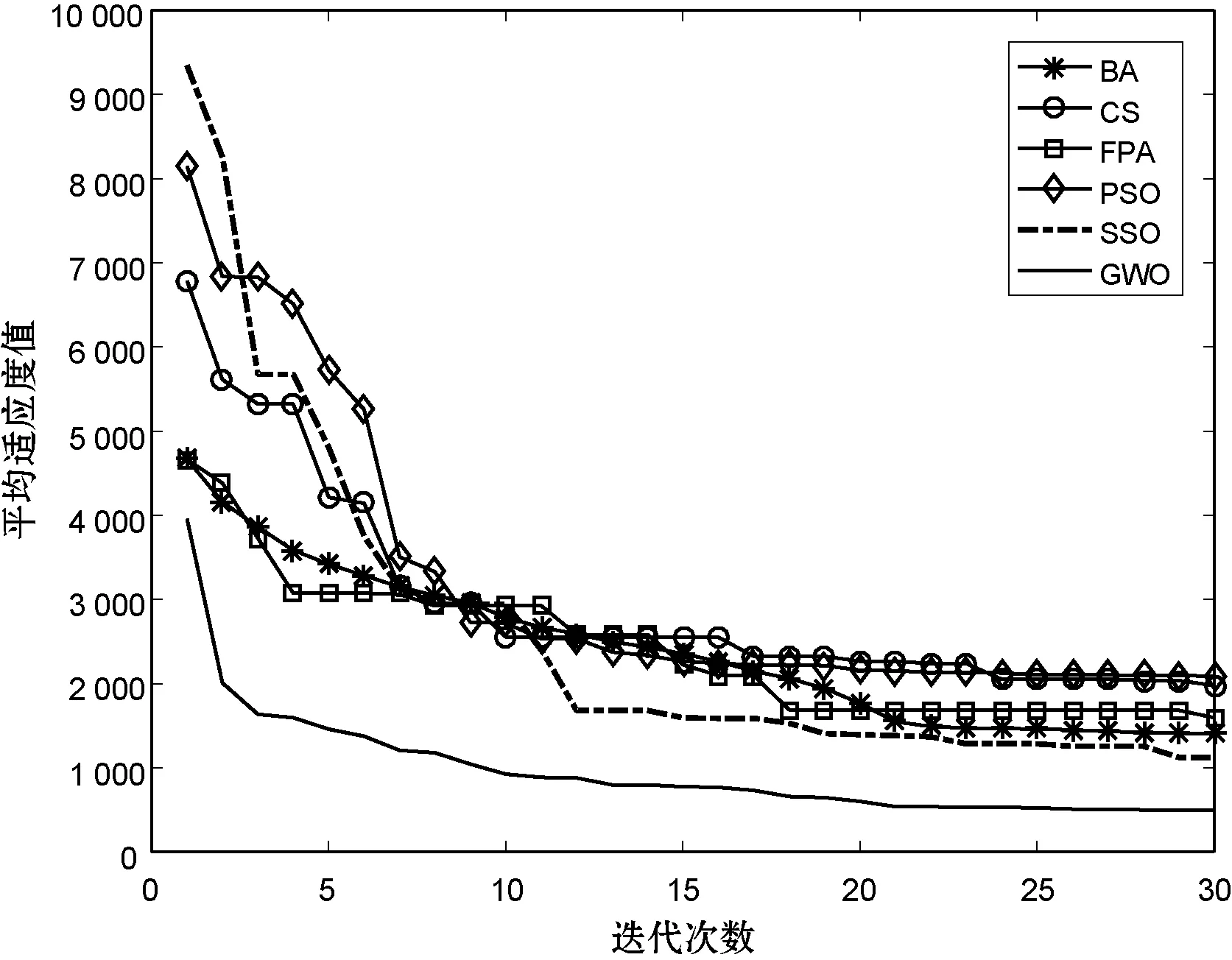
圖3 G(s)不同算法的收斂比較

6 結 語

本文提出一種基于灰狼算法的優化方法優化分數模糊控制器參數問題。GWO是一種新型的元啟發式群智能算法，靈感來源于灰狼的捕食與社會等級等習性。該算法明確個體集中最優位置，避免因次優解的過早收斂、勘探與開采之間的不平衡關鍵缺陷。為了說明該算法優化參數問題的有效性與魯棒性，針對高階系統G(s)，通過GWO進行實驗評價。為了評估GWO優化參數問題的性能，將該算法與蝙蝠算法、布谷鳥算法、花授粉算法、粒子群算法和社會蜘蛛群算法比較，實驗結果表明，該方法在求解質量和收斂性方面優于其他方法。