加勁鋼桁連續剛構橋地震易損性分析

李 龐

（中鐵六局呼和浩特鐵路建設有限公司，內蒙古 呼和浩特 010050）

0 引言

橋梁作為交通路網中的連接構件，是保證交通順暢和經濟發展的關鍵組成部分，橋梁結構在地震作用下發生損傷，會嚴重影響社會和經濟發展，所以橋梁的地震損傷分析具有舉足輕重的意義。大跨度連續剛構橋由于其外觀優美、克服復雜地形能力強等優點，在交通路網建設中被廣泛應用，同時，由于其后期保養難度高，對其抗震性能的研究也一直是熱點話題。因此，對高墩大跨度加勁鋼桁架連續剛構橋在地震作用下的抗震性能研究是有必要的。

目前，國內外學者對橋梁抗震性能研究頗多。在基于 IDA 的倒塌易損性分析方法，國內代表學者有黃盛楠［1］、谷音［2］、吳文朋［3］、陳志偉［4］、周長東［5］等，上述學者分別以不同類型的橋梁為算例進行橋梁抗震性能研究。國外學者 Hwang［6］針對缺乏地震破壞數據地區的橋梁，基于場地特征構造了人工地震動，對該區域典型橋梁進行了地震易損性分析。對現場試驗和理論分析之間的差異比較，國外學者 Tavares［7］以加拿大魁北克省三河市的橋梁為例進行了相關研究。

在各損傷狀態下，系統的損傷概率均大于構件的損傷概率［8］，因此需要探究橋梁構件之間的相關性，對橋梁系統進行易損性計算。本文首先介紹了地震易損性分析流程，然后以某座加勁鋼桁架連續剛構橋為例，基于增量動力分析方法，選取了 10 條地震波，對結構進行了非線性時程分析，比較了構件與系統兩個層面的橫向地震易損性。

1 易損性分析流程

本文以一座加勁鋼桁架連續剛構橋為工程背景，借助有限元軟件 MIDAS Civil，通過纖維截面劃分實現非線性，建立全橋有限元模型。將橋墩作為易損構件，在橋墩墩頂、墩底添加纖維鉸，計算在地震荷載的作用下橋墩在該位置的響應，繼而得到構件地震易損性曲線，基于一階界限估計法，計算該橋的系統易損性。

結構發生某種程度破壞的概率，如式（1）所示。

式中：IM為地震動參數；DI為地震需求；C為抗震能力。

本文基于理論易損性分析方法計算結構系統的易損性曲線，其分析流程如圖 1 所示。

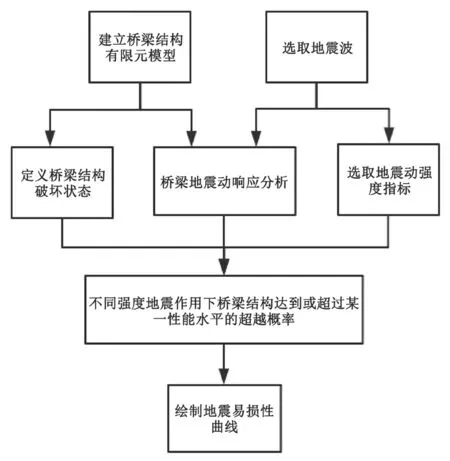
圖1 地震易損性分析流程

2 工程概況與有限元建模

2.1 工程概況

算例橋梁為一座四跨（97+2×180+97）m 加勁鋼桁架連續剛構橋，主梁頂板寬 15.0 m，底板寬 11.5 m，頂板、底板和腹板厚度分別為 0.5～1.7 m、0.45～2.5 m 和 0.45～1.5 m。箱內頂、底板處分別設150 cm×50 cm、45 cm×45 cm 梗脅。中支點處橫隔墻厚 150 cm，并設有 170 cm×200 cm 進人孔，端支點處橫隔墻厚 150 cm，并設有 160 cm×160 cm 進人孔。橋墩編號從左到右依次為 1 #～5 #，其中最高墩為 4 # 墩，墩高 105 m，設置豎桿三角形加勁鋼桁，整體式節點，中跨 158 m 范圍內設置加勁鋼桁，節間長度 12.5 m，主桁中心距 11.5 m，桁高 12.5 m。

2.2 有限元建模

根據橋梁所處場地條件，運用 MIDAS CIVIL 建立全橋非線性有限元模型，如圖 2 所示。

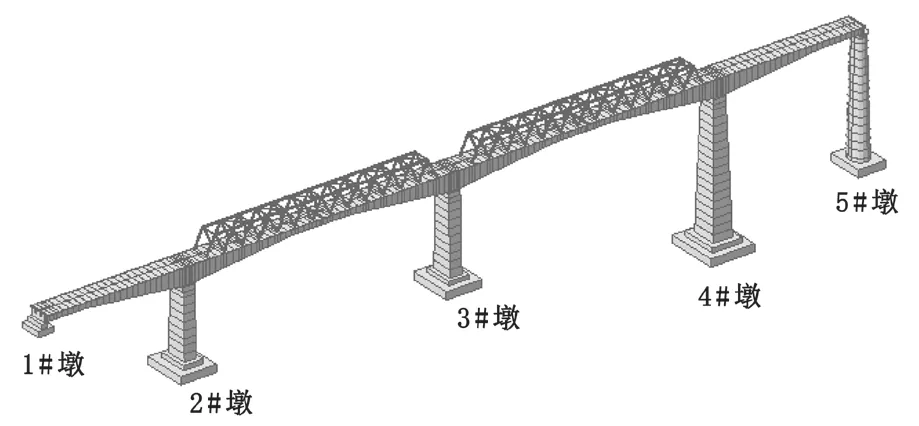
圖2 算例橋梁有限元模型

2.3 自振特性

自振特性分析是抗震計算的基礎，表 1 為該橋前五階自振特性。

表1 自振特性

該加勁鋼桁架連續剛構橋的第一階振型為 3#、4# 橋墩以及主梁橫橋向振動，2# 橋墩沒有明顯橫橋向振動，橋梁與橋墩在豎向以及順橋向沒有明顯振動；第二階振型為 2#、3# 橋墩以及主梁橫橋向振動，4# 墩沒有明顯橫橋向振動，橋梁與橋墩在豎向以及順橋向沒有明顯振動。其自振特性分析表明，相比于豎橋向和縱橋向，該橋在橫橋向的抗震性能較差。因此本文主要分析背景橋梁在橫向地震作用下的易損性。

3 損傷指標

在地震易損性分析中，一般將結構損傷狀態劃分為如表 2 所列的 5 個損傷等級［9］。根據既往研究表明，高墩橋梁由于高階振型影響，導致墩頂位移與墩底彎矩出現不一致的現象，因此選用曲率延性比作為橋墩的損傷指標。

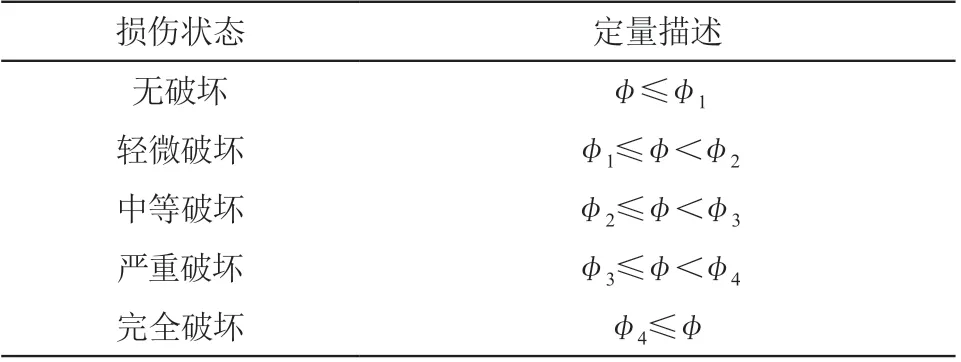
表2 橋墩曲率延性比定義的破壞狀態

借助 X-TRACT 軟件，對背景橋梁易損構件進行彎矩-曲率分析，其中φ1為首次屈服曲率；φ2為等效屈服曲率；φ3為混凝土壓應變達到 0.004 時對應的曲率；φ4為截面極限曲率。

4 地震易損性分析

對選用的 10 條天然地震波進行步長 0.1g的等步長為調幅，調幅區間為 0～1.0g。輸入有限元模型并進行非線性分析。

4.1 構件地震易損性

構件易損性分析中，用目標構件需求Sd和其承載能力Sc來計算超越概率，如式（2）所示。

由于Sd和Sc都服從對數正態分布，式（2）可轉化為如下所示形式，如式（3）所示。

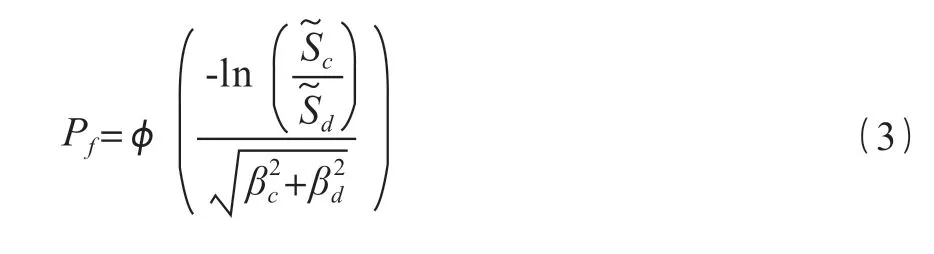
橋墩需求響應的對數值 ln（μ1）與地震峰值加速度對數值 ln（PGA）的線性回歸分析結果如圖 3 所示。

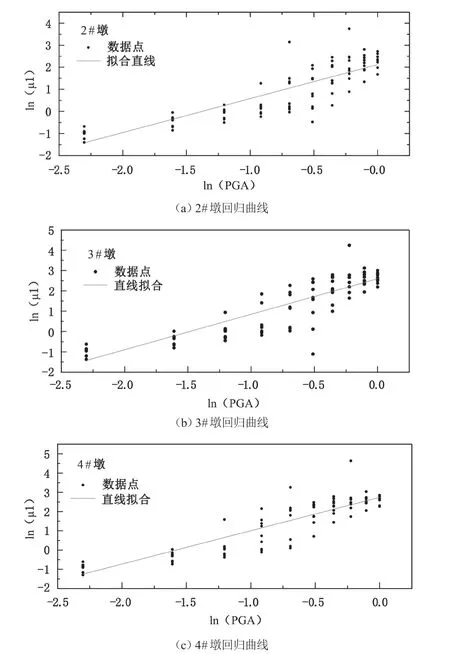
圖3 不同構件地震需求響應的回歸分析

本文中結構反應需求服從對數正態分布，如式（4）所示。

式中：為結構需求平均值；βd為結構需求對數標準差。

依據圖 3 所示的線性回歸分析結果，得出了如表 3 所列的回歸曲線的擬合函數。

表3 不同構件地震響應的概率需求模型

表 3 結果帶入公式（3），并進行計算可以得到各橋墩在不同損傷狀態下的超越概率。最后以地震動峰值加速度為x軸，構件的損傷超越概率為y軸，繪制如圖 4 所示的加勁鋼桁架連續剛構橋各橋墩地震易損性曲線。

由圖 4 可知，隨著 PGA 的的增大，各構件在地震荷載作用下對應各級損傷狀態的概率呈增大趨勢。在E1（PGA=0.15g）地震作用下 2 # 橋墩、3# 橋墩、4# 橋墩的輕微損傷概率分別是 5.47 %、9.68 %、13.15 %。在E2（PGA=0.32g）地震作用下 3# 橋墩、4# 橋墩發生中等損傷的概率為 65.15 %、67.18 %，均超過 50 %，且其發嚴重損傷的概率分別為 3.64 %、4.91 %。對于同一構件而言，隨著地震動強度的增大，其破壞概率也呈增大趨勢，各級易損性曲線呈現先快速增加后逐漸變緩，表明構件進入延性耗能階段。

圖4 4 種損傷狀態構件地震易損性曲線

4.2 系統地震易損性

計算橋梁系統易損性時，需從構件易損性出發，用若干構件的易損性去表征系統易損性。本文采用一階界限法［10］計算橋梁系統失效概率：

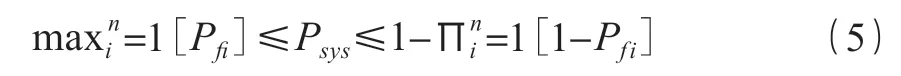
式中：Psys為系統是失效概率；Pfi為第i種構件失效的概率。

采用一階界限法時，其構件破壞概率的最大值是系統失效概率的下限值，其上限則是則所有構件全部失效的概率。由于未考慮構件之間的相關性，因此給出的上下限區間較寬。繪制得系統易損性曲線，如圖 5 所示。

在E1（PGA=0.15g）地震作用下系統的輕微損傷概率的上限為 28.94 %，相較于 2# 橋墩、3# 橋墩、4# 橋墩的 5.47 %、9.68 %、13.15 %，增大幅度為 99.82 %。在E2（PGA=0.32g）地震作用下系統發生嚴重損傷的概率幾乎達到了 30 %，遠大于同等條件下 2# 橋墩、3# 橋墩、4# 橋墩的嚴重損傷概率。其系統易損性同構件易損性變化趨勢相同，隨著地震動強度的增大，其破壞概率呈增大趨勢，易損性曲線也呈現先快速增加后逐漸變緩。通過將圖 5 與圖 4 進行對比發現，在各損傷狀態下，系統的損傷概率相較于構件均會有不同程度的增長，僅從單個構件角度評價橋梁抗震性能是偏安全的。

圖5 4 種損傷狀態系統地震易損性曲線

5 結論

1）該算例橋梁前四階振型均為橫橋向振動，第一階振型與第二階振型有接續跡象，且第三階、四階振動振型與第一階、二階振型相似。表明振動情況延橋向傳播，且在振型疊加下振動幅值有所增加。

2）該算例橋梁在E1（PGA=0.15g）、E2（PGA=0.32g）地震作用下 2# 橋墩、3# 橋墩的輕微損傷概率和中等損傷概率均小于 4# 橋墩，表明在同一地震強度的作用下，構件損傷超越概率與橋墩高度有一定關聯。對于該橋各級損傷狀態，構件損傷概率與墩高呈正相關，即 4# 墩＞3# 墩＞2# 墩；各個損傷狀態下，地震動峰值加速度與構件的損傷超越概率成正相關。

3）在各損傷狀態下，系統的損傷概率相較于構件均會有不同程度的增長；在進行結構的抗震性能評估時，僅從單個構件角度進行分析是偏安全的，還需考慮系統內各構件之間的相關性。Q