矮塔斜拉橋設計參數對主梁受力及變形的影響

王汪陽

（新疆兵團勘測設計院（集團）有限責任公司，新疆 烏魯木齊 830002）

引言

近年來，矮塔斜拉橋因具有外型美觀、經濟合理、施工簡便及跨徑布置靈活等特點，逐漸在我國橋梁事業中得到廣泛應用［1］。但在早期完工的矮塔斜拉橋工程中，由于設計者對橋梁部分參數的分析不足，導致橋梁出現主梁大幅度變形、受力不均等嚴重病害［2-3］。因此，為保障矮塔斜拉橋運營的安全性，深入研究其參數設計具有重要意義［4］。

目前，國內外學者關于斜拉橋的參數設計問題展開了大量研究，張欣欣［5］針對矮塔斜拉橋結構體系、合理結構參數、斜拉索張拉方案等關鍵技術進行分析研究，發現采用剛構連續梁體系，輔以外伸跨，可以有效地減小下部結構受力，同時滿足剛度要求，結構經濟合理。鮑英基等［6］對PC 矮塔斜拉橋運營階段主梁的應力和位移進行敏感性分析，得出主梁應力和位移隨各參數的變化規律。上述學者主要是針對傳統斜拉橋進行的參數設計研究，而關于矮塔斜拉橋的參數設計研究還有待進一步完善。

1 工程概況

某大跨度雙塔混凝土矮塔斜拉橋+先簡支后連續預應力T 梁組合體系橋梁全長475 m，主橋跨徑布置為80 m+145 m+80 m，引橋跨徑布置分別為2×40 m和3×30 m，橋面總寬25 m，包含2×0.5 m 防撞護欄+2×11 m 行車道+2 m 中央隔離帶。道路設計為雙向四車道，設計速度為80 km/h，設計荷載為公路-Ⅰ級，地震動峰值加速度為0.2 g。矮塔斜拉橋主梁采用單箱三室斜腹板變截面箱梁，頂板寬12 m，底板寬6.8 m，支點處梁高5.8 m，跨中梁高2.8 m，呈二次拋物線形式變化，斜拉索張拉位置的箱梁內每隔6 m 設置一橫隔板，厚度為40 cm。主梁與主塔采用塔梁固結體系，主塔采用矩形斷面，截面尺寸為5 m×2.4 m，橋面以上塔高為24 m，主塔對稱設置斜拉索17 對，呈單索面扇形布置。梁上間距為7 m，塔上間距為1 m，邊跨無索區長度為18 m，中跨無索區長度為21 m，斜拉索通過塔身分絲管鞍座，對稱錨固于梁體上，間隔1 m。矮塔斜拉橋總體布置見圖1。

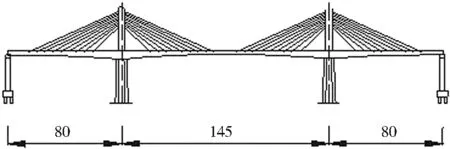
圖1 矮塔斜拉橋總體布置/m

2 建立模型

運用軟件Midas/Civil 建立矮塔斜拉橋有限元模型，其中主梁、主塔及橋墩均采用梁單元模擬，采用桁架單元模擬斜拉索，全橋共包含58 個桁架單元、182 個梁單元和276 個節點，有限元模型見圖2。

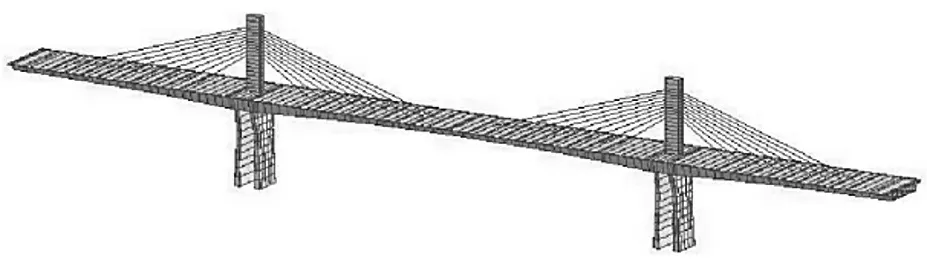
圖2 矮塔斜拉橋有限元模型

計算過程中考慮初始張拉力的影響，斜拉索的初始張拉力均為5 600 kN，斜拉索的彈性模量取值按鋼絞線實際彈性模量，但考慮到防腐材料的重量，斜拉索的容重增加10%。主梁與主塔節點之間采用固結連接形式，主梁與橋墩節點采用剛接連接形式，不考慮主梁、主塔及橋墩的幾何非線性變形對結構的影響，模型基礎邊界條件采用相應剛度矩陣方法模擬。計算荷載主要考慮恒載、活載、掛籃與濕重荷載，混凝土的收縮徐變作用及溫度荷載的影響。鋼絞線及預應力鋼筋計算參數見表1。

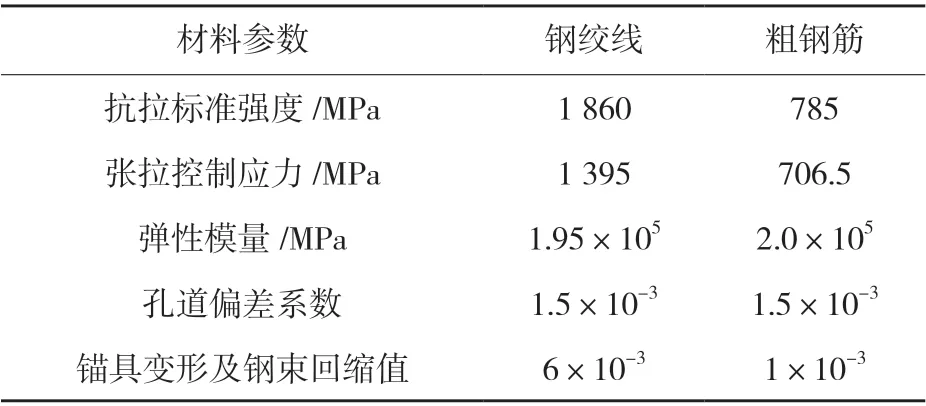
表1 鋼絞線及預應力鋼筋計算參數

3 結果分析

在矮塔斜拉橋的設計中，邊中跨比與主塔高度的參數選取是一個非常重要的結構參數設計步驟，合理的參數選取可有效提升矮塔斜拉橋的經濟性和力學性能。為了研究參數對矮塔斜拉橋的影響，通過建立模型對橋梁受力及變形情況展開對比分析。

3.1 邊中跨比

建立邊中跨比分別為0.52、0.54、0.56、0.58 及0.6 的矮塔斜拉橋模型。針對不同邊中跨比的主梁邊、中跨撓度及彎矩進行計算，得到最大撓度及彎矩變化曲線見圖3。

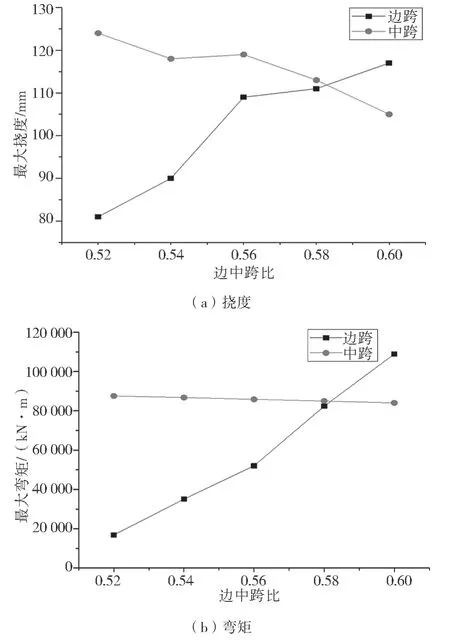
圖3 最大撓度及彎矩變化曲線

根據圖3 可知：（1）隨著矮塔斜拉橋邊中跨比不斷增大，主梁邊跨的最大撓度呈增大的趨勢，而中跨最大撓度呈減小的趨勢變化，說明邊中跨比對矮塔斜拉橋變形的影響較大。當邊中跨比由0.52 增至0.6 時，主梁邊跨最大撓度由81 mm 增至117 mm，增幅為41.3%，而中跨最大撓度由124 mm 減小至105 mm，減幅為15.3%，說明增大邊中跨比雖然可以一定程度降低主梁中跨變形量，但會大幅度增大邊跨變形量。（2）隨著矮塔斜拉橋邊中跨比的增大，主梁邊跨最大彎矩均呈不斷增大的趨勢，中跨的最大彎矩呈緩慢減小的趨勢，說明邊中跨比對矮塔斜拉橋受力存在影響。當邊中跨比由0.52 增至0.6時，主梁邊跨最大彎矩由16 846 kN·m 增至108 886 kN·m，增幅為546%。而主梁中跨最大彎矩由87 525 kN·m 減至84 002 kN·m，減幅為4%，說明增大邊中跨比會大幅度增加矮塔斜拉橋主梁邊跨受力，不利于結構的安全性。

3.2 主塔高度

建立塔高分別為18 m、22 m、26 m、30 m 及34 m的矮塔斜拉橋模型，針對不同塔高的橋梁邊、中跨撓度及彎矩進行計算，得到最大撓度及彎矩變化曲線見圖4。

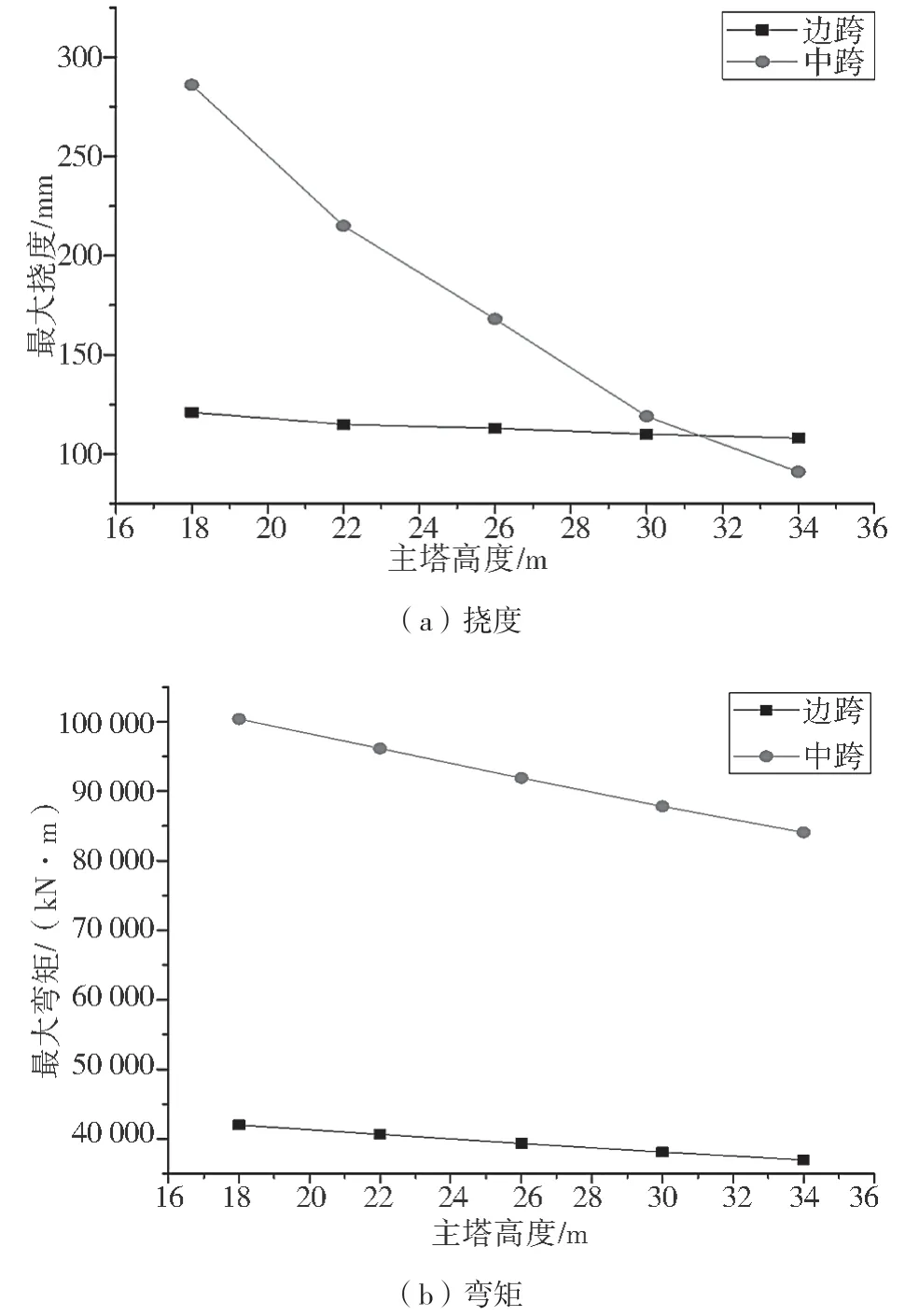
圖4 最大撓度及彎矩變化曲線

根據圖4 可知：（1）矮塔斜拉橋邊、中跨最大撓度均隨著主塔高度的增大而不斷減小，說明邊中跨比對矮塔斜拉橋變形的影響較大。當主塔高度由18 m 增至34 m 時，主梁邊跨最大撓度由121 mm減至108 mm，減幅為10.7%，而中跨最大撓度由286 mm 減小至91 mm，減幅為68.1%，說明增大主塔高度可以大幅度降低主梁中跨的變形量。（2）隨著矮塔斜拉橋主塔高度的增大，主梁邊、中跨最大彎矩均呈不斷減小趨勢，說明邊中跨比對矮塔斜拉橋受力存在影響。當主塔高度由18 m 增至34 m 時，主梁邊跨最大彎矩由42 003 kN·m 減至36 984 kN·m，減幅為11.9%，而主梁中跨最大彎矩由100 386 kN·m 減至84 071 kN·m，減幅為16.3%，說明增大主塔高度可以有效降低矮塔斜拉橋整體結構受力。

4 結語

（1）斜拉橋主梁中跨最大撓度隨著邊中跨比的增大逐漸減小，而主梁邊跨的最大撓度隨之逐漸增大；主梁中跨的最大彎矩隨著邊中跨比的增大呈略微減小，主梁邊跨最大彎矩則隨之逐漸增大；邊中跨比過大對主梁邊跨的撓度、彎矩影響明顯。（2）隨著主塔高度的增大，主梁邊、中跨的最大撓度均逐漸減小，且邊跨減幅更明顯；主梁邊、中跨的最大彎矩均隨主塔高度的增大逐漸減小。