基于GNSS-IR技術高精度水庫水位監測研究
宋敏峰,何秀鳳
(河海大學 地球科學與工程學院,江蘇 南京 211100)
0 引言
近年來,基于全球導航衛星系統(Global Navigation Satellite System,GNSS)反射信號的遙感技術持續受到關注,由于GNSS信號具有免費和信號源豐富等特點,促使該技術在天、空、地3個維度全面發展[1-2]。基于地面GNSS觀測站的干涉測量(GNSS Interferometry Reflectometry,GNSS-IR)技術為近地表環境(土壤濕度、雪深、雪水當量、植被、潮汐等)的監測提供了更多可能[3-4],其中基于該技術利用沿海GNSS測站為海平面長期監測提供了一種新的低成本手段。已有多位研究學者基于傳統的監測站驗證了GNSS-IR潮位監測的可行性和有效性[5-7],且監測精度均可達到10 cm,相關系數均可達到0.97[5],但該技術應用于內陸水域的水位變化監測較少。許多大型調蓄水庫等儲水基礎工程為保障水庫大壩安全均安裝了GNSS大壩形變監測系統,同時也設立了專門的水位監測以確保水資源的優化調度。而GNSS-IR技術可以充分利用該測站進行水位的監測以節省大量的人力物力,但目前該方法還未有效推廣。針對于此,本文在經典潮位反演方法的基礎上,給出了基于GNSS-IR技術的內陸水庫低成本、高精度的水位監測方法。
1 方法與原理
多路徑的產生非常復雜,GNSS-IR技術可以充分利用被擯棄的低仰角數據實現高度變化反演,如水位的變化、雪深的監測[8]等。GNSS-IR水位監測如圖1所示,沿海測站天線接收到的是由直射信號和經由水面反射的信號干涉合成的GNSS多路徑信號。

圖1 GNSS-IR水位監測Fig.1 GNSS-IR water level monitroing
圖1中,h為天線相位中心距離水面的距離,由于地基的監測范圍小,且反射點與測站的距離相對于衛星至接收機的距離很小,可認為水面反射點處至衛星的高度角與接收機處相等,因此基于圖1所示的幾何條件,可得到直射信號與反射信號之間的傳播路徑差 ?為:
?=2hsinθ,
(1)
式中,θ為天線相位中心處的衛星高度角;h為天線相位中心距離水面的距離。由式(1)可知,天線距離水面的高度以及高度角的變化會影響反射信號與直射信號傳播的路徑差,且直射信號與反射信號同時到達接收機處時會產生干涉效應,該干涉效應并不需要直接測量,而GNSS 觀測文件中的信噪比(SNR)可以體現。基于多路徑干涉信號仿真軟件MPSIM可以仿真不同地表環境和不同天線高度等多參數控制的SNR[9],如圖2 所示。
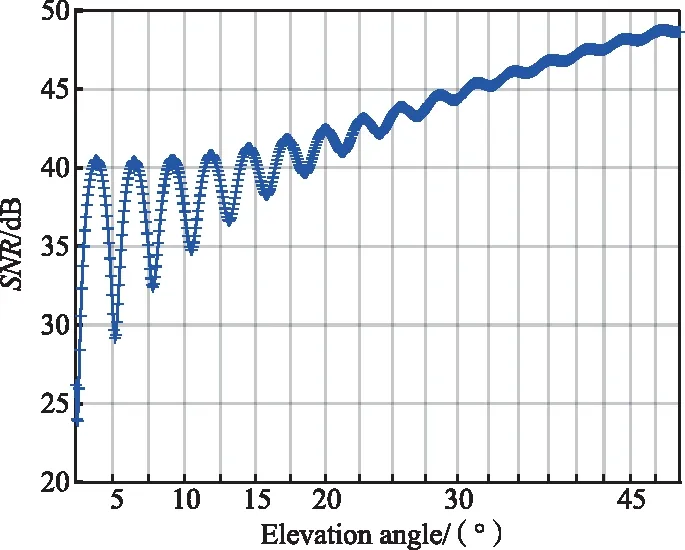
圖2 天線距離反射面高度為2 m的SNR仿真示意Fig.2 Simulations of the SNR of the antenna at a height of 2 m from the reflector
由圖2可以看出,在低高度角條件下,信噪比數據呈現周期振蕩趨勢,周期振蕩隨著高度角的增大,振蕩振幅趨勢逐漸減小。而造成該振幅減小的原因是多方面的,主要與3個因素有關:第一是天線的增益模式。由于GNSS為右旋圓極化信號,且GNSS天線也為右旋圓極化,從而避免左旋圓極化方式的信號。右旋圓極化GNSS信號經過地物反射會隨著高度角的變化呈現不同的左右旋圓極化比,在低高度角單次反射時,反射信號以右旋圓極化占主導,高度角越高,天線能接收到的反射信號中右旋圓極化成分越少,從而信噪比不再具有振蕩效應。第二,天線增益隨著入射信號從俯視入射到仰視入射逐漸減小,在低高度角時,為反射信號相對于直射信號強度最大的時刻,這也是大地測量型應用中需要設置截止高度角的原因。第三,受到反射面的影響,根據瑞利準則,高度角越低,反射面相對于入射電磁波越光滑,此時反射的信號強度也越大[10]。除了振蕩趨勢的衰減,該振蕩的周期性與天線相位中心距離反射點的垂直高度相關[11],由圖1和式(1)可知,高度越高,直射信號與反射信號之間的傳播延遲差越大,在相同的時間內,延遲相位變化越快。因此,可以通過提取該振蕩頻率求解該距離差。對圖2中SNR可認為主要由2部分組成[12]:
SNR=SNRd+dSNR,
(2)
式中,SNR為觀測文件信噪比序列;SNRd為直射信號主導的信噪比主趨勢;dSNR為有反射信號與直射信號干涉導致的殘余SNR。一般可用對低高度角區間段SNR進行低階多項式擬合的方式去除主趨勢而得到殘余信噪,對殘余SNR進行頻譜分析可得到其振蕩頻率f。dSNR可建模如下[13]:
(3)
式中,Pref為反射信號強度,該參數主要影響SNR周期振蕩的振幅大小;h為天線距離反射面的垂直距離;ξ為殘余SNR振幅衰減因子,其大小主要影響SNR振蕩衰減快慢,與反射面的粗糙度、反射面介質和天線增益等相關;κ為載波波速;φ為隨機誤差相位值。由于SNR隨高度角的變化為非均勻的,本文采用Lomb-Scagle 譜分析方法[14],另外也可使用其他分析方法[10]。得到頻率f后,進一步可以得到天線相位中心至反射面的高度:
(4)
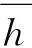

(a) 1.5 m

(b) 4 m圖3 天線高度為1.5,4 m時SNR仿真及其頻譜分析結果Fig.3 SNR simulation and spectrum analysis results for antenna heights of 1.5 m and 4 m

另外,由于該方法是基于反射面的高度在殘余SNR時間段內不變的假設,因此需要進一步添加潮位動態改正,可以得到反射面的高度Href[15]:
(5)
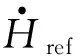
2 數據集
為驗證GNSS-IR方法在水庫測站上的應用效果,選擇雙王城水庫大壩穩定性監測系統的GNSS測站進行分析,測站分布如圖4所示。

圖4 雙王城水庫大壩GNSS形變監測系統測站Fig.4 GNSS deformation monitoring system stations at Shuangwangcheng reservoir dam
雙王城水庫位于山東濰坊壽光市,水庫大壩軸線總長達到9.636 km,壩高12.5 m,最大庫容量達到6 150萬立方米,是南水北調東線膠東干線工程的重要調蓄水庫。為了監測水庫大壩的穩定性,在大壩周圍建立了3個監測站和1個基準站,其中SW43點為基準站,距離大壩約300 m,SW50,SW51,SW52均為監測站,通過觀測墩方式安裝于大壩壩頂水庫內側。位于SW50監測點附近有1個人工讀尺方式的水位監測站,記錄每日的水位,可作為交叉驗證數據進行精度評定。實驗收集了2017年7月1日—12月31日SW51監測站的觀測數據以及對應時期水位監測站的水庫日實測水位數據。GNSS接收機的觀測數據采樣間隔為15 s,且可以觀測到GPS和BDS衛星多頻觀測數據。測站位置的水域方位角為130°~225°,高度角截取范圍為5°~15°。
3 驗證
如前所述,GNSS-IR技術監測水位的主要方式是通過獲取天線至水面的垂直距離間接得到反射面的高度,而此時水位站的實測水位基準為該水庫獨立水位基準,且該基準與大地測量坐標不統一,未知天線相位中心在該水位高程基準的高度,所以此處通過最小二乘方式基于GPS SIC SNR的水位結果得到SW51測站天線相位中心在水位高程基準中的高度。
3.1 水位監測結果
對2個測站收集的GPS和BDS雙系統的數據進行分析,并采用LSP譜分析方法提取主頻率,2種系統的多個頻率的結果如圖5所示。

(a) SW51測站,基于GPS系統 S1C,S2L和S5Q信噪比數據得到的水位結果

(b) SW51測站,基于GPS系統 BDS系統S1I ,S7I和S6I圖5 基于GPS和BDS系統6個頻段數據的水位監測結果Fig.5 Water level monitoring results based on six frequency bands of GPS and BDS systems
為了便于評估精度,對GNSS-IR方法反演的水位進行平均濾波處理得到日平均水位結果。由圖5可以看出,基于GPS和BDS系統的不同類型SNR數據均可以通過GNSS-IR方法有效且準確地監測水位變化。與實測水位相比,總體趨勢幾乎一致,經過統計分析,不同頻段的SNR數據得到的日平均水位精度約為3~4 cm,且相關系數均達到0.99以上,但同時也可以發現,不同頻段數據之間存在較小的系統偏差,使得在同一水位基準下不同頻段數據的結果出現整體偏移現象,需要進一步分析和改正。
3.2 多頻間偏差分析及改正
基于同一測站的天線和接收機之間存在不同大小的系統性偏差,該偏差包含了天線接收不同頻率的相位中心間距以及其他未知誤差。經過進一步分析,除了系統偏差外還存在隨高度變化的線性誤差,如圖6所示。
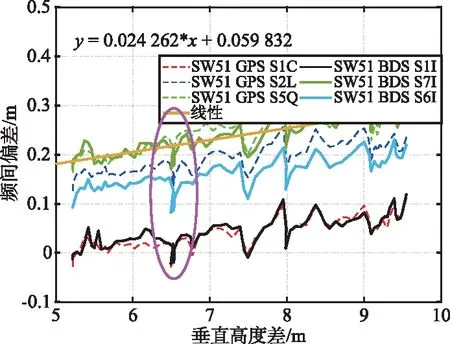
圖6 多頻段數據水位反演結果的系統偏差及線性誤差Fig.6 System deviationand linear error of water level inversion results of multi-band data
由圖6可以看出,在不同高度差的條件下,GNSS-IR方法存在一個隨高度差變化的系統誤差,可根據圖中橢圓區域的水位變化分析確定。在該區間內,不同頻段的結果均存在聚集現象,該結果與圖5中年積日為330~340之間的水位對應。由于此時的水位幾乎未發生改變,因此表明在不同的高度差情況中,該偏差與高度差有關,與文獻[15]得到的結論相一致。通過擬合的方式進行系統偏差和線性偏差改正可以進一步提高水位監測結果的精度:
(6)


表1 SW51 測站基于GNSS-IR方法的水位監測結果統計Tab.1 Statistics of water level monitoring results based on GNSS-IR method at SW51 station
表1中,σpre為線性誤差改正前的精度,σpost為線性誤差改正后的水位反演精度,不同系統的不同頻段誤差系數較小,基本在0.017~0.024,這表明1 m的高差可能會導致1.7~2.4 cm的線性誤差,如果在基于該方法監測水位變化范圍較大且要求精度較高的情況下,需要考慮此誤差。經過多項誤差改正后,多個頻段的水位反演結果精度均達到了1.8~2.2 cm,該精度基本上已經達到了水庫水位監測需求。
4 結束語
GNSS-IR高度差反演方法為水庫水位的監測提供了一種新的低成本手段。該方法不需要額外人工成本即可實現高時間分辨的水位監測,經過雙王城水庫數據的驗證,表明該方法的監測精度可以達到2 cm,與人工監測相比,不僅可以降低人工成本,還可以通過多系統、多測站的方式獲取高時間分辨率的水位結果,可以作為已建GNSS測站的內陸儲水設施的水位監測備選手段。另外,通過進一步分析表明,同一測站之間的不同頻率得到的水位結果存在系統偏差,且同時伴有隨高度差變化的線性誤差,需要在GNSS-IR技術用于傳統潮位監測的方法添加線性誤差和頻系統誤差改正。不同的頻間線性誤差系數也表明多頻融合的方法不能忽略該誤差對融合的影響。

