編碼計算研究綜述
鄭騰飛 周桐慶 蔡志平 吳虹佳
(國防科技大學計算機學院 長沙 410073)
隨著機器學習和大數據分析應用的涌現,相關數據集規模不斷增長,分布式地執行應用的計算任務可有效整合資源、緩解計算壓力.然而,分布式計算所需的頻繁數據洗牌常導致較高的通信負載,等待計算速度緩慢或發生故障節點的響應還會引入計算延遲,而節點的可信問題進一步制約著分布式計算范式的應用和發展.
近年來,研究人員將編碼理論應用到分布式計算領域,提出了一種新的計算框架——編碼計算(code computing, CC),旨在借助靈活多樣的編碼技術,降低通信負載,緩解計算延遲,并抵抗系統中的拜占庭攻擊,保護數據隱私.例如,文獻[1]通過對分布式計算任務的中間結果進行異或編碼,減少工作節點之間需要傳輸的信息數量和大小,以此顯著減少通信負載.在另一個例子中,文獻[2]利用糾刪碼對工作節點的任務進行編碼,使得主節點能夠從部分完成任務的節點中恢復最終結果,從而減少計算延遲.
鑒于其在通信、存儲和計算復雜度等方面的優勢,編碼計算一經提出便引起研究人員的廣泛關注,逐漸成為支撐有效分布式計算的熱門研究方向.當前編碼計算方案種類繁多、編碼形式多樣,有必要對當前方案進行總結和分析,以此為分布式計算、高性能計算、安全計算以及分布式機器學習、聯邦學習的研究人員提供啟發和思考.我們將本文和當前相關綜述文獻覆蓋的編碼方案進行了對比,如表1所示:

Table 1 Comparison of Existing Reviews on Coded Computing表1 已有編碼計算相關綜述文獻對比
其中,文獻[3]總結了利用編碼技術改進分布式機器學習性能的研究進展,缺少對基于編碼計算解決通信和安全隱私問題的總結和評述.同時,除分布式機器學習之外,在其他分布式計算場景中(例如,無線分布式網絡、異構分布式網絡、邊緣計算網絡)編碼計算技術面臨的挑戰也不盡相同,本文結合技術分析對編碼計算在多場景下的使用進行挖掘分析.另一方面,文獻[4]的綜述內容局限于對相關領域內一部分工作的細化闡述,缺乏對編碼計算相關技術進展的細粒度對比和解析,參考價值有限.為滿足分布式計算研究者靈活運用編碼計算技術,構建更為實用的分布式計算應用(例如聯邦遷移學習),尚且需要對涉及多場景,多類問題的編碼計算架構與技術予以全面綜述.
本文貢獻為:據作者所知,本文首次相對全面地總結了編碼計算的當前研究進展.首先,對編碼計算的基本原理進行介紹,并對現有編碼計算方案進行分類.根據不同的應用目標,本文將編碼計算方案分為面向通信瓶頸、面向計算延遲、面向安全隱私3類.進一步,分別從這3個方向對現有編碼計算方案進行了綜述,重點包括:1)介紹分析了Master-Worker架構下的面向通信瓶頸的編碼計算方案;2)根據不同的計算任務(矩陣乘法、梯度下降等),分別對面向計算延遲的編碼計算方案進行了討論和總結;3)從對抗惡意節點和防止數據泄露2方面分析總結了編碼計算在分布式計算安全和隱私方向的研究進展.
1 編碼計算概述
1.1 問題分析
分布式計算相關技術和理念已經在各種應用和場景中得以運用,然而,當在大量節點上分布式執行計算任務時,分布式計算系統將面臨3個挑戰:
1) 數據洗牌帶來的通信瓶頸.數據洗牌是分布式計算系統的核心步驟,其目的是在分布式計算節點之間交換中間值或原始數據.例如,在MapReduce架構中,數據從Mapper被傳輸到Reducer.通過對Facebook的Hadoop架構進行追蹤分析,平均有33%的作業執行時間都花費在數據洗牌上[5].在TeraSort,WordCount,RankedInvertedIndex和SelfJoin等應用程序中,50%~70%的執行時間用于數據洗牌[6].然而,在每一次數據洗牌過程中,整個數據集都通過網絡進行通信.頻繁數據交互帶來的通信開銷造成了分布式計算系統的性能瓶頸.
2) 掉隊節點帶來的計算延遲.分布式計算系統由大量計算節點執行計算任務,其中一部分工作節點的計算速度可能比平均速度慢5~8倍,甚至會出現未知故障[7],這類節點被稱為“掉隊節點(straggler)”.等待掉隊節點的反饋會給整個計算任務造成不可預測的延遲[8],降低系統性能.
3) 安全和隱私.計算分布引入的另一個重要問題是計算/工作節點存在不可控,不可靠等問題.與傳統集中式計算不同,分布式計算中的工作節點很可能是多個所有人的資產,這就使得數據輸入到系統后訪問面被動增加,導致數據的隱私受到威脅.例如,將涉及到用戶個人健康情況的醫療數據分發到多個節點可能會造成隱私泄露.與此同時,拜占庭攻擊是分布式系統面臨的一個傳統的安全威脅,節點提交錯誤信息將誤導最終的計算結果,極大地影響系統可用性.
1.2 編碼計算方案分類
由1.1分析可知分布式計算系統主要面臨3個方面的挑戰:1)數據洗牌帶來的通信瓶頸;2)掉隊節點造成的不可預測的延遲;3)系統安全和數據隱私.這三者嚴重制約著系統的擴展性和服務性能.為應對上述挑戰,研究人員提出了一系列編碼計算方案.根據各方案的主要功能和目標,可以相應地將編碼計算方案分為3類:
1) 優化通信負載編碼.以降低分布式計算系統的通信開銷.優化通信負載編碼方案通過增加額外的計算操作,創建編碼機會,從而減少數據洗牌所需的通信負載.文獻[1]是該方向的第一篇研究,其在分布式計算負載和通信負載之間實現了逆線性平衡——將計算負載增加r倍(即在r個節點上計算每個任務),則可以將通信負載降低r倍.隨后,文獻[9-12]將文獻[1]方案分別擴展到無線分布式網絡,多階段數據流應用程序,計算任務密集型分布式系統和異構分布式網絡中,有效降低了不同分布式計算場景下的通信負載.Attia等人[13]提出了一種用于分布式機器學習的近乎最佳的編碼數據洗牌方案,得到工作節點不同存儲方式下通信開銷的最優下界.Li等人[14]提出了一種壓縮編碼分布式計算方案,相比于文獻[1]方案進一步降低了分布式計算系統中的通信負載.Song等人[15]對索引編碼方案[11]進行修改,并在此基礎上提出了一種用于分布式計算系統的半隨機柔韌性索引編碼數據洗牌方案,該方案平均能節省87%的傳輸開銷.
2) 最小化計算延遲編碼.以減輕分布式計算系統的掉隊節點導致的延遲弊端.最小化計算延遲編碼計算方案能夠在計算負載和計算延遲(即整個作業響應時間)之間進行逆線性平衡.換言之,該方向的編碼計算方案利用編碼來有效地注入冗余計算,以此來減輕掉隊節點的影響,并通過注入與冗余量成比例的乘法因子來加速計算.Lee等人[2]利用最大距離可分碼(maximum distance separable code, MDS碼)首次解決分布式矩陣-向量乘法中的延遲問題,并且降低了分布式機器學習算法中數據洗牌的通信成本.和文獻[2]目標一致,文獻[16-18]分別提出了不同的編碼計算方案,以降低分布式矩陣-向量乘法中的計算延遲.除此之外,針對其他分布式計算任務如矩陣-矩陣乘法[19-23]、梯度下降[24-29]、卷積計算、傅里葉轉換[30-31]和非線性計算[32]等中的計算延遲,研究人員也提出了相應的編碼計算方案.
為了處理異構分布式計算系統中的掉隊節點,必須考慮到為異構節點設計負載平衡策略[33-38],以最大程度地減少總體作業執行時間.考慮到分布式計算系統中掉隊節點的動態性,如何有效地利用掉隊節點所做的計算結果優化計算延遲也引起了研究人員的廣泛關注[39-43].
3) 安全和隱私編碼.為分布式計算系統提供安全的計算過程.為抵抗梯度下降中的拜占庭攻擊,Chen等人[44]利用編碼理論的思想提出了DRACO編碼計算方案.Gupta等人[45]利用“響應冗余”,可在梯度聚合時檢測出計算錯誤的節點.Data等人[46]通過對數據進行編碼,基于錯誤校正[47]設計了一種抗拜占庭攻擊的分布式優化算法.Yu等人[48]提出一種拉格朗日編碼計算(Lagrange coded computing, LCC)方案,該方案對輸入數據進行編碼,不僅可以減少計算延遲,而且可以抵抗惡意節點的攻擊,保護數據隱私.作為LCC的擴展,So等人[49]提出了一種快速且具有隱私保護功能的分布式機器學習框架——CodedPrivateML. Nodehi等人[50]將多項式碼與BGW方案[51]結合在一起,提出了一種多項式共享方案.隨后,針對矩陣乘法,研究人員分別提出了單邊隱私[52-54]和雙邊隱私[55-58]的編碼計算方案.文獻[59]針對邊緣計算架構中源節點、工作節點、主節點不同的隱私需求設計了相應的編碼計算方案.
表2按照分類思路列出了代表性工作,將在第3~5節詳細介紹,分析各分類的典型工作.

Table 2 Classification of Coded Computing Schemes表2 編碼計算方案分類
1.3 編碼計算定義
編碼計算目前還未有一個嚴格的統一的定義,為簡要說明編碼計算的思想,列舉2個示例:
示例1.降低通信負載編碼[2].假設一個分布式計算系統具有2個工作節點和1個主節點,現有一個大數據矩陣被分為4個子矩陣,即A1,A2,A3,A4,分別存儲在節點W1和W2中,如圖1(a)所示.其目標是主節點將A3傳輸至W1,并將A2傳輸至W2.可以設計這樣一種編碼,使主節點發送多播編碼信息A2+A3到2個工作節點,后者使用本地已存儲的數據便可解碼獲得所需的數據.顯然,與未編碼的數據洗牌方案相比,編碼方案可降低50%的通信開銷.
示例2.減少計算延遲編碼[2].接下來考慮另一個簡單例子,圖1(b)展示一個具有3個工作節點和1個主節點的分布式計算系統,其目標是計算矩陣乘法AX,其中A∈q×r,X∈q×r.數據矩陣A被劃分為A1和A2兩個子矩陣.可以這樣設計編碼,在進行計算任務分配前,由主節點對子矩陣進行編碼生成數據A3=A1+A2.而后,主節點將A1,A2,A3分別分配給W1,W2,W3.當工作節點接收到矩陣X時,每個節點將X與存儲的數據相乘,并將計算結果返回給主節點.通過觀察可知,主節點在接收到任意2個工作節點的結果時都可以恢復最終結果AX,而不用等待最慢的節點(掉隊節點)響應.

Fig. 1 Simple example of coded computing圖1 編碼計算簡單示例
值得注意的是,示例1為了在傳輸數據時可以進行編碼,引入了冗余,即節點W1和W2分別額外存儲了數據A2和A4.示例2同樣引入了冗余——給W3分配了額外的計算任務(A1+A2)X,以此使得分布式計算系統可以容忍1個掉隊節點的存在.由此可見,編碼計算的核心思想是注入并充分利用分布式計算系統中的數據或計算冗余.本文將編碼計算定義如下:編碼計算是利用編碼理論注入冗余,通過對存儲-通信-計算的權衡,從而解決或緩解分布式計算系統中通信瓶頸,計算延遲,安全和隱私等問題的一系列技術手段.
2 面向通信瓶頸的編碼計算
近年來,研究人員對Master-Worker分布式計算架構下的數據洗牌問題進行了大量研究.其中根據主節點是否參與運算及存儲數據,Master-Worker架構可分為Map-Reduce和典型Master-Worker兩種略有區別的分布式計算架構.而在這2種不同分布式計算架構下的數據洗牌編碼方案也不盡相同.因此,在第2.1和2.2節,將分別對基于Map-Reduce和典型Master-Worker的數據洗牌編碼計算方案進行介紹和分析.
2.1 基于Map-Reduce的數據洗牌編碼計算
MapReduce是一種編程范式,可以并行處理海量數據集.在MapReduce架構中,主節點不參與運算,且不存儲數據,只為各工作節點協調分配不同的輸入數據.更具體地說,在MapReduce中整個計算被分解為“Map”,“Shuffle”和“Reduce”3個階段.在Map階段,工作節點根據設計的Map函數使用輸入數據來計算中間值的一部分;在Shuffle階段,工作節點相互交換一組中間值;在Reduce階段,工作節點計算并輸出最終結果.針對Map-Reduce架構,研究人員通過將子數據集映射到多個工作節點,并仔細設計放置策略,以創建編碼機會.編碼計算利用該機會將各工作節點計算的中間值進行異或編碼,然后將編碼信息廣播給其他工作節點,以此降低通信負載.
2.1.1 通用數據洗牌編碼方案
針對Map-Reduce架構,Li等人[1]提出了編碼分布式計算(coded distributed computing, CDC)方案,并在后續工作中將CDC方案擴展到無線分布式計算系統[9]、多級數據流[10]和TeraSort排序算法[61]等.這里結合圖2所示計算用例概述CDC方案的基本思路.
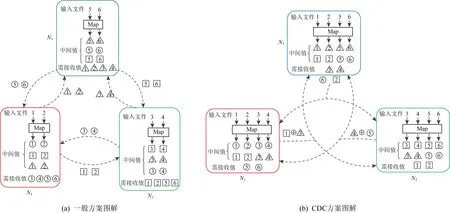
Fig. 2 Data shuffling between general scheme and CDC圖2 一般方案和CDC方案數據洗牌對比
假設客戶端需從6個輸入文件中計算3個輸出函數,分別用圓形、正方形和三角形表示,計算任務由節點N1,N2和N3協同完成.每個節點計算唯一的輸出函數,例如N1計算圓形函數,N2計算方形函數,N3計算三角形函數.
在計算上不加冗余時,如圖2(a)所示,如果每個節點在本地存儲2個輸入文件,這樣便可在本地生成6個所需的中間值中的2個.因此,每個節點需要從其他節點接收另外4個中間值,產生的通信負載為4×3=12.
如圖2(b)所示,CDC使每個輸入文件映射到2個節點.顯然,由于執行了更多的本地計算任務,因此每個節點現在僅需要2個其他中間值,此時的通信負載為2×3=6.由于每個節點計算出了更多的中間值,因此在數據洗牌時便有了編碼的機會.CDC將每個節點處生成的2個中間值進行異或編碼,并多播到另外2個節點,此時的通信負載為3.因此,CDC產生的通信負載比沒有計算冗余的情況下的通信負載降低了4倍,比未編碼的數據洗牌方案低2倍.可見,這樣以計算換通信的方式可有效降低洗牌時的傳輸開銷.隨后,文獻[1]從數據映射、計算、數據洗牌和歸約4個階段對CDC的一般化過程進行了形式化定義.
CDC關注的是由MapReduce驅動的通用框架中的通信流,并且適用于任意數量的輸出結果、輸入數據文件和計算節點,不要求計算函數具備任何特殊性質(如線性).
2.1.2 有領域知識的數據洗牌編碼方案
Li等人[9]將CDC方案推廣到無線分布式計算系統,設計了一種無線分布式編碼計算(coded wireless distributed computing, CWDC)的框架.CWDC由上行鏈路和下行鏈路2部分組成,每個用戶在上行鏈路發送2個中間值的異或值至接入點,如圖3(a)所示.然后接入點無需解碼任何單獨的值,只需生成接收到的消息的2個隨機線性組合C1(·,·,·)和C2(·,·,·),并將它們廣播給用戶,即可同時滿足所有的數據請求,如圖3(b)所示.圖示編碼方法中上行鏈路通信負載為3,下行鏈路通信負載為2.
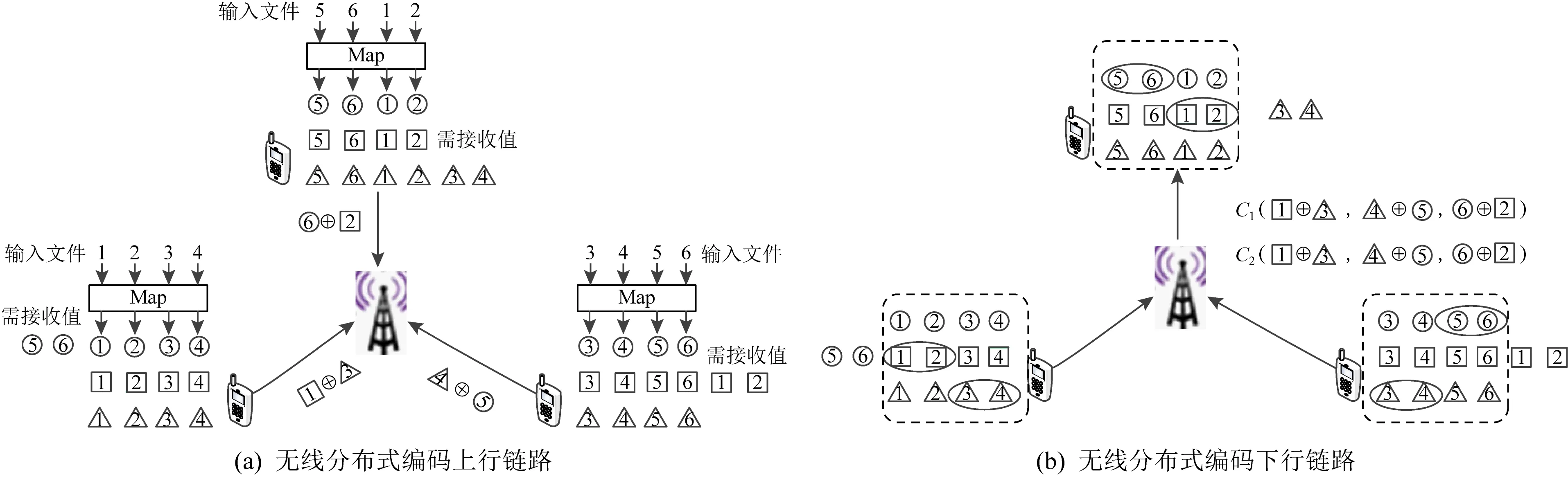
Fig. 3 The diagram of data shuffling in CWDC coded scheme圖3 CWDC編碼方案數據洗牌圖解
對于具有K個用戶的無線分布式計算應用程序,假設每個工作節點可以存儲整個數據集的μ(0<μ≤1)倍,所提出的CWDC方案的通信負載為

(1)
與未編碼方案相比,CWDC可將通信負載降低μK倍,并且其通信負載是固定的和工作節點數量無關.
許多分布式計算應用程序包含多個MapReduce階段.例如機器學習算法[62]、數據庫SQL查詢[63-64]和數據分析[65].基于此,Li等人[10]為多階段數據流應用程序形式化定義了分布式計算模型.其將多級數據流表示為一個分層的有向無環圖(directed acyclic graph, DAG),在這個DAG中,每個頂點代表一個MapReduce類型計算,方案通過對每個頂點實施CDC編碼策略,有效降低通信負載.
CDC中的一個隱含假設是每個服務器對存儲在其內存中的所有文件執行所有可能的計算.然而,當工作節點需要執行計算密集型任務時,可能沒有足夠的時間來執行所有計算.針對這種情況,Ezzeldin等人[11]在CDC方案的基礎上提出了一種分割編碼計算(spilt coded distributed computing, S-CDC)方案.作者通過給定節點的計算能力閾值,從而得出相關通信負載的下限,并基于CDC提出一種啟發式方案,以達到該通信下限.
在文獻[61]中,作者將CDC的思路應用于Tera-Sort排序算法,并設計了一種名為CodedTeraSort的新分布式排序算法,該算法在數據中施加結構化冗余,以在數據洗牌階段創造有效的編碼機會.作者通過實驗評估了CodedTeraSort算法在Amazon EC2集群上的性能,與傳統的TeraSort相比,Coded-TeraSort速率高1.97~3.39倍.
2.1.3 線性假設下的數據洗牌編碼方案
在沒有進一步假設的情況下,CDC[1]實現了最優的計算和通信負載之間的平衡.然而,工作節點計算的函數通常有一些結構,利用這些結構可以進一步降低通信負載.
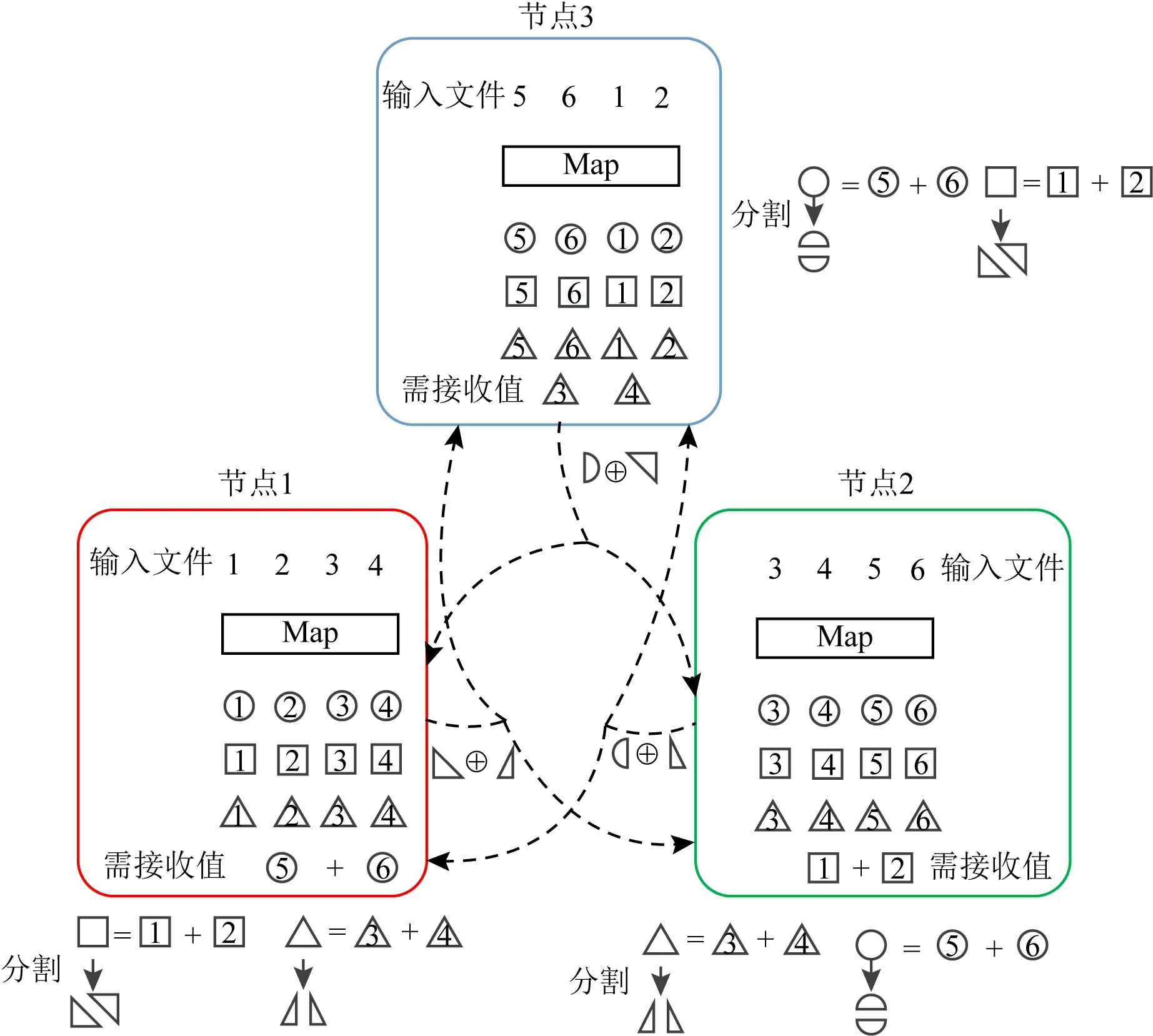
Fig. 4 The diagram of data shuffling in CCDC圖4 CCDC編碼方案數據洗牌圖解
在Reduce階段是線性聚合的假設下,Li等人[14]將壓縮技術和CDC相結合提出了一種壓縮編碼分布式計算(compressed coded distributed computing, CCDC)方案.考慮如圖4所示的分布式計算場景,假設最終計算結果是計算各中間值之和,則可以在發送節點上預先組合相同函數的中間值以減少通信.
例如,節點1將兩對中間值相加以生成2個分組,然后將每個分組(正方形和三角形)分割為2段,并取各自的一段逐位進行異或,以生成大小為中間值一半的編碼數據.最后,節點1將該編碼數據多播到節點2和3.節點2和3處執行類似的操作.
最后,每個節點可以利用本地已有的中間值來解碼獲得所需的數據.該編碼方案可用于需在最后階段對中間結果線性聚合的分布式機器學習中.
Horii等人[66]指出在Map階段計算的中間值可以看作是2中的向量.假設工作節點發送的向量數為r,由這些向量構造的線性子空間的維數可能小于r.例如,在計算大量文檔中的單詞數時,工作節點計算的許多中間值是相同的,并且中間值的一些線性組合也是相同的.Horii等人基于這個觀點和假設,在編碼時讓工作節點發送中間值的線性子空間的基和線性組合系數,從而進一步降低通信負載.
2.2 基于典型Master-Worker的數據洗牌編碼計算
與Map-Reduce架構不同,在典型Master-Worker計算框架中,主節點可以訪問整個數據庫,并且只有主節點可以發送數據,而各工作節點之間無法進行通信.主節點在每次迭代中將整個數據集排列劃分為多個子數據集,并將每個子數據集傳輸到相應的工作節點,以便工作節點執行本地計算任務.工作節點在完成計算后將結果返回給主節點.典型Master-Worker架構下的編碼計算方案可分為數據洗牌和存儲更新2個階段.在數據洗牌階段,主節點將整體數據分為大小相同的子數據集,并將子數據集的編碼信息廣播發送給工作節點,每個工作節點從主節點廣播的編碼信息和本地存儲的數據中恢復出下次迭代所需的數據.在存儲更新階段,每個工作節點存儲新分配的數據單元并更新存儲結構以實現下次迭代的數據洗牌.值得注意的是,在編碼計算方案中工作節點需額外存儲一些關于其他數據單元的信息.編碼計算將此類附加數據進行仔細設計,以幫助在下次迭代時從編碼信息中解碼所需數據.
Lee等人[2]首次提出了典型Master-Worker分布式計算架構下的編碼數據洗牌方案,旨在提高分布式機器學習算法的訓練速率.假設數據集一共有q個數據行,工作節點數為n,每次迭代時將數據集隨機均勻的分配給各個工作節點,則每個工作節點需要處理q/n個數據行.假設每個工作節點的內存大小為s(s>q/n)個數據行,由此可知工作節點在每次算法迭代時除了存儲計算任務所需的q/n個數據行外,還有額外s-q/n個數據行的存儲空間.文獻[2]充分利用這部分存儲空間,讓每個工作節點從剩余的數據行中隨機均勻的選擇s-q/n個數據行進行存儲,形成“側信息”.在數據洗牌時,主節點利用異或編碼的方式將數據集編碼,并將編碼信息廣播至各工作節點.各工作節點利用“側信息”完成解碼,獲取下次迭代所需數據.Lee等人通過實驗表明在n=50,q=1 000,s/q=0.1時,用于數據洗牌的通信開銷減少了81%.因此,在緩存的存儲開銷非常低的情況下,與未編碼方案相比可以顯著地降低分布式系統的通信開銷.
在給定一組數(K,N,S)(K為節點數,N為文件總數,S為每個節點的存儲大小)的情況下,Attia等人[67-68]刻畫了每個工作節點存儲容量與最大通信負載之間的關系.具體來說,在文獻[67]中,針對工作節點數K={2,3}的情況,Attia等人將最大通信負載描述為一個關于可用存儲的函數.在文獻[68]中,Attia等考慮了無多余存儲的情況(即,S=N/K),表明即使對于最小存儲值,編碼機會仍然存在.然而,該方案的參數不能取任意值.
隨后,Attia等人[13]在編碼緩存方案[69-70]的啟發下,提出了一種新穎的編碼數據洗牌方案,該方案基于一種保持存儲結構不變的存儲/更新過程,稱為“結構不變的放置和更新(structural invariant placement and update, SIP/SIU)”.
SIP/SIU和文獻[2]類似,工作節點除了存儲必要的處理數據外,需額外存儲一些附加數據,如圖5所示.和文獻[2]中隨機存儲分配不同,SIP/SIU以一種確定性和系統化的存儲更新策略創造了更多的編碼機會.
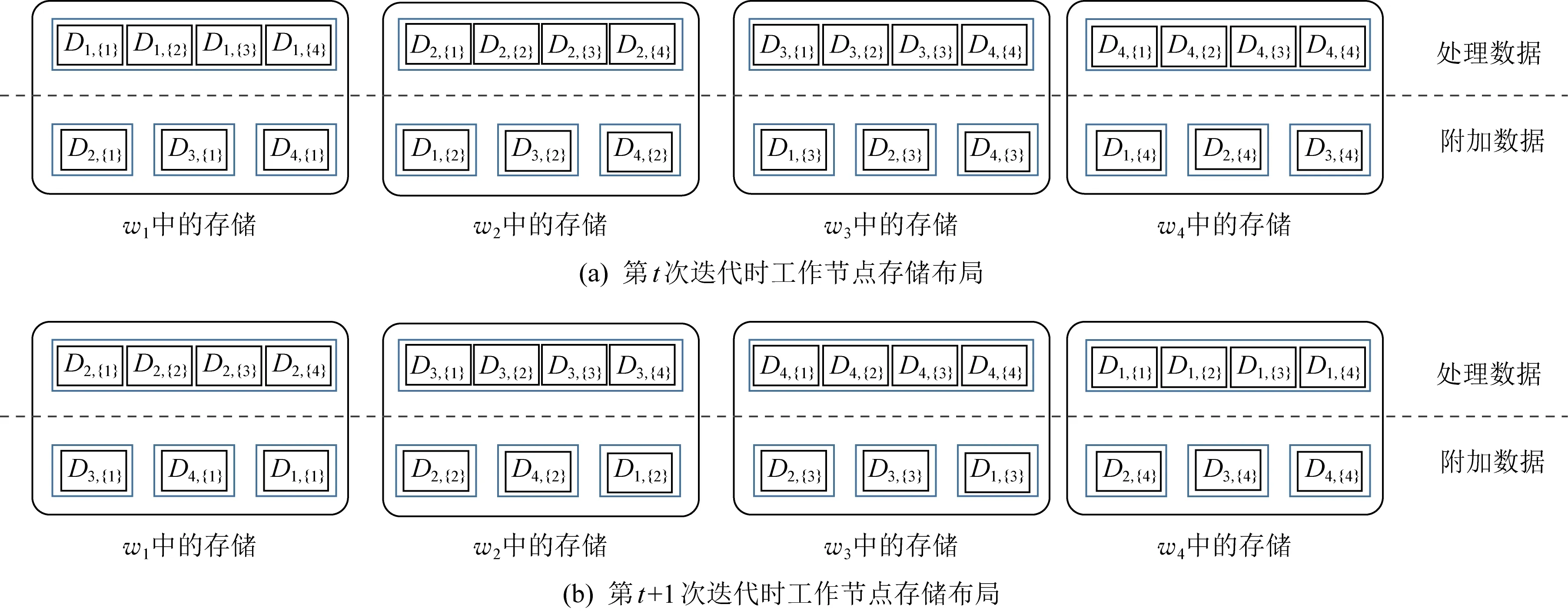
Fig. 5 Storage of work nodes in SIP/SIU圖5 SIP/SIU方案中工作節點的存儲布局
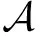

(2)

Fig. 6 Storage of work nodes and the processes of storage update in [71]圖6 文獻[71]中工作節點存儲布局及更新過程
Attia等人通過數值模擬實驗表明,對于具有較大存儲容量工作節點的分布式計算系統,文獻[13]要優于文獻[2]中的編碼方案,并且具有較低的計算復雜度.
Elmahdy等人[71]基于SIP/SIU方案提出了一種不同的編碼洗牌方案,并證明了當文件數等于工作節點數時,其編碼數據洗牌方案是最優的.以K=4(w1,w2,w3,w4)個工作節點的分布式計算系統為例,簡要說明該方案.設有4個輸入文件N=4,分別命名為A,B,C,D,每個工作節點的內存大小為S=2個文件.不失一般性,假設w1,w2,w3,w4在第t次迭代時正在處理的文件分別為A,B,C,D.
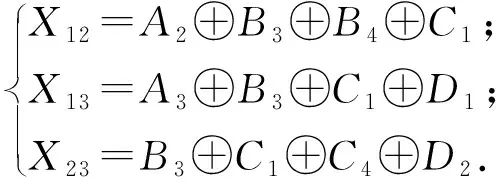
(3)
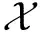
由分析可知,每次迭代時主節點需發送3個子消息,假設每個子消息的大小為1/3,則文獻[71]所提出方案的通信負載為1.在相同的內存布局策略下,非編碼洗牌方案需發送8個子消息,最終的通信負載為8/3.因此,在該場景下,與非編碼洗牌方案相比,Elmahdy等人所提出的編碼洗牌方案可節省約62%的通信負載.
“好”的數據洗牌方案需要緩存的數據在各工作節點之間和算法迭代過程中具有足夠的差異[72-74],受這一想法的激勵,Li等人[15]提出了一種受約束的柔韌性索引編碼數據洗牌方案,該方案在通信成本和計算性能之間取得了平衡.
為了達到該目的,Li等人在索引編碼方案的基礎上做了2項修改:1)添加一條約束,即一條消息最多可以發送給c個工作節點,以確保只有一小部分工作節點可以緩存同一條消息.該約束旨在降低工作節點間消息的相關性,確保工作節點間緩存內容的差異足夠大.2)設計了一個分層結構,即將消息分成組,在迭代過程中,每個工作節點只緩存特定的消息.該修改旨在降低迭代過程中消息的相關性,以確保迭代過程中各工作節點緩存內容的差異足夠大.通過在一個真實數據集上進行實驗,與基于索引編碼的替換式隨機洗牌方案[2]相比,文獻[15]提出的方案平均能減少87%的傳輸消耗.
2.3 小 結
本節我們總結了Master-Worker架構下2種不同分布式計算框架中優化通信負載的編碼計算方案.首先我們對此類方案進行總結和回顧,如表3所示:
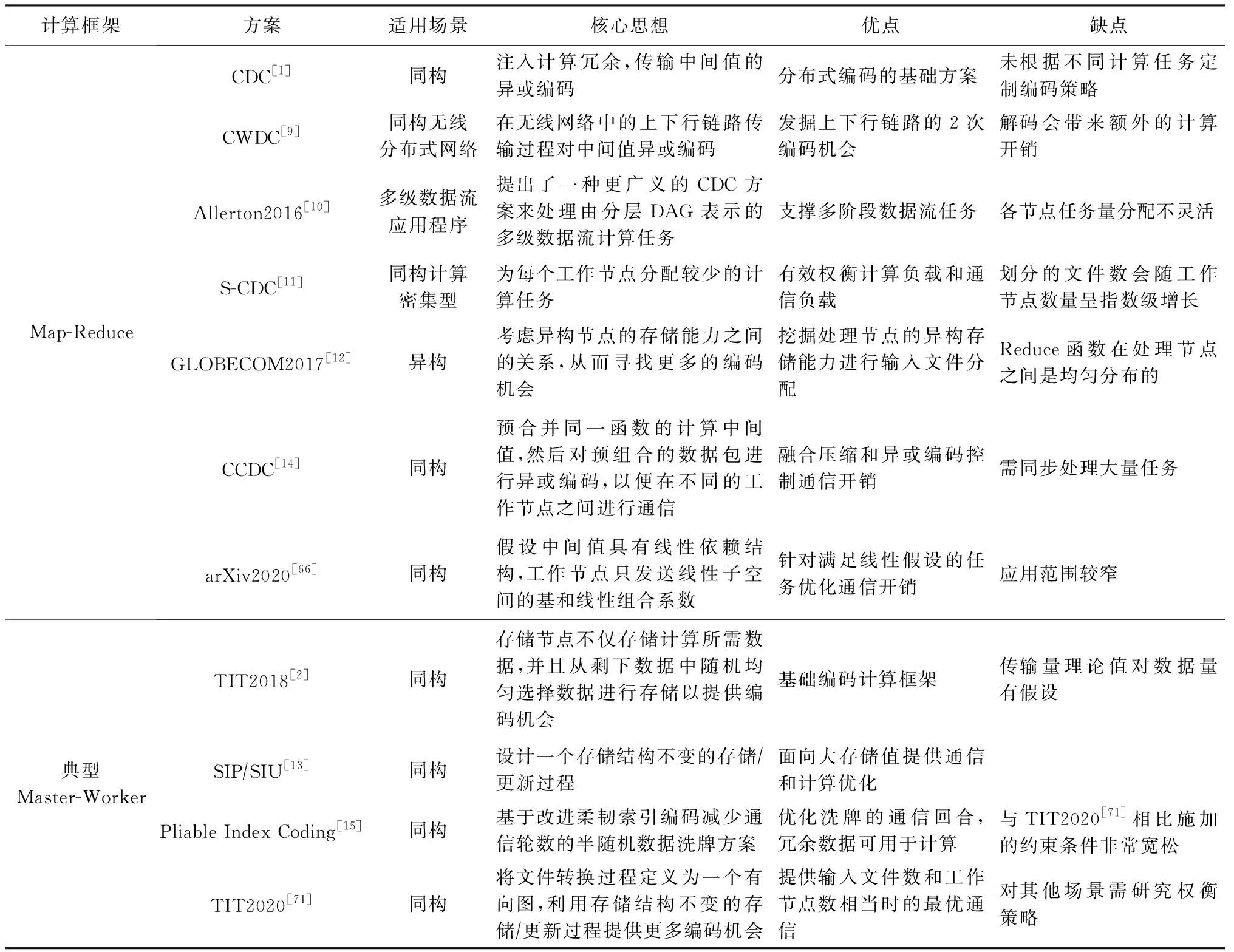
Table 3 Summary and Review of Coded Computing Schemes for Communication Bottleneck表3 面向通信瓶頸的編碼計算方案總結與回顧
在Map-Reduce架構下的編碼計算方案通過將輸入數據映射到多個工作節點,并精心設計分配策略,從而創造編碼機會.而在不注入計算冗余的情況下,工作節點交換中間值時,由于沒有解碼所需的信息,所以不能對中間值進行編碼.通過注入冗余,CDC[1],CodedTeraSort[61]可以將中間值進行異或編碼;CWDC[9]可以在無線分布式網絡上下行鏈路分別將中間值異或編碼和線性組合編碼;CCDC[14]在Reduce函數是線性相關的假設下,可以對中間值進行壓縮,然后異或編碼;文獻[66]則在中間值具有線性相關性假設下,可以只交換編碼信息的線性子空間的基和線性組合系數,但其在編碼階段需要更多的計算開銷;文獻[11-12]則分別是CDC方案在多級數據流應用和異構分布式系統下的推廣,其考慮了更多的約束條件,但編碼思想和方式與CDC方案相同.
與Map-Reduce架構在數據洗牌階段傳輸計算結果信息不同,在典型的Master-Worker架構中數據洗牌階段需傳輸原始數據.對此類方案分析可知,典型Master-Worker架構中工作節點存儲計算任務所需的數據外,還需存儲一些“冗余數據”.正是因為引入了存儲冗余,所以數據洗牌階段才有編碼機會.因此典型Master-Worker架構中編碼洗牌方案的通信負載和各節點多余存儲空間大小相關.一個極端的情況是,當所有的工作節點都有足夠的存儲空間來存儲整個數據集時,數據洗牌階段不需要通信.而另一個極端情況,當所有工作節點的存儲空間剛好足以存儲任務所需的數據時(稱為無多余存儲空間的情況),則通信量將達到最大.文獻[2,13,71]考慮了無替換的數據洗牌,即附加數據用于提高通信效率,而不用于計算.然而,當額外的存儲數據用于計算時,可以獲得潛在的計算增益.例如,為了訓練分類器模型,額外存儲的數據樣本也有助于模型訓練.
通過對面向通信瓶頸的編碼計算方案的分析可知,編碼計算可以有效降低數據洗牌階段的通信負載.然而,通信負載的降低通常以更大的計算負載和更大的存儲為代價.因此,需要權衡計算-存儲-通信三者之間的關系,才能更好地評估方案的性能.
3 面向計算延遲的編碼計算
面向計算延遲的編碼計算方案的核心思想是通過使用編碼技術,創建任務冗余,即在更多的工作節點上分配計算任務,使得主節點在不接收掉隊節點結果的情況下依然可以恢復最終結果.在面向計算延遲的編碼計算方案中,一個重要的性能指標是恢復閾值,它是指在最壞情況下,主節點解碼最終結果需要等待的工作節點的數量[2].一般來說恢復閾值越小,完成最終任務需等待完成計算的工作節點的個數越少,計算延遲越短.面向計算延遲的編碼計算方案的目標是降低恢復閾值,以便通過等待較少的工作節點來恢復最終結果,從而減少計算延遲.
為了降低不同分布式計算任務的計算延遲,可以利用具體運算的代數結構來設計編碼方案.在隨后章節,本文將介紹分析當前編碼計算方案在不同計算任務中的應用.除此之外,本文還將簡單討論研究人員在異構場景和利用掉隊節點結果等方面所提出的編碼計算方案.
3.1 面向矩陣乘法運算的編碼計算
3.1.1 矩陣-向量乘法
分布式矩陣-向量乘法是線性變換的組成部分,是機器學習和信號處理應用中的一個重要步驟.為方便方案描述,首先定義分布式計算矩陣-向量乘法系統,該系統具有1個主節點和P個工作節點,其目標是分布式計算大小為m×n的矩陣A和n×1的向量x的積:b=Ax.如無特殊說明外,本節編碼計算方案的計算場景和目標遵循該定義.我們將對不同的編碼方案進行簡要介紹和分析.
1) MDS編碼方案.與簡單的將同一個計算任務分配給多個工作節點(重復編碼)不同,Lee等人[2]利用MDS碼來克服矩陣-向量乘法中的計算延遲問題.基于MDS碼的方案的編碼策略是首先將矩陣A按列劃分為k個子矩陣,每個子矩陣的大小為m×n/k.隨后使用(P,k)MDS碼對k個子矩陣進行編碼,從而生成P個編碼子矩陣.隨后將編碼子矩陣發送至工作節點,工作節點計算編碼子矩陣與向量x的積,并返回主節點.則主節點可以根據最快的k個計算節點恢復出最終結果b.如1.3節圖1(b)所示,為一個使用(3,2)MDS碼的編碼計算方案實例.
2) Short-Dot.在基于重復編碼或者MDS碼的編碼計算方案中,每個工作節點需計算長度為n的點積,而Dutta等人[16]認為通過縮短點積的長度,可以減少工作節點的計算時間.因此Dutta等人提出了一種“短點積”(short-dot)的編碼計算方案,該方案通過對子矩陣施加稀疏性以使工作節點計算較短的點積.然而,工作節點計算點積的長度越短,該方案的恢復閾值越高.
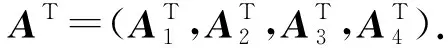
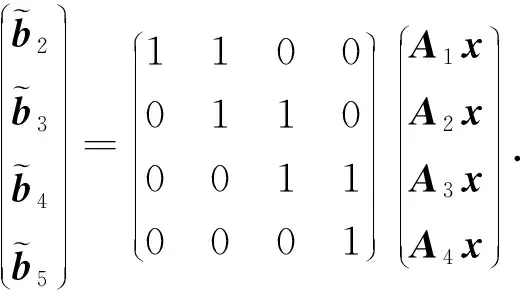
(4)
由式(4)可知,系數組成的矩陣為上三角矩陣,由于主對角線中的元素是非0的,所以它是可逆的.因此可以通過求系數矩陣的逆來恢復最終結果.利用對角線結構,s-對角線編碼方案不僅降低了計算負載,并且可以實現和文獻[2]相同的恢復閾值.
4) 無碼率編碼.LT碼[75]是一類用于從有限的源符號集生成無限多個編碼符號的糾刪碼.Mallick等人[18]通過將矩陣A的m行視為源符號,將LT碼用于矩陣-向量乘法.該方案首先根據Robust Soliton度分布選擇參數d,隨后從A中隨機均勻的選擇d個數據行并將它們隨機相加生成編碼行.即d決定了每個編碼行中的原始數據行的數量.原數據行與編碼數據行之間的映射對于成功解碼至關重要,因此,此映射需存儲在主節點上.
假設對m個原始數據行進行編碼生成了αm個編碼行,則主節點將αm個編碼行平均分配給P個工作節點.工作節點計算編碼行和向量x的乘積,并將結果返回給主節點.如果一個工作節點在主節點能夠解碼b之前完成了分配給它的所有向量積,則它將保持空閑狀態,主節點繼續從其他工作節點收集更多的行向量積.一旦主節點獲得了足夠的結果可以解碼b=Ax,則它將向所有工作節點發送完成信號以停止計算.和其他方案相比,無碼率編碼方案可以實現理想的負載平衡并且具有較低的解碼復雜度.
3.1.2 矩陣-矩陣乘法
矩陣乘法是許多數據分析應用程序中關鍵操作之一.此類應用程序需要處理TB級甚至PB級的數據,這需要大量計算和存儲資源,而單臺計算機通常無法滿足.因此,在大型分布式系統上部署矩陣乘法計算任務已經引起了廣泛的研究[76-77].
本文首先定義分布式矩陣乘法計算場景.該分布式計算系統有一個主節點和N個工作節點(w1,w2,…,wN)組成,其目標是計算大矩陣乘法C=ATB.其中A∈r×q,B∈r×s.為了分布式計算該矩陣乘法,首先將2個輸入矩陣分別(任意)劃分為p×m和p×n個子矩陣塊,其中同一輸入矩陣內的所有子矩陣大小相等.然后將A,B中每個子矩陣分配給各工作節點,工作節點完成計算任務后,將計算結果返回給主節點.主節點恢復最終結果輸出C=ATB.如無特殊說明外,本節編碼計算方案的計算場景和目標遵循該定義.我們將對不同的編碼方案進行簡要介紹和分析.
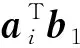
2) 乘積碼.隨后Lee等人基于乘積碼[78],在文獻[19]中提出了另一種新穎的編碼矩陣乘法方案,該方案較1D-MDS編碼方案具有更低的恢復閾值.乘積碼是用小編碼塊作為構建塊構建較大編碼塊的一種方法.以N=9,m=n=2,p=1為例,簡要說明乘積碼的編碼解碼過程.由于m=n=2,因此有:
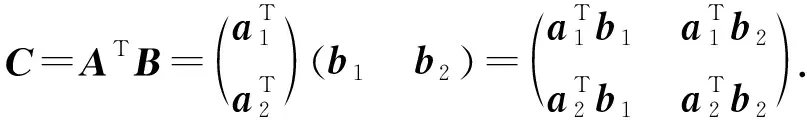
(5)
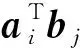
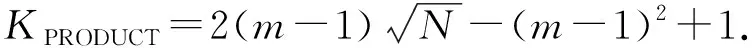
(6)
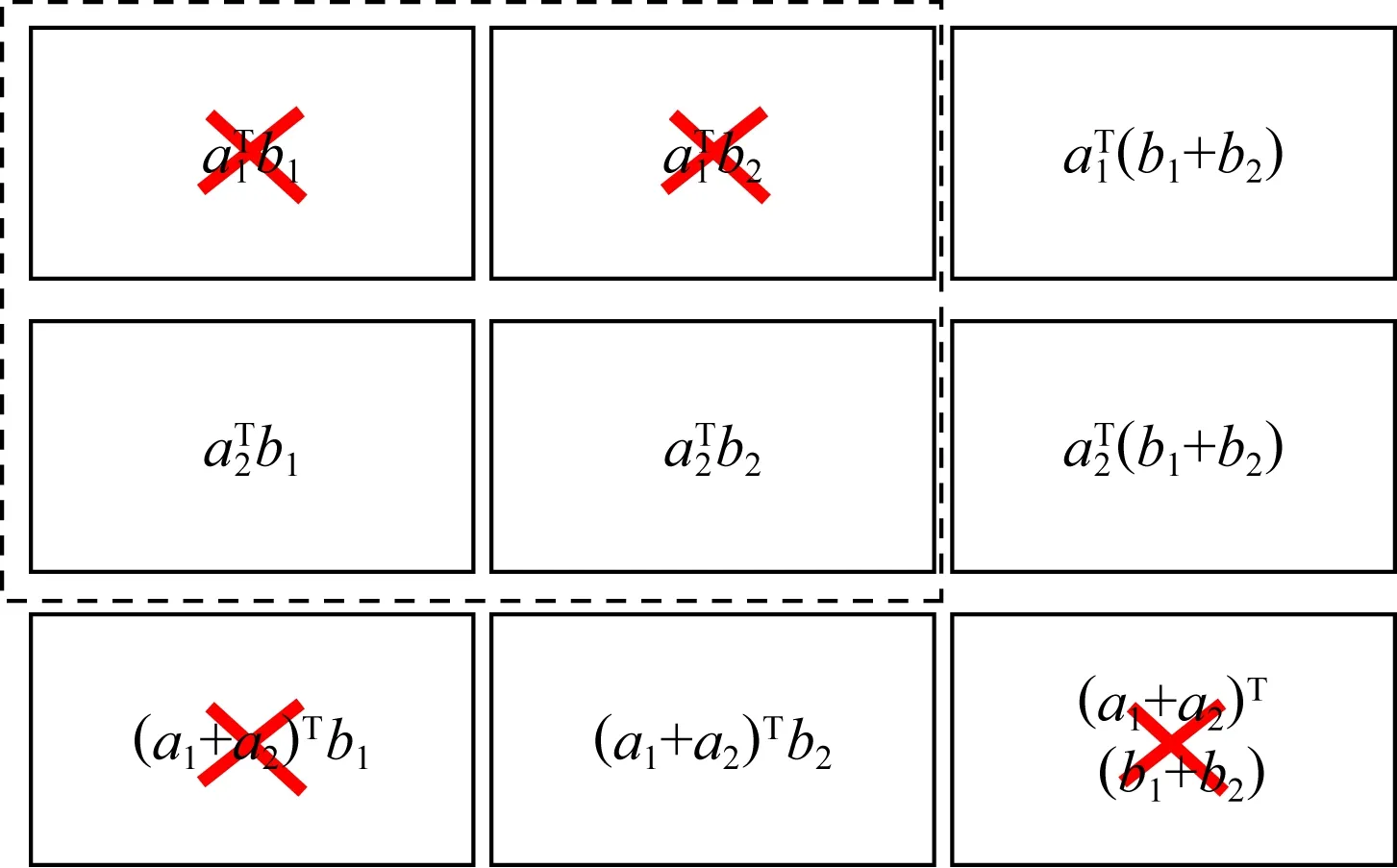
Fig. 7 An example of computing tasks assignment圖7 計算任務分配示例
介紹一類以多項式碼為基礎的編碼計算方案[20-22],這類方案的共同特征是為每個工作節點分配不同的隨機數,并使用該隨機數對輸入矩陣進行編碼,從而使得最后解碼過程可視為多項式插值問題,不同之處在于各方案對輸入矩陣的切割方式不同.基于多項式碼的編碼計算方案的主要優點是可實現最佳恢復閾值,且恢復閾值不隨工作節點的數量的變化而變化.
3) 多項式碼.為了尋找最佳恢復閾值,Yu等人[20]提出了一種基于多項式碼的編碼計算方案,該方案的恢復閾值與工作節點數量無關,且遠小于MDS碼和乘積碼方案中的恢復閾值.為構造多項式編碼計算方案,Yu等人首先將輸入矩陣A和B沿垂直方向分別劃分為m和n個子矩陣,即A=(A0,A1,…,Am-1),B=(B0,B1,…,Bn-1).隨后隨機分配給每個工作節點wi一個互不相同的數,記為xi∈q(q為一個足夠大的有限域).對于給定的參數α,β∈,Yu等人定義如下(α,β)-多項式碼:對?i∈{0,1,…,N-1},計算:
(7)
(8)
(9)
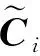
(10)
4) MatDot.由文獻[20]可知,當m=n時,多項式碼方案的恢復閾值為m2.針對m=n的情況,Fahim等人[21]提出了一種恢復閾值更低的編碼計算方案,稱為“MatDot”.MatDot假設矩陣A和B都為P×P的方陣,并將兩矩陣分別在垂直和水平方向劃分為m個大小相等子矩陣.其編碼思想和多項式編碼[20]相似,在m=n時,MatDot方案的恢復閾值為KMatDot=2m-1,其遠遠小于多項式編碼的恢復閾值m2.
5) PolyDot.雖然MatDot的恢復閾值比多項式碼方案[20]低,但在通信成本方面,MatDot中每個工作節點的通信成本為O(N2),要比多項式碼方案的通信成本O(N2/m2)高.因此Fahim等人[21]針對矩陣A和B都是方陣的情況,在MatDot的基礎上提出了一種名為“PolyDot”的編碼方案.該方案權衡了恢復閾值和通信成本之間的關系,是MatDot和多項式碼[20]方案的折中.一般而言,PolyDot的恢復閾值為KPolyDot=t2(2s-1)(st=m),通信成本為O(N2/t2).
6) 糾纏多項式碼.與只允許將矩陣按列劃分的多項式碼方案不同,Yu等人[22]在多項式碼方案的基礎上提出了一種名為糾纏多項式碼的編碼計算方案.該方案允許對輸入矩陣進行任意劃分.在糾纏多項式編碼方案中,矩陣A和B分別被分割為p×m和p×n個子矩陣塊,其中同一矩陣內的所有子矩陣大小相等.換句話說,多項式碼方案[20]是p=1的特殊情況.
通過選擇參數p,m和n不同的值,糾纏多項式碼可以實現系統資源的不同利用,從而平衡存儲和通信成本.該方案的恢復閾值為KEntangled polynomial=pmn+p-1.此外,糾纏多項式碼啟發了通用多項式計算[48]、安全/私有計算[79]和區塊鏈系統[80]中編碼計算方案的發展.
7) 稀疏編碼.大規模機器學習中許多問題都表現出極大規模的稀疏性,編碼方案可能會破壞這種稀疏結構,并且導致更高的計算開銷.Wang等人[23]通過實驗證明,在稀疏矩陣乘法中,多項式編碼方案的最終完成時間與未編碼方案相比顯著增加.針對稀疏矩陣乘法問題,Wang等人[23]提出了一種“稀疏編碼”方案,其在編碼過程中充分利用了稀疏矩陣的特性,其恢復閾值可以以較高的概率達到mn,并且可以降低工作節點計算量.實驗結果表明,與未編碼方案、MDS碼[2]、乘積碼[19]、多項式編碼[20]和LT碼[81]相比,在不同稀疏矩陣乘法中,稀疏編碼方案都具有較快的計算速度,且對真實數據集的影響更為明顯.
我們在表4中對編碼計算方案的恢復閾值進行了總結和對比.其中工作節點個數為N,輸入矩陣A,B分別被劃分為p×m和p×n個子矩陣塊.

Table 4 Summary of Recovery Threshold in Coded Computing Schemes for Matrix-matrix Multiplication表4 矩陣-矩陣乘法編碼計算方案恢復閾值總結
3.2 面向機器學習典型運算的編碼計算
3.2.1 梯度下降算法編碼方案
Tandon等人[24]首次提出了梯度編碼(gradient coding, GC)這一概念,通過有效利用工作節點額外的計算和存儲,使得主節點能夠容忍部分隨機掉隊節點.基于GC思想有一系列研究方案[24-28],這些方案的共同特征是對梯度進行編碼.具體來說,對于一個由n個工作節點組成的分布式系統,GC的核心思想是首先將訓練數據集劃分n個不同的批次,隨后將r(1≤r≤n)個數據批分配給每個工作節點,接下來工作節點根據分配的數據集計算出r個部分梯度,并返回r個梯度的線性組合.這些線性組合使得主節點可以從任意n-r+1個工作節點的結果中恢復出全梯度(即,所有部分梯度的和).換句話說,基于GC的編碼方案的恢復閾值為K=n-r+1.
基于這種思想Tandon等人在文獻[24]中構造了2種梯度編碼方案:1)部分重復編碼(fractional repetition coding, FRC);2)循環重復編碼(cyclic repetition coding, CRC).分別對2種方案作簡要介紹.
1) FRC.假設系統中有s個掉隊節點,該方案首先將n個工作節點平均分為(s+1)個組,則每組有(n/s+1)個工作節點.隨后將訓練數據均等劃分為n個數據批,并分配給每個工作節點r=(s+1)個不相交的數據批,所有小組彼此互為副本.完成計算后,每個工作節點將其部分梯度的總和傳輸給工作節點.然而,這種構造只在n為s+1的倍數時適用.
2) CRC.與FRC構造不同,CRC編碼方案不需要n被(s+1)整除.在CRC中,不是分配不相交的數據批,而是考慮將(s+1)個數據批循環分配給工作節點.如圖8所示,為n=3,s=1的數據分配示例.假設每個數據批對應的梯度向量分別為g1,g2,g3,各個工作節點分別發送梯度的線性組合,例如g1/2+g2,g2-g3,g1/2+g3.主節點可以從任意2個向量中恢復g1+g2+g3:
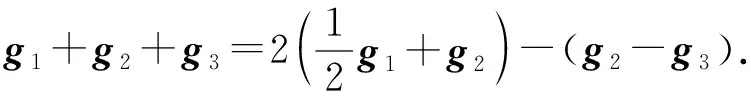
(11)
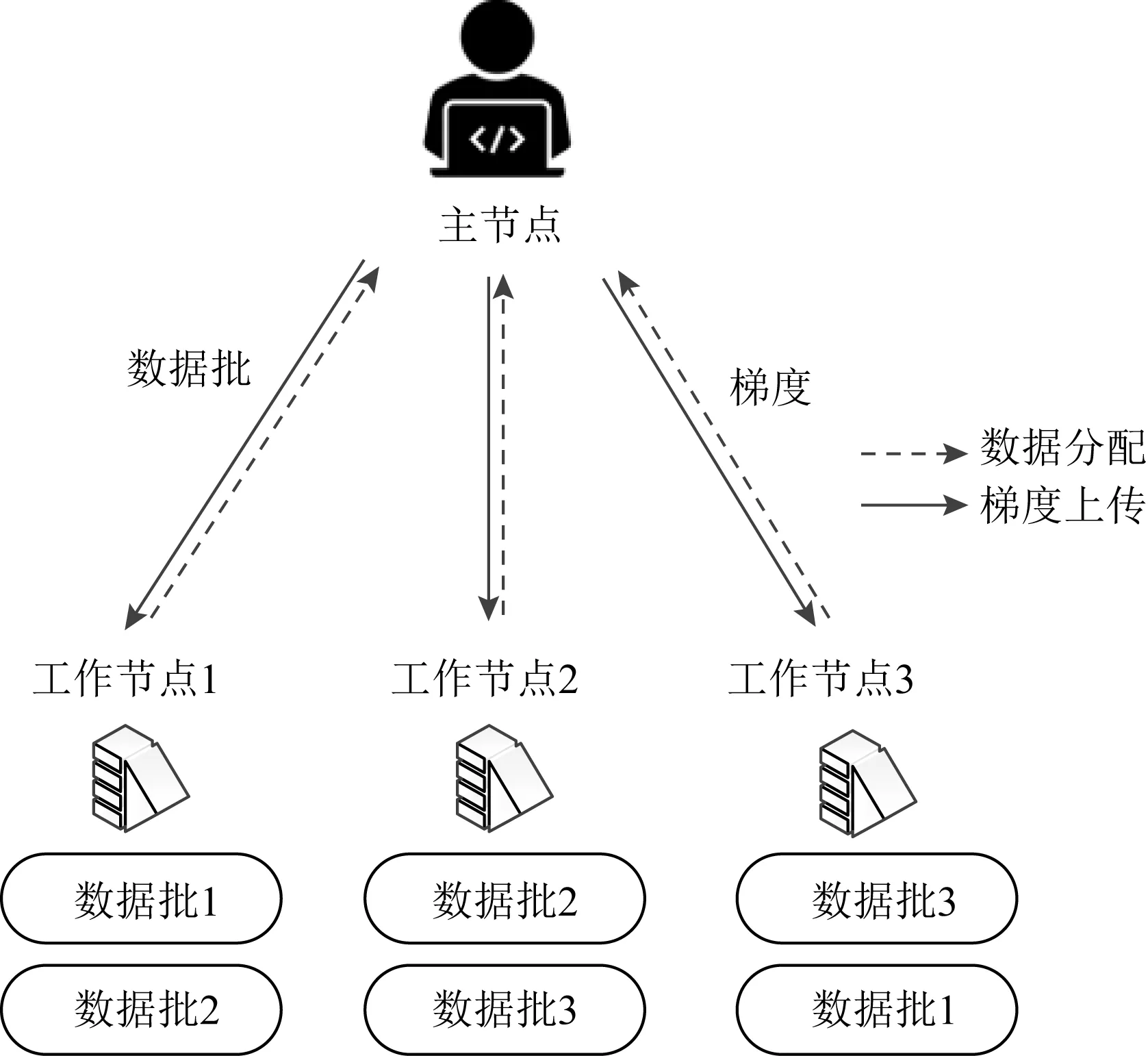
Fig. 8 Example of CRC when n=3,s=1圖8 n=3,s=1 CRC編碼示例
特別地,文獻[24]通過構造一個隨機編碼矩陣,從而指定數據分配以及局部梯度的線性組合的系數.以圖8為例,構造的編碼矩陣B應為

B中每一行的非零項的索引決定了分配給每個工作節點的數據批次,而每一行的值是每個工作節點對梯度進行線性組合編碼時的系數.在此基礎上文獻[26-27]分別使用循環(n,n-s)MDS碼[82]和Reed-Solomon碼[83]構造了相同功能的編碼矩陣,并達到了相同的性能,兩者的恢復閾值都為K=n-r+1.
3) BCC編碼方案.BCC方案[27]的核心思想是在主節點處獲得部分梯度的“覆蓋率”.簡單來說,將訓練樣本分成若干批,每個工作節點獨立地隨機選擇其中一個數據批進行梯度計算,隨后工作節點將計算的部分梯度的和返回給主節點.如果主節點之前已經接收到同一數據批的梯度,那么主節點將丟棄該消息,否則保留該消息.在接收到所有數據批的處理結果之前,主節點一直收集消息.最后,主節點通過簡單地計算保留的消息的總和恢復出最終結果.

4) 通信-恢復閾值平衡方案.除了恢復閾值外,通信成本也是影響分布式梯度下降算法的重要因素之一.然而上述文獻的重點在于實現最佳恢復閾值,并沒有考慮通信成本的問題.Ye等人[28]通過將梯度記為一個l維矢量,并對其中的元素進行線性編碼,從而用更大的恢復閾值來換取每個工作節點更少的通信量.
雖然文獻[28]同時權衡了恢復閾值和通信開銷,但該方案存在解碼復雜度高和數值穩定性差的問題.為了恢復梯度和,主節點需要計算一個大小為n-s(n為總節點數,s為掉隊節點數)的矩陣的逆矩陣,這導致文獻[28]的解碼復雜度為O(n3).Kadhe等人[84]針對該問題,設計一個允許使用任意線性代碼來實現編解碼功能的系統框架.該框架使用FRC[24]方案在工作節點之間分配訓練數據.當在這個框架中使用特定的碼時,它的塊長度決定了計算負載、維度決定了通信開銷、最小距離決定了恢復閾值.文獻[84]作者使用MSD碼在Amazon EC2上評估了該框架的性能,與文獻[28]相比,其平均迭代時間減少了16%.

6) AGC.與針對固定數目的掉隊節點方案不同,Cao等人[87]提出了一種具有靈活容忍度的自適應梯度編碼(adaptive gradient coding, AGC)方案.通過讓工作節點按輪次向主節點發送信號,該方案在計算負載,通信開銷和恢復閾值之間實現了最佳折中.在AGC中,假如系統中沒有掉隊節點,則主節點在接收到所有工作節點在第一輪返回的編碼梯度后即可解碼獲得總梯度;假如系統中有掉隊節點,則正常工作節點需要繼續返回編碼梯度,直至主節點可以解碼總梯度.因此,該方案適用于掉隊節點數量未知并且隨著算法迭代而變化的實際應用.表5對編碼梯度下降方案進行了分類,并總結了各方案的恢復閾值.
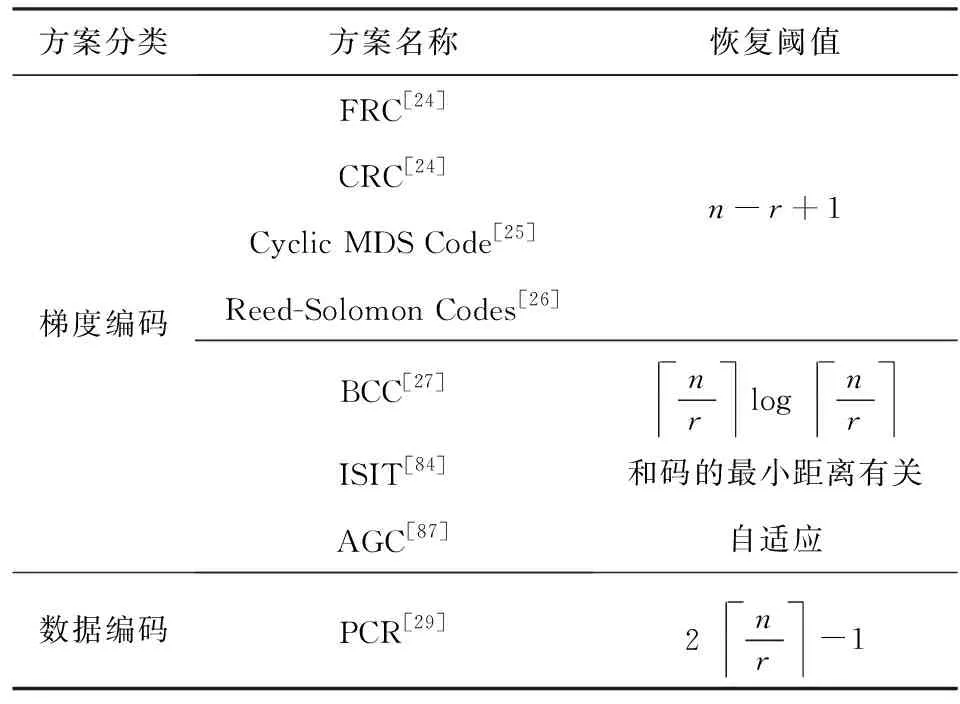
Table 5 Classification and Summary of Coded Computing Schemes for Gradient表5 編碼梯度下降方案分類和總結
3.2.2 卷積計算和傅里葉變換
1) 卷積計算.卷積運算在數學、物理、統計和信號處理中具有廣泛的應用.特別是對于卷積神經網絡來說,卷積常被用于過濾或提取特征.Dutta等人[30]針對受掉隊節點影響的分布式卷積計算系統,提出了一種新穎的編碼卷積策略.該編碼策略首先將輸入向量分割為長度一定的短向量,并使用MDS碼對預先指定的向量進行編碼,從而可以在目標時間內快速可靠地完成計算.
2) 離散傅里葉變換.離散傅里葉變換是包括信號處理,數據分析和機器學習算法等在內的許多應用程序的基礎操作之一.Yu等人[31]為了減少分布式離散傅里葉變換算法的計算延遲,提出了一種編碼傅里葉變換方案.該方案利用離散傅里葉變換的遞歸結構,首先將其分解為多個短向量上的離散傅里葉變換操作,其次利用傅里葉變換的線性特性,對輸入數據進行線性編碼,使工作節點的輸出具有一定的MDS碼特性,從而減少分布式計算的計算延遲.
3.2.3 非線性計算
由于神經網絡的某些層,如激活層是非線性的,所以算法的整體計算是非線性的.然而,本文討論的編碼計算方案并不適用于具有非線性計算的神經網絡.但這些網絡的性能也受到掉隊節點的限制.Dutra等人[88]提出的一種用于矩陣-向量乘法的Generalized PolyDot編碼方案,是可以擴展到深度神經網絡(deep neural network, DNN)的方法之一.Generalized PolyDot通過對DNN中每一層的線性運算進行編碼,從而允許每一層的訓練中出現錯誤.換句話說,在錯誤量不超過最大錯誤容忍度的情況下,解碼仍然可以正確執行.Hadidi等人[89]指出編碼技術可以有效降低IoT系統中不同神經網絡架構如AlexNet[90]中的計算延遲.但是,這種統一編碼DNN的策略可能不適用于其他具有大量非線性函數的神經網絡.現有的編碼計算方法側重于手工設計新的編碼方法,大多都不適合預測服務系統.
因此,Kosaian等人[32]在CNN和多層感知器的基礎上,提出了一種用來學習編碼和解碼功能的神經網絡結構和訓練方法.在沒有掉隊節點的情況下,解碼函數返回的預測結果與其他預測服務系統的結果相同.當出現掉隊節點時,解碼函數的輸出是對緩慢或失敗預測的近似重建.通過使用ResNet-18分類器在數據集MNIST,Fashion-MNIST和CIFAR-10上進行實驗,結果顯示該方案重建不可用,輸出結果的正確率分別為95.71%,82.77%和60.74%.
3.3 其他面向計算延遲的編碼計算方案
就適用場景而言,第3.1~3.2節所介紹的編碼計算方案中工作節點皆是同構的,而分布式計算中另一個常見特性是工作節點的異構性.因此,研究如何減少異構分布式計算場景下的計算延遲也是非常必要的.
1) 異構場景下編碼計算方案.為了更好地處理異構分布式計算系統中的掉隊節點,必須考慮設計有效的負載分配策略,以最大程度地減少總體作業執行時間.在給定計算時間參數,即每個工作節點計算時間服從一個移位的指數分布時,異構編碼矩陣乘法(heterogeneous coded matrix multiplication, HCMM)算法[33]解決了最優負載分配問題.HCMM方案利用編碼技術和計算負載分配策略,最大程度地減少了平均計算時間.仿真結果表明,相比于未編碼方案,未編碼負載平衡方案和統一的負載分配編碼方案,HCMM分別將平均計算時間分別減少了71%,53%和39%.
雖然HCMM顯著降低了計算延遲,但其解碼復雜度很高.在實際的分布式計算系統中,某些處理節點具有相同的計算能力分布,因此可以將它們組合在一起,形成一個群.通過利用這種群結構和不同群之間的異構性[34-35],并結合最優負載分配策略,不僅可以實現接近基于MDS碼的編碼方案的最佳計算時間,而且可以降低解碼復雜度.
除了工作節點的異構能力之外,工作節點的可用資源也可能隨時間而變化.為了最大化工作節點的資源利用率,研究人員提出了適應工作節點時變特性的動態負載分配算法[36-38].Keshtkarjahromi等人[36]提出了一種編碼協同計算協議(coded cooperative computation protocol, C3P).在C3P中,主節點基于工作節點的響應來確定編碼數據包的傳輸間隔.對于不能在給定的傳輸間隔內完成任務的工作節點,它們等待下一個編碼數據包的時間更長.與不考慮工作節點動態資源異構性的HCMM[33]相比,C3P協議的計算延遲降低了30%.
為了避免網絡中掉隊節點造成的延遲,大多數編碼計算方案都將掉隊節點視為“糾刪節點”,這意味著它們的計算結果將被完全忽略.然而很少有工作節點是完全不活動的,因此,掉隊節點,特別是非持久性掉隊節點所完成的計算結果是不可忽略的,需要更好地利用[91].
2) 利用掉隊節點的編碼計算方案.為了利用這些掉隊節點的計算能力,Ozfatura等人[39]使用了多信息通信(multi-message communication, MMC),其允許工作節點在完成分配任務的一部分時傳輸其計算結果.Ozfatura等人將MMC和拉格朗日編碼計算方案[48]相結合,以最大程度地縮短作業執行時間,但由于工作節點傳輸到主節點的消息數量增加而導致通信負載增加.Kiani等人[40]將分配給工作節點的任務進一步分為較小的部分,并且允許工作節點之間交流其各自計算結果,這使得掉隊節點所做的工作可以被充分利用.
Ferdinand等人[41]提出一種分層編碼計算方案,以利用所有工作節點的計算結果.在該方案中,每個工作節點將分配的計算任務按層劃分為多個子計算,然后按順序進行處理,即在下一層計算開始之前,需要將已完成層的子計算的結果傳輸到主節點.Ferdinand等人使用MDS碼對每層任務進行編碼,以使工作節點完成每層任務的計算時間大致相同.隨后該分層編碼計算方案被Kiani等人[42]擴展到分布式矩陣-矩陣乘法和矩陣-向量乘法中.對于這2種類型的乘法,Kiani等人通過實驗表明,雖然解碼時間有所減少,但是分層編碼的計算時間要比文獻[39]中的方案長.
雖然編碼計算方案可以降低通信負載并減少作業執行時間,但未編碼的計算方案具有其自身的優勢,即不需解碼并允許部分梯度更新.為了結合2種方案的優點,Ozfatura等人[43]提出了編碼部分梯度計算(coded partial gradient computation, CPGC)方案.因為每個工作節點都有很高的概率完成第一次分配的任務,所以CPGC首先分配給工作節點未編碼的子矩陣,在工作節點完成計算后,再分配給其編碼子矩陣.主節點能夠使用一部分工作節點的全部計算結果和掉隊節點的部分計算結果來更新梯度參數,從而減少任務執行的平均時間.
3.4 小 結
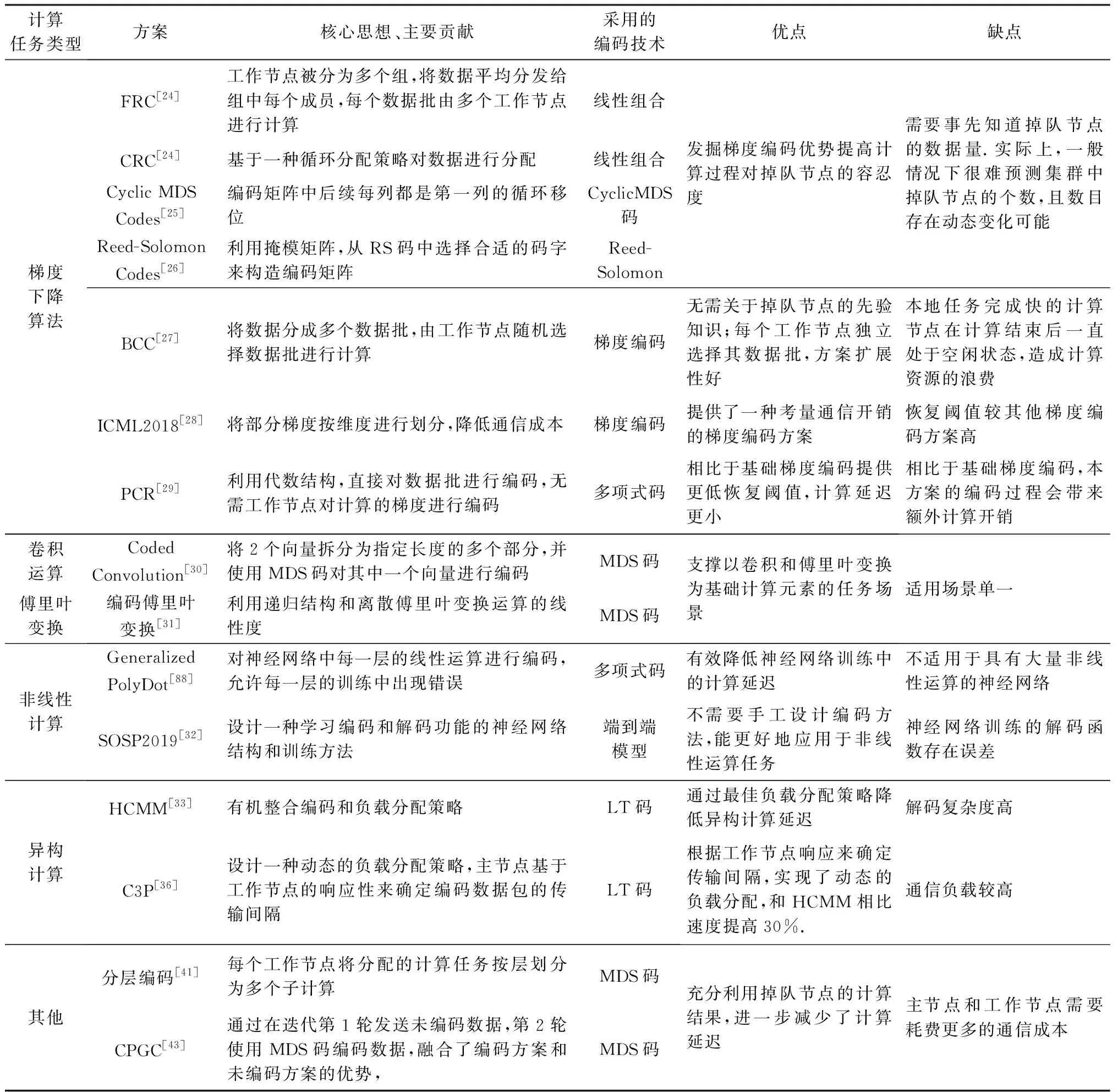
本節我們探討編碼技術在不同分布式計算任務中的應用.首先對3.3節方案進行總結回顧,如表6所示:
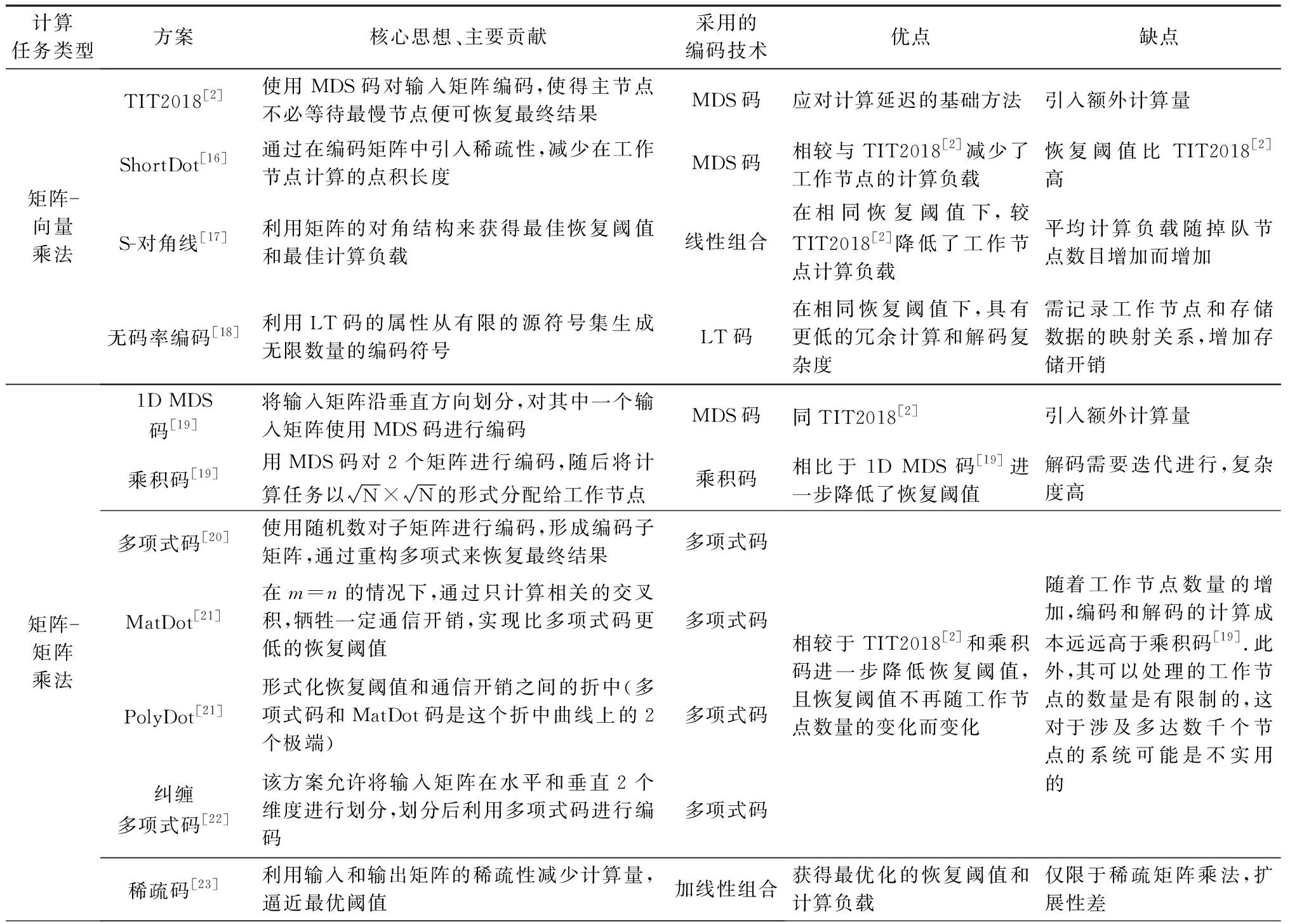
Table 6 Summary and Review of Coded Computing Schemes for Computing Delay表6 面向計算延遲的編碼計算方案總結與回顧
續表6
在矩陣-向量乘法任務中,研究人員不僅考慮如何使得恢復閾值最小,而且考慮了如何降低工作節點處的計算負載,以從整體上降低計算時間.特別地,無碼率編碼[18]可以有效利用掉隊節點所做的工作,但該方案工作節點和主節點通信輪次增高,帶來較大的通信開銷.在矩陣-矩陣乘法中,現有研究方案都先將輸入矩陣劃分為較小的子矩陣,然后對子矩陣進行編碼,生成編碼矩陣.乘積碼[19]使用MDS碼在2個維度上對矩陣進行編碼,多項式碼[20]、MatDot[21]、PolyDot[21]、糾纏多項式碼[22]則使用隨機數對子矩陣進行編碼,只不過在矩陣分割形式上有所不同.文獻[20-22]解碼最終結果的方法都可看成多項式插值問題.但這些方案都未考慮矩陣的稀疏性,因此研究人員提出了稀疏碼方案[23],在計算速度上較其他方案有較大優勢.梯度下降編碼方案則大致可分為2類:1)基于GC的編碼方案[24-27],這些方案中工作節點返回局部梯度的線性組合;2)對數據進行編碼的方案,雖然該方案的恢復閾值比GC編碼方案低,但其對數據進行編碼帶來了額外的計算開銷.
雖然大多數的研究都集中在編碼的設計上,但是譯碼復雜度和工作節點的計算負載也會對計算時間產生很大的影響.因此面向計算延遲的編碼計算方案不應僅以降低恢復閾值為目標,而應權衡恢復閾值,計算負載和譯碼復雜度三者之間的關系,從而使整體計算時間最短.除了Reed-Solomon碼[81]和LDPC碼[85],更有效的低復雜度解碼方式需要進一步探索.
4 面向安全隱私的編碼計算
在分布式計算系統中,好奇的工作節點可能串通起來以獲取原始數據的信息,而受到拜占庭攻擊的惡意工作節點可能故意提供錯誤的結果[92],從而誤導最終結果.抗惡意節點的編碼計算方案往往通過設計具有糾錯能力的解碼方式以定位惡意節點,從而獲取正確結果.防隱私泄露的編碼計算方案則通過引入一個隨機均勻矩陣對輸入數據進行編碼,從而達到掩藏真實數據的目的.
面向安全隱私的編碼計算方案的目標是通過利用編碼技術,在系統中存在M個惡意節點和T個共謀節點時,依然可以獲得正確結果,并且不泄露原始數據的任何信息.我們將分別從抗惡意節點和防隱私泄露2方面對當前編碼計算方案進行分析.
4.1 抗惡意節點的編碼計算
在分布式計算的應用場景中,如戰場物聯網[93]、聯邦學習[94]等,工作節點的計算可能是不可信的.因此,一個重要的問題是是否能夠在拜占庭敵手的存在下可靠地執行分布式計算,并且該問題由來已久[95].最近,編碼技術被應用到分布式計算系統中,以抵抗分布式計算系統中的拜占庭攻擊問題.
1) DRACO.在分布式梯度下降算法中,Chen等人分別利用FRC和CRC[24]對數據進行編碼(具體編碼方法見4.3節),并針對2種不同的編碼方法,設計了2種不同的解碼方案.
具體來說,利用FRC對數據進行編碼時,DRACO[44]讓每一組中的節點來計算相同的梯度的和.為了解碼同一組中的計算節點返回的輸出,主節點使用多數投票算法來選擇其中一個值.這保證了只要每組中少于一半的節點是惡意的,主節點將選擇到正確的結果.由此,主節點可以獲得所有組的正確的結果.利用CRC對數據進行編碼時,DRACO利用離散傅里葉逆變換矩陣構造一個函數φ(·).函數φ(·)可以利用文件分配矩陣來計算惡意工作節點的索引.因此,DRACO可以利用非惡意節點返回的值來解碼最終結果.仿真結果表明,DRACO算法在MNIST數據集上實現90%的測試精度時,比中值聚合方案[96]快3倍以上.隨后,Rajput等人[97]使用梯度濾波器進一步提高了DRACO的計算效率.
2) 響應冗余.Gupta等人[45]提出“響應冗余”的概念,并利用隨機檢測的方法來提高系統的工作效率.其核心思想是讓工作節點響應2次,且在每次響應中,為同一個工作節點分配不同的子數據集.通過對比2次響應的結果,主節點可以確定系統中惡意節點的索引.
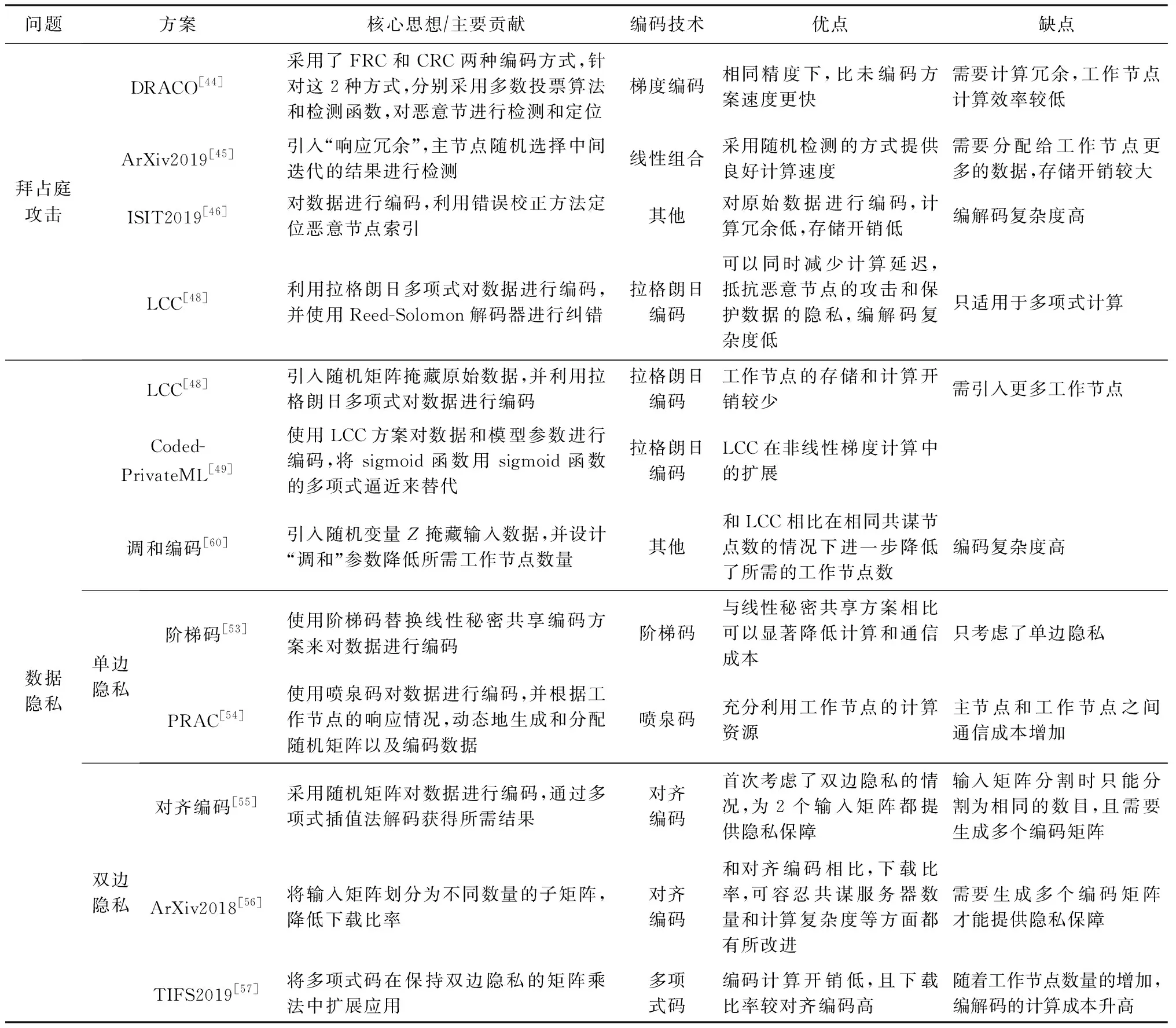
然而,引入響應冗余使得工作節點的計算成本比DRACO[44]高2倍.為了降低計算成本,Gupta等人提出了隨機方案,即主節點隨機選擇中間迭代的結果進行檢測,或者,在每一次迭代中,主節點以概率p(0 4) LCC.針對任意多元多項式的計算任務,Yu等人[48]提出一種拉格朗日編碼計算方案,該方案對輸入數據進行編碼,不僅可以降低計算延遲,而且可以抵抗惡意節點的攻擊,同時保護數據的隱私. 考慮一個具有N個工作節點的分布式計算系統,其目標是對大型數據集X=(X1,X2,…,XK)中每一個Xi,計算f(Xi)(f是給定的階為deg(f)的多元多項式).如果通過利用合適的編碼方法可以在系統中存在S個掉隊節點,A個惡意節點,T個合謀節點時仍然獲得正確結果且不暴露數據隱私,則認為該方案可以實現三元組(S,A,T). 如果N≥(K+T-1)deg(f)+S+2A+1,則LCC可以實現三元組(S,A,T).該結果的意義在于,增加一個工作節點(即N增加1),LCC可以使掉隊節點的彈性增加1,或者使惡意節點的魯棒性提高1/2,同時保持數據的隱私. (12) LCC可以應用于計算任務是多元多項式的任何計算場景,因此涵蓋了機器學習中許多計算任務,例如,線性計算、雙線性計算、一般張量代數和梯度下降. 在分布式計算模型中,要計算的輸入數據可能包含大量敏感信息,如個人位置信息和醫療信息.但是主節點有時需要利用可疑但有用的工作節點.因此保護輸入數據的敏感信息不被泄露變得至關重要. 4.2.1 面向多項式運算的隱私編碼方案 作為LCC的擴展,So等人[49]提出了一種快速且具有隱私保護功能的分布式機器學習框架——CodedPrivateML.該框架在每一輪訓練中分2步秘密共享數據集和模型參數.首先,采用隨機量化方法將數據集和每輪的權重向量轉換為有限域.然后,CodedPrivateML使用LCC編碼技術將量化值進行編碼,并將編碼數據分發給各工作節點,以保證數據隱私.CodedPrivateML面臨的挑戰是:LCC只能用于多項式求值形式的計算.因此,CodedPrivateML利用多項式逼近來處理涉及到sigmoid函數時的非線性計算,從而可以對LCC編碼的數據進行Logistic回歸.在Amazon EC2集群上的實驗表明:CodedPrivateML比基于BGW[51]的安全多方計算方法快34倍,并且可以保護數據的隱私. 針對梯度類型的計算,Yu等人[60]提出了一種新穎的編碼計算方案,稱為“調和編碼”,該方案適用于任何類型的梯度計算,同時可以保護輸入數據的隱私.和LCC不同的是,調和編碼使用一個隨機變量Z來構造具有遞歸結構的中間值P,然后使用P對數據進行編碼.由于Z是隨機的,因此原始數據被掩藏,數據隱私得到保護.又由于中間值P的特殊結構,所以使得該方案相比于Shamir秘密共享方案[98]和LCC[48]方案,在計算梯度型函數時需要更少的工作節點.表7總結了3種方案在保護數據隱私時所需的最少工作節點數. Table 7 Comparison of the Minimum Number of Working Nodes表7 最少工作節點數對比 利用多項式碼[20]可以有效降低分布式計算系統中的計算延遲,且恢復閾值與工作節點的數量無關.在此基礎上,Nodehi等人[50]將多項式碼與BGW方案[51]結合在一起,提出了一種多項式共享方案.在該方案中,數據源自外部資源,因此必須對工作節點和主節點同時保持私有.與BGW方案不同,Nodehi等人使用多項式碼對數據集進行編碼.文獻[50]可用于執行加法、乘法和多項式函數等多種計算過程,同時可以減少完成任務所需的工作節點數. 在文獻[50]中,執行計算的數據集被分成多個子數據集,每個子數據集被編碼并分配給工作節點.在這種情況下,較快完成任務的工作節點將在等待掉隊節點時處于空閑狀態.為了進一步減少計算延遲,Kim等人[99]利用計算冗余提出了一種私有異步多項式編碼方案,該方案將一個計算任務分成幾個相對較小的子任務,并將子任務分配給每個工作節點.除了保留多項式共享方案的隱私保護特性外,該方案有2個優點:1)計算能力有限的掉隊節點可以成功地完成較小的子任務;2)計算速度較快的工作節點被分配更多的任務,在整個任務計算期間持續工作,從而減少了整個任務的執行時間. 然而,文獻[50,99]主要利用多項式碼來保護數據隱私,這在某些方面是有限制的,例如,它只允許將矩陣按列劃分.因此,Nodehi等人[100]利用糾纏多項式碼[22]提出了一種糾纏多項式碼共享方案,該方案作為多項式共享的擴展,進一步減少了數據共享階段的限制,從而在滿足隱私約束的同時減少執行相同計算任務所需的工作節點的數量. 4.2.2 面向矩陣乘法運算的隱私編碼方案 針對矩陣乘法的特點研究人員考慮了2種隱私情況: 1) 單邊隱私.輸入數據中只有一個是私有的,另一個輸入對工作節點是公開的. 2) 雙邊隱私.2個輸入數據都是私有的,工作節點無法獲得所有輸入的有關信息. 分別對2種隱私情況下的編碼計算方案進行介紹和分析. 單邊隱私.Bitar等人[52-53]提出使用階梯碼替換線性秘密共享方案[101]來對數據進行編碼.作為說明,考慮一個有3個工作節點的分布式計算場景,其目標是分布式計算矩陣-向量乘法Ax,并保護輸入數據A的隱私(單邊隱私).為保護數據隱私,主節點生成一個與A具有相同維數的隨機矩陣R.當使用線性秘密共享方案時,數據和隨機矩陣不被分割,作為一個整體進行編碼和傳輸,如表8所示: Table 8 Transmission Contents of Two Different Schemes表8 2種不同共享方案的傳輸內容 因此,主節點必須等待其中任意2個工作節點的完整結果,才能解碼最終結果,如Ax=S2x-S1x.當使用階梯碼時,數據和隨機矩陣在傳輸給工作節點之前被分割成子矩陣.隨后主節點發送給工作節點2組編碼數據,如表8所示.因此,每個工作節點有2個子任務.每個工作節點按順序執行計算任務,并將計算結果返回給主節點.當工作節點完成了足夠多的子任務后,主節點可以通知工作節點停止計算.例如,當主節點接收到所有工作節點的第一個子任務的計算結果,或者主節點接收到任意2個工作節點的所有任務的結果時,可以從中解碼獲得最終的結果.在有4個工作節點的分布式計算場景下,Bitar等人在Amazon EC2集群上進行實驗,結果表明使用階梯碼的平均等待時間比線性秘密共享方案減少了59%. Bitar等人[54]考慮到戰場物聯網(internet of battlefield things, IoBT)應用和設備的隱私要求,以及戰場邊緣設備資源的異構和時變性,提出了一種私密無速率自適應(private and rateless adaptive coded computation, PRAC)編碼計算方案.和階梯碼相同,PRAC也引入隨機矩陣來掩藏原始數據,但不同的是PRAC考慮了工作節點的異構性,使用噴泉碼[81]對數據進行編碼,并根據工作節點的響應情況,動態地生成和分配隨機矩陣和編碼數據. 雙邊隱私.Chang等人[55]首次考慮了矩陣乘法中雙邊隱私的情況,并設計了一個可行性方案.具體來說,輸入矩陣被分割成子矩陣并用隨機矩陣編碼.以工作節點數為8、共謀節點數為1,來說明文獻[55]的編碼過程. 主節點首先將輸入矩陣A,B進行劃分 (13) 其中,A1,A2∈m/2×n,B1,B2∈n×p/2.然后,分別為A,B各生成一個隨機矩陣KA∈m/2×n,KB∈n×p/2.主節點為每個工作節點i選擇不同的參數xi,生成編碼數據為 (14) (15) h(x)=A1B1+A2B1x+KAB1x2+A1B2x3+A2B2x4+(KAB2+A1KB)x5+A2KBx6+KAKBx7. (16) 由式(16)可知,多項式h(x)中4項A1B1,A2B1x,A1B2x,A2B2x的系數可組成最終結果.因此,主節點可以采取多項式插值法確定該多項式,從而獲得所需的系數. 在該編碼思想的基礎上,Kakar等人[56]針對雙邊隱私提出了一種新的任意矩陣劃分下的對齊秘密共享方案,以優化下載比率和恢復閾值.與文獻[55]將2個輸入矩陣劃分為相同數量的子矩陣不同,Kakar等人[56]將輸入矩陣劃分為不同數量的子矩陣.與文獻[55]相比,文獻[56]在下載比率、可容忍共謀服務器數量和計算復雜度等方面都有所改進. 受多項式碼[20]的啟發,Yang等人[57]將多項式碼擴展到保護雙邊隱私的矩陣乘法中.和文獻[55-56]不同,該方案僅需為每個輸入矩陣生成1個隨機矩陣便可完成編碼.主節點的解碼過程與多項式碼方案相似,都可視為多項式插值問題.和文獻[56]相比,該方案的編碼復雜度要低,并且在下載比率相似的情況下,可實現更低的恢復閾值. 本節我們討論了編碼計算在分布式計算系統中對抗惡意節點以及保護數據隱私方面的應用和研究.首先我們對4.1~4.2節方案進行總結和回顧,如表9所示. 抗惡意節點的編碼計算方案往往通過設計具有糾錯能力的解碼方式以獲取正確結果.DRACO[44]采用文獻[24]中FRC和CRC兩種編碼方式,但在解碼階段分別引入了多數投票算法和檢測函數.Gupta等人[45]采用基于GC的編碼方式對梯度進行編碼,但解碼階段則引入響應冗余,用以檢測惡意節點.Data等人[46]在編碼階段設計具有錯誤校正能力的編碼矩陣,利用該矩陣對輸入數據進行編碼,以在解碼階段可以對惡意節點進行定位.LCC[48]通過構造多項式的方式對數據進行編碼,并在解碼階段利用具有糾錯能力的Reed-Solomon解碼器進行解碼.防隱私泄露的編碼計算方案在對數據進行編碼時,額外引入一個隨機矩陣,以此對原數據進行掩藏.特別是,針對矩陣乘法任務,本節討論了單、雙邊隱私2種情況.一般來說,利用特定運算的代數結構,例如卷積任務或梯度計算,實現編碼和解碼的方案通常表現更高效. Table 9 Summary and Review of Coded Computing Schemes for Security and Privacy表9 面向安全和隱私的編碼計算方案總結和回顧 目前,關于編碼計算在學術界的研究才剛剛起步,存在許多問題需要解決,提供一系列研究機遇,本文從3個方面對未來可能的研究方向進行闡述. 1) 通信與計算的松耦合.在將編碼應用于數據洗牌的相關工作中,通信和計算是松耦合的.即,其只關心通信目標:主節點希望以最小的通信負載使得每個工作節點都能獲得執行計算任務所需要的數據.為了實現最小化通信負載,往往需要計算節點額外存儲大量數據(存儲冗余),而這些冗余數據只幫助傳輸并不用于計算[15]. 未來一個可能的工作方向是提高通信與計算的耦合性.如果多余的存儲數據用于計算,則可以獲得潛在的計算增益.例如,在訓練一個分類器模型時,多余的數據樣本也有助于模型訓練.設計一個計算和通信耦合度較高的方案,并研究其中通信與計算兩者之間的折中是必要的. 2) 掉隊節點的利用和通信負載的平衡.雖然掉隊節點的運行速度比平均速度慢,但其完成的計算結果對仍然有助于實現最終計算任務.例如,在文獻[58]中,為了使線性逆求解器在截止期約束下的均方誤差最小,掉隊節點的結果被視為軟誤差.然而,當前利用掉隊節點計算結果的方案中,往往需要執行更多的通信輪次.而高通信成本是分布式計算系統的另一個瓶頸.未來一個可能的研究方向是在利用掉隊節點的計算結果時,探索使主節點和工作節點之間通信成本最小化的優化方法. 3) 安全隱私中的異構.由于掉隊節點是分布式計算中的一個基本問題,因此面向計算延遲的編碼計算方案考慮了異構場景.然而,在編碼計算相關工作中,其他方面的異構網絡問題還沒有得到充分的研究[57].例如,工作節點可能有不同程度的聲譽[102].保護數據隱私的手段可以只針對新工作節點或聲譽低的工作節點進行,而對于受信任的工作節點則可能不需要.因此,未來一個可能的研究方向是考慮工作節點在聲譽上的異構性,從而采取不同的隱私保護策略,以此降低可信節點的計算復雜度. 幾十年來,編碼理論在抗噪聲方面的作用得以深入研究,并被廣泛應用于多種場景中,成為日常基礎設施(如智能手機、筆記本電腦、WiFi和蜂窩系統等)的一部分.編碼計算將編碼理論和分布式計算系統相結合,旨在通過注入計算冗余創造編碼機會,實現降低通信成本、提高計算速度和保護數據安全等目標.本文通過區分研究目標將已有編碼計算方案分為3類,對相應范疇下的研究現狀進行了詳細闡述,對比分析了典型方案,總結歸納了編碼計算面臨的挑戰及研究方向,預期為分布式計算的研究人員帶來啟發和參考. 作者貢獻聲明:蔡志平是本項目的構思者及負責人,指導論文寫作;周桐慶對本文關鍵性理論和知識性內容進行批評性審閱;鄭騰飛是綜述的主要撰寫人;吳虹佳完成相關資料的收集和分析.周桐慶和蔡志平貢獻等同,同為本文通信作者.
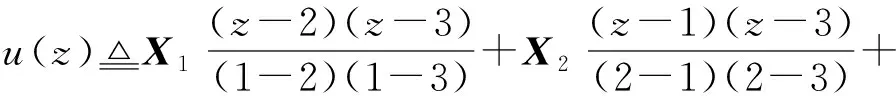
4.2 防隱私泄露的編碼計算


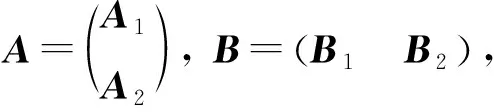

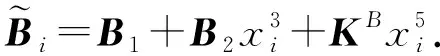
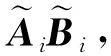
4.3 小 結
6 研究展望
7 結束語

