基于優化后灰色模型的庫瑪拉克河年徑流量預測分析

劉新華，劉 斌，張桂林

（1.新疆塔里木河流域阿克蘇管理局，新疆 阿克蘇 843300；2.新疆農業大學水利與土木工程學院，烏魯木齊 830052）

水資源是人類生存和發展不可缺少的自然資源，是維系干旱內陸河生態安全的關鍵要素。HADDELAND等[1]通過氣候變化情景分析預測水循環變化，進而發現水資源在時間和空間上分配十分不均，研究徑流量的變化特征與規律對流域水資源綜合管理至關重要。徑流量受自然因素和人為因素的影響，它的變化規律既有確定性，也有隨機性[2]。

河川徑流量的預測方法有很多，常用的有小波分析、遺傳算法、BP神經網絡、GM(1,1)等。各種方法均有優劣，要根據氣候、環境、樣本數據等情況選擇適當的預測方法。本文采用優化的灰色模型對阿克蘇河的主要支流庫瑪拉克河年徑流量進行預測。早在1982年，灰色系統理論由學者鄧聚龍在國際上第一次提出[3]。1992年，劉毅等[4]以灰色預測為基礎，提出灰色拓撲模型，并將其應用在長江三峽水利工程科研工作中。歐建鋒[5]針對水利現代化影響因素的復雜、可用信息相對單一的特點，運用灰色模型對江蘇水利現代化進程進行預測，得到今后10年的江蘇水利現代化發展水平。2019年，李強等[6]利用灰色分析法對我國水資源發展現狀進行預測。傳統的GM(1,1)是一種不嚴謹的預測模型，它忽略了系統結構分析，預測結果出現一次增大或減小的現象。灰色拓撲模型解決了傳統GM(1,1)缺乏波動性的缺點，但其本身缺乏波峰、波谷的趨勢性預測。

本文通過提出優化的GM(1,1)，結合傳統GM(1,1)對徑流量波峰、波谷的趨勢預測和灰色拓撲模型對時間的周期性預測特點，對庫瑪拉克河2020-2029年徑流量進行預測。同時利用2017年、2018年、2019年的徑流量數據（53.6億m3、40.25億m3、40.88億m3）對優化后的GM(1,1)進行校核，得到更加可靠的預測結果，為阿克蘇地區水資源的管理和調控提供數據基礎。

1 優化的灰色預測模型

1.1 方法簡介

灰色模型是一種研究貧信息、小樣本和不確定性的方法[7]。但是，灰色預測模型是一種特定的指數曲線，它只能預測出徑流量的變化趨勢性，無法對徑流量的波動性進行預測。同時，原始數據的波動性對灰色模型的預測精度有一定影響[8]，在平均值上下浮動超過5%時，傳統的GM(1,1)得到的預測結果出現一次增加或減少，對波動起伏大且不規則變化的樣本來說，預測結果誤差較大[9]。

灰色拓撲模型又稱波型預測，是對一個變化不規律的樣本數據進行預測，反映系統的起伏波動狀況[10]。灰色拓撲模型的預測結果具有隨機性，但它的預測結果缺乏趨勢性，并且當選擇閾值對應的樣本數據太少時，預測結果出現缺漏，當閾值對應的樣本數據過多時，一年內會出現多個徑流量預測結果。

優化的GM(1,1)通過把傳統的GM(1,1)與灰色拓撲模型相結合，使其擁有趨勢性和波動性的預測特點，保證徑流量的預測結果更加接近實際變化情況。

1.2 GM(1,1)模型

灰色模型具有微分、差分、指數兼容的性質,即灰色模型通過建立差分方程，推導出微分方程，得到具有指數性質的時間響應函數對原始數據進行擬合和預測[11]。一階累加時，設變量為X(0)的原始數據序列為：

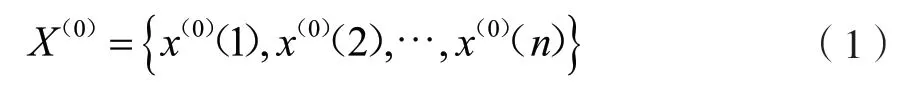
生成一階累加數列，即

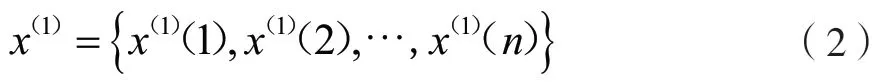
其中，x(1)(n)滿足以下條件：

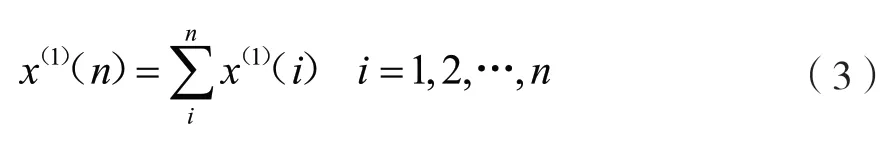
令矩陣Y和矩陣B滿足以下條件：

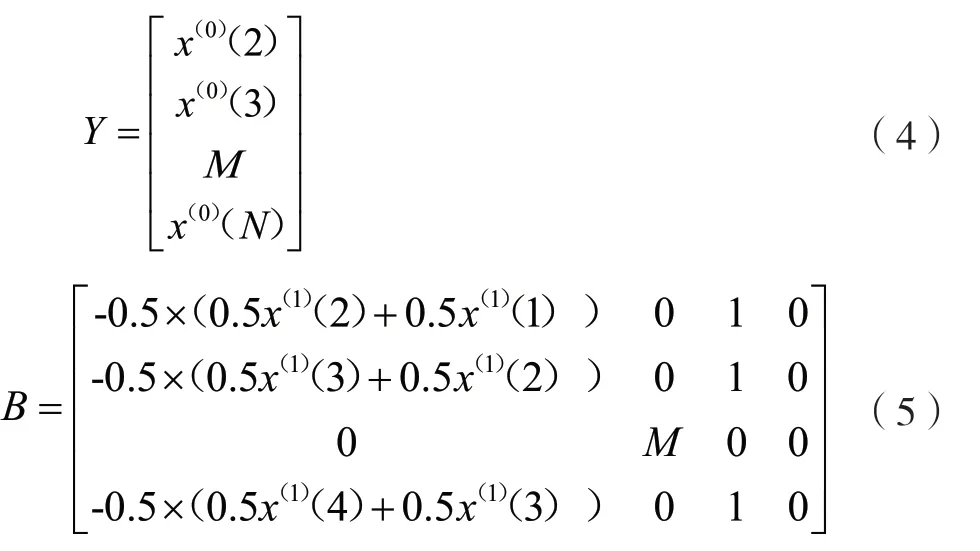
由式（4）和式（5）可得，a的最小二乘法估計a^為：

參數b滿足以下條件：

式（7）被稱為灰微分方程的白化方程，則白化微分方程的解（時間響應函數）為：

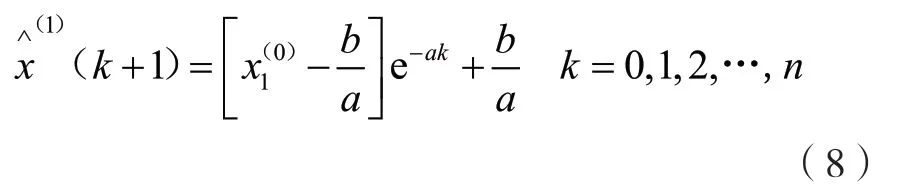
累減還原預測公式為：

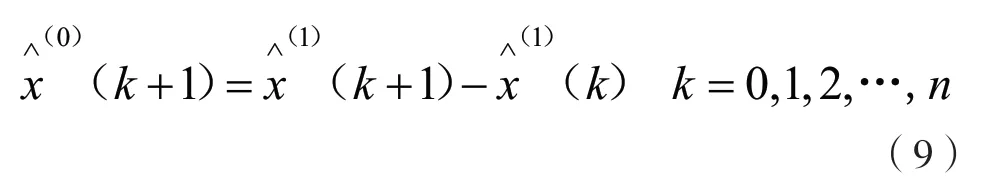
GM(1,1)的精度檢驗流程如下：求出GM(1,1)的原始序列方差、殘差序列方差后驗差比值C、小誤差概率P，根據表1確定模型精度級別。模型精度級別=Max{C所處級別，P所處級別}[12]。

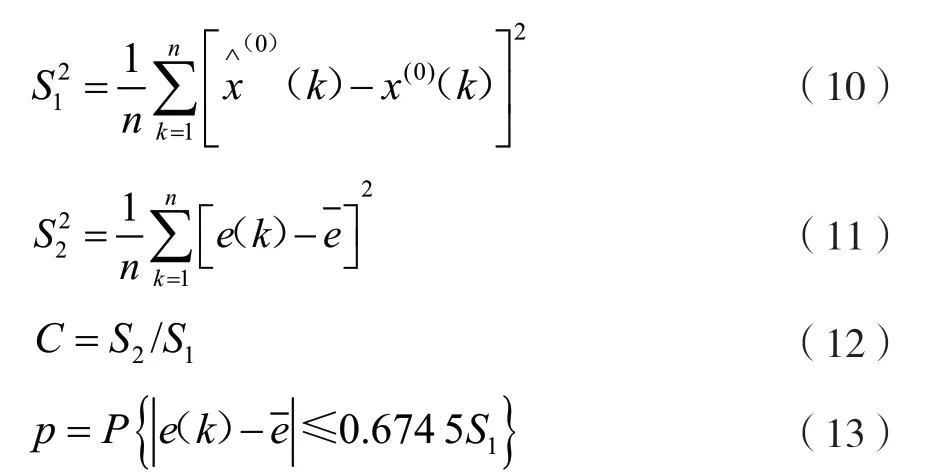
表1 模型精度等級

1.3 灰色拓撲模型

第一步，X(0)(k)為徑流量原始序列，根據點(k,X(0)(k))在平面上描繪出一條曲線，X(0)(k)中最大值記為maxX(0)，最小值記為minX(0)，平面上給定一系列均勻的閾值λi，i=1,2,…,m，則有minX(0)≤λi≤maxX(0)。對于每一個閾值λi，有映射λi:{X(0)}→{t(0)i}，其中，t(0)i(k)是水平線λi與曲線X(0)相交第k個點的橫坐標值；有映射Q:{t(0)i,λi}→{t(0)i(k)}，k=1,2,…,n，Q為橫坐標的投影算子，即t(0)i(k)={t(0)i(1),t(0)i(2),…,t(0)i(ni)}。對每一個t(0)i建立優化的GM(1,1)模型[13]。

第二步，求出后驗差比值C和小誤差概率C，通過表1查C和P的值確定預測模型的精度。

第三步，利用GM(1,1)對時間數據進行預測，把預測時間與對應的閾值描繪在平面上，得到灰色拓撲模型曲線。

1.4 優化的GM(1,1)

步驟一，確定一個隨時間變化的徑流量樣本數據。令X(0)滿足以下條件：

式中：x(0)(n)為第n年的徑流量。

步驟二，劃分范圍。若徑流量樣本中出現|X(0)-≥5%，則會導致灰色模型的預測結果出現指數上升或指數下降，這樣得到的預測結果不具有參考意義，但是實際情況下，在幾十年的徑流量樣本中基本都會出現|X(0)-X—|/X—≥5%這種狀況。所以，要以樣本平均值的10%進行范圍劃分，其分別為A1、B1、…、Z1。令三者滿足以下條件：

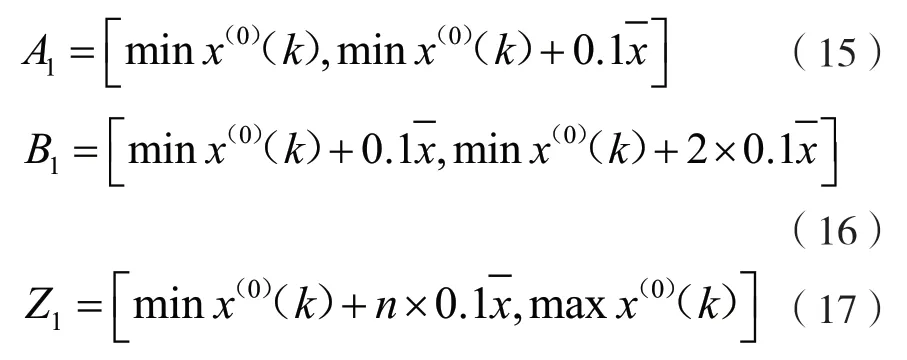
步驟三，確定樣本。尋找步驟二中得到的多個徑流量樣本和與之對應的時間樣本。

閥域A1的徑流量樣本與時間樣本分別為：

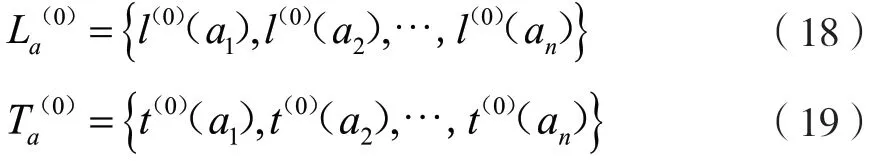
式中：La為徑流量樣本；Ta為時間樣本；l(0)(a1)為在閥域A1里面最小的實測徑流量數據，其他以此類推；t(0)(a1)為在閥域A1里面最小的實測徑流量對應的年份，其他以此類推。

閥域B1的徑流量樣本與時間樣本分別為：

式中：Lb為徑流量樣本；Tb為時間樣本；l(0)(b1)為在閥域B1里面最小的實測徑流量數據，其他以此類推；t(0)(b1)為在閥域B1里面最小的實測徑流量對應的年份，其他以此類推。

閥域Z1的徑流量樣本與時間樣本分別為：

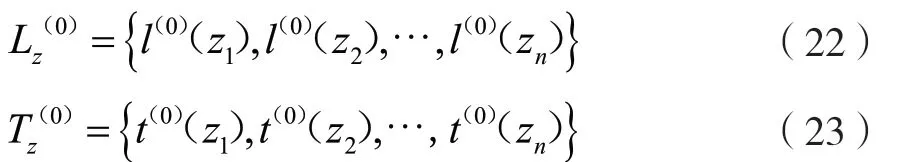
式中：Lz為徑流量樣本；Tz為時間樣本；l(0)(z1)為在閥域Z1里面最小的實測徑流量數據，其他以此類推；t(0)(z1)為在閥域Z1里面最小的實測徑流量對應的年份，其他以此類推。

步驟四，樣本疊加。對時間樣本中的原始數據進行疊加，從而削弱原始數據的隨機性，發現樣本的規律[14]。閥域Z1的疊加結果為：

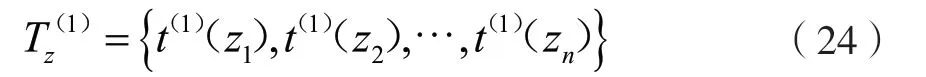
步驟五，參數Z(1)(zk)滿足以下條件：

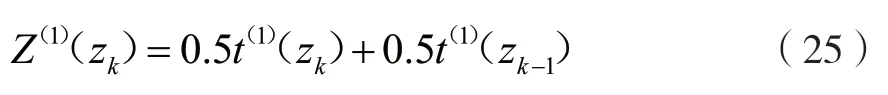
令矩陣Y和矩陣B滿足以下條件：

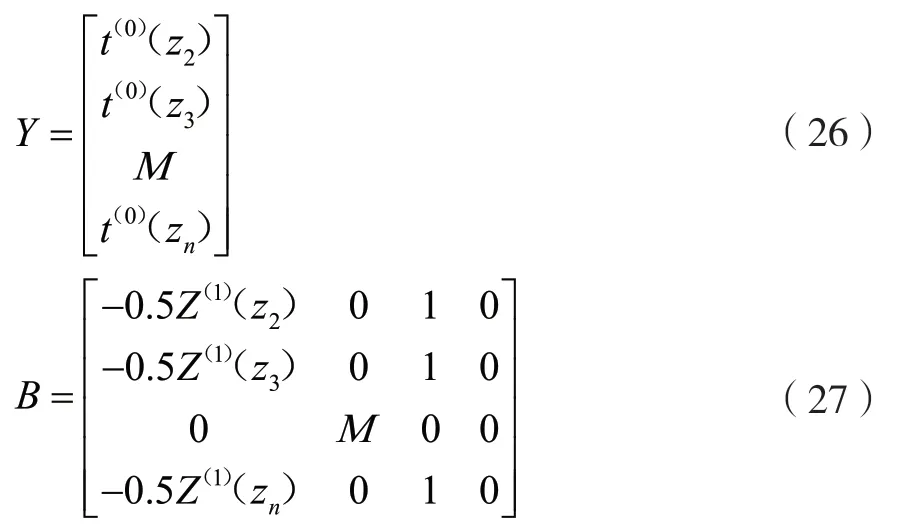
由式（26）和式（27）可得，a的最小二乘法估計為：

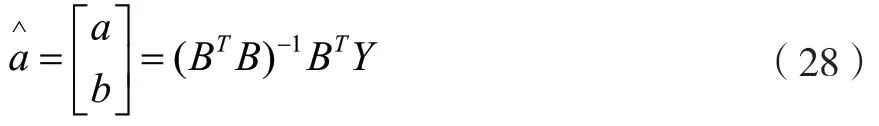
步驟六，把式（28）寫成離散形式：

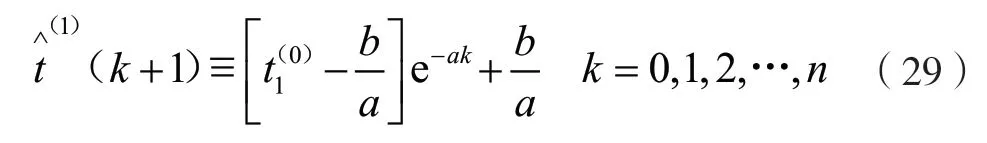
式（29）被稱為GM(1,1)的時間函數模型，再經過累減運算可得到原始數列t(0)的預測模型：

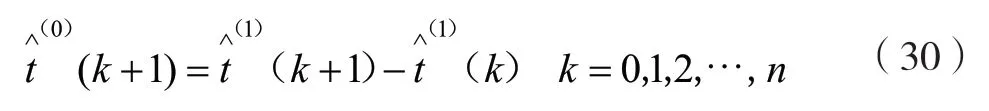
步驟七，精度檢驗。求后驗差比值C和小誤差概率P，根據表1得到模型精度。

步驟八，對徑流量樣本A1、B1、…、Z1建立GM(1,1)函數。重復第四步到第七步的過程，得到徑流量GM(1,1)函數。

步驟九，把不在樣本數據中的已知徑流量數據與通過模型得到的預測值做對比，分析模型精度。

步驟十，把時間模型和徑流量模型預測結果一一對應，得到徑流量預測結果。

2 模型應用

2.1 研究區概況

庫瑪拉克河位于新疆維吾爾自治區阿克蘇地區，處于亞歐大陸腹地，降雨量少、日照強、蒸發量大，屬于大陸性氣候。該河流發源于天山西段中部的汗騰格里峰西北坡，流域流經吉爾吉斯斯坦和哈薩克斯坦進入我國境內，主要水文斷面有協合拉渠首、土木秀克分水閘、多浪渠首。其中，協合拉引水樞紐位于庫瑪拉克河出山口，是庫瑪拉克河流入我國境內的水文站。根據協合拉水文站1958-2019年的監測數據，庫瑪拉克河的多年平均徑流為48.48億m3，其中1958-1977年屬于顯著的枯水階段，1978-1994年屬于平水階段，1995-2008年屬于顯著的豐水段，2009-2017年屬于平水階段。枯水持續時間大于豐水持續時間。在年內變化中，一般8月徑流量最大，平均達到500 m3/s，2月或3月徑流量最小，一般僅為27 m3/s，其余月份一般在100 m3/s以上。庫瑪拉克河流域分布如圖1所示。

圖1 庫瑪拉克河流域分布

2.2 模型建模

把庫瑪拉克河1993-2016年的徑流量數據作為樣本，對未來庫瑪拉克河2020-2029年的徑流量進行預測。總體樣本徑流量序列如式（1）所示。由原始徑流量樣本數據可得樣本均值x—=52.15。為了防止|X(0)-≥5%這種情況的出現，把區間大小定為5.00＜0.1=5.22。根據徑流量樣本數據的特征，把樣本數據分為5個區間，即A1=[36.98,45]、B1=[45,50]、C1=[50,55]、D1=[55,60]、E1=[60,69.55]。同時，把徑流量對應的時間作為樣本，得到時間樣本A2、B2、C2、D2、E2。徑流量樣本和時間樣本如圖2所示。

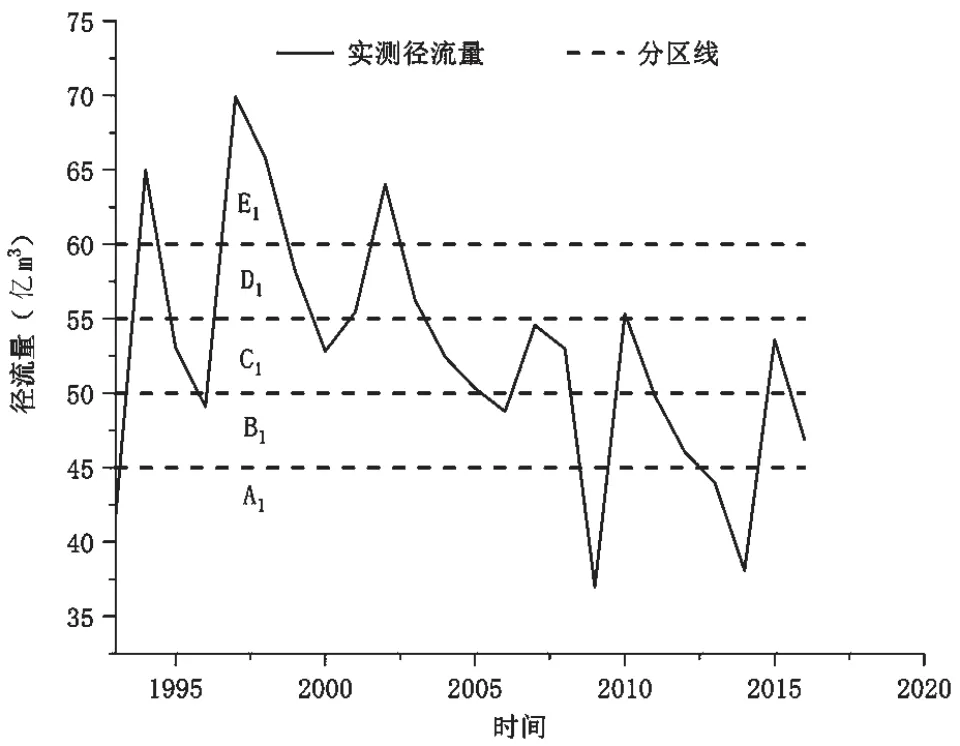
圖2 實測數據區域劃分

根據5個時間樣本的周期性預測和徑流量樣本的趨勢性預測，可以得到10個GM(1,1)函數，并進行模型精度檢驗，模型精度級別=Max{C所處級別，P所處級別}[12]，檢驗結果如表2所示，10個GM(1,1)函數中，80%的預測模型精度達到優秀。優化后的GM(1,1)平均誤差為0.98億m3，相對誤差為2.1%，傳統GM(1,1)的平均誤差為4.65億m3，相對誤差為9.1%。根據《水文情報預報規范》（SL 250—2000），誤差在允許范圍內[15]。

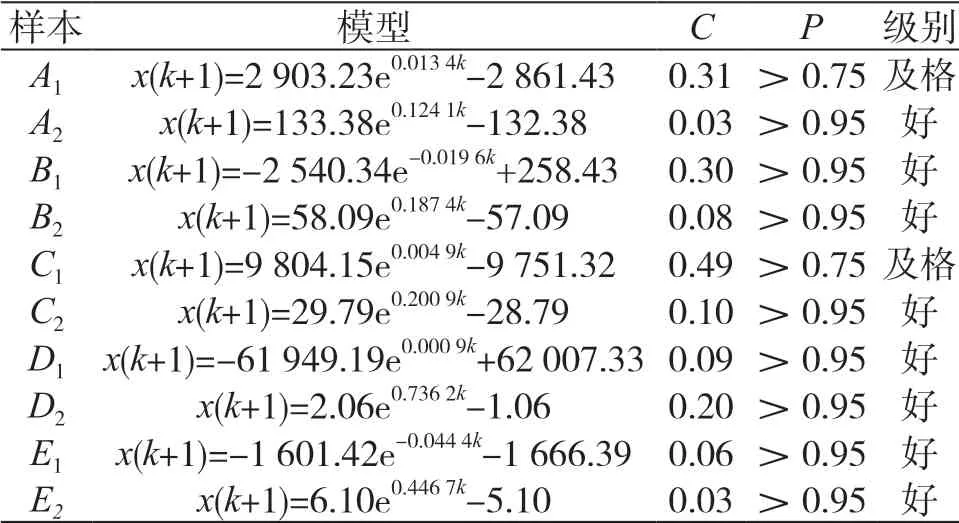
表2 預測模型及精度檢驗

3 結果與分析

3.1 預測結果

采用優化的GM(1,1)對庫瑪拉克河2020-2029年徑流量進行預測，預測結果保留了原始數據的震蕩性和趨勢性。預測數據顯示，豐水年出現在2025年（60.87億m3），枯水年出現在2021年、2024年、2026、2029年（41.32億m3、41.88億m3、44.7億m3、42.44億m3）。庫瑪拉克河2020-2029年徑流量預測結果如表3所示。

表3 庫瑪拉克河預測結果

3.2 模型結果對比分析

把優化GM(1,1)、傳統GM(1,1)、灰色拓撲模型的1993-2016年預測數據與實測數據對比，優化后的GM(1,1)預測結果與實測徑流量的擬合度高于傳統GM(1,1)和灰色拓撲模型。傳統GM(1,1)在1994年以后呈現減函數的趨勢和灰色拓撲波形后移的現象。由此可得，優化后的GM(1,1)與傳統的GM(1,1)和灰色拓撲模型相比更加適合徑流量的預測。優化后的GM(1,1)、傳統GM(1,1)、灰色拓撲模型的1993-2016年預測數據與徑流量實測數據對比如圖3所示。

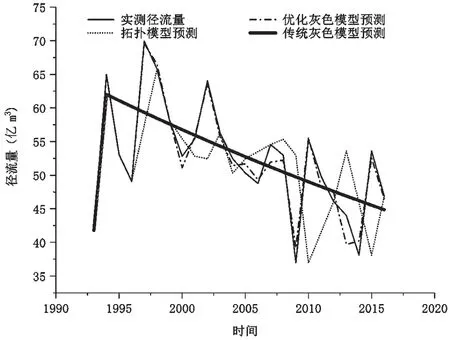
圖3 模型預測數據與實測數據對比

將2017年、2018年、2019年的優化GM(1,1)、傳統GM(1,1)、灰色拓撲模型的預測結果與實測徑流量做對比，對比結果如表4所示。優化后的GM(1,1)具有較好的模擬效果，相對誤差為5%，遠低于傳統的GM(1,1)（相對誤差10.3%）和灰色拓撲預測（相對誤差20.7%）。2017-2019年的實測與預測徑流量做對比，優化后的GM(1,1)精度高于傳統的GM(1,1)和灰色拓撲預測。

表4 各模型預測結果對比

4 結論

本文以新疆庫瑪拉克河協合拉水文站1993-2016年實測徑流量數據為基礎，采用優化的GM(1,1)對該河流2020-2029年徑流量進行預測。結果表明，優化的GM(1,1)預測結果平均誤差為0.98億m3，相對誤差為2.1%，符合水文預報規范要求，且優于傳統的GM(1,1)預測結果（平均誤差4.65億m3，相對誤差9.1%）。同時，把2017年、2018年、2019年預測結果與實測結果做對比，優化后的GM(1,1)精度高于傳統GM(1,1)和拓撲模型。庫瑪拉克河在未來10年中出現4個枯水年（2021年、2024年、2026年和2029年），豐水年出現在2025年，豐水年占比遠低于枯水年，因此地區要提前做好水資源規劃及相關政策應對未來10年可能出現的水資源短缺現象。試驗證明，這種方法更適用于徑流量預測，但是本次研究只考慮了徑流量的多年變化規律，未在模型中考慮地形、環境、天氣等因素對徑流量的影響，要加強這方面的研究。