將信息技術(shù)融入數(shù)學課堂，使數(shù)學核心素養(yǎng)落地生根

金芬

摘 要：要改進“一支筆一塊黑板一張嘴”的教學現(xiàn)狀，突破“意會”與“言傳”的交流障礙，實現(xiàn)數(shù)學課堂教與學的良性互動，高中數(shù)學課堂教學離不開現(xiàn)代教育技術(shù)的支持和助力。筆者以GeoGebra為例，在新教材的課堂教學中，注重將GeoGebra與數(shù)學課程深度融合，通過直觀的圖形或動態(tài)的運動規(guī)律，總結(jié)、猜想、證明新的發(fā)現(xiàn)，把那些“看不透”、“說不清”的一些性質(zhì)通過動態(tài)形式呈現(xiàn)出來，使其清晰可見。實現(xiàn)教學的可視化，為學生理解概念創(chuàng)設(shè)情境，為學生聯(lián)系多元表征發(fā)展數(shù)學學力，為學生實驗探究提供優(yōu)質(zhì)資源。

關(guān)鍵詞：信息技術(shù);GeoGebra;數(shù)學課堂教學;數(shù)學核心素養(yǎng);探究

1.將現(xiàn)代教育技術(shù)融入數(shù)學課堂教學的必要性和重要性

直擊當下數(shù)學課堂，一邊是面對“如何實施核心素養(yǎng)導向的數(shù)學教學？”、“如何才能使學生的數(shù)學學科核心素養(yǎng)得到良好的發(fā)展？”、“怎樣才是教好數(shù)學？”等關(guān)鍵性問題，而一邊是數(shù)學固定的高度抽象性的高冷，使得學數(shù)學的人“望而卻步”，不知如何去意會，教數(shù)學的人使出“渾身解數(shù)”，不知如何去言傳。面對這種尷尬的局面，需要教師對數(shù)學課堂教學進行變革，改進“一支筆一塊黑板一張嘴”的教學現(xiàn)狀，突破“意會”與“言傳”的交流障礙，實現(xiàn)數(shù)學課堂教與學的良性互動，高中數(shù)學課堂教學離不開現(xiàn)代教育技術(shù)的支持和助力。

作為教師要將現(xiàn)代教育信息技術(shù)恰如其分地融入到數(shù)學課堂上。例如，能將復雜問題簡單化，動態(tài)問題靜態(tài)化，抽象內(nèi)容可視化等，有效改革數(shù)學課堂教學，實現(xiàn)優(yōu)質(zhì)教育資源的共享，提高數(shù)學教學質(zhì)量和效益，有效提升學生數(shù)學核心素養(yǎng)。

筆者以GeoGebra為例，在新教材的課堂教學中，注重將GeoGebra與數(shù)學課程深度融合，通過直觀的圖形或動態(tài)的運動規(guī)律，總結(jié)、猜想、證明新的發(fā)現(xiàn)，把那些“看不透”、“說不清”的一些性質(zhì)通過動態(tài)形式呈現(xiàn)出來，使其清晰可見。不僅能充分激發(fā)學生的探究熱情，提高學生課堂的參與度，還能把課堂上高冷的數(shù)學轉(zhuǎn)化為學生充滿激情的探索，使學生的核心素養(yǎng)真正落地生根。

2、 基于GeoGebra的“數(shù)學可視化”，助力數(shù)學課堂教學

GeoGebra這款軟件實現(xiàn)了構(gòu)建“抽象的數(shù)”與“可見的形”之間的聯(lián)系通道，讓學生在數(shù)學課堂上既可以看到“背后”的數(shù)據(jù)，更“看透”其中的數(shù)學內(nèi)容，為學生理解概念創(chuàng)設(shè)情境，為學生聯(lián)系多元表征發(fā)展數(shù)學學力，為學生實驗探究提供優(yōu)質(zhì)資源。

2.1創(chuàng)設(shè)靈動情境，助力概念生產(chǎn)

案例1：函數(shù)y=Asin（ωx+?）

根據(jù)新教材的理念，首先要讓學生理解用函數(shù)模型y=Asin（ωx+?）來刻畫一般的勻速圓周運動，并理解A，ω，?的特定的實際意義，讓學生體會數(shù)學源于生活的本質(zhì)和學習函數(shù)y=Asin（ωx+?）的必要性。于是創(chuàng)設(shè)圖1所示的可視化實驗情境，模擬筒車運動過程實景，抽象出其中的幾何對象與幾何關(guān)系，并動態(tài)分析圓周運動、解析式變換與圖像變換之間的多重關(guān)聯(lián)，利用GeoGebra可進行直觀、動態(tài)、關(guān)聯(lián)地呈現(xiàn)，可以有效地降低教學難度。

其次，在研究參數(shù)A，ω，?對函數(shù)y=Asin（ωx+?）圖像地影響，以及函數(shù)y=Asin（ωx+?）圖像的變換過程時，可事先提供互動性的實驗平臺（圖2），以便學生進行自主的實驗操作、觀察分析、思考探究。學生可以任意輸入?yún)?shù)A，ω，?的值，側(cè)重兩個角度觀察與分析：一是從圓周運動的實際意義看質(zhì)點的運動變化，二是從相應函數(shù)圖像上點的坐標變化看圖像的變換。

從上例可以發(fā)現(xiàn)，數(shù)學概念的掌握需要經(jīng)歷直觀到抽象再到應用的過程，借助強大的現(xiàn)代教育技術(shù)GeoGebra可以創(chuàng)設(shè)直觀靈動的情境，對認知難度大，抽象的概念進行可視化教學，在學生腦中建立豐富的概念模型，經(jīng)歷概念產(chǎn)生的加工全過程，因概念的充分加工和領(lǐng)悟而保證深刻的理解。

2.2聯(lián)系多元表征，助力本質(zhì)理解

案例2：一類旋轉(zhuǎn)翻折問題的探究

立體幾何翻折問題是將平面圖形經(jīng)過翻折變成了空間幾何體，從而考查空間中點、線、面之間的相互關(guān)系，或角度與距離關(guān)系。立體幾何的翻折問題背景簡單，立意深遠，對學生的空間想象能力要求很高。學生在學習過程中容易受立體幾何的思維定勢，無法構(gòu)造空間立體幾何直觀圖，將空間問題平面化的能力缺乏，找不到合理的解決模型將動態(tài)問題靜態(tài)化。因此作者使用GeoGebra軟件設(shè)計課堂教學，通過介紹旋轉(zhuǎn)翻折圓錐模型，也可以總結(jié)為一線五結(jié)論模型，來解決立體幾何中的旋轉(zhuǎn)翻折問題。

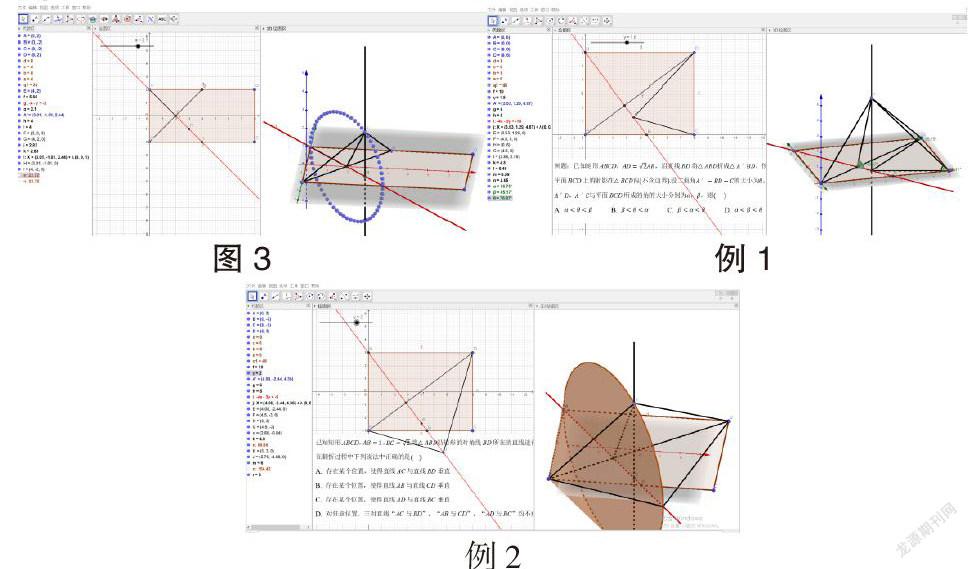
作者先通過一個例子來引出將平面圖形沿折痕旋轉(zhuǎn)翻折為空間圖形，從而研究空間中的角度、距離、軌跡等問題，并用GeoGebra動態(tài)展現(xiàn)旋轉(zhuǎn)翻折問題（圖3），幫助學生在直觀的動態(tài)中探究問題的本質(zhì)。學生結(jié)合二維繪圖區(qū)和3D動態(tài)展示區(qū)的觀察，立馬得出了一系列的結(jié)論：關(guān)鍵要先畫出垂直于折痕（BG）的線（AI）1、關(guān)注翻折前后的不變量和變量;2、點A/的軌跡為F為圓心，A/F為半徑的圓;3、面A/BG繞折痕BG翻折形成兩個同底圓錐;4、點A/在底面的投影H在線段AI（圓的直徑）上;5、∠A/FA為二面角A/-BG-A的平面角。

例2

接下來教師給學生進行了此類問題的檢測，引用的是高考題和高考模擬題（例1、例2），發(fā)現(xiàn)學生通過以上旋轉(zhuǎn)翻折模型的理解，能輕松將空間問題轉(zhuǎn)化為平面問題。借助軟件的動態(tài)可視性，使學生從外部的多元操作感知走向了內(nèi)部理解的認知，也感受到了數(shù)學的美妙，更體會數(shù)學的真實性，解決問題也就水到渠成。

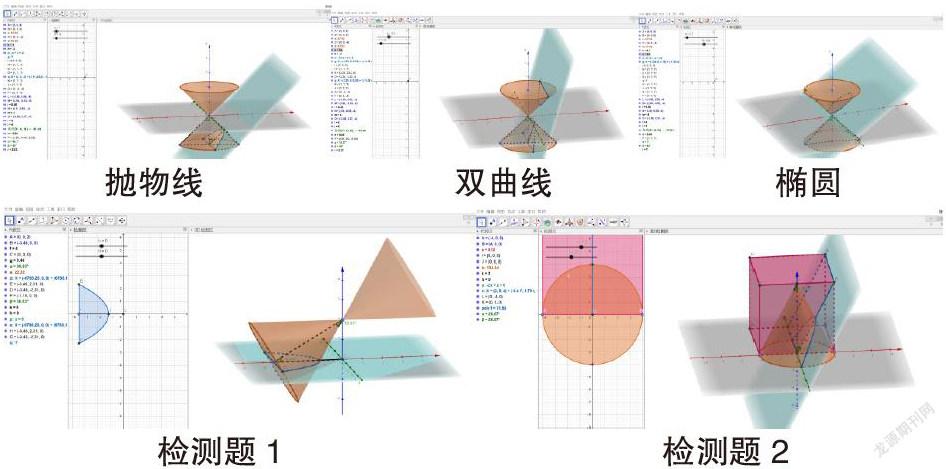
有了以上的探究經(jīng)驗，教師還布置了課外探究活動《一類圓錐截線問題的探究》，讓學生借助GeoGebra軟件解決一類圓錐被不同角度的平面ɑ所截截線形狀問題。學生在學習直線和圓時初步感受了數(shù)形結(jié)合的基本思想，但對圓錐曲線的概念還是僅僅停留在直觀感性認識的層面上;學生在學習過程中也遇到諸多困難：從空間的圓錐截出平面圖形的轉(zhuǎn)化。

學生探究熱情高漲，分別設(shè)計出了以下三條曲線的模型，并總結(jié)結(jié)論：設(shè)軸截面角為α，母軸線角為β則1、α=β時，截線為拋物線;2、α<β時，截線為雙曲線;3、α>β時，截線為橢圓;4、α=90°時，截線為圓，并應用總結(jié)的結(jié)論有效解決了檢測題例1和例2。

2.3自主實驗探究，助力結(jié)論驗證

好的教學方式是激發(fā)學生的好奇心，助力學生在廣袤的數(shù)學世界里探究遨游，鼓勵學生勇敢地去探險，親歷數(shù)學實驗，發(fā)現(xiàn)數(shù)學，而不是簡單的應用數(shù)學解決問題，讓原先高冷抽象的數(shù)學變得生動鮮活起來。學生從直觀想象到猜想、發(fā)現(xiàn)和論證，相互之間進行真正的情感交流和思維碰撞，讓教學走進學生的心靈，在做數(shù)學的過程中豐富感知，在直觀感知中抽象數(shù)學概念。而GeoGebra則可以提供結(jié)論的論證，助力學生的實驗探究，讓學生在實驗探究中深刻思考，心向遠處，行向遠方。

案例3：橢圓、雙曲線的定義

問題1：點A（0，0）和點B（8，0）為兩個定點，圓A是半徑不定的動圓，C是圓上任意一點，線段BC的垂直平方線l和半徑AC相交于點D，當半徑r大于令國人定點距離|AB|時，隨著點C在圓上運動，求點D的軌跡是什么？

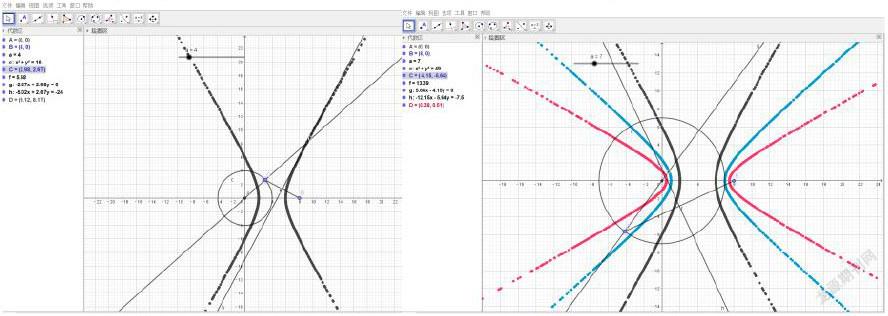
學生通過觀察圖形，發(fā)現(xiàn)幾何關(guān)系|DC|=|DB|，則|DA|+|DB|=r（r>|AB|），學生開始在作業(yè)紙上描點，并不斷地操作，盡量使得到的點D足夠密集，通過觀察散點圖發(fā)現(xiàn)軌跡圖形形似橢圓，但學生依舊感到不確定。教師順勢帶領(lǐng)大家用GeoGebra來驗證實驗結(jié)論是否正確，在繪圖區(qū)內(nèi)畫出圖，將D點設(shè)置為開啟跟蹤，同時C點開啟動畫，此時點D的軌跡呈現(xiàn)出了橢圓的形狀，學生見圖雀躍高呼，教師提出橢圓的定義。

問題2：當r>|AB|時，取r1=12，r2=14，r3=18，時，三個橢圓的形狀會有什么變化？

學生又陷入沉思，通過描點發(fā)現(xiàn)，到兩個定點距離和越大橢圓形狀越扁，教師打開GeoGebra驗證結(jié)論的正確性，并解開學生心中疑慮，提出橢圓離心率的概念。學生親歷了概念生成的全過程，對橢圓的定義了然心中。

教師通過以上的實驗探究論證的過程，鼓勵學生提出更多的問題進行探究，生1：當0<r<|AB|時，點D的軌跡會是什么？大家又再次陷入思考，紛紛畫圖實驗，一段時間后還是一臉茫然，有的學生說是一條類似于反比例函數(shù)的曲線，又有的學生說應該有兩種情況兩條曲線。當大家緊鎖眉頭，有種說不清道不明的滋味時，教師提議：讓GeoGebra來給我們解憂吧！通過演示，得到兩種位置關(guān)系及幾何關(guān)系||DA|-|DB||=r（r<|AB|），在繪圖區(qū)出現(xiàn)了兩條曲線，教師提出雙曲線的定義。追問：當0<r<|AB|時，取r1=4，r2=6，r3=7，時，三條雙曲線的形狀會有什么變化？通過剛才的分析，大家猜測雙曲線的開口有變化，教師用GeoGebra加以直觀演示。

案例4：數(shù)學建模—茶水最佳飲用時間

當我們每隔1min測量一次茶水溫度，收集完六組數(shù)據(jù)時，我們需要對數(shù)據(jù)進行分析，找到溫度與時間的某種函數(shù)關(guān)系，如果能求出函數(shù)關(guān)系式，那么就建立了茶水冷卻函數(shù)模型。大家先將收集的數(shù)據(jù)作出散點圖，通過觀察選擇了反比例函數(shù)和指數(shù)函數(shù)，在GeoGebra里進行擬合并進行誤差分析。

擬合的反比例函數(shù)為y=80.12x-0.12，誤差平方和為3.6995，從圖中可以看出偏離程度較大，當時間x=30時，水溫大概為53.5955℃;而擬合的指數(shù)函數(shù)為y=82.68e-0.05x，從圖中看出各點偏離程度較剛才有點減小，誤差平方和為0.4049，當時間x=30時，水溫大概為19.3737℃.顯然指數(shù)型函數(shù)模型更理想，但是指數(shù)型模型中，當x趨向于無窮大時，趨于0，而實際情況是接近室溫，結(jié)合剛才建立的指數(shù)函數(shù)模型，我們需要對函數(shù)模型進行修正。

學生們開始熱烈地討論，覺得圖像應該要向上平移，使用函數(shù)y=kax+b的函數(shù)模型，此時無法用軟件進行擬合，為了確定其中的字母，學生采用了待定系數(shù)法進行求解，首先得到b=25，當x=0時，y=85，所以k=60，在確定a時，選取了幾個點進行求解，取這些數(shù)的平均數(shù)得到a=0.9227，即得到數(shù)學模型y=60*0.9227x+25，接下來我們對模型進行誤差分析，發(fā)現(xiàn)誤差平方和為0.144，應該是比較理想的茶水冷卻函數(shù)模型。

3、將信息技術(shù)融入數(shù)學課堂教學的反思

作為第一批執(zhí)教新教材的一線教師，需要不斷地提升專業(yè)水平和育人能力，提高數(shù)學教學質(zhì)量和課堂教學效益，轉(zhuǎn)變教學方式，理解現(xiàn)代教育技術(shù)。筆者在必修第一冊和必修第二冊的數(shù)學課堂教學中，嘗試將現(xiàn)代教育技術(shù)GeoGebra融入課堂教學中，取得了較好的成效，在教學過程中反思了幾點，供讀者在接下來的使用中參考。

（1）樹立落實學生核心素養(yǎng)的教學觀

信息技術(shù)的飛速發(fā)展，功能的便捷強大需要我們改變教與學的方式，教師不能一味固守著考試內(nèi)容而不顧學生的核心素養(yǎng)，應合理利用信息技術(shù)讓復雜抽象的學習內(nèi)容變得直觀簡潔，并設(shè)計豐富多樣的數(shù)學實驗平臺，促進學生的探索意識。當然，信息技術(shù)的融入也是對教師的挑戰(zhàn)，需要從學生發(fā)展的角度精心設(shè)計發(fā)現(xiàn)、提出問題的時機，并如何利用信息技術(shù)恰如其分地引導學生親歷整個解決問題的全過程，讓學生感受到左右逢源的體驗感，真正落實學生的數(shù)學核心素養(yǎng)。

（2）平衡好信息技術(shù)融入的度

信息技術(shù)的融入讓教學內(nèi)容變得淺顯易懂，但過度全盤地使用卻會扼殺學生地直觀想象能力，阻礙學生思維能力的提升。學生會對直觀動態(tài)的圖形過度依賴，從而形成思維的惰性，因此，信息技術(shù)的融入教學既要有可視化也要有數(shù)學化，既要實驗猜想也要演繹證明。案例4中，當學生借助GeoGebra得到指數(shù)函數(shù)模型較理想時，還需通過紙筆運算、邏輯推理對模型進行修正，這是信息技術(shù)無法代替的。教師要平衡好信息技術(shù)融入的度，數(shù)學課堂的教學既要“返璞”，也要“歸真”。

（3）信息技術(shù)從融合到創(chuàng)新，讓課堂教學走得更遠

信息技術(shù)融入教學的數(shù)學課堂是集教育技術(shù)、教學內(nèi)容、教學方法三者的深度融合體，而這個融合體是交互的，動態(tài)的生態(tài)系統(tǒng)，需要教師不斷地選擇合適的信息技術(shù)，圍繞信息技術(shù)的特點設(shè)計開放的、靈活的任務，讓學生在豐富多彩、層層遞進的實驗活動中積累原始體驗，并充分發(fā)揮學生的探索力和創(chuàng)造力，讓數(shù)學課堂走向廣度和深度。

參考文獻：

[1]中華人民共和國教育部制定.普通高中數(shù)學課程標準（2017年版）.人民教育出版社

[2]章建躍 李增滬.普通高中教科書教師教學用書.數(shù)學：必修.第二冊：A版.人民教育出版社，2020（12）

[3]唐慧榮.中學數(shù)學可視化教學研究[D].金華：浙江師范大學，2010：6