小學(xué)低年級教學(xué)中模型思想的滲透

盧一凡

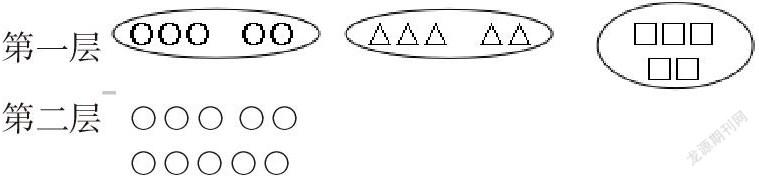
摘 要：小學(xué)低段的學(xué)生能力和心智都處于發(fā)展初期，主要通過直接經(jīng)驗和直觀認(rèn)知獲取知識，教學(xué)中主要采取簡單、直觀的教學(xué)方式，在低段教學(xué)可通過感知、操作、畫圖、聯(lián)想等方式，在教學(xué)中滲透模型思想，構(gòu)建數(shù)學(xué)思維課堂。

關(guān)鍵詞：小學(xué)低年級;模型思想;加法的認(rèn)識

小學(xué)數(shù)學(xué)教學(xué)中，模型思想是教學(xué)中必須滲透的思想方法之一，《義務(wù)教育課程標(biāo)準(zhǔn)》指出：“模型思想的建立是學(xué)生體會和理解數(shù)學(xué)與外部世界聯(lián)系的基本途徑、建立和求解模型可以提高學(xué)習(xí)數(shù)學(xué)的興趣和應(yīng)用意識。”新課改明確提出：數(shù)學(xué)建模過程必須有學(xué)生的主體參與，也就是說它是在學(xué)生自主理解、建構(gòu)基礎(chǔ)上的模型，不再是生硬地塞給學(xué)生的公式、法則等。教師作為學(xué)生的引導(dǎo)者，教授知識的同時也要關(guān)注學(xué)生的年齡特點和思維發(fā)展情況。小學(xué)低段的學(xué)生，他們的年齡大約是6～10歲，能力和心智都處于發(fā)展初期，他們好奇、好動、喜歡模仿，并且有直觀、具體、形象等思維特點，主要通過直接經(jīng)驗和直觀認(rèn)知獲取知識，因此，低段教學(xué)主要采取簡單、直觀的教學(xué)方式，讓學(xué)生有切身體會，慢慢引導(dǎo)學(xué)生理解知識，如何在低段教學(xué)中滲透模型思想呢？下面以北師大版數(shù)學(xué)一年級上冊第二單元《加與減（一）》的第一課《一共有多少》為例，進行初步的探討。

一、情境演示，提出問題，感知模型

低年級學(xué)生注意力的集中能力較差，他們能觀察具體形象的事物，而不善于觀察抽象、概括的材料;能集中注意力于事物的外部現(xiàn)象，而不善于專注于事物的本質(zhì)聯(lián)系。在低段學(xué)生的學(xué)習(xí)中，教師創(chuàng)設(shè)充滿童趣而又有數(shù)學(xué)含量的動態(tài)化情境，能有效激發(fā)學(xué)生的學(xué)習(xí)興趣，促進學(xué)生用數(shù)學(xué)的眼光關(guān)注情境，用數(shù)學(xué)思維理解情境，進而利用感知初步體驗?zāi)Ｐ偷囊饬x。例如，在 “一共有多少”一課中以教師演示、學(xué)生感知開展學(xué)習(xí)。

師（示范）：老師今天帶來一些鉛筆。仔細(xì)觀察，說說老師是怎么做的。

生1：老師一只手拿了3只鉛筆，另一只手拿了2只鉛筆，然后把兩只手里的鉛筆合在了一起。

師：根據(jù)剛才的動作，你們能提出一個數(shù)學(xué)問題嗎？

生1：一只手拿3支鉛筆，另一只手拿2支鉛筆，合起來有5支鉛筆。

師：你用“合起來”來描述，很清楚，但提問題是不能把答案提前告訴大家的哦。誰再來試試？

生2：一只手拿3支鉛筆，另一只手拿2支鉛筆，合起來有多少支鉛筆？

師：你能正確提出數(shù)學(xué)問題了 ！你們都說到這個詞，合起來是什么意思？

生1：“把它們加在一塊兒。”

生2：“把所有的放在一起數(shù)。”

生3：用手比劃，合在一起。

師：用動作表示真形象，在數(shù)學(xué)中更規(guī)范的數(shù)學(xué)語言是“一共”，我們一起來用“一共”這個詞再把這個數(shù)學(xué)問題說一說。

“有多少支鉛筆”這個情境，為學(xué)生提供了多樣的加法原型支撐，情境的動態(tài)呈現(xiàn)為學(xué)生所學(xué)知識與生活之間搭建橋梁，把抽象的加法問題具體化，豐富了學(xué)生對加法模型的感性認(rèn)識。學(xué)生通過用簡潔、準(zhǔn)確的數(shù)學(xué)語言進行表達，來理解具體情境的加法原型。通過語言表征、動作表征，學(xué)生更具體地感知加法的含義，為構(gòu)建加法模型奠定了基礎(chǔ)。

二、直觀操作，探究算法，形成表象

操作是學(xué)生智力的源泉和思維的起點，有效操作能調(diào)動學(xué)生多種感官參與認(rèn)知活動，提高學(xué)習(xí)效率。教師應(yīng)在操作探究的基礎(chǔ)上，發(fā)展學(xué)生的數(shù)學(xué)思維能力，使學(xué)生對數(shù)學(xué)模型思想的感悟更形象、更深刻。例如，在 “一共有多少”的教學(xué)中開展“數(shù)一數(shù)”的活動。學(xué)生對數(shù)的認(rèn)識是在數(shù)數(shù)的過程中發(fā)展起來的。數(shù)數(shù)是學(xué)生學(xué)習(xí)加減法運算的基礎(chǔ)，也是探索計算方法的起始。

師：老師一只手拿3支鉛筆，另一只手拿2支鉛筆，一共有多少支鉛筆？數(shù)一數(shù)。

生：5支。

師：大家怎么數(shù)出來的？拿出你的小棒或者小圓片，和你的同桌說一說！

生1：一支一支地數(shù)出來的。

師：有不一樣的數(shù)法嗎？

生2：我是從3開始數(shù)的。（一只手指著教師手中 的3支鉛筆，數(shù)出3，接著數(shù)另一支手中的4、5）

師：你為什么要從3數(shù)起呢？

生2：因為我已經(jīng)知道這邊有3支，我就接著從3 數(shù)起。

師：和前面那位同學(xué)從1數(shù)到5相比，大家喜歡 哪一種數(shù)法？為什么？

生：喜歡第2種數(shù)法，從3往后數(shù)更快些。

這個活動中，充分利用學(xué)生數(shù)數(shù)的經(jīng)驗將數(shù)的認(rèn)識與數(shù)的運算有機結(jié)合，學(xué)生充分經(jīng)歷了動手操作、自主探究的過程，在數(shù)的過程中體會計算方法，體驗加法運算的意義，形成加法模型的表象。

三、畫圖表征，揭示本質(zhì)，內(nèi)化模型

低年級的學(xué)生對一些抽象的文字，符號的理解可能有一些困難，教師給學(xué)生講解題目時，常常發(fā)現(xiàn)千言萬語都抵不上一個圖示。畫圖策略是非常重要的一種分析問題和解決問題的策略，它是利用“圖”的直觀來對問題中的關(guān)系和結(jié)構(gòu)進行表達，可以使復(fù)雜數(shù)學(xué)問題變得簡明、形象，促使學(xué)生直接地理解數(shù)學(xué)，從而幫助學(xué)生分析問題和解決問題。如果課堂適時地讓他們自己在紙上涂一涂、畫一畫，可以拓展學(xué)生解決問題的思路，幫助他們找到解決問題的關(guān)鍵。可以說，圖形在學(xué)生數(shù)學(xué)模型建立的過程中發(fā)揮著重要作用。

例如，在“一共有多少”中，學(xué)生通過“畫一畫”，更深刻地理解加法合并的意義，從而抽象出加法模型。

師：“如果不用學(xué)具，你能在紙上畫一畫表示一共有多少鉛筆嗎？”

學(xué)生做法如下：

嘗試讀懂的過程中，先出示第一層的方法。讀懂每種方法后，進行探討。

師： 這三種方法有什么相同的地方嗎？

生：都有3、2兩部分，都畫了一個大圈

師：大圈表示什么意思？

生：大圈表示兩部分合起來五支鉛筆

師出示第二層：這些方法與剛才的三種方法有什么不同嗎？

生：之前的方法有個大圈圈，這幾個沒有。

師：你認(rèn)為要不要畫個圈呢？

生：需要，這樣就把這兩邊的放一塊了，不然是兩塊兒（兩個獨立部分）。

寫一寫、畫一畫的過程就是一個“去情境化”的過程，它能夠幫學(xué)生把情境中的數(shù)量關(guān)系進行提煉，并且進行直觀表達。學(xué)生借助圖形表示“合起來”、理解畫圖中 “合起來”的表示方法，思維過程由具體到逐步抽象，從動作思維發(fā)展到形象思維。學(xué)生利用符號去思考，積累了活動經(jīng)驗，培養(yǎng)了初步的符號意識，促進他們的數(shù)學(xué)思考，對于接下來引入數(shù)學(xué)加號、建立加法模型起到了很好的鋪墊作用。

四、聯(lián)想應(yīng)用，抽取共性，建立模型

小學(xué)生形成數(shù)學(xué)概念一般要經(jīng)過“直觀感知一建立表象一揭示本質(zhì)屬性”三個階段。直觀感知和建立表象是建立概念的基礎(chǔ)，概念本質(zhì)屬性的揭示是概念教學(xué)的關(guān)鍵。在此基礎(chǔ)上引岀模型概念，聯(lián)想應(yīng)用到生活中，建構(gòu)模型就可以水到渠成。例如，在 “一共有多少”一課中

師：一共有多少只鉛筆，是把3和2合起來得到5，怎樣用算式表示呢？

生（齊）：3+2 = 5。

師（板書）：誰能說一說，這里的3、2、5分別表示什么？

生，：3表示一只手里有3支鉛筆，2表示另一只手里有2支鉛筆，合起來一共有5支鉛筆。

師：把兩個部分合起來就要用加法。你還能找到一些用“3+2 = 5”來解決的數(shù)學(xué)問題嗎？

生1：桌子上有3塊橡皮，又拿來2塊橡皮，一共有多少塊橡皮？

生2：停車場里有3輛汽車，又開來2輛汽車，一共有多少輛汽車？

生3：教室左邊墻上有3幅畫，右邊有2幅畫，一共有多少幅畫？

生4：我有2本課外書，媽媽又買回來3本，一共有多少本課外書？

師：剛才同學(xué)們提出的這些問題，有的是求一共拿了幾塊橡皮，有的是問一共來了幾輛汽車，有的是問一共有多少幅畫，還有的是說一共有幾本課外書， 為什么它們都可以用“3+2”來解決？

生5：雖然說的事情不一樣，但都是把3個和2個合起來，所以都可以用“3+2 = 5”來表示。

“一共有多少塊橡皮”“一共有多少輛車”“一共 有多少本課外書”等，學(xué)生尋找到這些生活原型，說明他們已經(jīng)將身邊的事物與加法概念聯(lián)系在一起， 意識到了“3+2 = 5”是對許多生活事例的提煉。此時，教師的有效追問：“為什么它們都可以用3+2來解決？”促進學(xué)生提升了思維，內(nèi)化了合并的含義，建構(gòu)了加法模型。

對于模型的構(gòu)建，引導(dǎo)學(xué)生經(jīng)歷對直觀模型操作的動作表征、語言表征、畫圖表征和符號表征的全過程，發(fā)展符號意識，學(xué)生經(jīng)歷模型的產(chǎn)生與提煉的過程，不僅幫助學(xué)生真正理解模型蘊含知識的意義，同時也為學(xué)生模型思想的建立奠定基礎(chǔ)。總之，在教師的日常教學(xué)中，需要認(rèn)真發(fā)掘教材內(nèi)容中隱含的數(shù)學(xué)模型思想，把它滲透到備課中，滲透到學(xué)生思維過程中，滲透到知識形成的過程中，滲透到課堂小結(jié)中，滲透到學(xué)生作業(yè)中，使學(xué)生在探究學(xué)習(xí)中滲透數(shù)學(xué)模型思想。教師要有意識地滲透數(shù)學(xué)模型思想，讓學(xué)生在知識的探究過程中去感知了解、操作體驗、畫圖分析、聯(lián)想應(yīng)用，提高學(xué)生的數(shù)學(xué)素養(yǎng)。

參考文獻：

[1]郭海娟.聚焦活動體驗 提煉模型思想[J].小學(xué)教學(xué)參考： 數(shù)學(xué)版，2014（ 1） ： 62.

[2]張曉玲.淺談小學(xué)低段數(shù)學(xué)教學(xué)[J].儷人： 教師，2015（ 20） ： 26.