再生混凝土抗壓強度預測方法研究★
羅 巍,王浩然,甘凱元,譚靜雯,溫宇嘉
(廣西大學土木建筑工程學院,廣西 南寧 530004)
1 概述
再生混凝土[1]是一種以廢棄混凝土塊進行加工、破碎、分級,按一定比例與級配混合制成再生骨料,用于替代混凝土中部分天然骨料的綠色環保材料,其是解決如今天然骨料日益匱乏和建筑垃圾污染問題的措施之一。由于廢棄混凝土來自于各種途徑,再生骨料性能有較大的離散性,對于確定再生混凝土強度范圍需要大量的實驗,過程煩瑣且成本較高。隨著如今人工神經網絡研究取得了飛速進展,誤差反向傳播算法(BP算法)理論的出現給諸多研究領域的發展帶來了新的契機。BP算法的理論基礎是梯度下降法,尤其擅長解決相互關系較為復雜的多種因素共同作用的非線性問題,但由于網絡初始權值和閾值一般為隨機選取,導致網絡收斂時易陷入局部最小值。遺傳算法[2]是由美國的Holland教授在1962年提出的采用進化論規則建立起的并行隨機搜索最優化方法,該方法能利用其較好的全局搜索能力取代BP神經網絡局部搜索的缺陷,現在已被人們廣泛的應用于機器學習、組合優化以及其他學科科研領域等。因此本文使用Matlab建立了GA-BP神經網絡再生混凝土預測模型,從其他論文中收集了60個再生混凝土配合比數據用于神經網絡訓練與預測,通過對比GA-BP神經網絡和BP神經網絡的預測結果,驗證GA-BP神經網絡的可靠性。
2 GA-BP預測模型原理
BP(Back-Propagation)神經網絡是人工神經網絡中應用最廣泛的網絡模型,其能建立輸入與輸出之間的非線性函數,較好的模擬兩者之間的關系。其原理是模擬生物大腦的響應機制建立拓撲網絡結構,模擬神經沖突的過程,信號向前傳遞到輸出層,再進行反向傳播,不斷調整網絡的權值與閾值,直到預測輸出逼近期望輸出為止。
遺傳算法的原理是將個體信息轉變為計算機可識別信息,用適應度函數評估每一個個體的優良程度后,通過選擇,交叉,變異的操作,在種群的迭代中不斷篩選出更優的個體。將優化后個體的初始權值與閾值賦予BP神經網絡可以較好的改善網絡的預測性能。將遺傳算法用于BP神經網絡,構成新的GA-BP神經網絡,可以充分發揮遺傳算法的全局搜索能力。GA-BP神經網絡工作原理見圖1。
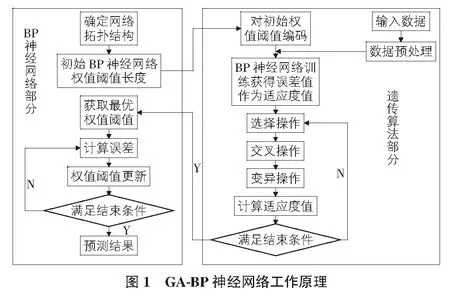
3 模型建立
3.1 BP神經網絡結構確定
通過查閱大量文獻,對再生混凝土抗壓強度具有影響的因素進行篩選,本模型采用水泥、粉煤灰、細骨料、粗骨料、再生粗骨料、減水劑、水膠比作為輸入量,將上述7個變量作為輸入向量,抗壓強度作為輸出向量。已有理論證明,一個三層BP神經網絡就能實現以任意精度逼近目標的非線性問題,因此選擇單隱含層可以提高運算效率。由于BP神經網絡結構相關研究理論還不夠成熟,如今隱含層神經元個數仍沿用經驗公式確定。本文根據Hecht-Nielsen提出的經驗公式確定神經元個數約為15個,經過試算確定網絡神經元個數為15個時網絡預測效果最佳。BP神經網絡拓撲結構如圖2所示[3]。
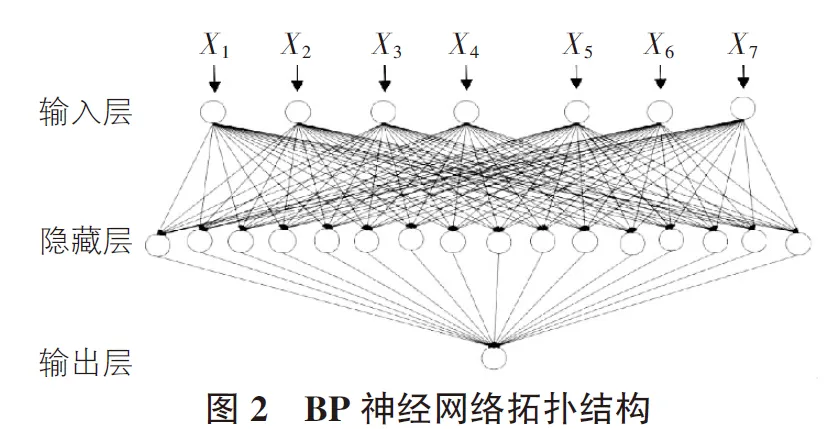
3.2 訓練方案
BP神經網絡的訓練大致分為數據歸一化、傳遞函數選擇、訓練函數選擇和其他參數設置4個步驟。
1)為了消除因數量級差異引起的系統誤差,以及滿足傳遞函數的使用條件要求,需要對收集到的數據進行歸一化處理。本研究使用matlab提供的歸一化函數mapminmax。
(1)
2)傳遞函數也稱激勵函數,其控制著神經網絡中輸入輸出層的關系。常用的傳遞函數有purelin,logsig,tansig函數。對以上幾種函數進行組合測試,發現輸入層與隱含層間采用logsig函數,隱含層與輸出層間采用tansig函數的組合,網絡性能更優。因此本模型選擇logsig-tansig函數組合。
3)訓練函數是確定調整的大算法,負責調整全局的權值與閾值。查閱大量相關資料根據經驗得出,采用訓練函數為trainlm的Levengerg-Marqardt訓練方法收斂速度快,訓練時間短,精度高。本模型采用trainlm訓練函數。
4)BP神經網絡的運算表現可通過對網絡的迭代次數、學習速率、目標誤差進行合適的設置提高運算精度。網絡的迭代次數在超過10 000次時BP神經網絡誤差不再降低,選擇合適的迭代次數能縮短程序運行的時間,本文取迭代次數為2 000次。學習速率決定網絡每一次權值的變化量,數值過小會導致較長的訓練時間,數值過大則會引起系統的不穩定性,一般學習速率合理的取值在0.01~0.8,本文選取學習速率為0.01。網絡訓練的目標誤差設置為0。
3.3 遺傳算法優化
在一個完整的BP神經網絡個體中,包含輸入層到隱層的權值,隱層的閾值,隱層到輸出層的權值,輸出層的閾值,將這些特征值進行編碼,就可以將個體轉化成可識別信息,本文采用常用的實數編碼,染色體長度為numsum=7×15+15+15×1+1=136。
遺傳算法優化工作主要涉及以下兩方面的內容:
1)適應度函數的選擇。適應度函數是個體適應度的評判標準,用于衡量個體的優劣性。本研究把預測輸出與期望輸出之間的誤差絕對值的和作為個體適應度值,個體適應度值越小,則該個體所代表的BP神經網絡性能越好,本文所用適應度計算公式為:
(2)
2)確定遺傳算子及其他參數。本文選擇操作采用經典的輪盤賭法,即適應度越高的個體被選擇的概率越大。交叉操作采用算數交叉,交叉概率取0.4。變異操作采用非均勻變異,變異概率取0.1。個體數量決定了染色體的多樣性,個體數量過少會導致算法不易找出更優解,個體數量過多則增加了程序運行時長,本文取個體數量為30個。種群迭代次數取60。
4 模型應用
4.1 數據收集
試驗所用的實測樣本來自于陳宇良[4]、念夢飛[5]、王國林[6]、徐芊[7]、徐翔波[8]、孟紅[9]、趙敏[10]等人所做的再生混凝土試驗數據,為了減小神經網絡優化前后對比結果的干擾,經過比對試驗數據所用的原材料和實驗條件的相似性后,共篩選到60組數據。其中,50組數據用于BP神經網絡模型的訓練,10組數據用于模型精度的評價。神經網絡的訓練樣本見表1。
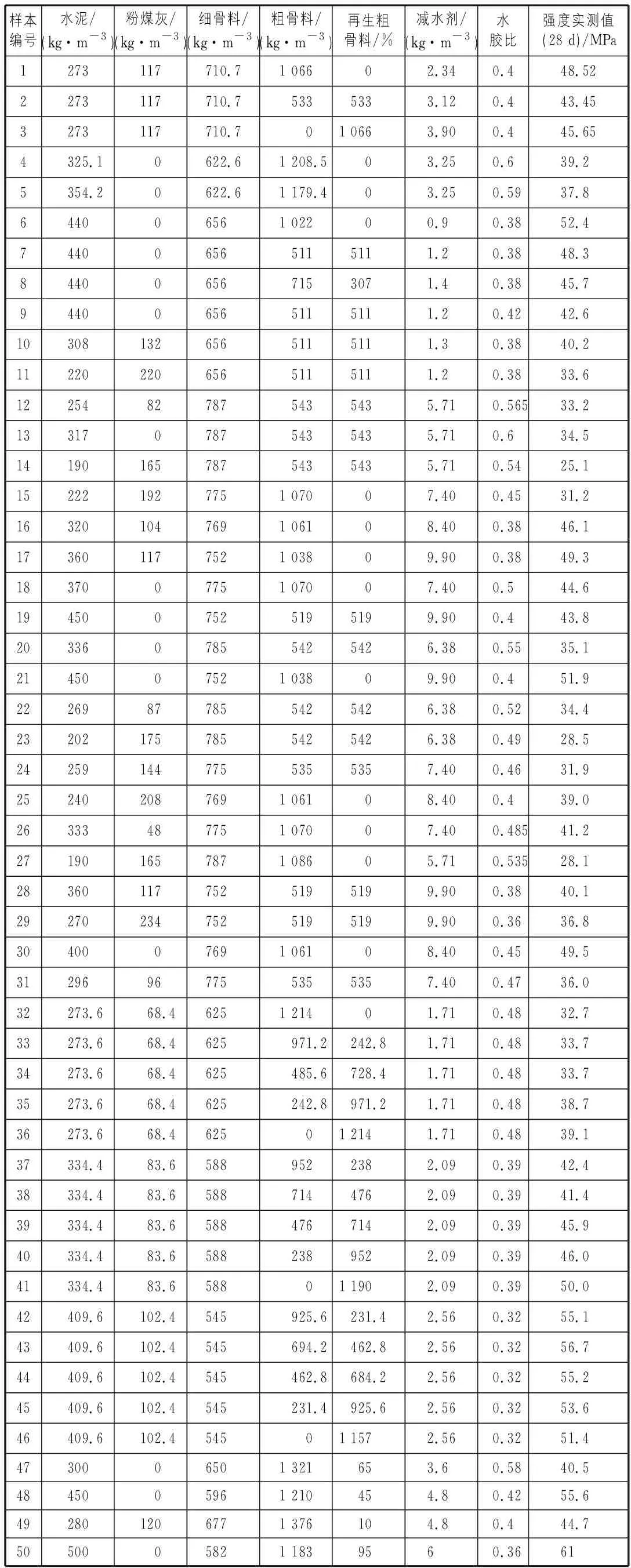
表1 神經網絡訓練樣本(50組)
4.2 網絡測試及結果分析
將同樣的訓練樣本分別代入BP神經網絡與GA-BP神經網絡,設置相同的網絡訓練參數,基于訓練好的網絡代入測試樣本測試。BP神經網絡與GA-BP神經網絡預測結果分別如圖3,圖4所示,GA-BP神經網絡個體的適應度曲線如圖5所示,結果及優化前、優化后誤差相關計算數據見表2。


表2 神經網絡預測結果及誤差(10組)
從圖3可以看出BP神經網絡有較好的預測能力,預測結果和實際強度誤差值在工程誤差需求的范圍,可以應用于再生混凝土的抗壓強度預測。
圖5的適應度曲線說明了隨著種群迭代代數的增加,個體適應度有所提高,初代的個體適應度值為2.868,在迭代至第38代時篩選出了整個迭代循環的最優個體,個體適應度值為1.965,此后個體適應度值不再下降。
通過對比圖3與圖4的預測結果,可以發現GA-BP神經網絡的預測數據整體更接近于期望輸出曲線,曲線預測的變動幅度整體也更加穩定。
由表2的數據可以看到,BP神經網絡和GA-BP神經網絡的預測平均誤差分別為6.9%和4.9%,說明GA-BP神經網絡擬合程度較未優化的BP神經網絡更優,驗證了遺傳算法優化的可靠性。
5 結論
1)根據已有數據建立基于配合比的再生混凝土抗壓強度預測的BP神經網絡模型,證實了BP神經網絡用于再生混凝土強度預測是可行的。
2)當再生混凝土的配合比發生改變時,所建模型可以快速預測抗壓強度,預測結果能夠滿足工程需要。
3)結合遺傳算法程序能較好的優化BP神經網絡的預測性能,網絡預測精度相比傳統BP神經網絡進一步提高。

