充填擋墻受力及變形模擬分析★

曹澤宇,張靜輝,何 偉,劉 臻,任偉成

(1.華北理工大學礦業工程學院，河北 唐山 063210； 2.北京科技大學土木與資源工程學院，北京 100083)

0 引言

在充填工藝中，充填擋墻以不同的結構形式，預先布設在充填空區各個階段的通口內，將充填區與保護區隔離開來，以防止空區充填料漏漿、跑漿[1-5]。其安全、穩定性，對井下工作人員、設備及正常生產是極其重要的安全保障[6-8]。

目前最為常見的設計依據為工程類比法和實踐經驗法，采用軟件模擬的方式分析擋墻受力及變形情況，有助于相關設計人員更準確的選取適用于礦山實際情況的設計理論及方法，避免了擋墻結構不合理，充填中受力過大易倒塌，導致大量砂漿流失，設備損壞、巷道堵塞等情況。

1 充填擋墻模型建立

根據礦山中充填擋墻的實際工程，選取某銅礦空場嗣后充填的充填擋墻尺寸、充填材料及不同充填高度擋墻所受的荷載等參數，運用Plaxis對充填擋墻的正面和側面進行模擬，從而對擋墻的強度和變形等方面進行分析研究[9-11]。

根據該銅礦山采礦方法、礦體厚度以及礦山單位要求，采場沿礦體走向布置，礦房與礦柱交替回采，選取了某充填采空區，長為30 m，寬為20 m，高為60 m。充填擋墻構筑于出礦進路，距離采場邊界約為3 m～5 m，出礦進路尺寸為3.5 m×3 m。

1.1 擋墻側面模型構建

擋墻側面的模型尺寸大小為3.5 m×0.5 m。由于對擋墻側面的變形進行分析，模型選擇平面應變模型，墻面的單元選擇15節點，15節點相比于6節點可以更明顯的表征充填擋墻內部的變化。模型的頂底面采用水平約束，擋墻側面的左邊界根據不同的一次充填高度施加相對應的分布荷載，右邊界設置為固定約束。

墻面的材料參數如表1所示。

表1 墻面的材料參數

充填擋墻側面的幾何模型完成后，需要生成墻面的有限元網格，由于幾何模型的尺寸偏小，所以選擇生成粗網格擋墻側面的墻面有限網格模型，網格如果過細會導致內部的變化無法區分。

1.2 擋墻側面初始條件的確定

在充填擋墻的幾何模型和有限元網格建立好之后，我們必須對擋墻側面的初始應力狀態和初始構造進行確定。由于我們研究一次充填高度的料漿所產生荷載對擋墻面的影響，所以初始條件選擇幾何構造模式，給充填擋墻側面的左邊界施加分布荷載。當充填高度不大于擋墻高度時，擋墻側面模擬一次充填高度1 m,2 m,3 m及墻頂四種情形。由于充填料漿處于不大于擋墻高度的情況，充填料漿表面接觸墻面的水平部分，我們認為其產生的荷載為零，根據靜力學理論，充填料漿的最底面對墻面所產生的荷載最大，給擋墻所施加的分布荷載為線性荷載，根據礦山已有工程選取這四種情形下的最大荷載，如表2所示。

表2 不同一次充填高度的最大荷載

2 模擬理論計算

根據擋墻側面左邊界施加工程中對應的分布荷載，從而去研究擋墻的強度和變形情況，選擇的計算類型是塑性分析，塑性分析根據小變形理論來執行計算。控制參數中的附加步數，按照軟件初始的定義，默認250步，這個步數一般足夠完成計算工序。因為分布荷載是我們根據工程中的參數來確定并且施加的，所以加載類型選擇分布施工。在分布施工窗口中，選定幾何構造模式去激活初始施加的初始條件。當初始條件激活后，便可以對工序進行計算并且輸出相對的擋墻側面模擬結果圖，輸出的結果圖有擋墻的水平位移、總應力、總應變和平均有效應力的模擬結果。

3 充填擋墻模擬分析

3.1 一次充填高度1 m模擬分析

充填高度1 m時，充填擋墻側面的模擬情況如圖1所示。線段的長度代表相對大小，線段的指向代表方向。

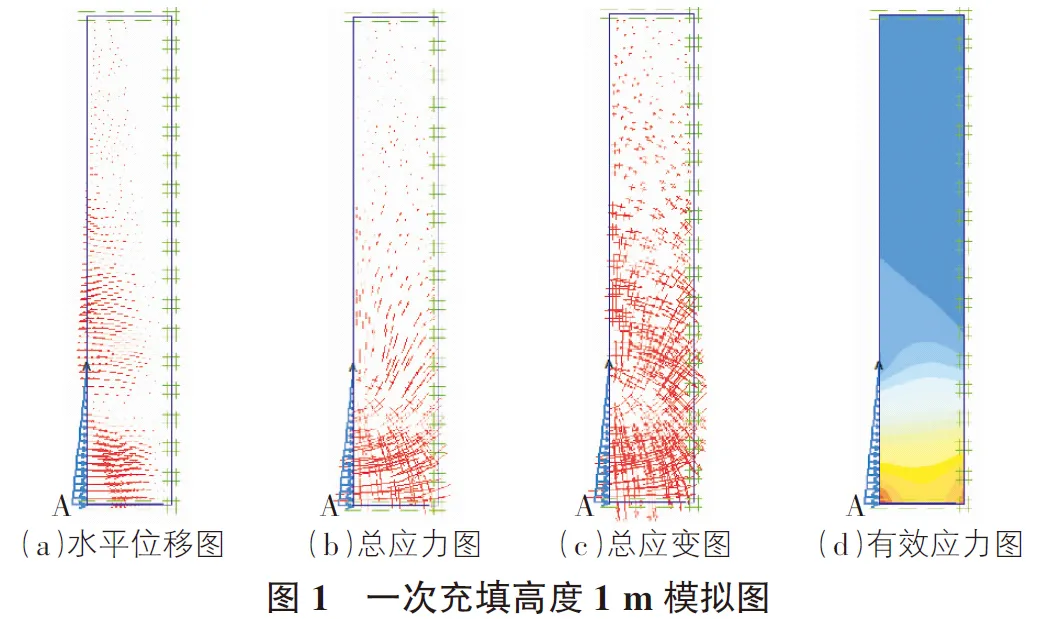
水平位移模擬圖中，充填高度0.6 m以下的擋墻，內部質點有非常顯著的位移，水平位移主要集中在接觸荷載的墻面底部到中間部分，偏靠向墻面的左側。在未充填的高度范圍內，內部的質點也有一定的水平位移，但墻面的位移非常的小。總應力模擬圖中，主要的應力集中在0.6 m以下，相對于其上部的應力，線段的長度和分布的密集程度都大，應力方向指向擋墻的底部。充填高度以上，也存在應力的分布，隨著向上的延長，應力越來越分散且越來越小。在擋墻0.6 m以下，是主要應力集中的區域，在總應變模擬圖中，其內部的應變也是最大的。充填高度以上的小部分區域出現了變形，隨著向上的延深，應變越來越分散且越來越小。平均有效應力模擬圖中，中間部分的應力分布是均勻的，底部墻角的有效應力大于墻體的中間部分，充填的最高處，墻體內部的有效應力上凸，未充填的墻體內部也受到一定影響。

3.2 一次充填高度2 m結果分析

充填高度2 m時，充填擋墻側面的模擬情況見圖2。

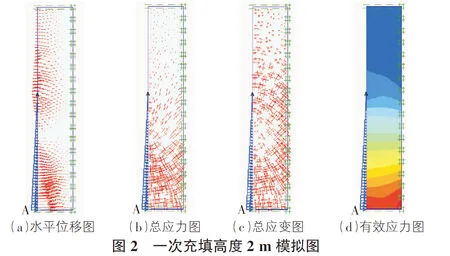
水平位移圖中，充填高度1 m以下的擋墻，內部質點的水平位移最大，集中在荷載作用的墻面這一邊，右側雖然也有水平位移，相對左邊非常的小。荷載接觸的1 m～2 m范圍的擋墻，水平位移非常小。下面充填部分墻體的壓力作用也引起了未充填部分擋墻內部質點的微小水平位移。總應力模擬圖中，主要的應力集中在1.3 m以下，應力的分布程度比較均勻，應力方向指向擋墻的底部。在1.3 m以上高度，隨著向擋墻頂部的延深，應力的分布程度越來越稀疏，而且應力越來越小，應力方向指向擋墻的頂部。總應變模擬圖中的應變變化情形與總應力模擬圖變化一致，在1.3 m以下，應變集中且最大，1.3 m以上，應變隨向上延深而變小。充填部分距底部1.3 m～2 m的范圍，在擋墻未接觸荷載作用的右邊墻面處，應變比同水平上的應變大，總應力圖中，其相對應位置上的總應力也是較大的。平均有效應力模擬圖中，中間部分的有效應力都是呈均勻水平分布的，充填的頂部呈上凸型，充填的底部呈下凹型，未充填的部分墻體也有極小的應力。

3.3 一次充填高度3 m結果分析

充填高度3 m時，充填擋墻側面的模擬情況見圖3。

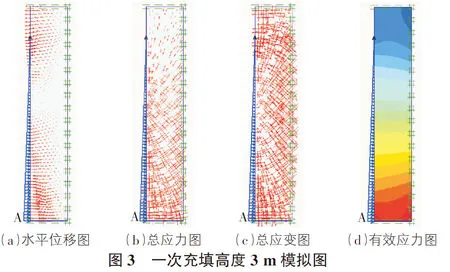
水平位移模擬圖中，1 m以下的擋墻內部質點水平位移最明顯，主要集中在墻體的左側，1 m以上的墻體部分，水平位移非常的小，并且在部分區段位移量幾乎為0，在沒有充填的墻體內部也同樣出現了較小的水平位移。總應力模擬圖中，擋墻高2 m以下，應力的方向指向下面，應力隨著向下延深越來越大，總體的分布比較均勻，擋墻高2 m以上，應力方向指向上面，比2 m以下的應力小很多，隨著向上延深應力減小，未接觸荷載的墻體內部雖有應力，但其數值非常小。總應變模擬圖中，應變從左側2 m～2.5 m墻面處向四周呈射線狀均勻分散，整個墻體內部的應變的大小和應變的密度分布相對均勻，最上面的0.5 m墻體，其內部的應變明顯小于下面接觸荷載的墻體內部的應變。平均有效應力圖中，中間的平均有效應力都是呈水平均勻的分布，只有頂底部的平均有效應力分布特殊。最底面的墻體，兩個墻角出現了有效應力的集中，未充填部分的0.5 m墻體有很小的有效應力出現，但在右側的墻角處沒有平均有效應力。

3.4 一次充填高度到墻頂結果分析

充填高度到墻頂時，充填擋墻側面的模擬情況見圖4。

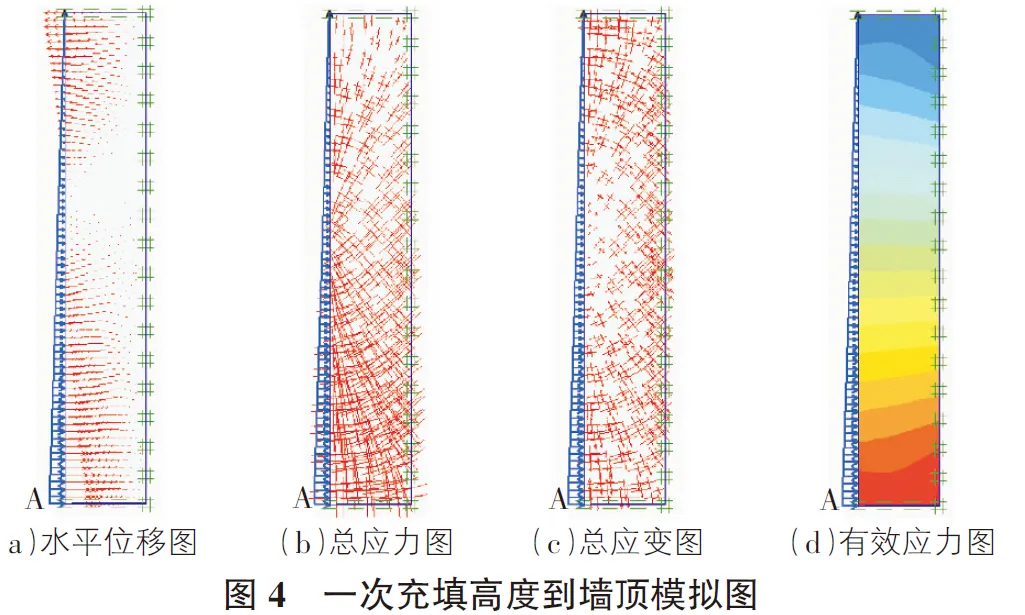
水平位移模擬圖中，水平位移主要集中在擋墻高度的1/2以下，雖然最下面的位移比其他部分的位移大，但其分布程度比較零散，中間部分一小段墻體的水平位移最小，隨著向上的延深，水平位移逐漸變大，但總體情況比墻面最下部的水平位移小很多。總應力模擬圖中，總體來看，應力的分布相對均勻，應力從墻面的底部向上延深逐漸變小，從擋墻一半的高度劃分，上面的應力方向指向擋墻的頂面，下面的應力方向指向擋墻的底面。總應變模擬圖中，整個墻面的應變分布總體均勻，而且比較稀疏。在左側1.5 m～2.5 m墻面處向四周從小到大分散開來，只在接近左側墻面處應變偏小，其余各處的應變大小接近。平均有效應力模擬圖中，有效應力在水平上都是呈均勻分布的，墻體的頂底處，有效應力并未出現墻角集中的現象。

4 結論

本文以某銅礦中充填擋墻的實際工程出發，利用plaxis有限元軟件對一次充填高度1 m,2 m,3 m和到墻頂四種條件下充填擋墻的受力及變形情況進行了模擬分析，得出主要結論如下：

1)最大的水平位移出現在墻體的左下側，此處為最容易發生損壞的地方。一次充填高度未到頂時，未充填部分的墻體也會有微小的位移，隨著高度的增加，未充填部分的位移也明顯增大。一次充填高度小于2 m時，最大的水平位移更加集中，高度大于2 m時，最大的水平位移之間相對分散一些。

2)四種充填高度情形下的結果與靜力學中擋墻受力的結果一致。在一次充填高度的1/2以下，應力最大，且應力分布比較均勻，而且應力的方向也大致在這個區間內進行了劃分，上面的應力方向向上，下面的應力方向反之，并且上面的應力遠遠小于下面。未充填部分的墻體也出現微小的應力。

3)在擋墻的左上側出現一個半圓形的小應變區，然后由半圓向四周均勻的擴散，其余各處的應變大小都相對接近。一次充填高度1 m時，最大應變比其他三種情形的最大應變大很多，并且在充填高度的上面那一小部分墻體，其應變同樣非常的大。