基于信息熵的食品安全事件聚類方法研究

2021-10-05 12:53:40辜萍萍

智能計算機與應用 2021年5期

辜萍萍

(廈門大學嘉庚學院信息科學與技術學院，福建漳州363105)

0 引言

近幾年，中國的食品安全危機成為發展小康社會的絆腳石，主要集中表現在化學添加劑與農藥等濫用、生產流通環節衛生狀況差、安全標準不夠完善、監管水平有待提高幾個方面。2017年2月，國務院印發《“十三五”國家食品安全規劃》文件，明確指出“保障食品安全是建設健康中國、增進人民福祉的重要內容，是以人民為中心發展思想的具體體現”［1］。規劃中制定了針對食品安全管理的基本原則:預防為主、風險管理、全程控制與社會共治。現階段，國家不斷加大整治力度，從完善政府監管體制到增強全民自主防范意識多渠道多維度進行共治，全面打造老百姓可信賴的食品安全環境。

在智能信息化時代背景下，提高食品安全智慧的監管能力、實施“互聯網+”食品安全監管項目、推進食品安全監管大數據資源共享和應用是切實的目標與手段［2］。目前，數據挖掘方法正越來越多地被應用于食品安全相關數據進行知識發現。例如，江蘇省食品安全研究基地的李清光等人運用Hierarchical Cluster方法對2005～2014年間發生的有明確時空定位的2 617起食品安全事件進行聚類分析，總結了事件集的區域分布特點以及隨時間變化的空間轉移趨勢［3］。本研究提出一種基于信息熵的食品安全事件聚類分析模型，對食品安全事件中的相關屬性特征進行提取，從聚類模式中挖掘代表性的問題，分析不同種類食品的各種不安全因素是否受到日期與地區的某種影響，發現各地區之間是否在食品安全危機狀況上存在相似點，從而為監管部門在措施制訂過程中提供決策支持，也為普通消費者在采購食用方面提供信息參考。

1 食品安全數據挖掘的意義

數據挖掘中的聚類分析、關聯規則、決策樹及偏差檢測等技術在食品行業管理領域不斷被應用及推廣，利用這些挖掘技術找出潛藏在數據中的知識，為監管及預防提供依據。其意義主要體現在以下2方面:

（1）數據挖掘技術用于食品安全事件數據的分析，可以發現事件發生的特點、規律以及未來發展趨勢，對監管部門分析事件發生的原因、制定監管措施，更有效地預防事件的發生都存在積極的作用，從而利于社會的安定與發展。

（2）通過公眾媒體渠道發布數據挖掘的相關結果，讓民眾了解食品安全事件中更深層次的信息，提醒民眾結合平時的采購及飲食習慣，警惕可能存在問題的食物，遠離風險源頭，保障自身的飲食健康。

2 數據采集與建模

2.1 食品安全數據的采集

無論是食品生產環境受到污染還是制造過程的非法添加，近些年食品安全事件層出不窮。由復旦大學研究生吳恒創辦的“擲出窗外”網站從各大主流新聞媒體搜集了最近八年以來全國發生的食品安全事件將近3 600條數據記錄，構建成一個相對集中的問題食品資料庫［4］。本次研究利用爬蟲技術，建立數據爬取模型，將網站地址導入模型，隨即獲取網頁信息，讀取每個頁面上的50條事件記錄，直到所有頁面訪問完成。每條記錄包含新聞標題、新聞日期、事件發生地區、事件主題、相關食品、品牌、不安全因素等多個標簽，由于網站中的原始事件列表存在若干無關項或者標簽類別不統一，則需要后續的數據集預處理工作。數據篩選的準則是保留所有有助于挖掘算法實施的記錄，所以需要完成特征選擇與特征工程的相關工作，針對數據記錄中確實存在不統一的屬性標簽或屬性值有所缺失的情況，將數據集的屬性標簽做統一化預處理，將多余屬性排除，將殘缺數據補全。

2.2 食品安全數據的存儲與描述

每一個食品安全事件都是一個數據樣本，這些數據樣本的所有屬性值都是文本型數據，各屬性的取值范圍見表1。

表1 數據對象各屬性取值范圍Tab.1 Value range of each attribute of data object

數據存儲采用電子表格，以CSV純文本形式存取二維數據表。表格中的每一行為食品安全事件記錄，每一列為一種屬性。預處理后得到的食品安全事件數據集格式見表2（因篇幅所限，此處僅提供數據表片段）。

表2 食品安全數據集Tab.2 Food safety data set

3 算法改進與實現

在現實中的分類往往伴隨著模糊性，所以用模糊理論來進行聚類分析也更趨于最優。同時，食品安全數據的最大特點是樣本的每一個屬性經過標準化均取離散型數值，因此該數據模型最適合采用模糊K-Modes算法進行挖掘［5-6］。為了進一步提高算法的有效性，本模型利用加權平均密度的方法自動選取初始聚類中心，并依據信息熵理論重新計算數據集的屬性重要性，以此改進傳統的算法。

3.1 模糊K-Modes算法思想

傳統的模糊K-Modes算法總體思想是對文本型的數據集進行劃分歸類，假設對于一個由n個對象構成的非空集合U＝｛x1，x2，…，xn｝，首先隨機選取k個對象作為k個初始聚類中心，通過0或1匹配的方法計算相異度矩陣，再根據相異度矩陣計算隸屬度矩陣，而后通過隸屬度矩陣將n個對象劃分到最近的初始聚類中心中，形成k個聚類簇，完成一次聚類，計算收斂函數，再通過更新聚類中心的方法在每個聚類簇中重新定義一個新的中心，重復之前的內容計算相異度矩陣、隸屬度矩陣、分配對象，形成k+1個聚類簇，計算收斂函數，比較2次的收斂函數。多次迭代這樣的過程，交替更新聚類中心和隸屬度矩陣，直到式（1）所示收斂函數的值趨于穩定，即聚類中心不再發生偏移，算法結束。

Fuzzy K-Modes算法利用模糊的概念對數據進行軟聚類，大大提高了聚類過程的魯棒性。

3.2 改進的Fuzzy K-Modes算法

信息熵是同一信源發出的各種信息量的平均，可以表征信息環境的無序程度，在一定程度上解決了系統有序度的度量問題［7-8］。根據信息熵理論來計算每個聚類對象的屬性對于分類的貢獻度，可以排除無用屬性。基于傳統的算法思想以及信息熵理論，改進的K-Modes算法具體流程如下:

（1）輸入目標的初始聚類中心數k，k≥1；

（2）根據公式（2）計算屬性總集合A的信息熵E（A）:

E（A）表示整體的信息熵，即所有的屬性將數據集U劃分的情況。其中，A將數據集U劃分成了一個新的集合C，C＝｛A1，A2，A3，……，Ap｝，對于C中的任意一個元素Ai表示數據集U中與Bi的屬性值完全相等的數據集子集，所以Ai?U，且｜A1｜+｜A2｜+｜A3｜+……+｜Ap｜＝｜U｜，｜Ai｜／｜U｜即表示屬性值與Ai完全相等的元素在數據集U中出現的概率；

（3）計算屬性總集合中缺少每個屬性后的信息熵E（A-｛a｝），其中E（A-｛a｝）表示去掉a屬性后，剩余的屬性對U的劃分情況，計算公式與E（A）相同；

（4）根據步驟（2）和步驟（3）獲取的結果，計算每個屬性的權值Sig（a），式（3）:

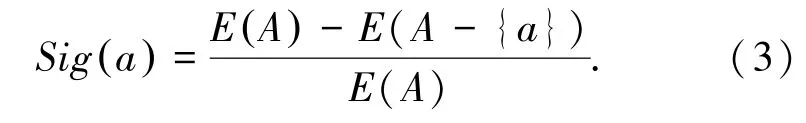
若屬性a對數據集U毫無影響則E（A）＝E（A-｛a｝），說明a對數據集U的劃分沒有起到作用，即Sig（a）＝0，說明a的屬性重要性為0；反之若屬性a對數據集U影響越大，則排除a屬性的E（A-｛a｝）與E（A）就相差越大；

（5）遍歷數據集U，計算每個屬性的平均密度，平均密度的計算公式（4）為:

其中，Densa（x）表示對于A中的任意元素a，對象x在屬性a上的平均密度計算方法為式（5）:

該公式為了計算得出數據集U中與對象x的屬性a的屬性值相同的對象的總數；

（6）對于數據集U中的每一個對象x，計算其加權密度WDens（x），式（6）:

（7）選取所有對象中加權密度WDens（x）最大的一個，將其設為第一個初始聚類中心，加入聚類中心集合Z；

（8）遍歷數據集U中已經選取為聚類中心以外的每個對象x，保存對象的加權密度WDens（x），計算公式與步驟（6）所述相同；

（9）采用0-1相異度度量方法計算對象x與每個已分配好的初始聚類中心的距離之和d（x），式（7）和式（8）:

其中，xi，al，xj，al分別表示數據集中xi和xj2個對象在對應屬性上的屬性值，如果相等則當前屬性間的距離賦值為0，如果不相等則賦值為1，累加所有屬性的屬性間距離，最后得出2個對象之間的距離，即差異度；

（10）對每一個對象x，計算m（x），式（9）:

（11）比較所有的m（x），選取m（x）最大的那個對象作為新的初始聚類中心，加入聚類中心集合Z。

（12）判斷聚類中心數是否達到k個，即｜Z｜＞k是否成立，如果成立跳轉到步驟（13），如果不成立則跳轉到步驟（8），繼續選擇其它的初始聚類中心；

（13）根據步驟（4）所述的Sig（a），計算每個屬性的權值weight（a），式（10）:

（14）用改進的相異度度量方法計算相異度矩陣，式（11）:

其中，δa（xi，xj）參見步驟（9）所述的定義。該公式的含義為任意2個對象之間的距離，當屬性值相同時依然為0，當屬性值不同時取屬性的權值作為距離計算，這樣價值高的屬性影響力就更大。

（15）計算隸屬度矩陣Wl×n，式（12）:

其中，k表示當前數據集劃分為k個簇，即存在k個聚類中心；Zl表示當前第i個類的聚類中心；Zh表示其它類的聚類中心；

（16）根據隸屬度更新聚類中心集合Z，采用屬性眾數作為聚類中心的新的屬性值。即遍歷每一個類簇，計算類簇里每一個屬性的每一個屬性值的總數，用總數最高的屬性值替換當前該類簇的聚類中心；

（17）回到步驟（15）重新計算隸屬度，根據每個樣本的最大隸屬度重新歸類；如果隸屬度不再變化，那么k類的聚類已經完成，跳轉至步驟（18）；

（18）根據當前隸屬度矩陣與相異度矩陣計算聚類準則函數，式（13）:

其中，n是數據集的規模，即聚類對象的數量；Zl＝［zl1，zl2，...，zlm］是能夠代表聚類l的向量，即聚類中心；wi，l∈[0，1]是隸屬度矩陣Wl×n的一個元素，表示對象Xi劃分到聚類l中的隸屬度；∑k l＝1~ωli＝1；wd是改進后的相異度（距離）；α＞1是加權指數；

（19）聚類數量k遞增1，并回到步驟（1），直到k＝n為止，聚類準則函數最小的那一輪聚類為最后的聚類結果。

4 實驗結果分析

為了驗證算法的有效性，利用著名的算法有效性指標正確率AC（accuracy）、類精度PC（precision）、召回率RE（recall）進行實驗比對，式（14）～式（16）:

其中，k表示數據集當前的聚類數量，｜U｜表示整個數據集的對象數量，令ai代表被正確分配到第i類的對象數量，令bi代表被錯誤分配到第i類的對象數量，令ci代表被錯誤排除出第i類的對象數量。實驗中，除了準備好有效性指標之外，還需要有明確分類結果的測試數據集，因此模型中選擇加州大學歐文分校提出的用于機器學習的數據庫——UCI數據庫作為實驗數據，其包含335個數據集，是一個常用的標準測試數據集。該數據集中分別含有數值型數據集與文本型數據集，其中的文本型數據集適用于本模型提出的算法有效性實驗。每個數據集提供了一份完整的數據記錄、分類屬性和分類結果集，實驗中將數據集導入聚類分析模型執行改進的算法，進而計算PC，AC，RE3項指標值，從而檢驗算法的有效性。

本文選擇UCI數據庫中的3個文本型數據集Soybean、Zoo和Vote來檢驗算法。并通過與其它K-Modes算法進行AC，PC，RE指標值的對比，發現本文所改進的算法具有更高的聚類有效性。實驗中選擇隨機選取初始聚類中心的K-Modes算法（Huang’s k-modes with random）和基于平均密度選取初始聚類中心的K-Modes算法（Huang’s k-modes with Xing’s method）參與比較［10］。實驗結果見表3～表5。

表3 Soybean數據集聚類有效性指標表Tab.3 Index table for clustering effectiveness of Soybean data set

表4 Zoo數據集聚類有效性指標表Tab.4 Index table for clustering effectiveness of Zoo data set

表5 Vote數據集聚類有效性指標表Tab.5 Index table for clustering effectiveness of Vote data set

為了更直觀展示3種算法在各實驗數據集上的有效性指標對比，將AC、PC和RE在不同數據集上分別求出平均值生成折線圖如圖1所示。

圖1 聚類有效性指標平均值對比圖Fig.1 Comparison chart of average value of cluster validity index

本次研究中，將改進的聚類算法應用于通過爬蟲系統爬取獲得的食品安全數據集進行規律挖掘，經過對初始數據集的清洗整理，最后篩選出2 751條有效記錄。利用上述算法中對最大聚類數的計算，實驗中需要進行52輪聚類，并分別計算聚類準則函數值，取值最小的那一輪聚類為最后的聚類結果。聚類完成后每個類簇的聚類中心，即每個類中最具有代表性的食品安全事件已經被挖掘出來見表6。需要特別說明的是，由于該數據集網站“擲出窗外”近年來暫無更新，因此安全事件發生日期均是若干年前；同時，被曝光的大多數安全事件中缺乏關于食品品牌的具體數據，因此在預處理數據時均已標記為“未知品牌”。