一種子陣降維帶約束指向的抗干擾方法*

王曉洪，佟 力，毛新勝

（1.成都天奧信息科技有限公司，四川 成都 610041；2.中電科航空電子有限公司，四川 成都 610041）

0 引言

近年來，我國導航產業迅猛發展，為了解決衛星導航信號易受干擾的問題，我國也在大力研究自適應陣列抗干擾[1-6]技術。面臨復雜電磁環境，單純的任意一種抗干擾技術已經顯得能力不足。時域、頻域濾波不能對抗寬帶干擾，空域濾波雖然對寬帶信號具備很好的抑制能力，但由于陣列天線個數有限，能抑制的干擾數目受限；因此，可采用多域聯合處理的抗干擾技術，充分發揮各種方法的優勢，提高設備的抗干擾性能。

目前，一般工程上常采用的是空時聯合抗干擾技術[7-9]，而實現上采用迭代算法（Least Mean Square，LMS），降低其實現難度，但是這樣能達到的效果還是比較有限，并且還犧牲了算法的一部分性能。此外，隨著陣列個數的增加，如相控制陣天線有上千個天線單元，使得即使采用LMS 這樣的迭代算法，也難工程應用，從而空時聯合抗干擾技術在大規模陣列天線上的應用受到限制。隨著相控陣技術的發展，目前對于大規模相控陣天線的抗干擾應用需求也越來越大，而傳統的空時聯合抗干擾算法不能滿足大規模相控陣天線的工程應用 要求。

空時聯合抗干擾技術要求的實時處理能力高，因此一般都是采用現場可編程門陣列（Field Programmable Gate Array，FPGA）這樣的芯片來進行算法的實現，而基于FPGA 芯片的設計中，資源越多算法的反而實時性越好，相反資源越少算法的反而實時性越差；因此，對于空時聯合抗干擾技術來說，尤其是無法實現基于采樣矩陣直接求逆（Sample Matrix Inversion，SMI）[10-12]算法的工程 應用。

本文針對空時聯合抗干擾技術在大規模陣列天線應用上的技術瓶頸，提出一種基于子陣降維帶約束指向的抗干擾方法。該方法在空域進行處理，采用陣元級進行子陣合成，從而實現空間維度進行降維處理的目的，達到減小算法工程應用難度，使得算法基于硬件設計可工程應用，突破SMI 算法在大規模陣列天線上的應用瓶頸，滿足其算法超高精度要求。

1 子陣降維抗干擾技術

子陣降維抗干擾技術，算法分為子陣形成和抗干擾兩個部分。子陣形成可以根據子陣內某一個陣元所在空間位置進行合成形成指向不同方向的子陣，也可以以一個固定空間方向進行合成形成指向同一個方向的子陣。抗干擾采用空時聯合自適應抗干擾方法，具體實現上采用基于采樣數據協方差矩陣求逆的算法。

1.1 子陣內數據的合成

子陣形成是對子陣中各陣元數據的合成，即確定長度為M的合成向量，M為子陣內的陣元個數。無論是根據子陣內某一個陣元所在空間位置還是以一個固定空間方向進行合成，都是利用指向的位置信息(θ,φ)形成合成向量，其中θ為俯仰角，φ為方位角。根據位置信息生成陣元合成的導向矢量，計算公式如下：

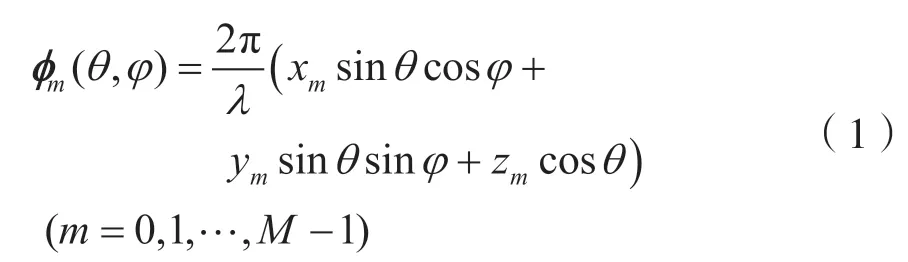
式中：λ代表中心頻點對應的波長；(xm,ym,zm)表示陣元m的坐標值。從而得到M個陣元的合成向 量為：

1.2 空時抗干擾技術

空時陣列處理器結構見圖1，其中T為抽頭間的時間延遲，抗干擾權值為：

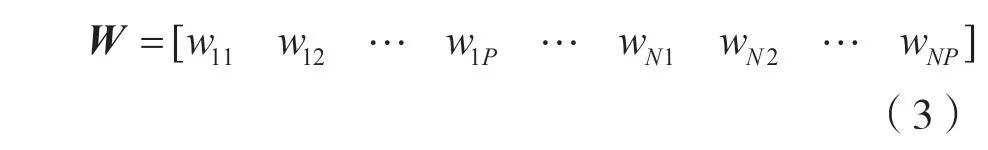
圖1 空時聯合陣列處理結構

抗干擾權值W通過可通過最小噪聲方差準則[13-14]獲得，即使陣列輸出功率最小來選擇最優價權矢量，為避免出現權值為零的情況，需加相應的約束條件。常用的約束方法為保證有用信號無失真通過，也就是陣列對有用信號的響應為常數。因此最小噪聲方差準則的代價函數為：

式中：S(θ,φ)為導向矢量；θ為方位角；φ為俯仰角；R=E{x(n)x(n)H}為子陣接收信號自相關矩陣，這里的x(n)為子陣數據，而傳統方式為陣元數據。對基于SMI 算法，最優解為：

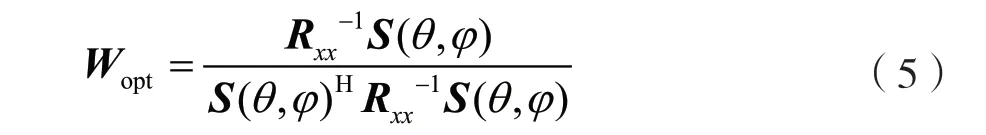
式（5）表示最優波束形成器即為最小方差無失真響應（Minimum Variance Distortionless Response，MVDR）波束形成器。

在監督機制建設中要重點強化企業的成本監督和相關管理工作，要以成本作為監督的目標，理順企業生產、管理的經濟關系，從成本控制的角度構建起有針對性、可執行的監督平臺和監督制度，真正將監督工作的重點放在對企業各項成本的控制工作上，提升企業成本管理、運營管理的效率，打造企業在生產、管理和經營上的經濟、組織與成本優勢。

2 子陣降維多波束算法

數字多波束算法在抗干擾的同時還能對期望方向上的有用信號進行保護，目前工程上常用數字多波束算法停留在陣元級，本文針對子陣級進行數字多波束算法的研究。由前面可知子陣內陣元數據的合成有兩種方式，因此對不同的子陣形成方式就會有不同子陣級數字多波束算法。基于子陣內某一個陣元所在空間位置形成的子陣級數字多波束算法簡稱，后約束子陣級多波束算法。基于以一個固定空間方向進行合成形成指向同一個方向的子陣級數字多波束算法，簡稱為先約束子陣級多波束算法。

2.1 后約束子陣級多波束算法

假設有N個陣元，以任意一個陣元為原點建立坐標系，每個陣元的坐標位置為pm(xm,ym,zm)，m=1,2,…,N。基于子陣內某一個陣元所在空間位置形成子陣，利用子陣內數據合成的方法，共形成M個子陣，每個子陣包含K=N/M個陣元，每個子陣的坐標與合成子陣選擇的參考陣元的位置坐標一致。

采用MVDR 算法，即利用式（5）計算最優權值，首先需要計算基于子陣的期望方向上的導向矢量S(θ,φ)。首先，根據式（1），利用子陣的坐標，即合成子陣選擇的參考陣元的位置坐標，和期望方向的方位θ和俯仰φ得到來波信號的角度值；其次，利用（2）得到導向矢量S(θ,φ)；最后，利用子陣數據得到采樣矩陣Rxx。通過以上方式就完成了后約束子陣級多波束算法。

2.2 先約束子陣級多波束算法

先約束子陣級多波束算法也是根據公式（5）計算權值Wopt。式（5）中設計到子陣之間導向向量S(θ,φ)的計算與后約束的不同，從子陣數據的合成方式可以看出在陣元合成子陣過程中，所有子陣的波束方向都是指向了同一方向，因此式（5）中的S(θ,φ)可簡化為全1 的導向向量，即S(θ,φ)=[1,1,…,1]'，因此不需要再計算子陣之間帶約束的導向向量，算法得到了簡化。根據式（5）計算當S(θ,φ)=[1,1,…,1]'時即為子陣指向目標方向帶約束指向的抗干擾權值。

從上面分析可知先約束子陣級多波束算法較后約束子陣級抗干擾算法的實現方法變得簡單了。主要是省去了MVDR 算法中導向矢量的生成，而且對于全一的導向矢量在計算帶約束抗干擾權值時也變簡單了，省去了式（5）矩陣與導向矢量S(θ,φ)相乘運算中的乘法運算，只有加法運算。

3 算法仿真與分析

3.1 仿真場景

設計3 組實驗考察在低、中、高干擾目標場景下抗干擾性能。各實驗均產生二相相移鍵控（Binary Phase Shift Keying，BPSK）信號作為干擾，載頻1 268 MHz，碼速率10 Mc/s，信息符號隨機生成，陣元個數16 個，陣元間距半波長，根升余弦滾降系數設置為0.35，樣本數取512 個樣本點，繪制方向圖的網格步進為0.1°。實驗中，陣元幅度誤差隨機生成，并服從-0.5～0.5 dB 的均勻分布；陣元相位誤差隨機生成，并服從-5°～5°的均勻分布；其余參數如表1 所示。

表1 實驗參數設置

3.2 干擾抑制和波束保護性能分析

3.2.1 干擾抑制性能分析

分別對基于陣元和子陣級的多波束抗干擾進行仿真對比。由于先約束和后約束從原理上來說是一致的，故仿真的時候就只針對先約束子陣級多波束方法進行仿真。干擾來向（60°,10°），仿真結果見圖2 和圖3；干擾來向（60°,45°），仿真結果見圖4 和圖5；干擾來向（60°,80°），仿真結果見圖6和圖7。

圖2 陣元多波束抗干擾方向

圖3 子陣多波束抗干擾方向

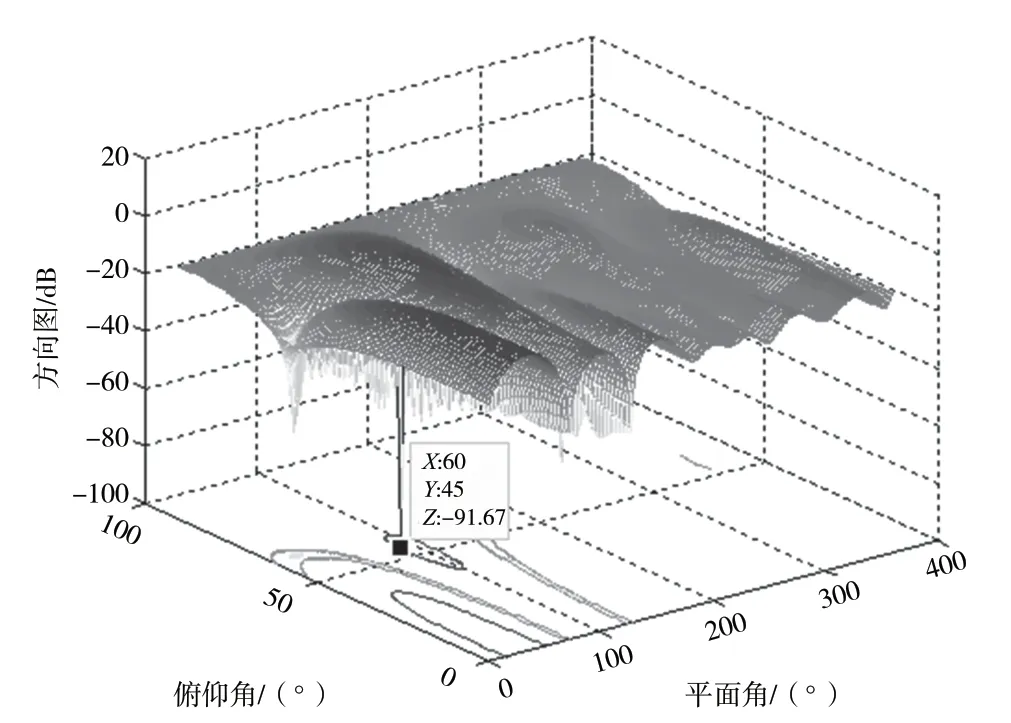
圖4 陣元多波束抗干擾方向

圖5 子陣多波束抗干擾方向

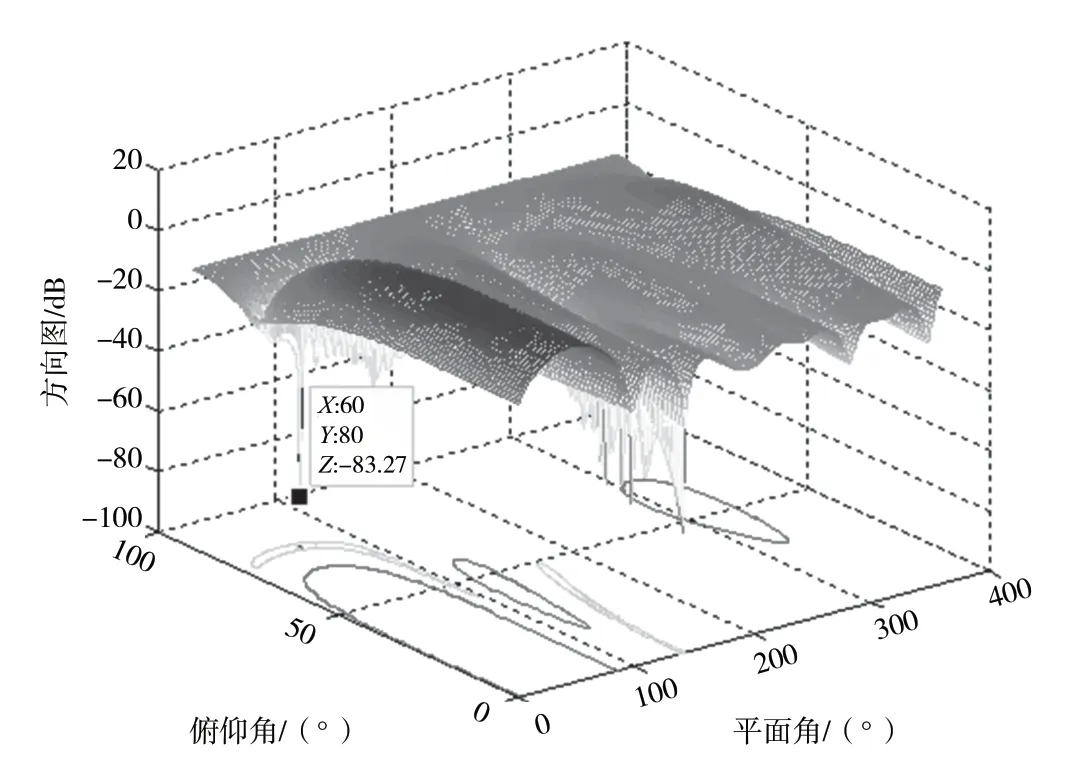
圖7 子陣多波束抗干擾方向

3.2.2 波束保護性能分析

分別對基于陣元和子陣級抗的波束保護性能進行仿真對比。同理子陣級也是只對先約束子陣級多波束方法進行仿真，信號來向（45°,10°）的仿真結果見圖8、圖9 和圖10。

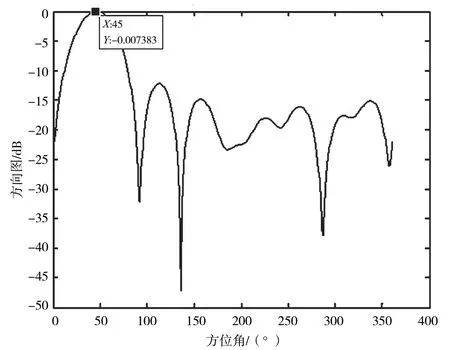
圖8 陣元級二維波束方向

圖9 子陣級二維波束方向圖抗干擾方向

圖10 波束增益對比誤差

從圖8 和圖9 的方向圖可以看出，本文方法在方位45°上形成了有效的波束保護。從圖8 可以看出兩種方式下形成的增益誤差不超過0.45 dB。仿真結果上驗證了基于陣元和子陣級波束保護性能的有效性。

4 結語

由于基于陣列天線的空時聯合抗干擾技術的算法在工程應用中有著較大的實現難度，尤其是對于大型陣列天線，隨著天線個數的增加使得其算法實現成技術瓶頸，限制了其技術的在大型陣列天線如相控陣上的應用。如何降低其實現難度成為技術應用的關鍵，而大部分研究都是圍繞算法實現本身去思考，如LMS 算法。因此需要從最前端進行難度的降低。本文提出了一種子陣降維帶約束的抗干擾算法，此算法是基于MVDR 算法原理的基礎上得到的，并利用陣元級進行子陣合成，從而減少陣元個數，達到保證抗干擾性能的同時又能保證陣列增益。相比陣元級的方案，該方法的所需要的硬件資源有明顯優勢。

基于以上分析可以看出尤其是對于大型陣列天線來說，基于子陣降維帶約束指向抗干擾方法具有明顯的優勢，且可工程化，而傳統陣元級的方式工程化實現難度大，基本不可工程化。仿真結果驗證了算法的抗干擾性能及波束保護性有效性，無論是先約束子陣多波束算法還是后約束子陣多波束算法，相對陣元級的處理其算法的性能并沒有下降，同樣可達到與陣元級算法相同的性能，但是卻降低了算法實現的復雜度；因此，陣列抗干擾技術對于相控陣天線可工程化應用。