基于塊迭代的判決反饋均衡算法研究*

陳安全，楊培消

（海軍士官學校，安徽 蚌埠 233012）

0 引言

短波通信主要利用電離層反射進行數據傳輸，多次反射后傳輸距離可達上萬千米，可實現在全球范圍內的通信[1]。短波通信作為軍事通信的主要傳輸手段之一，具有抗毀性強、機動靈活和網絡重構快捷等一系列優點。隨著通信業務量的不斷增大和種類的不斷增加，人們對短波通信的數據傳輸速率和實時性要求越來越高。然而，短波信道的多徑傳播和時變衰落會造成發送信號畸變和碼間串擾，成為短波數據傳輸的主要制約因素。

短波數據傳輸系統通常采用均衡器來減少碼間串擾，采用信道編碼等技術來對抗干擾和噪聲。均衡器可以看作信道的逆濾波，其傳輸特性與信道特性相反。信號通過均衡器可以補償信道對其造成的失真，同時結合信道編碼提高信息傳輸可靠性，改善系統傳輸性能。傳統接收機將均衡和譯碼看作兩個獨立的功能模塊，兩者共同完成信號的檢測，但從信息處理角度將均衡和譯碼獨立處理會造成信息的損失。因此，從最佳檢測的角度考慮，將均衡和譯碼聯合處理可以獲得更高的性能增益。在接收端對均衡和譯碼進行迭代處理，利用迭代譯碼思想將傳統的檢測估計問題由均衡器擴大到譯碼器，將譯碼輸出的修正的非等概比特信息作為先驗信息反饋給均衡器，然后均衡器利用非等概的先驗似然信息對待檢測的比特或符號重新做出估計。非等概先驗信息的加入，將大大提高均衡效果，從而為譯碼器提供更可靠的譯碼信息。經過若干次聯合均衡和譯碼后，最終將大大提高譯碼輸出的可靠性。塊迭代的判決反饋均衡算法采用聯合均衡與譯碼的迭代處理方式，可以有效對抗短波信道的嚴重碼間串擾。隨著數據傳輸速率的提高，短波通信較大的時延導致時域均衡復雜度大幅增加。基于循環前綴的單載波頻域均衡利用快速傅里葉變換/快速傅里葉逆變換（Fast Fourier Transform/Inverse Fast Fourier Transform，FFT/IFFT）技術將時域復雜的多抽頭濾波卷積轉化成多個單抽頭的頻域相乘，從而降低了均衡技術的計算復雜度[2-4]。為了對抗信道深衰落和線性均衡存在的剩余碼間串擾影響，進一步研究了基于塊迭代的判決反饋均衡（Iterative Block DFE，IB-DFE）算法。

1 塊迭代的判決反饋均衡算法基本原理

基于譯碼先驗信息的判決反饋均衡器，可以利用本次或前次迭代的軟、硬判決值來抵消碼間串擾（Inter-Symbol Interference，ISI）[5-6]。硬判決相比軟判決會造成信息損失，同時硬判決錯誤會從反饋回路傳遞給下一次判決，造成錯誤傳播。與線性均衡不同的是判決反饋均衡屬于非線性均衡，其在線性濾波均衡的基礎上，利用均衡或譯碼器輸出的符號信息來進一步抵消線性均衡存在的剩余ISI。特別是在深衰落信道環境，它可以降低線性均衡器的階數和計算復雜度。早期的IB-DFE 實現考慮的是反饋回路中的硬判決。為了提高性能，文獻[7-8]提出采用軟判決的IB-DFE 方案。IB-DFE 可以視為在頻域上實現的具有前饋和反饋操作的迭代的DFE。由于反饋回路不僅考慮了每個塊的硬判決，而且考慮了所有塊的可靠性，大大減少了傳輸的錯誤。IB-DFE 方案的前饋和反饋部分均在頻域實現。為了對抗短波信道深衰落和線性均衡存在的剩余ISI 影響，重點研究了基于塊迭代的判決反饋均衡 算法。

2 塊迭代的判決反饋均衡算法分析

IB-DFE 數據傳輸系統如圖1 所示。

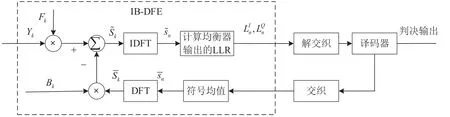
圖1 IB-DFE 數據傳輸系統

經過信道后，接收到的頻域符號可以表示為：

式 中：{Yk;k=0,1,…,N-1} 是{yn;n=0,1,…,N-1}的離散傅里葉變換（Discrete Fourier Transform，DFT）；Yk表示第k個頻點的信道頻率響應；Hk表示相應的信道噪聲。

IB-DFE 輸出的頻域值為：

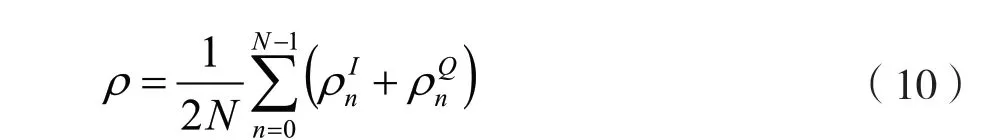
無論是硬判決的IB-DFE 還是軟判決的IBDFE，采用相同的前饋系數。

采用QPSK 的調制方式，均衡器輸出的對數似然比（Log-Likelihood Ratio，LLR）可表示為：

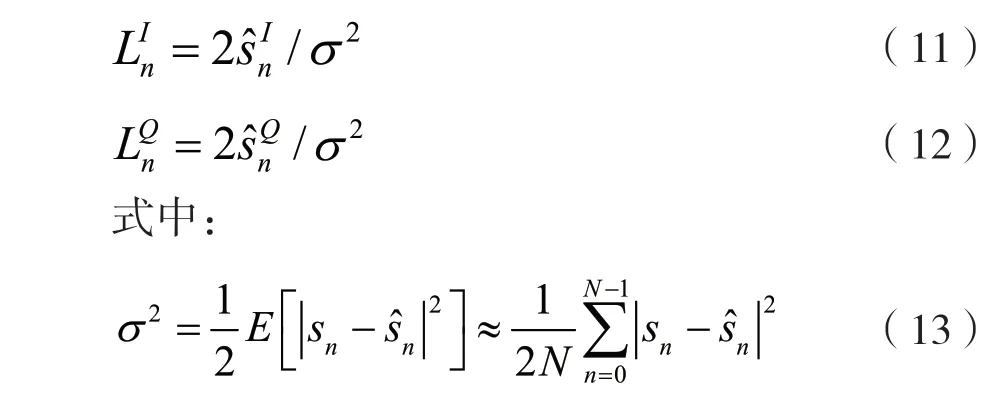
圖2 給出了IB-DFE 算法流程圖。

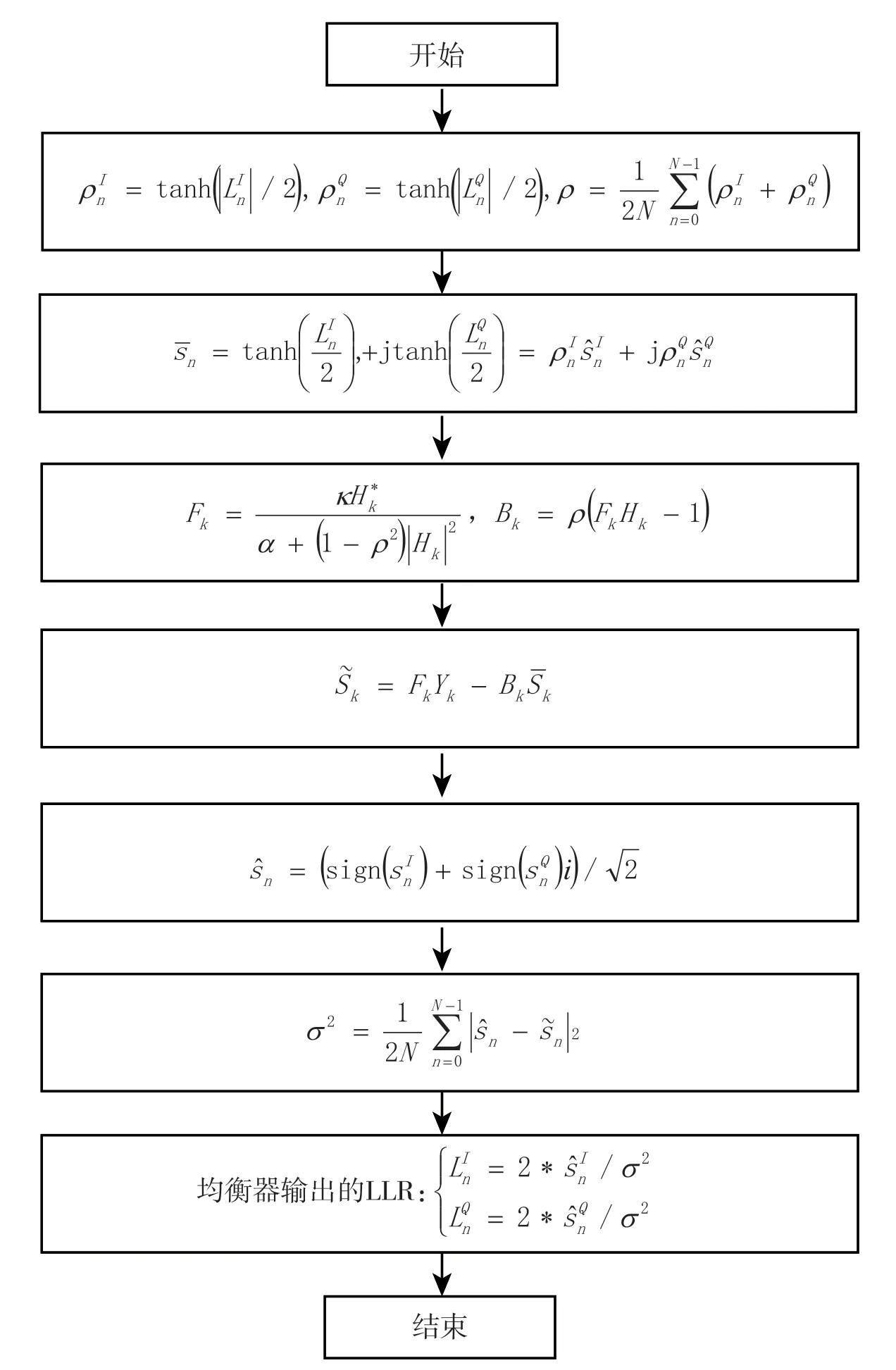
圖2 IB-DFE 算法流程

3 仿真結果及分析

為驗證塊迭代的判決反饋頻域均衡算法的有效性，從塊迭代的判決反饋頻域均衡（IB-DFE）和線性頻域均衡算法在不同迭代次數下的誤比特性能分析。

仿真設置相關參數如下：塊的長度為N=512，采用碼率為1/2，記憶長度為2，生成矩陣為g=[111;101]的卷積碼。此外，采用隨機交織器和QPSK調制方式。信道采用Proakis B 信道h(n)=[0.407 0.815 0.407]，噪聲為高斯白噪聲。譯碼器采用對數域最大后驗概率（Maximum-logarithm-Maximum a Posteriori Probability，MAX-Log-MAP）譯碼算法。假設一個數據塊內信道保持恒定，信道參數為接收端所知。仿真參數設計如表1 所示，仿真結果如圖3 所示。

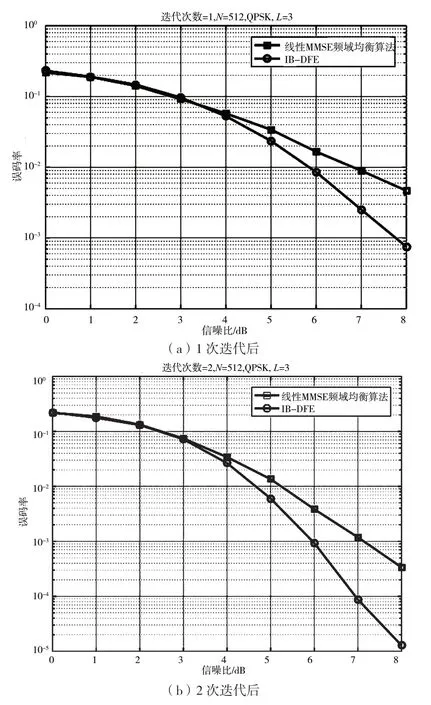
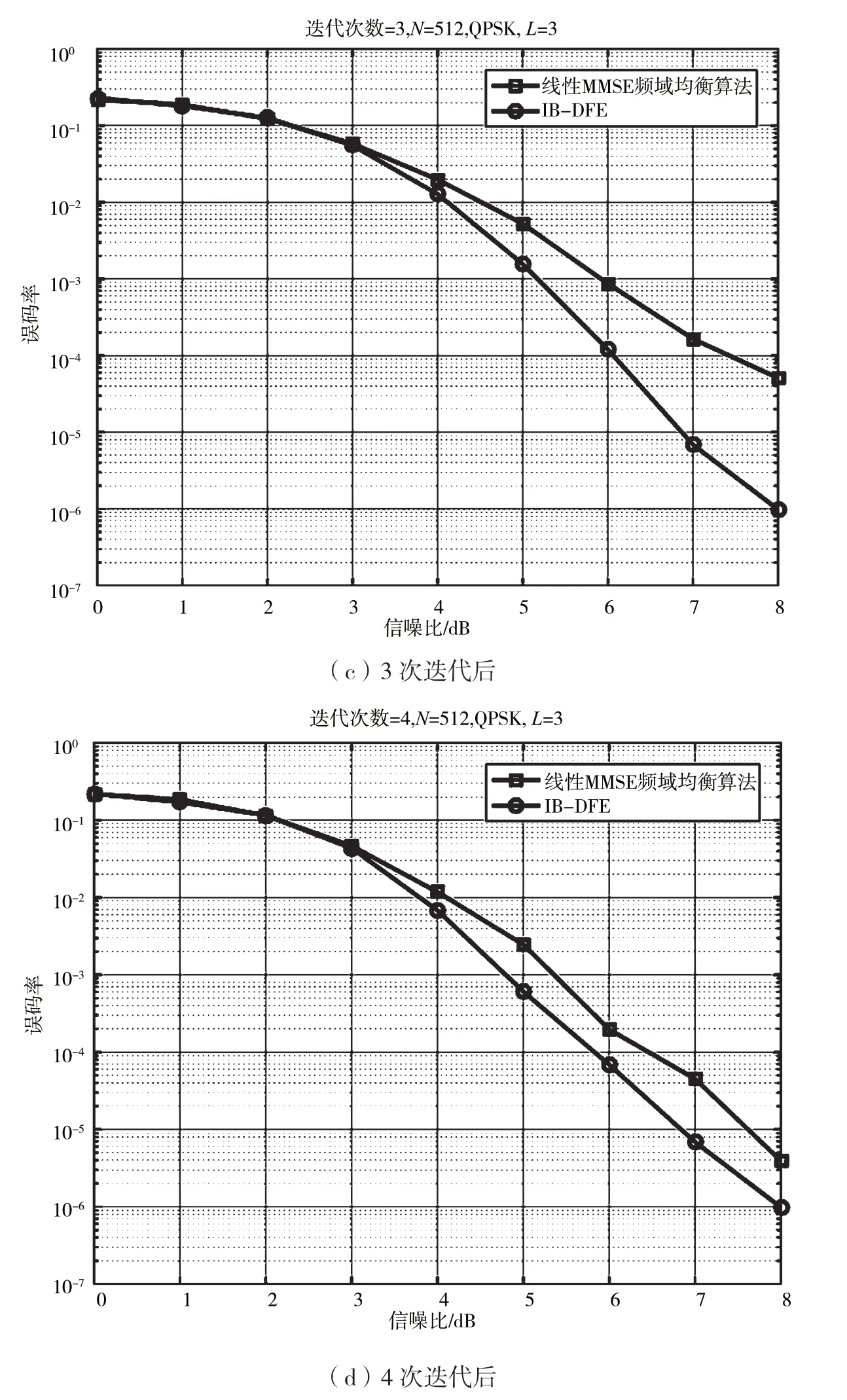
圖3 線性MMSE 頻域均衡算法和IB-DFE 的誤比特率對比

表1 IB-DFE 和線性MMSE 頻域均衡算法對比時的仿真參數

由圖3 可知，在Proakis B 信道條件下，隨著信噪比的增加，IB-DFE 相比線性頻域均衡算法有較大的性能改善。在迭代2 次達到10-3誤碼率時，IB-DFE 相比線性MMSE 頻域均衡算法的誤碼率提升了約1 dB。究其原因，線性均衡只能削弱碼間串擾，不能完全消除碼間串擾。IB-DFE 均衡前饋濾波器和反饋濾波器的結合使用能抵消前向和后向的ISI。因此，與線性頻域均衡相比，IB-DFE 具有較好的誤比特性能。

4 結語

本文介紹了短波通信的重要意義和短波信道的多徑傳播會造成發送信號的碼間串擾。為消除碼間串擾的影響，圍繞塊迭代的判決反饋頻域均衡算法進行研究，對塊迭代的判決反饋頻域均衡算法進行理論推導并進行仿真實驗。通過對比線性頻域均衡和IB-DFE 算法可知，在典型的短波多徑信道條件下，塊迭代的判決反饋均衡（IB-DFE）算法具有較好的誤比特性能。