自重荷載下非均勻支撐板式無砟軌道靜態響應

蔣紅光 劉舜 李宜欣 李昕亮 薛志超 姚占勇

摘? ?要：針對高速鐵路路基不均勻沉降誘發的板式無砟軌道幾何形態和應力狀態惡化問題，建立了高速鐵路CRTSII型板式無砟軌道-路基三維有限元模型，模擬了64種路基不均勻沉降組合（波長5～40 m，波幅5～40 mm），提出了基于混凝土底座柔度的形態映射和應力水平定量表征方法. 研究結果表明，軌道結構的形態映射特征主要由混凝土底座柔度決定，在沉降波長小于15 m、或者波長在15～20 m之間且沉降幅值大于15 mm時，軌道結構與路基因變形不協調而出現脫離. 軌道結構變形量的增加會導致混凝土結構附加拉應力和路基接觸應力的增大，且易接近或超過相應的強度允許值而產生損傷破壞. 同時，增加混凝土底座的模量和厚度，對提高軌面幾何平順性的效果并不顯著，反而會增大結構自身的拉應力和路基接觸應力.

關鍵詞：高速鐵路;路基不均勻沉降;柔度;幾何形態;附加應力

中圖分類號：U213.2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

Static Responses of Unevenly Supported

Ballastless Track under Self-weight Loads

JIANG Hongguang1，LIU Shun1，LI Yixin1，LI Xinliang1，XUE Zhichao2，YAO Zhanyong1

（1. School of Qilu Transportation，Shandong University，Jinan 250002，China;

2. Shandong Hi-speed Group Engineering Detection Co Ltd，Jinan 250098，China）

Abstract：To evaluate the deterioration problem of geometry and stress states for the ballastless track caused by the uneven subgrade settlement of high-speed railway，a 3D FEM model of the CRTS ΙΙ type ballastless track-subgrade system was established in this paper. A total of 64 types of differential settlements were simulated （with wavelengths of 5～40 m and amplitudes of 5～40 mm）. Based on the flexibility of the concrete base，quantitatively characterizing method for the geometry mapping and stress level of the track structure was proposed. The results show that the mapping characteristics of the track structure are mainly determined by the flexibility of the concrete base. When the settlement wavelength is less than 15 m or the wavelength is between 15～20 m with the settlement amplitude greater than 15 mm，the subgrade and track are separated due to uncoordinated deformation. The increase of the track structure deformation leads to the development of additional tension stresses in the concrete structure and the subgrade contact stresses，which are prone to approach or exceed their allowable strength and results in damaged failure. Meanwhile，an increase of the modulus and thickness of the concrete base is not significant for improving the smoothness of the rail surface. On the contrary，it increases the track tensile stress and the subgrade contact stress.

Key words：high-speed railway;subgrade differential settlement;flexibility;geometry;additional stress

經過10多年的快速發展，我國已成為世界上高速鐵路規模最大、運營速度最高的國家. 列車的高速運行對軌道的平順性提出了非常嚴格的要求，而路基作為軌道的重要支撐結構，需要為軌道提供平順的幾何形狀. 但是在實際工程中，路基往往會產生不均勻沉降[1-2]，考慮到扣件系統高度的調節極限，我國高鐵設計規范要求普通路基段20 m內的不均勻沉降不得超過15 mm. 在自重荷載作用下，非均勻路基支撐將導致軌道結構附加應力增大，影響交通基礎設施的耐久性. 由于板式無砟軌道的整體剛度非常大，其軌面變形并非與路基不均勻沉降完全一致，軌下結構損傷往往具有很強的隱蔽性，一旦發展到軌道結構應力損壞，維修和更換難度非常大，因此需要充分評估非均勻支撐下的板式無砟軌道幾何形態和力學響應.

對于路基不均勻沉降對上部結構和列車運行的影響，大多以理論研究為主. 鄒春華等[3]采用余弦函數表示路基不均勻沉降，基于連續彈性支承梁理論，得到了有砟軌道軌面沉降分布計算公式. 吳仲倫[4]在研究路基凍脹引起的軌面不平順時，基于有限元模型建立了具有一定初始隆起形狀的路基，進而獲得了軌道結構和鋼軌對應的幾何不平順. Paixao等[5]基于有限元模型，較為系統地研究了路基不均勻沉降波長和幅值對輪軌動力響應的影響，并基于安全性和舒適性要求提出了相應的控制指標. 針對整體剛度更好的板式無砟軌道，陳仁朋等[6]研究了路基中長波不平順下軌道板的受力，并基于抗彎疲勞強度允許值，提出了路基不均勻沉降的控制準則. 由于路基沉降主要來自地基下沉，羅強等[7]研究了地基差異沉降模式、路堤高度等因素對路基面不均勻變形的影響，并建立了兩者的映射關系. 陳兆瑋等[8-9]對不同類型板式無砟軌道系統的鋼軌變形和橋墩沉降映射關系進行了理論推導，并獲得了鋼軌的變形區域與幅值. 蔣麗忠等[10]建立了數值解析模型和有限元模型，研究了不均勻沉降發生在不同路橋位置處的鋼軌變形形態與映射關系. 何春燕等[11]進一步研究了路橋過渡段不均勻沉降與鋼軌變形的映射關系，并應用于列車的動力學分析. 肖威[12]、裴國史[13]等分別針對高速鐵路和有軌電車線路建立了板式無砟軌道數值模型，分析了軌面變形、軌道結構應力與路基不均勻沉降波長和幅值的相關規律. 徐慶元等[14]綜合考慮了軌道不平順、路基不均勻沉降、溫度梯度和列車荷載的影響，基于混凝土底座疲勞破壞限值，提出高速鐵路CRTSⅠ型板式無砟軌道的不均勻沉降限值為7 mm/20 m，但未研究其他沉降波長的影響. 張克平等[15]建立了考慮軌道自重荷載的車輛-軌道動力學模型，分析了行車速度、路基不均勻沉降波長和幅值對車輛動力學性能的影響.

綜上可見，當路基發生不均勻沉降后，軌道結構力學響應不僅受列車動載的影響，也與其自重荷載作用密切相關. 而且，不同路基支撐條件下的軌道結構抗彎剛度也在很大程度上決定了變形和應力的傳遞. 實際上，軌面的形態映射和力學響應是軌道結構參數與路基不均勻沉降型式共同作用的結果，Auersch[16]基于Winkler地基上的單層彈性支承梁模型，指出軌道存在一個與軌道抗彎剛度有關的截止波數，決定了軌面的映射特征. 現有研究大多集中在路基不均勻沉降對軌道結構應力狀態的定性討論，未能建立路基不均勻沉降與軌面變形和軌道結構受力狀態的定量關系. 本文通過建立高速鐵路 CRTSII 型板式無砟軌道-路基三維有限元模型，研究了典型路基不均勻沉降組合下的軌面映射特征，提出了考慮不均勻沉降波長的混凝土底座柔度，建立了基于柔度表征的軌面-路基幾何形態映射、附加應力以及路基接觸應力的相關關系，以定量評估非均勻支撐板式無砟軌道靜力響應，提出敏感的不均勻沉降型式，并討論了改變混凝土底座模量和厚度對提高軌面幾何平順性的效果.

1? ?數值模型

1.1? ?板式無砟軌道三維有限元模型

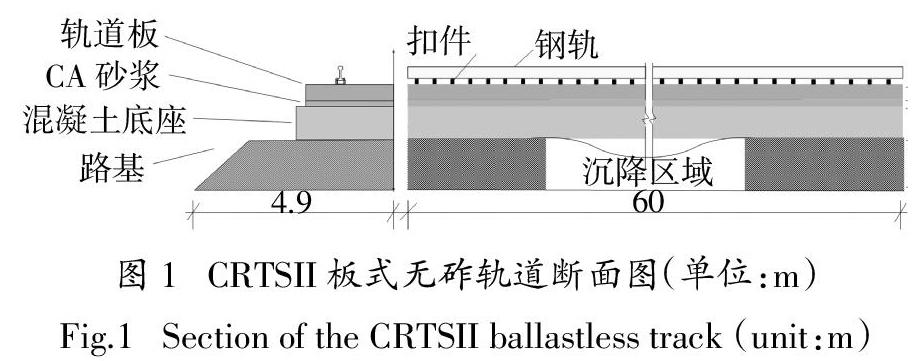
根據中國高速鐵路廣泛使用的CRTSII型板式無砟軌道，建立了三維有限元模型如圖1所示. 其中，模型總長60 m;鋼軌采用UIC60型，以連續的歐拉梁單元模擬;軌道板2.6 m（寬）×0.2 m（厚），CA砂漿層（CAM）2.6 m（寬）×0.05 m（厚），混凝土底座3.25 m（寬）×0.3 m（厚），基層表層0.4 m厚，采用六面體實體單元模擬. 鋼軌采用WJ-7型扣件系統固定到軌道板上，以剛度為28.5 kN/mm的垂直彈簧單元模擬. 考慮到不均勻沉降的存在，當垂直接觸壓力降為零時，路基、混凝土底座、CAM層和軌道板之間的界面允許分離. 法向采用硬接觸，切向接觸由庫侖摩擦模型模擬，接觸面在開始相對滑動之前可承受臨界切應力. 模型底部為固定邊界，四周采用對稱約束并允許產生豎向位移U2. 數值模擬的計算參數根據浙江大學物理模型試驗取值[17]，見表1.

1.2? ?數值模型可靠性驗證

浙江大學建立了全比尺的板式無砟軌道物理模型試驗裝置，并開展了列車輪軸作用下的扣件荷載分擔比試驗[18-19]. 作動器通過分配梁將荷載傳遞至兩側鋼軌上，例如當分配梁分別置于5#扣件和4#與5#扣件之間時（見圖2），模擬了列車輪軸分別移動至扣件上方和相鄰兩個扣件之間. 作動器分級施加荷載50～200 kN，增量為50 kN. 千分表固定在軌道板表面，以記錄各級荷載下扣件系統的壓縮變形，通過扣件剛度可換算得到分擔到的荷載值. 圖2給出了各個扣件在分級載荷下的實測變形. 當軸向載荷直接施加在扣件上方時，約5對扣件分配軸載. 軸向載荷從50 kN增加到200 kN時，扣件的最大變形從0.3 mm增加到1.2 mm. 當軸載作用在兩個相鄰扣件之間時，大約6對扣件分配軸載，鋼軌最大變形量也從0.3 mm增加到1.2 mm. 數值模擬結果如圖2中實線所示，在兩個不同的位置施加軸載時，均與物理模型試驗結果吻合較好. 因此，后文將采用該三維有限元模型進一步研究路基不均勻沉降作用下板式無砟軌道結構的形態映射和附加應力特征.

1.3? ?不均勻沉降模型

有限元模型中，路基不均勻沉降的波長和幅值特征采用余弦函數表示，見式（1）.

式中：s（x）是路基沉降;A0和L0分別是沉降幅值和波長;x0是路基沉降發生的初始位置. 數值模擬中選取不均勻沉降的波長為5～40 m，間隔5 m;沉降幅值為5～40 mm，間隔5 mm，共計64種組合. 在對路基施加不均勻沉降之前，首先對模型進行地應力平衡，使其初始變形為零. 隨后，路基頂部節點向下移動以生成不均勻沉降邊界，如圖1所示.

2? ?軌道結構幾何映射特征

圖3給出了路基不均勻沉降15 mm（波幅）/ 10 m （波長）時軌道各層結構的變形. 在自重荷載作用下，軌道結構同樣產生波長為10 m的不均勻下沉，表明路基的沉降波長將完全映射至軌道. 但是，從沉降幅值來看，軌道結構由于自身剛度較大，并未跟隨路基一并下沉，而且鋼軌與各層軌道結構的變形協調一致. 例如當路基不均勻沉降幅值為15 mm時，軌道結構的沉降幅值僅為5.63 mm，此時軌道結構與路基產生脫離，將會導致軌道結構內應力增加，而且降水容易匯集此處，加劇路基和混凝土結構的水損害. 另外，軌道結構較高的剛度導致在沉降區域的兩側出現了0.35 mm的上拱，這也將加劇列車的輪軌相互作用.

由于路基不均勻沉降的波長特征完全映射至鋼軌表面，現僅給出64種路基不均勻沉降組合下鋼軌的位移幅值，如圖4所示，可分為3個典型的波長范圍. 當沉降波長小于10 m時，沉降幅值對軌道結構的位移映射幾乎沒有影響. 換言之，盡管在軌道表面測得的沉降相對較小，但并不表示路基沉降也很小. 該階段的軌道脫空若能及時發現并得到注漿修復，并不會影響軌道結構的幾何形態. 當沉降波長發展至超過20 m時，路基沉降量無論多大，軌道結構的位移與路基沉降一致，軌道結構與路基始終保持接觸，此時恢復軌道的幾何形態將非常困難. 當沉降波長為16 m且沉降波幅小于15 mm時，軌道結構隨著路基一同沉降，之后隨著沉降幅值的增加，軌道結構與路基發生脫離，其位移幅值要低于真實的路基沉降幅值.

一旦路基發生不均勻沉降且混凝土底座與路基之間產生脫空后，脫空區將喪失支撐作用. 從圖3看，整個軌道結構作為一個整體同步產生彎曲，跨距近似等于沉降波長，則板中心最大變形可表示為：

式中：q為施加在板表面的均布荷載;L0是跨距，即沉降波長;Dc是板的截面彎曲剛度;α是系數;E和h分別是彈性模量和板厚度;μ是泊松比. 對于同樣的不均勻沉降跨距，軌道各層結構的變形主要由其彎曲剛度決定，根據表1可得到鋼軌、軌道板、CA砂漿層和混凝土底座的彎曲剛度分別為：6.42×106 N·m、2.40×107 N·m、7.99×102 N·m和5.55×107 N·m. 可見，混凝土底座的彎曲剛度最大，相應的變形量最小. 由于路基不均勻沉降首先映射至混凝土底座，混凝土底座的變形將決定整個軌道結構其他部分的幾何形態. 這也與上文描述一致，即軌道各層結構的位移保持一致. 因此，可根據式（2）（3）計算得到混凝土底座變形量，即為軌道結構的整體位移量. 對于給定自重荷載下的軌道結構，變形量Δmax由L40和Dc決定. 將混凝土底座的柔度δ定義為：

其中，q0 = 1 kPa，沉降波長越長，相應的柔度和變形量將越大. 圖5給出了混凝土底座不同厚度和模量變化下柔度與不均勻沉降波長的關系，混凝土底座厚度和模量分別取值20～40 cm和24～35 GPa. 其中，現行高速鐵路設計規范建議采用的混凝土底座厚度和模量為40 cm和24 GPa. 結果表明，混凝土底座柔度隨波長呈指數式增長. 當波長小于15 m時，柔度幾乎不受沉降波長甚至是厚度和模量的影響;當波長超過20 m時，柔度快速增長，并處于較高水平;波長15～20 m是柔度變化的過渡區. 柔度隨沉降波長的發展規律與圖4中的軌道位移映射規律一致，這也證實了軌道結構和路基之間的映射特性主要由混凝土底座柔度決定. 若能控制路基不均勻沉降波長不超過15 m，將很大程度上降低混凝土底座柔度和軌面變形.

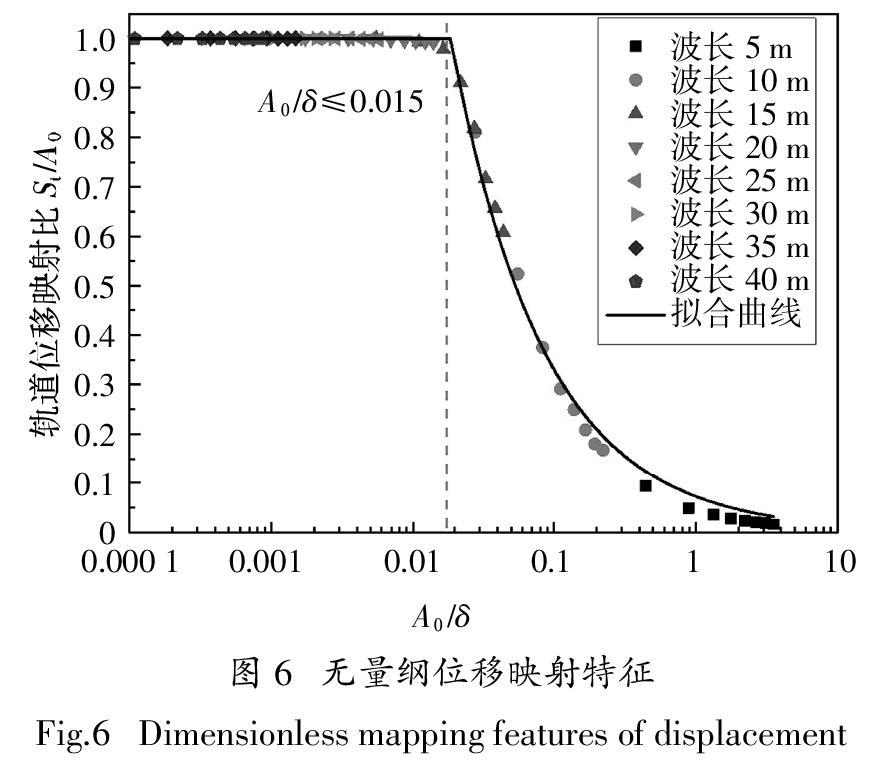
圖6給出了不同沉降組合下的無量綱映射關系，其中縱坐標為軌道位移映射比，定義為軌道位移幅值St與路基沉降幅值A0的比值，St /A0=1.0表示路基沉降完全映射至軌道表面;St /A0<1.0表示軌道結構與路基出現脫空. 橫坐標是沉降幅值A0與柔度δ的比值，綜合考慮沉降幅值、波長和軌道參數的影響，可以發現，軌道位移映射比與歸一化的沉降幅值A0 /δ具有很好的相關關系，可通過分段函數表示：

從圖6可發現，存在臨界值A0 /δ = 0.015，用來判斷軌道結構是否與路基分離. 對于A0 /δ ≤0.015的情況，位移映射比始終為1.0，對應于沉降波長大于20 m或是波長為15 m且幅值小于15 mm的情況，此時路基的沉降完全映射到軌道結構，在軌道表面測得的沉降量即為路基的沉降. 當歸一化沉降幅度A0 /δ > 0.015時，對應沉降波長小于15 m，此時的柔度很小，如圖5所示，位移映射比隨著歸一化沉降幅度的增加而迅速減小. 對于沉降波長為15 m、10 m和5 m的情況，隨著沉降幅值從5 mm增加到40 mm，軌道位移映射比分別為1.0～0.61、0.52～0.17和0.09～0.02，這意味著此時從軌道檢測獲得的沉降將低于實際路基沉降量，在波長小于10 m時尤其明顯.

3? ?附加應力

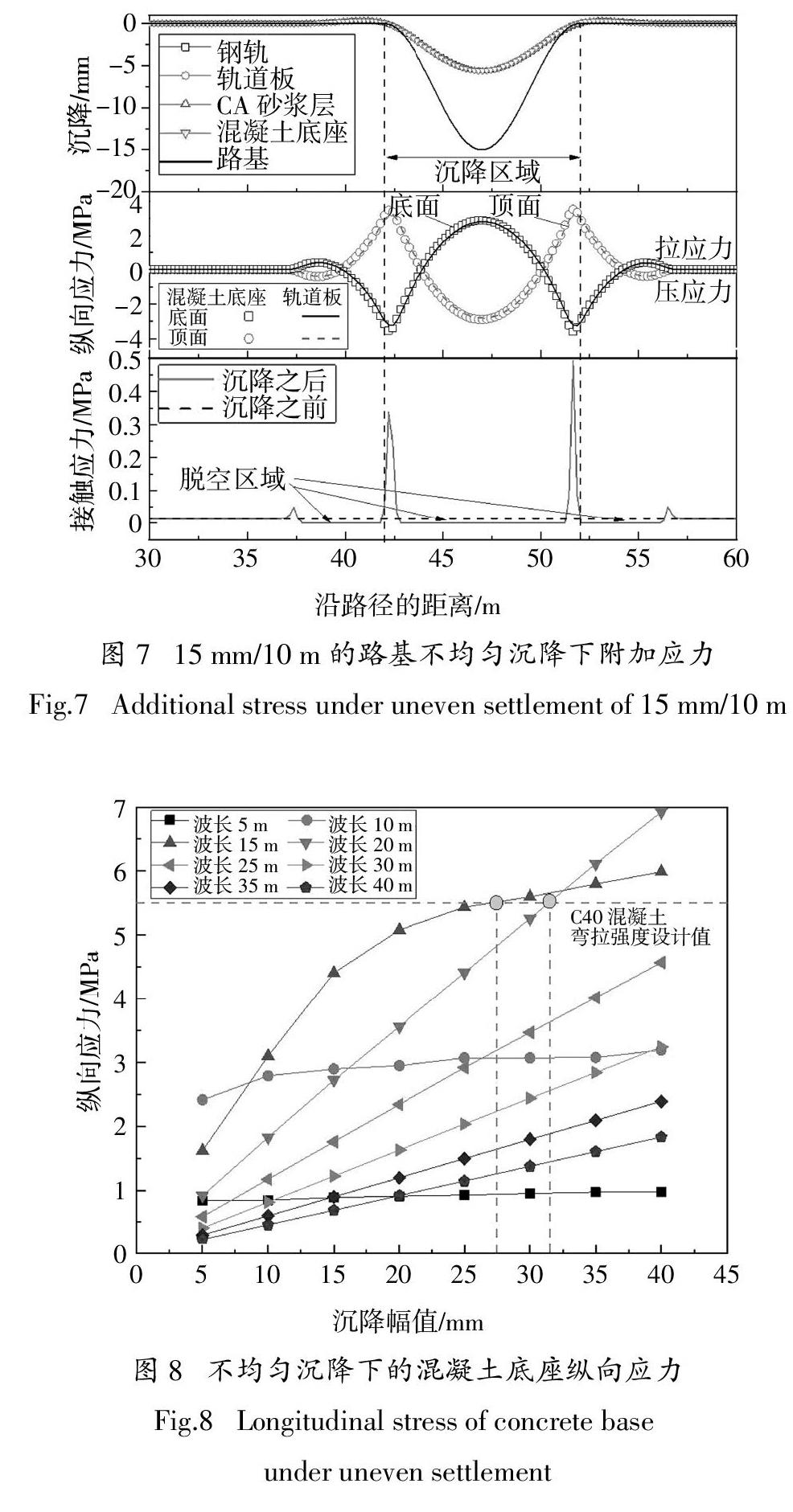
運營初期的高速鐵路路基不均勻沉降量較小，在列車行駛的間隔期，軌道結構和路基僅承受其自重荷載，軌道結構幾乎不存在附加的縱向應力（溫度應力除外）. 一旦路基產生不均勻沉降，隨著軌道變形量的增加，相應的附加應力也逐步增大，尤其是軌道結構和路基脫空后. 以15 mm（波幅）/10 m（波長）為例，路基不均勻沉降引起的軌道板和混凝土底座縱向附加應力、路基接觸應力分布如圖7所示. 可見，軌道板和混凝土底座的底面和頂面均存在較大的拉應力區域，其中，板底的最大拉應力出現在不均勻沉降的中心區域，而板頂的最大拉應力出現在不均勻沉降引起的拱起區域. 因此，在軌道結構強度設計時，軌道板和混凝土底座表面的抗彎拉能力同樣值得重視. 另外，路基不均勻沉降發生后，脫空區域的接觸應力降為零，由于接觸面積的減小，沉降區域的邊緣將產生應力集中，例如沉降發生前路基表面的初始靜應力為0.014 MPa，沉降發生后增大至0.5 MPa，這將加速路基土體的性能弱化.

不同沉降幅值和波長組合下的混凝土底座縱向應力如圖8所示. 當不均勻沉降波長低于15 m時，混凝土底座的縱向拉應力隨著波長的增加而增大. 其中，沉降波長為5～10 m時，混凝土底座的縱向拉應力基本不隨沉降幅值的增加而增大，分別為0.9 MPa和3.1 MPa;沉降波長為15 m時，混凝土底座的縱向拉應力隨沉降幅值的增加由1.6 MPa逐漸增大至6.0 MPa;當沉降波長為20～40 m時，混凝土底座的縱向拉應力同樣隨沉降幅值的增加而線性增大，隨波長的增大而逐漸減小，最大值由6.9 MPa（波長20 m）減小至1.8 MPa（波長40 m）. 若以C40混凝土彎拉強度設計值5.5 MPa為控制標準，在天窗期間僅考慮軌道結構自重作用下，不均勻沉降幅值和在對應的波長下應不超過27.5 mm（波長15 m）和31.5 mm（波長20 m）.

圖9給出了混凝土縱向應力與歸一化沉降幅值A0 /δ的相關關系，其中縱坐標是縱向應力σwc與沉降波長L0的比值. 對于波長大于15 m的情況，混凝土底座與路基保持良好接觸，縱向應力σwc近似表示為：

實際上，若考慮列車荷載的疲勞效應，不均勻沉降控制標準將更為嚴苛. 根據混凝土疲勞強度史密斯設計理論，混凝土疲勞強度不僅取決于循環中的最大應力，而且取決于最小應力，如圖10（a）所示. 其中βBZ為混凝土的彎曲抗拉強度，對于C40混凝土底座，βBZ = 5.5 MPa;σwc為最小拉應力值，即自重荷載作用下的附加應力;n為列車荷載循環次數，對于板式無砟軌道，一般考慮200萬次荷載循環，即n=2×106;σQ為疲勞強度允許值，即列車荷載引起的混凝土底座拉應力σD應低于σQ. 混凝土的彎曲疲勞強度允許值σQ與附加應力σwc關系為：

混凝土底座疲勞強度允許值與不均勻沉降幅值和波長的關系如圖10（b）所示. 可見，隨著混凝土底座附加應力的增加，疲勞強度允許值逐漸減小. 其中，當不均勻沉降波長為15 m和20 m、相應的沉降幅值分別超過15 mm和20 mm時，由不均勻沉降導致的混凝土底座附加應力已達到彎曲疲勞強度允許值σQ. 對于其他沉降工況，需要進一步結合列車動荷載導致的混凝土拉應力，以判斷混凝土底座的疲勞開裂情況.

不同沉降組合下的路基表面接觸應力峰值如圖11所示. 波長為5 m和10 m時，接觸應力穩定在0.25 MPa和0.53 MPa. 而波長為15 m時，接觸應力在沉降幅值較小時處于低應力水平，此時并未發生脫空;而后隨著沉降幅值快速增加至0.65 MPa，超過了路基允許壓應力0.15 MPa的參考值[12].當沉降波長達到20 m及以上時，路基接觸應力快速減小，處于較低的應力水平. 可見，路基接觸應力的不利波長范圍為10～15 m，且隨沉降范圍和幅值的增加而增大，主要集中在脫空情況下發生. 列車荷載作用下，路基通常先產生波長和幅值較小的局部沉降，此時將導致接觸應力重分布，使得沉降區域邊緣的應力水平增加，導致土體逐漸進入屈服階段，進而產生更大的沉降變形和更廣的沉降區域. 應該注意的是，在沉降波長處于10～15 m范圍內，沉降幅值和沉降范圍的增長存在著惡性循環關系. 因此，應及時對波長小于10 m的局部沉降進行修復，以避免沉降區域的進一步發展和對軌道結構的潛在威脅. 圖12進一步給出了路基接觸應力σcs與歸一化沉降幅值A0 /δ相關關系，并近似表示為：

4? ?軌道結構模量與厚度的影響分析

軌道結構幾何形態映射和附加應力主要與混凝土底座的柔度有關，依次選取混凝土底座模量24 GPa、30 GPa和35 GPa，厚度20 cm、25 cm、30 cm、35 cm和40 cm，分析其對板式無砟軌道靜力學性能的影響. 計算時選取路基不均勻沉降波長為20 m、幅值為15 mm.

圖13給出了混凝土底座模量對各結構層變形和受力特性的影響. 軌道結構最大變形和附加應力最大值所對應的位置均處于最大沉降處上方. 從圖中可以看出，當模量從24 GPa增加到35 GPa時，路基不均勻沉降導致的軌道結構各層最大變形和混凝土底座拉應變略微減小，分別降低了約0.2%和1.9%;軌道板、CA砂漿與混凝土底座的層間接觸應力分別降低了5.3%、4.8%，而路基表面的接觸應力發生了較為明顯的增長，由0.17 MPa增加至0.22 MPa，增幅24.1%，表明路基接觸應力對軌道剛度的變化更為敏感. 增大混凝土模量對于提高軌道結構抵抗變形能力的作用并不顯著，反而增加了路基接觸應力.

圖14進一步給出了路基不均勻沉降作用下混凝土底座厚度變化對各結構層變形和應力的影響. 從圖14可看出，當混凝土底座厚度從20 cm增加到40 cm時，路基不均勻沉降導致的軌道結構各層最大變形略微減小，軌道板與CA砂漿、CA砂漿與混凝土底座的接觸應力分別降低了27.9%、29.0%;而混凝土底座拉應變和路基表面的接觸應力發生了較為明顯的增長，分別提高了2.9倍和1.9倍. 可見，增大混凝土底座的厚度雖然提高了軌道的抗變形能力，但由于其自重的增加，反而導致混凝土底座拉應變和路基接觸應力增幅顯著. 因此，在通過增大軌道結構抗彎剛度提高軌面幾何平順性時，也要考慮到其對結構自身拉應變和路基接觸應力的不利影響.

5? ?結? ?論

1）軌道各層結構始終保持接觸，其變形波長特征與路基不均勻沉降幾乎一致，但在沉降區域的兩側出現略微的拱起;軌道結構與路基的接觸狀態受不均勻沉降波長和幅值的共同影響，在沉降波長小于15 m，或者波長在15～20 m之間且沉降幅值大于15 mm時，軌道結構與路基出現脫空，此時通過軌道結構測試得到的沉降會低估路基的實際沉降量.

2）軌道結構變形量的增加會導致混凝土結構附加拉應力和路基接觸應力的增大，尤其是軌道結構和路基脫空后，附加應力也會隨著沉降范圍的擴大而增大. 其中，混凝土底座的附加應力最接近于其疲勞強度，易發生開裂破壞;路基接觸應力過大也容易導致土體產生塑性屈服，擴大不均勻沉降的幅值和范圍.

3）軌道結構的映射特性主要由混凝土底座柔度決定. 波長小于15 m時，柔度很小，幾乎不受沉降波長甚至是厚度和模量的影響，此時的軌道幾何形態映射量很小但附加應力較高;當波長超過20 m時，柔度快速發展，軌道變形量較大但附加應力較低;同時，軌道結構形態特征和附加應力與沉降幅值和柔度的比值A0 /δ有很好的相關關系，并分別建立了軌道結構變形量、混凝土結構附加應力以及路基接觸應力與A0 /δ的經驗計算公式.

4）在現有的設計參數范圍內，增加混凝土底座的模量和厚度對提高軌面幾何平順性并不顯著，反而會增大結構自身的拉應力和路基接觸應力.

下一步將考慮引入車輛荷載，研究軌道幾何形態映射對列車高速運行的影響.

參考文獻

[1]? ? 蔣正舜，茍志龍. 內馬鐵路陡坡路基不均勻沉降及影響因素分析[J]. 湖南大學學報（自然科學版），2018，45（S1）：25—29.

JIANG Z S，GOU Z L. Analysis of uneven settlement and influencing factors of steep slope at Nairobi-Malabar railway[J]. Journal of Hunan University （Natural Sciences），2018，45（S1）：25—29. （In Chinese）

[2]? ? 陳仁朋，朱建宇，姜正暉，等. 基于舒適性的軟土地區公路行駛質量評價方法[J]. 湖南大學學報（自然科學版），2020，47（7）：120—127.

CHEN R P，ZHU J Y，JIANG Z H，et al. Evaluation method of driving quality of roads constructed in soft soil area based on driving comfort[J]. Journal of Hunan University （Natural Sciences），2020，47（7）：120—127. （In Chinese）

[3]? ? 鄒春華，周順華，王炳龍. 有砟軌道路基不均勻沉降引起軌枕空吊的計算方法[J]. 鐵道學報，2013，35（1）：87—92.

ZOU C H，ZHOU S H，WANG B L. Calculation method of unsupported sleepers caused by differential subgrade settlement of ballasted track[J]. Journal of the China Railway Society，2013，35（1）：87—92. （In Chinese）

[4]? ? 吳仲倫. 高速鐵路路基凍脹對軌道不平順的影響分析及動力響應[D]. 北京：北京交通大學，2015：16—20.

WU Z L. Analysis of track irregularity and dynamic response for the influence of high speed railway subgrade frost heaving[D]. Beijing：Beijing Jiaotong University，2015：16—20.（In Chinese）

[5]? ? PAIXAO A，FORTUNATO E，CALCADA R. The effect of differential settlements on the dynamic response of the train-track system：a numerical study[J]. Engineering Structures，2015，88：216—224.

[6]? ? 陳仁朋，王作洲，蔣紅光，等. 基于軌道板抗彎疲勞強度的不均勻沉降控制[J]. 浙江大學學報（工學版），2013，47（5）：796—802.

CHEN R P，WANG Z Z，JIANG H G，et al. Control standard of differential settlement in high-speed railway slab based on bending fatigue strength [J]. Journal of Zhejiang University （Engineering Science），2013，47（5）：796—802. （In Chinese）

[7]? ? 羅強，李鐵，王佳敏，等. 高速鐵路路堤傳遞地基差異沉降特性及控制限值研究[J]. 中國科學（技術科學），2014，44（7）：736—743.

LUO Q，LI T，WANG J M，et al. Analysis on conduction characteristics from embankment and control limits of foundation differential settlement for high speed railway[J]. Scientia Sinica（Technologica），2014，44（7）：736—743. （In Chinese）

[8]? ? 陳兆瑋，孫宇，翟婉明. 高速鐵路橋墩沉降與鋼軌變形的映射關系（Ⅰ）：單元板式無砟軌道系統[J]. 中國科學（技術科學），2014，44（7）：770—777.

CHEN Z W，SUN Y，ZHAI W M. Mapping relationship between pier settlement and rail deformation of high-speed railways—part（Ⅰ）：The unit slab track system[J]. Scientia Sinica （Technologica），2014，44（7）：770—777. （In Chinese）

[9]? ? 陳兆瑋，孫宇，翟婉明. 高速鐵路橋墩沉降與鋼軌變形的映射關系（Ⅱ）：縱連板式無砟軌道系統[J]. 中國科學（技術科學），2014，44（7）：778—785.

CHEN Z W，SUN Y，ZHAI W M. Mapping relationship between pier settlement and rail deformation of high-speed railways—part（Ⅱ）：The longitudinal connected ballastless track system[J]. Scientia Sinica （Technologica），2014，44（7）：778—785. （In Chinese）

[10]? ZHOU W B，NIE L X，JIANG L Z. Mapping relation between pier settlement and rail deformation of unit slab track system[J]. Structures，2020，27：1066—1074.

[11]? 何春燕，陳兆瑋，翟婉明. 高速鐵路路橋過渡段不均勻沉降與鋼軌變形的映射關系及動力學應用[J]. 中國科學（技術科學），2018，48（8）：881—890.

HE C Y，CHEN Z W，ZHAI W M. Mapping relationship between uneven settlement of subgrade and rail deformation in subgrade-bridge transition section and its dynamic application[J]. Scientia Sinica （Technologica），2018，48（8）：881—890. （In Chinese）

[12]? 肖威，郭宇，高建敏，等. 高速鐵路路基不均勻沉降對CRTSⅢ板式軌道受力變形的影響[J]. 鐵道科學與工程學報，2015，12（4）：724—730.

XIAO W，GUO Y，GAO J M，et al. Effect of uneven subgrade settlement on the CRTS Ⅲ slab track stress and deformation of high-speed railway[J]. Journal of Railway Science and Engineering，2015，12（4）：724—730. （In Chinese）

[13]? 裴國史，高建敏，郭宇. 路基不均勻沉降對共享路權有軌電車軌道結構受力的影響[J]. 鐵道科學與工程學報，2018，15（11）：2772—2779.

PEI G S，GAO J M，GUO Y. Influence of uneven subgrade settlement on track structure stress of tramcar on sharing road right[J]. Journal of Railway Science and Engineering，2018，15（11）：2772—2779. （In Chinese）

[14]? 徐慶元，李斌，周智輝. CRTS—Ⅰ型板式無砟軌道線路路基不均勻沉降限值研究[J]. 中國鐵道科學，2012，33（2）：1—6.

XU Q Y，LI B，ZHOU Z H. Study on the limited value for the uneven settlement of subgrade under CRTS-Ⅰ type slab track[J]. China Railway Science，2012，33（2）：1—6. （In Chinese）

[15]? 張克平，石廣田，和振興. 路基不均勻沉降對地鐵A型車輛動力學特性影響研究[J]. 振動與沖擊，2020，39（17）：165—170.

ZHANG K P，SHI G T，HE Z X. Effects of subgrade uneven settlement on dynamic characteristics of metro type A vehicles[J]. Journal of Vibration and Shock，2020，39（17）：165—170. （In Chinese）

[16]? AUERSCH L. Excitation of ground vibration due to the passage of trains over a track with trackbed irregularities and a varying support stiffness[J]. Vehicle System Dynamics，2015，53（1）：1—29.

[17]? BIAN X C，JIANG H G，CHEN Y M，et al. A full-scale physical model test apparatus for investigating the dynamic performance of the slab track system of a high-speed railway[J]. Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit，2016，230（2）：554—571.

[18]? JIANG H G，BIAN X C，CHENG C，et al. Simulating train moving loads in physical model testing of railway infrastructure and its numerical calibration[J]. Acta Geotechnica，2016，11（2）：231—242.

[19]? JIANG H G，BIAN X C，JIANG J Q，et al. Dynamic performance of high-speed railway formation with the rise of water table[J]. Engineering Geology，2016，206：18—32.