改良馬爾可夫模型在節假日客流預測中的應用

徐熠明，趙壽為

（上海工程技術大學數理與統計學院，上海 201620）

0 引言

隨著我國城市軌道交通事業的蓬勃發展，居民開始更多地選擇城市軌道交通作為出行方式，使得地面交通客流擁堵現象得到一定程度的緩解。然而，隨著客流逐漸涌入城市軌道交通，導致客流規模持續攀升［1-4］，給城市軌道交通部門的運營工作帶來了一定壓力，因此對于客流進行合理預測逐漸成為相關部門的工作重點。其中節假日作為一年中的特殊時期，地鐵車站在短時間內容易出現大客流。地鐵運營部門需要提前掌握節假日期間客流量變化趨勢來緩解客流壓力，以此制定合理的客流組織計劃及各種應急方案，以預防一系列事故的發生［3-5］。

目前有許多預測節假日客流的方法，主要分為線性預測和非線性預測兩種。線性預測包括時間序列模型［6］、卡爾曼濾波模型［7-8］等，非線性預測包括非參數回歸、神經網絡模型、支持向量機［9-11］等。由于節假日客流量呈現隨機性、波動性大的特征，使用線性預測模型會使得預測性能變差，而非參數回歸、神經網絡等非線性模型對于樣本量的要求較高，當樣本較少時，預測性能會大大降低。因此，單一模型已無法滿足對預測精度的要求，需要采用組合模型對客流量進行預測。

潘麗等［12］利用灰色模型預測上海鐵路客運量，再結合馬爾可夫鏈模型對預測值進行修正；蔣艷輝［13］分析經典馬爾可夫鏈存在的缺陷，針對其缺陷引入DS 證據理論，建立改進的組合模型；楊小芬［14］利用無偏灰色馬爾可夫模型預測出我國2018-2020 年的國內游客數；王一智等［15］利用歷史數據建立灰色GM（1，1）模型，結合馬爾可夫鏈過程將隨機序列狀態劃分為3 類，并且通過安徽省公路客流量歷史數據預測近兩年的公路客流量；柴武越等［16］通過比較指數平滑模型與ARIMA 模型對上證指數的預測效果，以得到更精準的預測模型；周睿等［17］選取1986-2017 年的數據分別建立指數平滑模型、ARIMA 模型及灰色系統模型，對“十三五”期間（2018-2020 年）全國水產品產量進行預測分析，結果表明3 種模型的預測精度均較高，且預測結果差別不大。由于節假日期間客流量具有不穩定、隨機性強的特征，同時數據樣本較少，綜合考慮上述因素，本文決定采用指數平滑法與馬爾可夫鏈組合模型對城市軌道交通節假日客流量進行預測。

基于歷史節假日客流量數據，本文分析了國慶假期上海軌道交通客流分布特征，首先建立指數平滑法與馬爾可夫組合模型，再根據2018-2019 年度國慶假期數據，發現組合模型預測的不足之處，并結合影響客流預測的相關因素修正預測值，之后使用粒子群算法改進馬爾可夫修正系數，從而提升模型預測精度，最后使用該模型對上海城市軌道交通2020-2022 年國慶假期客流量進行預測。

1 上海軌道交通節假日客流預測模型建立

1.1 指數平滑法

指數平滑法作為時間序列法的一種，由布朗所提出，其作為一種比較傳統的預測方法，通常用于中短期預測。主要計算公式如下：

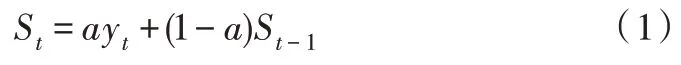
其中，St為在t時刻的平滑值，yt為在t時刻的實際值，St-1為在t-1 時刻的平滑值，a為平滑系數，取值范圍為［0，1］。

根據平滑次數不同，指數平滑法可分為一次指數平滑法、二次指數平滑法和三次指數平滑法等。

本文擬使用指數平滑法研究上海市軌道交通節假日客流量預測問題，基本建模過程如下：

（1）選擇平滑次數。在使用指數平滑法預測之前，根據上海市軌道交通節假日客流量序列特征選擇不同的平滑次數。如果序列無明顯趨勢特征，一般選用一次指數平滑法；如果序列有一定的線性趨勢特征，則適合選用二次指數平滑法；如果序列不僅具有一定的趨勢特征，還帶有一定的季節性，則適合選用三次指數平滑法。3 種平滑法具體公式如下：

（2）確定平滑初值。平滑初值是指指數平滑法的初始值，3 種指數平滑法的初始值在此用表示。一般情況下均取第一項觀測值作為初值，即：

（3）使用式（2）-式（4）進行計算、擬合并預測。

1.2 Holt 指數平滑法

在布朗提出的指數平滑法理論基礎上，霍爾特在1957年提出衍生的Holt 指數平滑模型［18-19］，主要計算公式如下：

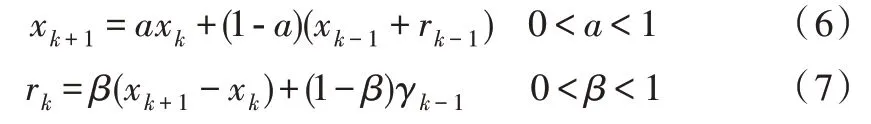
其中，a、β分別為兩個平滑系數，xk+1為修勻后的預測序列，rk為修勻后的趨勢序列。

Holt 指數平滑法本質上就是二次指數平滑法，可預測具有趨勢的時間序列。由于其具有結構簡單、整體效果好等優點，已被普遍應用于經濟管理、控制科學、教育衛生等領域，適用于對含有線性趨勢的序列進行修勻。Holt 指數平滑模型與簡單指數平滑模型的區別在于，其可以處理具有長期趨勢的時間序列，并在處理原始數據之后直接對數據進行預測。

根據上海市軌道交通節假日客流特征，本文使用Holt指數平滑法結合馬爾可夫模型研究上海市軌道交通節假日客流量預測問題。

1.3 馬爾可夫理論

1.3.1 馬爾可夫模型

馬爾可夫理論由俄國數學家馬爾可夫在1906 年提出，后被稱為“馬爾可夫鏈”。“無后效性”是馬爾可夫鏈的最大特點，即在已知系統目前所處狀態的情況下，系統未來所處狀態與過去所處狀態無關，這即是馬爾可夫過程。馬爾可夫模型可表示為：

其中，Xk+1為第k+1 時刻的狀態向量，Xk為第k時刻的狀態向量，P為一步狀態轉移矩陣。

（1）狀態、區間劃分。根據Holt 指數平滑法預測結果，計算原始數據與預測結果的相對誤差，并根據相對誤差對狀態的集中程度進行劃分。

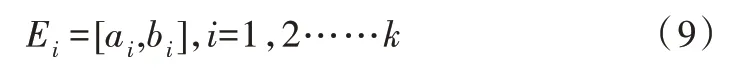
其中，Ei為劃分的狀態區間，ai為被劃分在Ei的相對誤差下限，bi為被劃分在Ei的相對誤差上限。

（2）構建狀態轉移矩陣。由狀態Ei經過一個時期轉移到Ej的一步轉移概率為pij，將所有一步轉移概率排列成一個矩陣，可得狀態轉移矩陣，即：

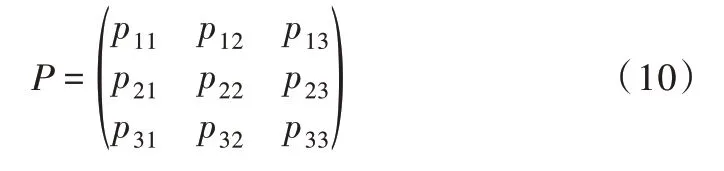
（3）修正預測值。在確定狀態轉移矩陣后，根據某一年所處狀態預測下一年可能出現的狀態，然后對結果用修正公式進行修正。修正公式如下：

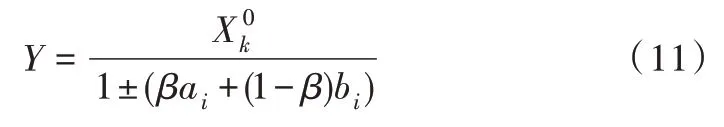
1.3.2 傳統馬爾可夫理論

馬爾可夫過程作為隨機過程理論的重要組成部分，在對于隨機性強和波動性大的時間序列預測上有著良好的適用性，但其具有以下不足：當出現一些影響客流預測的小概率異常情況（如臺風、不定期的大型活動）時，會影響馬爾可夫模型對下一步狀態的預測，從而影響整個運營組織客流預測的工作效率。因此，需要結合影響客流預測的相關因素對下一步狀態區間的預測進行適當修正。同時，傳統馬爾可夫模型對預測值的修正系數β一般取0.5，并不能很好地貼近現實情況，因此可通過粒子群算法計算出最優的修正系數β，從而提升整個組合模型的預測精度。

1.4 粒子群算法

粒子群優化算法（Particle Swarm Optimization，PSO）是一種進化計算技術（Evolutionary Computation），源于對鳥群捕食行為的研究。粒子群優化算法的基本思想是通過群體中個體之間的協作與信息共享來尋找最優解。其優勢在于簡單、容易實現，并且不用調節過多參數，目前已被廣泛應用于函數優化、神經網絡訓練、模糊系統控制等領域。

粒子群算法基本流程如下：

（1）初始化。首先，設置最大迭代次數、目標函數自變量個數、粒子最大速度，并在速度區間和搜索空間上隨機初始化速度和位置。設置粒子群規模為M，每個粒子隨機初始化一個飛翔速度。

（2）個體極值與全局最優解。定義適應度函數、個體極值為每個粒子找到的最優解，從這些最優解中得到一個全局值，稱為本次全局最優解，與歷史全局最優解進行比較并更新。

（3）更新粒子速度和位置。具體公式如下：

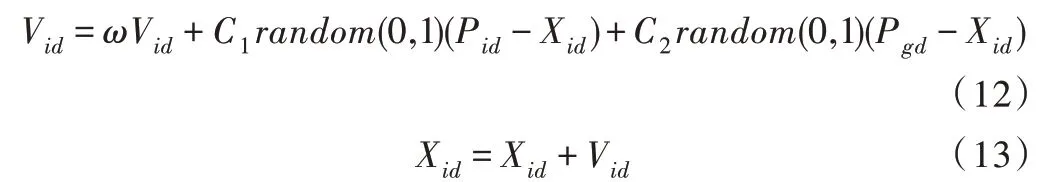
其中，ω 為慣性因子，且ω>0。C1、C2為加速常數，C1為個體學習因子，C2為社會學習因子，random(0,1)為區間［0，1］上的隨機數，Pid為第i個變量個體極值的第d維，Pgd為全局最優解的第d維。

終止條件如下：①達到設定迭代次數；②代數之間的差值滿足最小界限。

1.5 改良的指數平滑馬爾可夫組合模型建立

本文擬采用改良的指數平滑馬爾可夫組合模型研究上海市軌道交通節假日客流量預測問題，具體運算步驟如下：①選取上海市節假日軌道交通客流量序列，使用Holt 指數平滑法擬合預測，得到相關數值；②計算上海市地鐵節假日客流量預測值與實際值之間的相對誤差；③根據相對誤差大小劃定相對誤差對應的區間范圍；④構建馬爾可夫轉移矩陣，并計算預測值對應的狀態區間；⑤根據上海市地鐵節假日客流量預測值對應狀態，使用修正系數對Holt指數平滑法的預測值進行修正，得到預測結果；⑥結合影響客流預測的因素，對步驟⑤中求出的預測結果進行修正；⑦使用粒子群算法對馬爾可夫鏈的修正系數進行優化，提升模型整體預測精度。

2 上海城市軌道交通節假日客流特征分析

鑒于組合模型的獨特優勢，本文擬采用Holt 指數平滑法首先對上海市軌道交通節假日短期客流量進行預測，然后使用馬爾可夫鏈相關理論優化預測結果。本節主要分析近年來上海市軌道交通短期節假日客流量特征，為下一節的預測分析提供參考依據。本文數據來源于上海地鐵微博平臺（https：//www.weibo.com/shmetro）。

我國節假日主要包括元旦、春節、清明3 日假期和國慶節7日假期等，本文選擇國慶節7日假期進行客流特征分析。

2.1 國慶節客流分布特征

以上海2011-2017 年國慶假期軌道交通全線客流量分布為例，國慶假期各天客流量分布趨勢及歷年全線客流總量分布趨勢分別如圖1、圖2 所示。

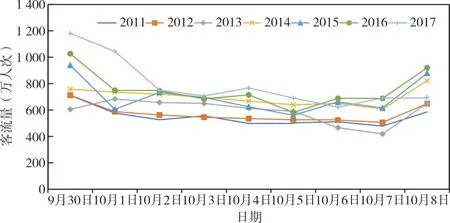
Fig.1 Passenger flow of Shanghai rail transit during each day of National Day holiday from 2011 to 2017圖1 上海城市軌道交通2011-2017 年國慶假期各天全線客流量

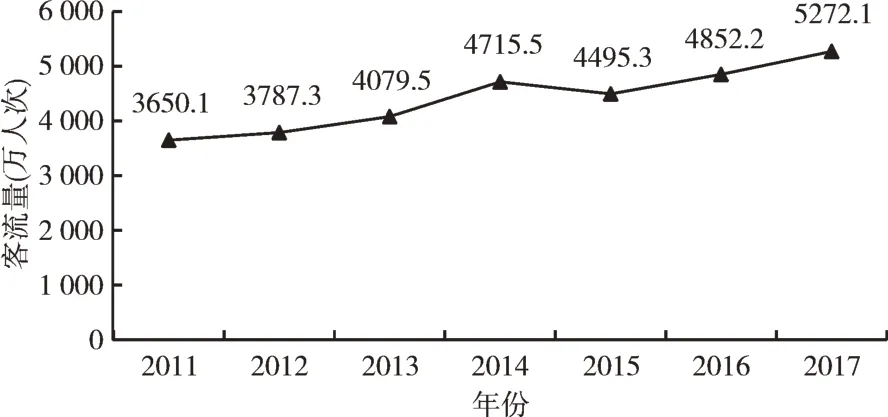
Fig.2 Total passenger flow of Shanghai rail transit during the National Day holiday from 2011 to 2017圖2 上海城市軌道交通2011-2017 國慶假期客流總量

從圖1 可以看出，國慶假期客流量分布大致呈先減后增趨勢，假期前一天和后一天的客流量明顯高于國慶假期客流量，2011-2017 年節假日的客流量趨勢也大致相同。

從圖2 可以看出，自2011 年以來，在國慶假期選擇上海市軌道交通作為出行方式的人數雖有波動，但總體上呈線性遞增趨勢。

根據以上客流特征分析可得，國慶假期的客流量不僅具有一定的波動性和隨機性，也呈現一定的趨勢性。同時，由于上海市軌道交通客流量數據樣本較少，單一模型已無法準確預測客流量，因此本文使用Holt 指數平滑法與馬爾可夫組合模型進行預測。

2.2 節假日客流預測主要影響因素

（1）天氣變化。由于城市軌道交通具有獨立的運行空間和相對封閉的候車環境，所以受天氣變化的影響較小。然而，由于人們在節假日期間出行的自由性，在惡劣天氣條件下，很多人會減少出行，從而使客流量大幅減少。因此，節假日客流量受臺風、暴雨等惡劣天氣的影響較大。

（2）大型活動的舉辦。在節假日期間舉辦的不定期的大型活動（如國慶期間的旅游節、祖國誕辰周年慶等）會使軌道交通出行客流量大幅增加，從而影響客流預測精度。

（3）外來人員返程日期的變化。隨著城市生活節奏的加快，許多在節假日期間返鄉的外來務工人員可能會提前1～2 天返回城市，客流量也會隨之出現一定的轉移，使得客流預測出現偏差，在預測過程中也應該注意這一點。

（4）其他因素。如地震、海嘯、大型傳染病等極其罕見的現象，雖然很少發生，但也可以適當考慮進客流預測工作中。

在上述影響因素中，天氣變化等因素容易使模型預測結果偏大，而大型活動等因素容易使模型預測結果偏小。本文根據實際情況調整受到各因素影響的特定日期的相對誤差狀態區間，從而提高模型預測精度。

3 模型預測實例

3.1 數據選取與說明

本文選擇上海城市軌道交通2011-2017 年國慶假期的各日客流量作為原始數據，構建Holt 指數平滑法與馬爾可夫組合模型，并結合影響客流預測的相關因素對預測精度差進行修正，最后使用粒子群算法改良整個馬爾可夫組合模型的修正系數，以提升模型預測精度。

3.2 Holt 指數平滑法預測

針對2011-2017 年國慶假期客流數據，使用Holt 指數平滑法進行參數計算及初步預測。具體預測過程如下：以2011-2017 年10 月1 日的歷史數據為例，2011-2017 年國慶節第一天（10 月1 日）客流數據的原始序列為［577.0，587.8，683.4，735.7，605.2，748.6，751.0］，對原始序列進行Holt 指數平滑，利用R 軟件求得指數平滑擬合值及相對誤差如表1 所示。

3.3 馬爾可夫鏈優化

從表1 可以看出，國慶第一天客流量相對誤差的最大值為14.96%，最小值為-14.14%。當Holt 指數平滑法擬合值與真實值十分接近時，不予修正，即誤差在［-0.5%，0.5%］之間時，不對原來的預測值進行修正，由此劃分3 個狀態區間。國慶第一天客流量預測結果的狀態區間分別為E1（-14.14，-0.50］、E2（-0.50，6.28］、E3（6.28，14.96］，如表2 所示。

Table 1 Holt exponential smooth fitting value and relative error（first day of National Day）表1 Holt 指數平滑擬合值及相對誤差（國慶第一天）

Table 2 State interval of relative error between exponential smooth?ing predicted value and real value（first day of National Day）表2 指數平滑預測值與真實值相對誤差狀態區間（國慶第一天）

3.3.1 各年狀態區間劃分

對各年狀態區間進行劃分，如表3 所示。

Table 3 Division of state intervals of relative errors between exponen?tial smoothed prediction and real values（first day of National Day）表3 指數平滑預測值與真實值相對誤差狀態區間劃分（國慶第一天）

3.3.2 狀態轉移矩陣構建

根據表3 相對誤差的狀態區間劃分，可得到相對誤差序列的狀態轉移頻數，然后計算由狀態Ei轉移到Ej的概率，得到國慶第一天客流量的一步狀態轉移矩陣為：

3.3.3 計算預測值與模型預測精度對比

根據以上的狀態區間劃分及構建的狀態轉移矩陣，可得到2018 年和2019 年國慶客流量相對誤差最可能位于的狀態區間，如表4 所示。單一Holt 指數平滑法與組合模型的預測精度對比如表5、表6 所示。

Table 4 National Day passenger flow relative error state interval表4 國慶客流量相對誤差狀態區間

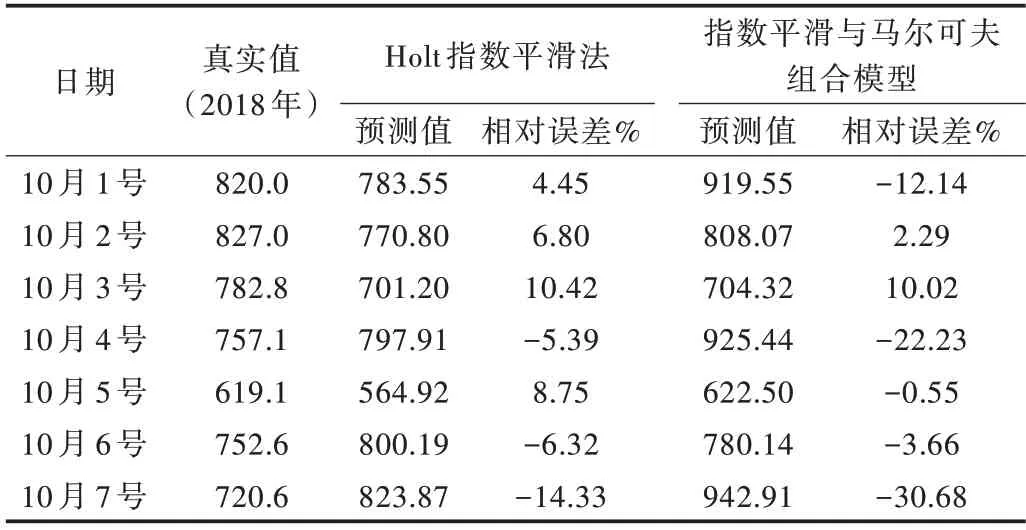
Table 5 Comparison of prediction accuracy between single Holt exponen?tial smoothing method and combined model（National Day holiday 2018）表5 單一Holt指數平滑法與組合模型預測精度對比（2018年國慶假期）

Table 6 Comparison of prediction accuracy between single Holt exponential smoothing method and combined model（National Day holiday in 2019）表6 單一Holt指數平滑法與組合模型預測精度對比（2019年國慶假期）

綜合表5、表6 可知，指數平滑法與馬爾可夫組合模型對國慶假期中10 月1 號、10 月4 號、10 月5 號的客流預測嚴重失準，因此需要結合影響客流預測的相關因素對預測結果進行修正。通過調查歷史天氣、大型活動等信息，可整理得到影響上海當天客流預測的重要因素，如表7 所示。

Table 7 Factors affecting the accuracy of passenger flow forecast and passenger flow forecast changes表7 影響國慶客流預測的因素及客流預測值變化情況

由表7 可知，臺風等惡劣天氣會使客流量大幅減少，從而使得預測值偏大。大型動漫活動的舉辦會使預測值偏小，返滬客流的轉移也會影響到客流預測，因此需要對客流量預測相對誤差狀態區間和預測結果進行一定的修正。以2019 年10 月1 日為例，由于受到臺風影響，其預測相對誤差狀態區間應由E3 修正為E1。對2018、2019 年嚴重失準的預測值進行修正后，模型修正前后預測精度對比如表8 所示。

Table 8 Prediction accuracy comparison before and after model correction表8 模型修正前后預測精度對比

通過表8 可以看出，經過修正后的指數平滑法與馬爾可夫組合模型的相對誤差均明顯低于修正前的組合模型，說明改良后的指數平滑法與馬爾可夫組合模型的預測更加合理、有效，可適用于軌道交通客流量短期預測。

3.4 基于粒子群算法的馬爾可夫組合模型優化

使用MATLAB 軟件運行算法程序后，可得到優化修正系數后的模型預測結果。傳統馬爾可夫組合模型與粒子群算法改良模型預測精度對比如表9 所示。

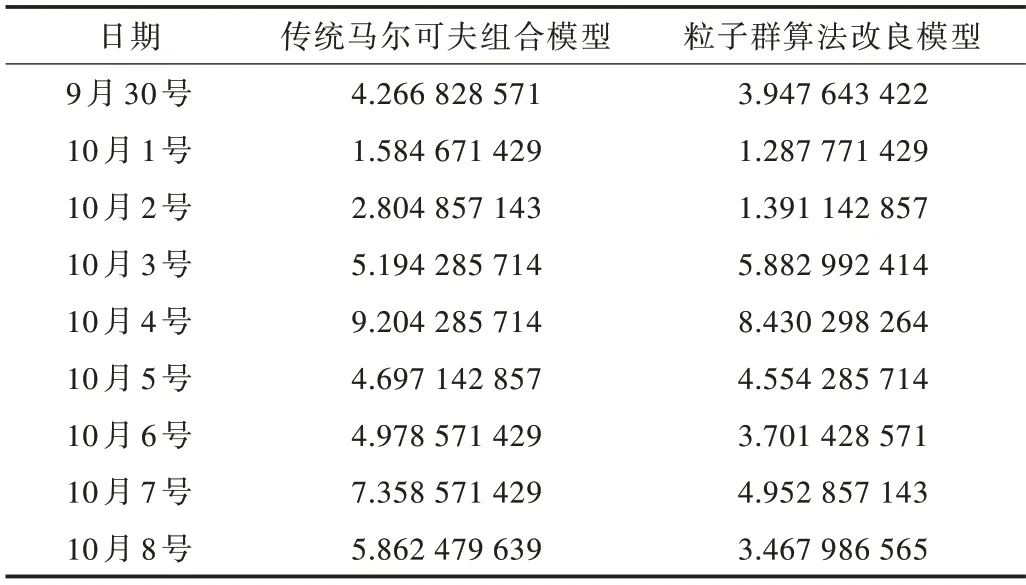
Table 9 Prediction accuracy comparison of traditional Markov combination model and improved model of particle swarm algorithm（mean absolute error）表9 傳統馬爾可夫組合模型與粒子群算法改良模型預測精度對比（平均絕對值誤差）

由表9 可知，經過粒子群算法優化修正系數后的馬爾可夫模型取得了良好的預測效果，其平均絕對值誤差均小于傳統馬爾可夫組合模型。改良模型的預測結果更貼近于真實值，預測精度也得到了進一步提升。將其應用于上海城市軌道交通節假日客流量預測中，可為預測工作提供一種新思路。

3.5 2020-2022 年國慶客流量預測

采用改良后的馬爾可夫組合模型進行預測，得到上海城市軌道交通2020-2022 年國慶假期各天客流量如圖3 所示。從圖中可以看出，改良后的馬爾可夫組合模型預測結果與2011-2017 年國慶假期的客流趨勢走向大致相同，即均呈現兩邊高、中間低的趨勢，表明修正后的組合模型預測精度較高。

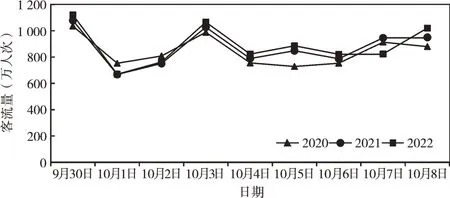
Fig.3 Passenger flow of Shanghai rail transit during each day of National Day holiday from 2020 to 2022圖3 上海市軌道交通2020-2022 年國慶假期各天客流量

3.6 建議

針對以上客流預測結果，本文給出如下建議：

（1）針對節假日期間出現由于大型活動導致客流量大幅增加的情況，運營組織需要提前作好應對措施，對客流進行疏導，避免因客流量過大導致線路癱瘓的情況發生。

（2）針對節假日期間出現因受到臺風等惡劣天氣影響導致客流量急劇減少的情況，運營組織應適當減少車輛的調配，或在行車計劃中適當多安排一些大小交路，從而使運輸能力最大化，節省運營車輛維護成本。

4 結語

本文采用指數平滑法與馬爾可夫組合預測模型對上海城市軌道交通節假日客流量進行預測，并結合影響客流預測的相關因素和粒子群算法對預測結果進行優化。結果顯示，修正后的馬爾可夫組合模型在預測2018-2019 年上海城市軌道交通節假日客流量上具有更高的預測精度，該模型可應用于上海城市軌道交通節假日客流量預測。當然，本文只針對城市軌道交通全線客流量進行了預測，尚未對不同類型車站的客流量進行更詳細的預測。因此，在目前研究的基礎上，可進一步針對上海城市軌道交通不同類型車站的客流量進行分析與預測。