基于社交媒體數據的貝葉斯A/B 檢驗
李薛莎,付英姿,薛 茜,夏思琴
(昆明理工大學 理學院,云南 昆明 650093)
0 引言
A/B 檢驗主要用于考察相對于原方案A,改進方案B 是否更優。其基本思想是從包含實驗組和對照組的平行實驗中收集數據,并利用檢驗手段評估兩個方案中哪一組成功率更高,從而幫助決策者作出科學判斷。目前,A/B 檢驗已被廣泛應用于生物醫學、藥學、心理學、社會行為學等多個領域。例如,醫藥公司常常利用A/B 檢驗考察所研發的新藥相較于傳統藥物,在療效方面是否更顯著。此外,A/B檢驗還可用來衡量心理干預是否能夠加快促進病人痊愈。在大數據背景下,社交媒體數據蘊含著巨大的商業價值,A/B 檢驗已被成功地運用到商業網站點擊率預測以及精準營銷方案的投放等多個應用場景,然而從國內外相關研究成果看,大多數研究還處于起步狀態。由此可見,對A/B 檢驗問題的研究有著巨大的探索空間和價值。
在經典的假設檢驗問題中,A/B 檢驗可以理解為關于零假設的顯著性檢驗(Null Hypothesis Significance Testing,NHST),其相應的p值表示樣本在原假設下出現極端事件的概率,即觀測到的顯著性水平。當p值小于規定的顯著性水平α時,則拒絕原假設;否則,接受原假設。隨著研究的深入,人們發現經典的檢驗方法存在諸多局限性,例如,Wagenmakers[1]研究表明,基于p值的假設檢驗存在邏輯和統計限制,它易受主觀意圖的影響,不能很好地量化統計證據;Gallistel 等[2]、Rouder 等[3]進一步指出,基于p值的經典檢驗方法依賴于未觀察到的數據,難以對原假設提供足夠的支持。為此,Malek 等[4]對基于p值的經典檢驗方法作出改進,使其能夠隨著數據的增加而自動進行校正,更多相關研究成果可參見文獻[5-7]。
眾所周知,貝葉斯方法的優勢在于它能夠借助于優良的先驗信息以提高檢驗精度,同時對樣本量沒有過多的限制。從貝葉斯的角度看,貝葉斯A/B 檢驗的關鍵是比較兩種方案下后驗概率的大小,其本質是通過引入貝葉斯因子以實現模型間的比較和選擇。早在1935 年,Jeffreys[8-9]率先提出用于標準假設檢驗問題的貝葉斯因子,這為貝葉斯A/B 檢驗奠定了基礎。隨后,Kass 等[10-11]改進了Jeffreys 所提出的近似貝葉斯因子的方法,并將其應用于兩個二項式比例相等性的檢驗問題上;Alexander 等[12]研究了兩個常見的基于貝葉斯因子假設檢驗的應用場景,即檢驗正態均值的零度(即貝葉斯t檢驗)和檢驗相關性的零度問題,并將其應用于心理學實驗。然而,從現有研究成果看,目前大多數研究僅考慮了兩個方案下成功概率是否相等的問題,還難以確定出最優方案。為此,本文擬考慮如下3 類假設檢驗問題,即:①H0:P1=P2,H1:P1≠P2(兩個方案是否相等);②H0:P1=P2,H+:P1
網頁改版能否帶來更多點擊率,從而為公司帶來更大利潤一直都是網絡公司關注的核心問題。為此,本文以硅谷前沿科技教育平臺優達學城(Udacity)提供的新舊版本網頁點擊轉換率數據為例,建立了基于貝葉斯因子的A/B檢驗并挑選出最優方案。具體地,首先建立貝葉斯框架下的二元Logistic 回歸模型以刻畫網頁改版前后的點擊率;在后驗概率的比較方面,其關鍵在于貝葉斯因子的計算,注意到貝葉斯因子是不同假設下邊際似然函數的比值,問題就進一步歸結為邊際似然的計算。為此,采用拉普拉斯近似方法解決上述問題,特別地,對于單邊假設(II)和(III)而言,本文在拉普拉斯近似的基礎上增加了重要性抽樣技術以更好地擬合尖峰厚尾分布。研究結果表明,對網頁的改版并不能有效地增加用戶點擊率。
1 模型與方法
1.1 假設檢驗問題提出
假設有兩個方案A 和B,方案A 表示原方案,方案B 則是對A 作出某些改進或調整后形成的新方案。令p1為方案A 的成功率,p2為方案B 的成功率。A/B 檢驗的目的是考察新方案對于原方案而言,在成功率上是否有所提高,與之對應的假設檢驗問題為:原假設H0:P1=P2,備擇假設H1:P1≠P2。若接受原假設,則認為A、B 方案沒有區別;否則,認為兩個方案有區別。注意到,上述假設檢驗問題僅關注了A、B 方案是否等價,而無法確定哪一個方案更優。為此,本文在經典檢驗問題的基礎上又引出如下兩個單邊檢驗問題,分別為:H+:P1
1.2 二項分布與Logistic 回歸
在具體實施過程中,A/B 檢驗從包含實驗組(A)和對照組(B)的平行實驗中收集數據,并根據樣本計算出不同方案下的成功率以確定最優方案。假設Y1為方案A 下的成功次數。顯然,Y1服從成功率為P1的二項分布,即其中N1表示方案A 的實驗總次數。同理,假設Y2為方案B 下的成功次數,即其中N2表示方案B 的實驗總次數。對于二項分布而言,Logistic 回歸是刻畫二項分布中成功概率P的通用選擇。為此,本文考慮如下典則聯系函數
經典的假設檢驗問題需要比較兩個方案在成功率上是否相等,即需要考察假設檢驗問題H0:P1=P2,H1:P1≠P2,注意到:
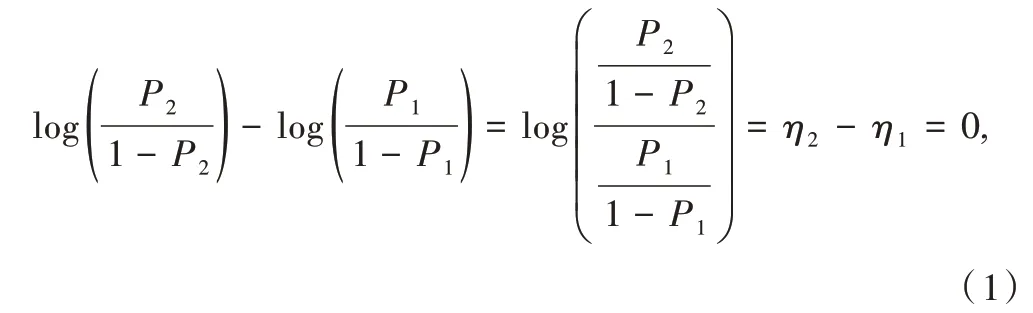
可見,原假設檢驗問題與檢驗H0:η2-η1=0,H1:η2-η1≠0 是等價的。進一步地,若令ψ=η2-η1,原假設檢驗就退化為檢驗ψ是否為0 的問題。為了檢驗兩個二項式比例是否相等[11],可構建二元Logistic 回歸模型如下:
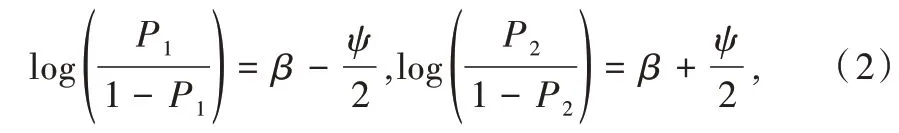
結合式(1)、式(2)則有:
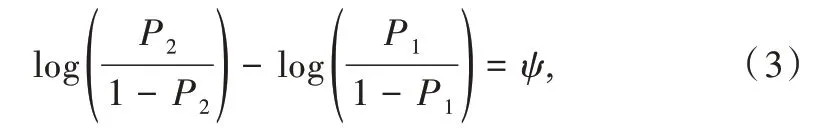
①H0:P1=P2,H1:P1≠P2→H0:ψ=0,H1:ψ≠0;
②H0:P1=P2,H+:P1
③H0:P1=P1,H-:P1>P2→H0:ψ=0,H-:ψ<0。
1.3 基于貝葉斯 檢驗的后驗推斷
1.3.1 貝葉斯因子及邊際似然計算
在貝葉斯框架下,貝葉斯因子[13](Bayes Factor)量化了數據對原模型和備選模型的支持程度,是模型比較和選擇的重要統計量。其定義為:對于兩個模型H0、H1,其中H0表示原模型,H1表示競爭模型,假設數據集Y來自于H0、H1中的其中一個,分別對應于邊際似然函數:和則有:

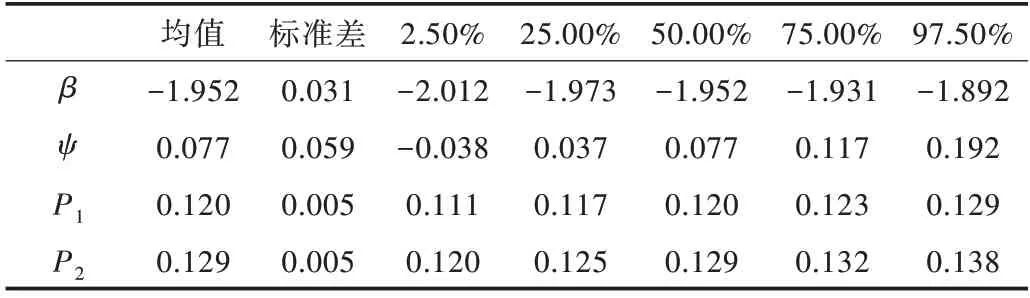
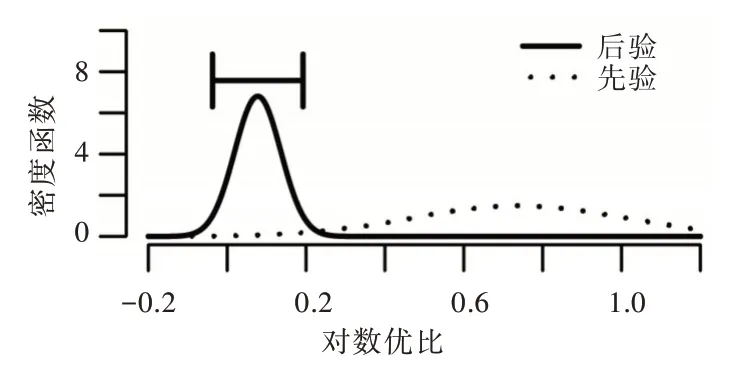
其被稱為用于比較原模型H0和備擇模型H1的貝葉斯因子。對于貝葉斯因子的解釋,一般認為,當BF10<1 時,表明有證據支持原模型,即H0優于H1;當1 針對本文考慮的3 類假設檢驗問題:①H0:ψ=0,H1:ψ≠0;②H0:ψ=0,H+:ψ>0;③H0:ψ=0,H-:ψ<0。其 對應的貝葉斯因子分別為: 如上所述,A/B 檢驗關注的是新方案相對于原方案是否有所改進。從貝葉斯的角度看,問題歸結于考察上述3類假設檢驗的后驗概率是否有所提升的問題。由貝葉斯定理可知,后驗概率比即后驗似然比與貝葉斯因子之間存在如下關系: 其中,P(Y|H0)表示原模型的邊際似然函數,表示備擇模型的邊際似然函數。 本文分別給出了3 類假設檢驗問題下貝葉斯因子的具體表達式: (1)考慮H0:ψ=0,H1:ψ≠0,貝葉斯因子為: (2)考慮H0:ψ=0,H+:ψ>0,貝葉斯因子為: (3)考慮H0:ψ=0,H-:ψ<0,貝葉斯因子為: 1.3.2 拉普拉斯近似 由式(5)可知,后驗似然比由貝葉斯因子和先驗似然比兩部分構成,而先驗似然比通常事先指定,于是問題的關鍵就歸結為如何計算貝葉斯因子。由式(6)—式(8)可知,貝葉斯因子定義為兩個競爭模型的邊際似然函數的比值,其計算涉及難以處理的復雜積分。為此,本文將采用拉普拉斯近似[14-15](Laplace Approximation)的方法解決復雜積分求解問題。 拉普拉斯近似的基本思想是將難以求解的積分問題轉換為正態分布形式,以降低復雜積分求解難度。這種近似方法適用于被積函數是單峰時的情形,以確保拉普拉斯近似逼近收斂到唯一一個最大值。眾所周知,泰勒展開可以通過一個點對函數進行觀察,基于此,拉普拉斯近似通過對被積函數在眾數點(mode)的鄰域內進行二階泰勒展開以近似積分,更多拉普拉斯近似的相關細節可參考附錄。 針對情形(1),考慮假設H0:ψ=0,由于在H0下模型只含有參數β,根據拉普拉斯近似有: 考慮備擇假設H1:ψ≠0,此時模型中含有兩個參數待估參數β和ψ,類似地,根據拉普拉斯近似有: 基于式(9)、式(10),可計算得到貝葉斯因子BF10,接下來將考慮BF+0和BF-0的計算問題。 1.3.3 重要性抽樣 顯然,單邊假設H+是下界為0 的截尾正態分布,H-是上界為0 的截尾正態分布,此時若繼續使用拉普拉斯近似方法,將會導致有偏甚至無效的統計推斷結論。為此,本文引入重要性抽樣[16-17]近似表示H+和H-下的邊際似然函數。 重要性抽樣突顯了被積函數中重要區域的貢獻,是蒙特卡洛方法(Monte Carlo,MCMC)中最有效的方差縮減技術。其主要思想是利用一個分布較簡單的函數(重要性密度函數)中大量樣本點的加權平均以近似積分過程。在模型H+、H-下分別令經驗表明,當多元t分布的自由度為5 時,對于尖峰厚尾的分布具有良好的擬合效果。因此,本文選取自由度為5 的多元t分布作為重要性密度函數。 針對情形(2),由于模型H0邊際似然函數在式(10)已計算出,因此只需計算模型H+的邊際似然函數,其近似結果為: 本文利用重要性重抽樣(SIR)方法獲取后驗樣本,基本思想是在重要性抽樣函數中抽取樣本,通過加權修正抽樣概率,使樣本中的每個觀測點依據概率再次抽樣,從而獲得后驗樣本。具體步驟如下: (1)產生樣本。從給定參數的多元t分布函數tin中抽取N個獨立同分布的樣本β(n)、γ(n),其中n=1...N。 (2)計算重要性權重: (4)重采樣及算法監控。使每一個觀測點以概率vn出現在N個樣本中,同時有放回地重新抽取樣本,直至的分布收斂到目標后驗分布。在收斂性方面,本文采用EPSR(Estimates Potential Scale Reduction)值以監控算法收斂情況。 針對情形(3),由于模型H0邊際似然函數在式(10)已給出,只需計算模型H-下的邊際似然函數,其近似結果為: 模型H+和H-對應的邊際似然函數近似計算結果如式(11)、式(13)所示,結合模型H0的邊際似然函數近似結果,可分別計算出貝葉斯因子BF+0和BF-0。 1.3.4 先驗設置 如上所述,當β和ψ為零正交參數時,β不同的先驗設置對貝葉斯因子影響很小。然而,ψ反映出備擇假設與零假設之間的差異,因此對ψ的先驗設置至關重要。本文對參數β和ψ均考慮正態先驗,對于參數β,其先驗設定為標準正態分布,即β~N(0,1) 。對于模型H+:ψ>0,參數ψ的分布是一個下界為0 的截尾正態分布,而對于模型H-:ψ<0,ψ的分布是一個上界為0 的截尾正態分布。因此,本文考慮為了得到超參數μψ和σψ的具體取值,考慮如下最小二乘法(Least-squares minimization)以估計參數μψ、σψ。 其中,qi,i=1,...I表示分位數,pi,i=1,...I表示分位數對應的概率值表示參數ψ的先驗累計分布函數,更多計算細節可參考文獻[18]。 基于貝葉斯因子,結合先驗概率比,可計算出后驗概率比。由于貝葉斯方法具有內在一致性,即上一步的后驗可作為下一步的先驗,通過考察不同先驗設置下后驗概率的變化情況,可以量化數據對不同競爭模型的支持程度,從而進行模型與方案之間的選擇。 本文利用硅谷前沿科技教育平臺優達學城(Udacity)提供的新舊版本網頁點擊轉換率數據為例,說明本方法的適用性。該公司在舊版網頁的基礎上開發了一款新的網頁,將新版網頁投放到客戶端,嘗試增加用戶點擊率,期望讓更多的用戶愿意為產品付款,同時幫助公司了解實施新方案能否增加公司效益。該數據集共包含10 000 個樣本點,涉及舊版網頁(Old Page)點擊轉換率、新版網頁(New Page)點擊轉換率,記方案A 表示公司采用舊版網頁,方案B 表示公司采用新版網頁,并將用戶成功跳轉網頁并付款的事件記為“1”,反之記為“0”。 本文選取5 000 個實驗組使用舊版網頁,5 000 個對照組使用新版網頁,記錄每組中用戶的頁面使用情況。公司感興趣的是網頁改版能否增加點擊率,從而給公司帶來利潤。假設公司預期使用新版網頁點擊率提高15%,這里的15%對應著絕對風險的先驗中位數,其置信水平為95%的置信區間為[0.025,0.275]。本文為參數β、ψ分配正態分布先驗。如上所述,參數β先驗的改變對貝葉斯檢驗結果影響不大,因此考慮將其設置為標準正態分布,即β~N(0,1),而參數ψ反映出備擇假設與零假設之間的差異,故ψ的先驗設置至關重要。Howard 等[19]表明當成功概率P1非常(小)大時,成功概率P2也會非常(小)大,且二者具有相互依賴的關系。在此基礎上,本文同樣考慮,并使用最小二乘法估計超參數μψ、σψ,考慮取q=(0.025,0.15,0.275),則對應的概率值p=(0.025,0.5,0.975),結合式(14)利用最小二乘估計計算出先驗設置結果如表1 所示。 Table 1 Results of prior setting表1 先驗設置結果 由上述分析可知,方案A 與B 相等、方案B 優于A、方案B 劣于A 分別對應于假設檢驗問題H0:ψ=0、H+:ψ>0、H-:ψ<0。不失一般性,將先驗概率的初值賦為貝葉斯因子的計算結果分別為BF10=0.011,BF+0=0.01,BF-0=0.379,均小于1,表明有證據支持零假設,即P1=P2。根據計算出的貝葉斯因子,在給定先驗概率的情形下,計算出不同假設模型下的后驗概率,結果如表2 所示。 Table 2 Posterior probabilities of different models表2 不同模型下的后驗概率 通過表2 可以發現,模型H0:ψ=0(p1=p2)的后驗概率較先驗概率提升較明顯,概率由0.5 增長到0.837,模型H+:ψ>0(p1 觀察表3 可以看出,P1的估計值為0.120,P2的估計值為0.129,二者差距不明顯,數據表明支持零假設H0:ψ=0,即P1=P2。因此,有理由認為改進后的網頁并不能給公司增加預期點擊率及利潤回饋,但實際上存在這樣一種可能,即新版網頁確實能夠增加網頁點擊率,但是改善效果并沒有公司預期高。為了評估這種可能,本文利用貝葉斯絕對風險度量這種可能性,結果如圖1 所示。 Table 3 Results of parameter estimation表3 參數估計結果 Fig.1 Absolute risk圖1 絕對風險 其中,后驗中值為0.008,95%的置信區間為[-0.004,0.021]。從圖1 可以看出,在兩個成功概率的差值不完全為0 的情況下,絕對風險的后驗中值小于先驗中值。因此,可以認為對網頁進行改版確實可以增加網頁點擊率,但是改善的效果遠低于公司預期。 由此可知,參數ψ表示對數優比,它可以反映出其他假設與零假設H0之間的差異程度。為了進一步證實改版網頁對增加點擊率是否有效,本文繪制出關于參數ψ(對數比值比)的先驗分布與后驗分布圖像,如圖2 所示。 Fig.2 Log odds ratio圖2 對數優比 其中,后驗中值為0.078,95% 的置信區間[-0.038,0.195]。從圖2 可以看出,對數優比的后驗分布中值小于先驗分布中值。可以看出,Udacity 平臺推出新網頁后,對網頁點擊率有一定促進作用,但是低于公司預期。因此,公司可以考慮不對網頁進行更換。 本文以硅谷前沿科技教育平臺優達學城(Udacity)提供的新舊版本網頁點擊轉換數據為例,通過構建完整貝葉斯框架下的二元Logistic 回歸模型與后驗模擬算法對新舊版本網頁點擊率進行A/B 檢驗。研究結果顯示,公司改版后的網頁對于增加點擊率從而增加公司收益的作用并不明顯,因此對于網頁更換可以酌情考慮。針對不同的領域,該方法可以應用于醫療行業、心理學行業等,以幫助解決實際問題。本文主要研究了貝葉斯框架下A/B 檢驗在商業方面的應用及推廣,其研究成果對于企業網頁改版具有重要參考價值及指導意義。然而,本文僅考慮了基于兩組方案數據(A 組和B 組)的貝葉斯A/B 檢驗,事實上,為了考慮更多的可能性,通常需要比較兩個以上的方案,從而選擇其中最優的一個方案。例如,當實驗方案組別增加至3組時(A 組、B 組、C 組),可以使用貝葉斯損失函數衡量不同方案成功概率的大小,從而選擇最優方案[20]。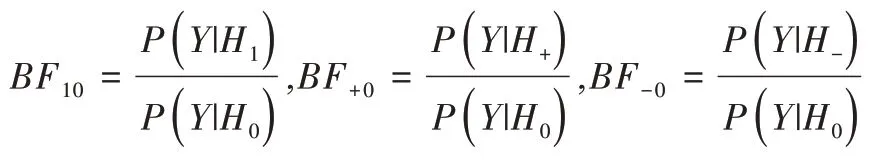

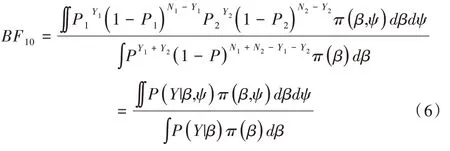
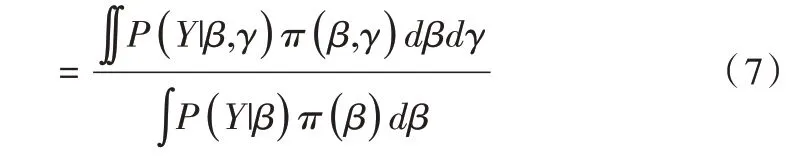
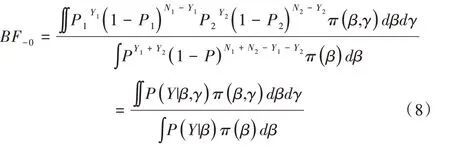



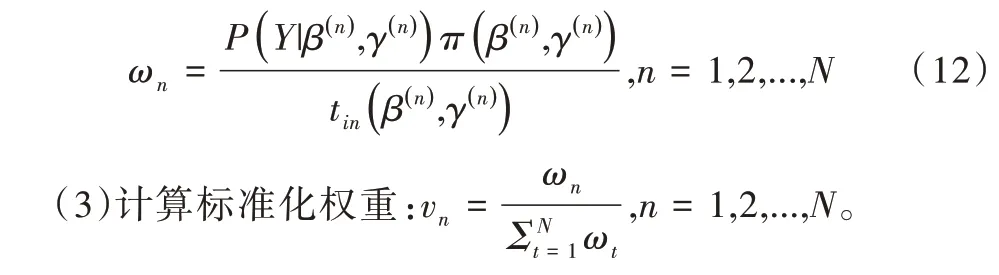
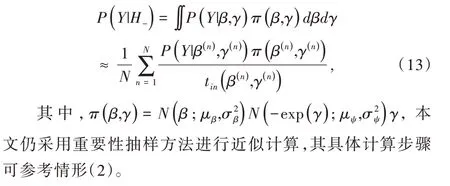

2 實例分析



3 結語

