分層排土場邊坡降雨入滲過程及穩定性分析

蔡文倩，王建德，姜立春

(1.華南理工大學 安全科學與工程研究所，廣州 510640；2.廣東省安全生產科學技術研究院，廣州 510060)

連續強降雨是礦山排土場邊坡工程地質災害的主要誘因，降雨入滲是排土場邊坡失穩的主要誘因[1]。嶺南沿海地區雨量充沛，降雨時間短、強度大，對排土場邊坡穩定性的影響更加復雜。分層碾壓排土是提高礦山排土場邊坡穩定的主要措施[2]，在降雨作用下，土體體積含水率的增加容易增大介質顆粒的下滑力，極易造成邊坡整體失穩[3-5]，因此，開展降雨入滲條件下土體內體積含水率與降雨入滲深度的變化，對分層排土場邊坡穩定性研究，具有十分重要的意義。

長期以來，國內外學者主要從降雨入滲過程[6-8]和安全系數[9-11]兩個方面，開展降雨作用下邊坡穩定性影響研究。在降雨入滲過程方面[6-8]，王文焰等[6]將飽和層與傳導層統一視為飽和區，推導出適用于黃土土體的積水入滲模型，描述非飽和黃土中的水分入滲過程。MA等[7]引入飽和系數來確定濕潤區的含水量和導水率，基于Green-Ampt入滲模型，較好地揭示了均質土體的入滲速率、累積入滲量和濕潤鋒的運動過程。張杰等[8]針對黃土入滲水分剖面變化特征，基于達西定律和雨水入滲質量守恒方程，推求入滲深度和時間的模型關系。在邊坡安全系數方面[9-11]，WANG等[9]針對常用條分法分析邊坡穩定性存在的缺陷，提出了一種基于條帶之間幾何關系的土質邊坡可靠度分析和安全系數計算方法。王奭[10]采用有限元極限分析方法結合強度折減理論，定義無量綱參數P，求解邊坡安全系數，判定均勻土質邊坡穩定性。ARYA等[11]采用數值模擬方法，研究給出孔隙水壓力與裂縫位置對邊坡安全系數的影響關系。總體而言，相關研究主要集中于對單層均質土坡的研究，鮮有涉及降雨入滲條件下分層排土場邊坡的問題。

本文擬采用分層邊坡降雨入滲深度計算方法，結合土力學試驗，研究不同降雨條件作用下，嶺南某露天礦山分層排土場邊坡的體積含水率、入滲深度以及安全系數等變化過程，分析其穩定性，利用現場監測數據，驗證分析結果的可靠性，為降雨入滲分層邊坡的災害防治提供理論依據。

1 理論計算

1.1 分層邊坡降雨入滲深度Hf

對于降雨入滲誘發分層結構邊坡失穩而言，滑裂面通常出現在不同土(巖)層的交界面區域。究其原因，當濕潤峰(濕潤峰是指水分下滲過程中，土壤被濕潤的先頭部位與干土層形成的明顯交界面)下移至分層交界面時，由于各分層土(巖)間滲透系數不同，容易在交界面區域出現土體飽和問題，進而產生滑移現象誘導邊坡發生失穩破壞。

研究表明[12-14]，要研判土(巖)質邊坡破壞模式與分布位置，關鍵是要確定雨水的入滲深度，雨水的入滲深度是由土體的滲透系數決定，因此研究降雨條件下土體滲透系數對入滲深度的影響是評價邊坡穩定性的重要方面。圖1為根據礦山排土場現狀地形圖和原始地形圖建立典型剖面得到的分層邊坡模型。其中，(a)為排土場邊坡實景圖，(b)為排土場邊坡剖面圖，(c)為降雨條件下分層邊坡體積含水率θs分布示意圖。

在圖1(c)中：L1，L2分別為不同土層的垂直厚度；θ1i、θ2i、θ3i分別為土層1、土層2、強風化巖的初始體積含水率；θ1s、θ2s、θ3s分別為不同土層的飽和含水率；Δθ1，Δθ2，Δθ3分別為設定的不同分層土體內飽和含水率與初始含水率的差值。

1.1.1 降雨入滲兩層邊坡深度

1)當降雨強度q小于滲透系數K1，且濕潤鋒位于土層1時，濕潤鋒到達土層1、2交界面的時間t1為：

(1)

此時，降雨入滲的深度Hf為：

(2)

2)當降雨強度q大于滲透系數K1，且濕潤鋒位于土層1時，濕潤鋒到達土層1、2交界面的時間t1為：

(3)

此時，降雨入滲的深度Hf為：

(4)

1.1.2 降雨入滲多層邊坡深度

同理可得，濕潤鋒到達第i，i+1土層交界面的時間和降雨入滲深度。

1)當降雨強度q小于i土層的滲透系數Ki時，根據式(1)分別計算雨水在不同土層中的入滲時間t1，t2，t3，…，ti-1，再結合式(2)計算濕潤鋒到達第i，i+1土層交界面的時間ti，即為：

(5)

由式(5)得到濕潤鋒到達第i、i+1土層交界面的時間ti。將計算結果代入式(2)，可得降雨入滲深度Hf。

(6)

2)當降雨強度q大于第i土層滲透系數Ki，且濕潤鋒位于第i土層中，同理可得濕潤鋒到達第i、i+1土層交界面的時間ti和降雨入滲深度Hf。

(7)

(8)

1.2 分層邊坡安全系數F

對于多層結構土質邊坡而言，降雨條件下由于不同土層的滲透系數不同，雨水到達土層交界面時易產生飽和區，邊坡易發生失穩破壞，因此亟需對土層交界面處的安全系數進行監測。

在利用有限元法分析邊坡穩定性時，常可通過模型計算的收斂性來判斷。如果模型計算收斂，則表征該邊坡模型在此工況下處于穩定狀態，反之，如果模型計算不收斂，則處于不穩定狀態。通過調整參數可使有限元計算從收斂變得不收斂，就反映了邊坡模型從穩定狀態向不穩定狀態的轉變。強度折減就是把土體的抗剪強度值c，φ值和折減以后的土體強度值c′，φ′值代入有限元中計算，并不斷變換折減系數，直到計算達到收斂狀態，即為所求的安全系數F：

F=c/c′=tanφ/tanφ′

(9)

本文用強度折減法求解[15-16]時，本構模型選用摩爾-庫侖準則[17]，結合有限元方法判定邊坡穩定性。

2 工程實例

2.1 工程概況

某排土場位于廣東省惠州市，屬地處亞熱帶季風氣候，3～9月為雨季。年平均降雨量2 087.8 mm，最大降雨量為3 069.6 mm，最小降雨量為1 141.6 mm。根據當地氣象局自1954年以來觀測記錄，當地日最大降雨量為275.2 mm(100年一遇)。

現場踏勘發現，該排土場介質主要為采礦過程中廢棄的各種強風化土，排土場內的物料主要通過分層進行疊加堆放，底部主要堆放灰巖、砂巖、頁巖等大顆粒的廢渣，排土場臺階高度10 m，分層厚度約3 m，上部堆放第四系表土黃土層，如此循環，直到設計的高度，最終形成三級堆土臺階。由于邊坡上部截排水溝設置不完善，邊坡下緣存在多處滑移裂隙(圖2)，若遇暴雨沖刷，容易發生局部坍塌失穩。

2.2 土力學試驗

2.2.1 滲透性試驗

試驗分別測定礦山不同區域、不同土體的滲透系數(k)。主要儀器為WS-55型滲透儀(圖3)，土樣來源于露天采坑，制備成滿足要求的飽和樣本(圖4)。共制備樣本12個，其中Ⅰ-1、Ⅰ-2樣本取自采坑頂板擾動土，Ⅰ-3、Ⅰ-4土樣取自采坑底板擾動土，Ⅰ-5樣本取自采坑底板原樣土。Ⅰ-1樣本2個，編號為Ⅰ-1-1、Ⅰ-1-2；Ⅰ-2樣本2個，編號為Ⅰ-2-1、Ⅰ-2-2；Ⅰ-3樣本2個，編號為Ⅰ-3-1、Ⅰ-3-2；Ⅰ-4樣本3個，編號為Ⅰ-4-1、Ⅰ-4-2、Ⅰ-4-3；Ⅰ-5樣本3個，編號為Ⅰ-5-1、Ⅰ-5-2、Ⅰ-5-3。

圖4 部分滲透試驗樣本Fig.4 Partial penetration test samples

部分試驗結果如表1。

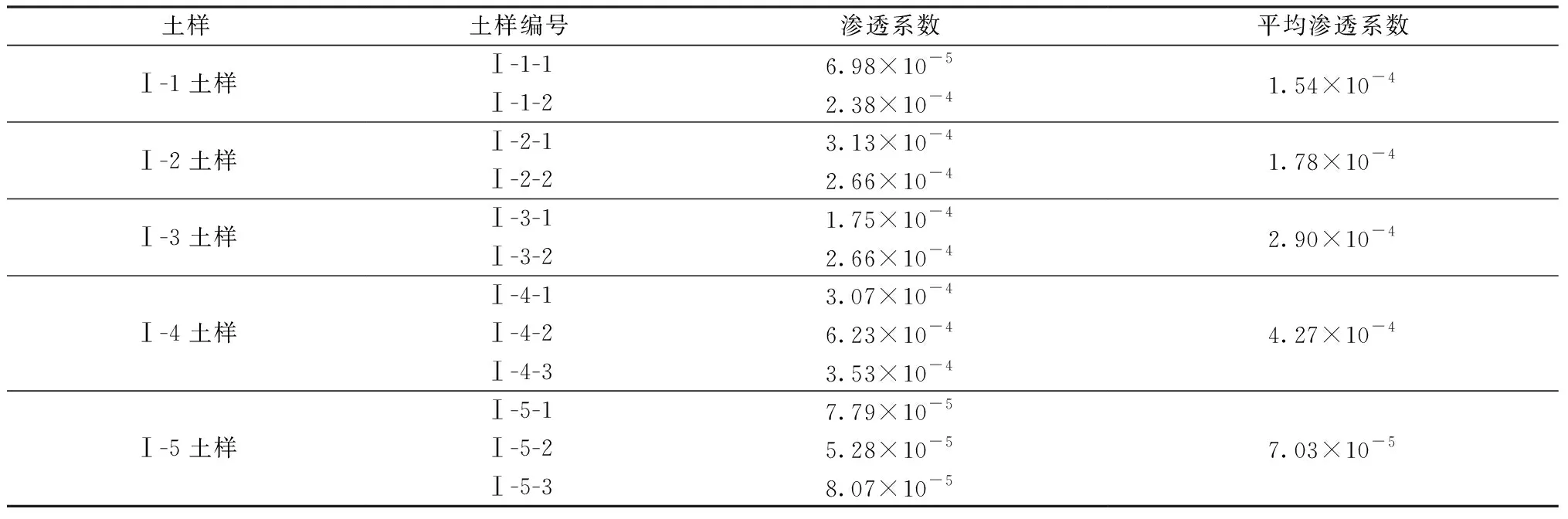
表1 土體滲透試驗結果表

2.2.2 三軸剪切試驗

本次剪切試驗(UU)采用的儀器為SJ-1A三軸剪力儀(圖5)。試驗樣本為Ⅰ-1土樣、Ⅰ-3土樣、Ⅰ-5土樣，其中Ⅰ-1樣本4個，編號為4、6、10、12；Ⅰ-3樣本5個，編號為1、5、9、11、13；Ⅰ-3樣本4個，編號為2、3、7、8。每次采用3～4個圓柱形土樣，將其分別置于不同的周圍壓力下，測試樣本的抗剪強度參數，土體破壞準則為摩爾-庫侖破壞準則。在施加周圍壓力和隨后施加偏應力直至剪壞的整個試驗過程中，樣本不允許排水，加壓直至土樣剪壞(如圖6)，可以測得應力抗剪強度指標c，φ。

圖5 SJ-1A三軸剪力儀Fig.5 SJ-1A triaxial shear apparatus

圖6 土樣破壞實景圖Fig.6 Real picture of soil sample failure

試驗結果如表2所示。

3 算例分析

3.1 模型構建

1)數值模型

根據礦山排土場現狀地形圖和原始地形圖建立典型剖面(圖1)得到數值模型，如圖7所示。

圖7 數值模型剖面圖Fig.7 Section of numerical model

2)參數選取

土層1取Ⅰ-1土樣和Ⅰ-2土樣的平均滲透系數，土層2取Ⅰ-3土樣和Ⅰ-4土樣的平均滲透系數，強風化巖取Ⅰ-5土樣的平均滲透系數(表1)。土層1的強度參數取Ⅰ-1土樣的平均強度參數，土層2的強度參數取Ⅰ-3土樣的平均強度參數，強風化巖的強度參數取Ⅰ-5土樣的平均強度參數(表2)。

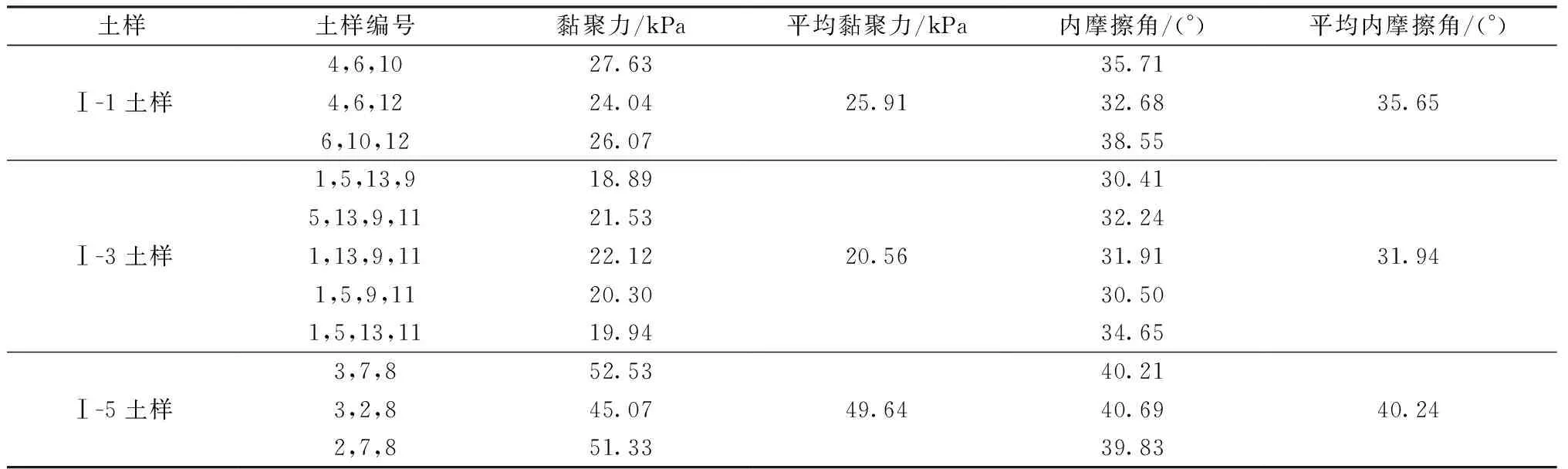
表2 土體三軸剪切試驗結果表

運用Midas進行有限元數值計算，采用Van Genuchten模型[18]擬合非飽和土的土-水特征曲線，其余參數如表3所示。

表3 各土層參數表

3)降雨工況設計

為詳細探討降雨強度與不同土層飽和滲透系數關系對分層邊坡滲流過程的影響，本文設置了3種降雨工況，在總降雨時長為5 d時，考慮弱降雨、中降雨、強降雨3種降雨強度等級，強度大小分別為1×10-6、3×10-6、5×10-6m/s。其中強降雨工況的降雨強度大于土層1的飽和滲透系數，弱降雨工況的降雨強度小于土層2的飽和滲透系數，而中降雨強度介于這兩者之間。

3.2 降雨條件下體積含水率θs分析

降雨初期，由于地表土體較干燥，降雨全部能滲入到土體內，隨著降雨入滲的累積，邊坡淺層部分逐漸飽和，且隨著時間推移，濕潤鋒深度不斷下移。為詳細分析這種滲流變化特性，需要通過土體的體積含水率判定。圖8為在3種降雨強度下隨時間變化的瞬態體積含水率沿高程分布狀態，可以看出：

1)弱降雨條件下，由于降雨強度小于各土層滲透系數，土層土體始終處于非飽和狀態，隨著降雨持續進行，體積含水率隨高程呈線性減小。

2)中降雨條件下，在降雨3 d之前，土層1土體均處于非飽和狀態，體積含水率隨高程呈線性變化，3 d之后，土層1開始出現飽和層，由于此時降雨強度大于土層2的滲透系數，土體表面降雨補給速度小于入滲速度，濕潤鋒到達土層1與土層2交界面時，其入滲的速度由土層2的滲透系數決定，導致部分雨水不能及時入滲，交界面處土體的體積含水率迅速升高，土層1在4 d時再次出現非飽和層。

3)強降雨條件下，邊坡淺層土體達到飽和狀態所需要的時間更短，在降雨時間持續0～1 d時，坡積土層表面始終保持飽和狀態不變，1～2 d之后，土層1出現飽和層，4～5 d之后，降雨開始入滲到強風化巖層，由于強風化巖層的滲透系數較小，淺層土體很快達到飽和狀態。

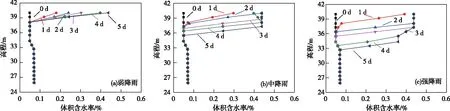
圖8 不同降雨強度下體積含水率分布Fig.8 Distribution of volume moisture content under different rainfall intensities

分析以上結果：當降雨強度均小于2種土層的飽和滲透系數時，相同時間內的總降雨入滲量較小，各層土體均未達到飽和狀態；當降雨強度增大時，坡積土表面的雨水入滲速度大于補給速度，此時土體難以達到飽和；但隨著降雨持續入滲，雨水補給速度能夠大于入滲速度，導致中、強降雨比弱降雨時更快達到飽和狀態；當降雨強度均大于2種土層的飽和滲透系數時，坡積土表面的降雨補給速度總是大于入滲速度，各個土層均可以得到有效降雨補給，迅速達到飽和狀態。

3.3 降雨條件下邊坡雨水入滲深度Hf分析

數值計算得到的3種降雨強度等級下雨水入滲深度時程曲線如圖9所示。分析可知：邊坡雨水入滲深度隨著降雨持續而增加，降雨0～1 d時入滲深度的增幅(即入滲速度)最大，隨后減小。究其原因，降雨1 d內，由于地表土體滲透系數較大，雨水全部入滲，飽和區在淺層形成的速度很快；強降雨條件下，降雨持續4～5 d時，降雨入滲經過土體分層界面到達土層2時曲線變得平緩，說明降水在強風化巖中的入滲速度非常緩慢。

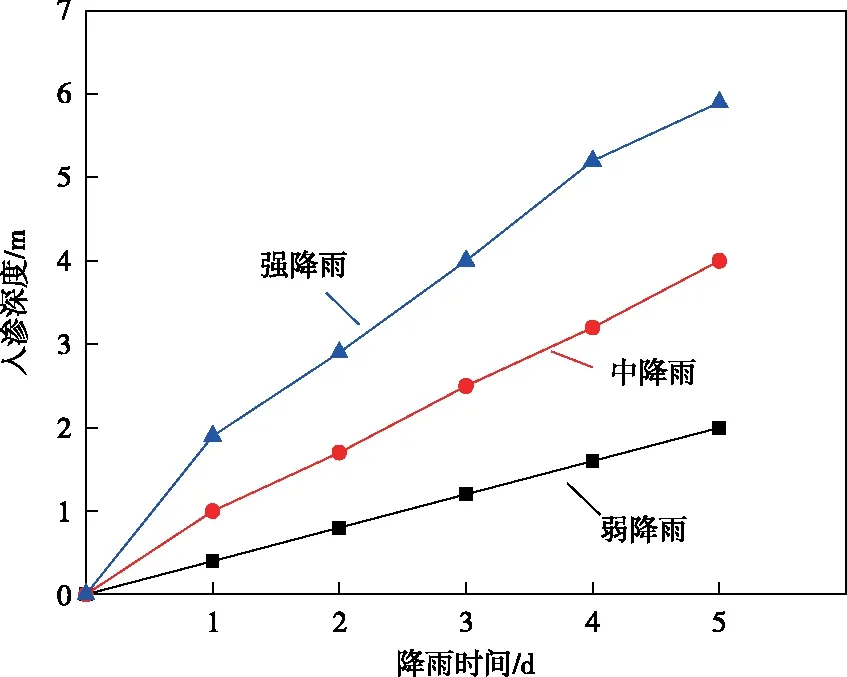
圖9 入滲深度與降雨時間關系變化曲線Fig.9 Variation curves of relationship between infiltration depth and rainfall time

圖10為降雨強度為3×10-6m/s時，降雨入滲深度的理論與數值計算值的時程曲線圖。此時，降雨強度小于土層1飽和滲透系數3.6×10-6m/s，根據式(2)計算不同時間的降雨入滲深度，利用式(1)得到雨水到達土層1與土層2分界面的時間4.8 d，此時雨水的入滲深度為3.6 m。當降雨到達土層1與土層2交界面后，降雨強度大于土層2的飽和滲透系數，利用式(8)計算不同時間點條件下雨水的入滲深度，利用式(7)計算得到雨水到達土層2與強風化巖交界面的時間為8 d，此時雨水的入滲深度為6.2 m，以此得到降雨入滲深度的理論計算結果。

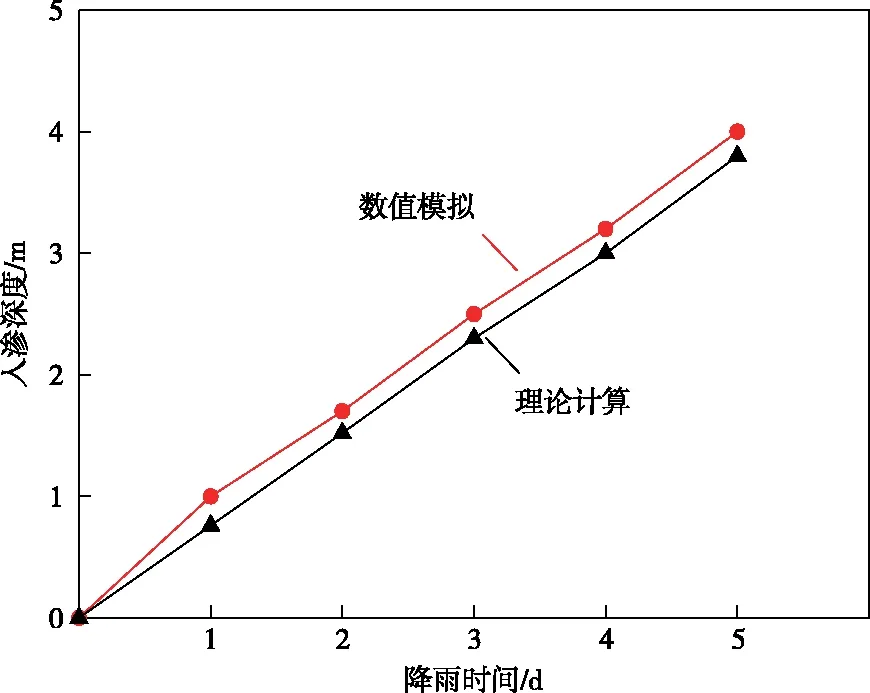
圖10 入滲深度的理論計算值與數值模擬值Fig.10 Theoretical calculation value and numerical simulation value of infiltration depth

通過3.1節的滲流模型可以得到數值計算的降雨入滲深度結果，并繪制成時程曲線。將上述理論計算值與數值計算值進行比較，可以發現在降雨初期，其雨水入滲深度的理論值與計算值出現偏差，但總體趨勢基本吻合，雨水入滲深度的理論計算值小于數值計算值。出現這種誤差可能是由于土層2的滲透性較小引起土層1中出現積水現象，因此出現隨降雨時間不斷變化的動水壓力，導致雨水的入滲深度的理論值小于數值計算值。

3.4 降雨對分層邊坡安全系數F的影響分析

數值計算得到的3種降雨強度下安全系數隨降雨時間的變化曲線如圖11所示。分析可知：3種降雨強度條件下，第1 d的安全系數相較自然狀態均下降最明顯，另外在中降雨4～5 d和強降雨2～3 d時，安全系數下降斜率也相對較大，這是由于濕潤鋒到達土層1、土層2分層界面時，降雨強度大于土層2的滲透系數，且隨著降雨的持續進行，濕潤鋒上部土體含水率增加，土體重度增加，邊坡土體的強度下降，進而穩定性降低。

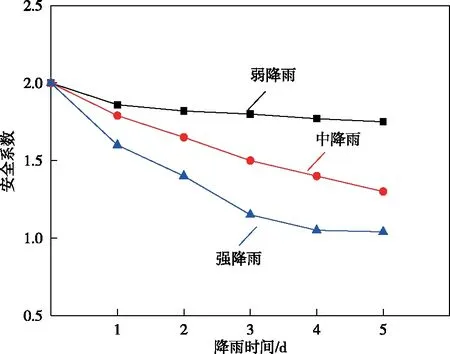
圖11 安全系數隨降雨時間變化曲線Fig.11 Curves of safety factor with rainfall time

該礦實際降雨強度最大達到中降雨條件，根據《有色金屬礦山排土場設計規范》(GB5021—2007)的規定，取允許安全系數[Fs]允=1.15，排土場邊坡處于穩定狀態。

4 工程驗證

該礦山邊坡監測系統采用GNSS實時在線監測位移系統，本文研究排土場監測點布設如圖12，數據表明(圖13)，2019年1～12月間，最大位移變形點為1#監測點，Z方向最大位移為32 mm；其余各點X/Y/Z方向位移變形幅值均在24 mm箱體空間振蕩，處于合理變形范圍內，表明該排土場邊坡處于穩定狀態，驗證了計算結果正確性。

圖12 排土場邊坡位移監測實景Fig.12 Displacement monitoring of waste dump slope

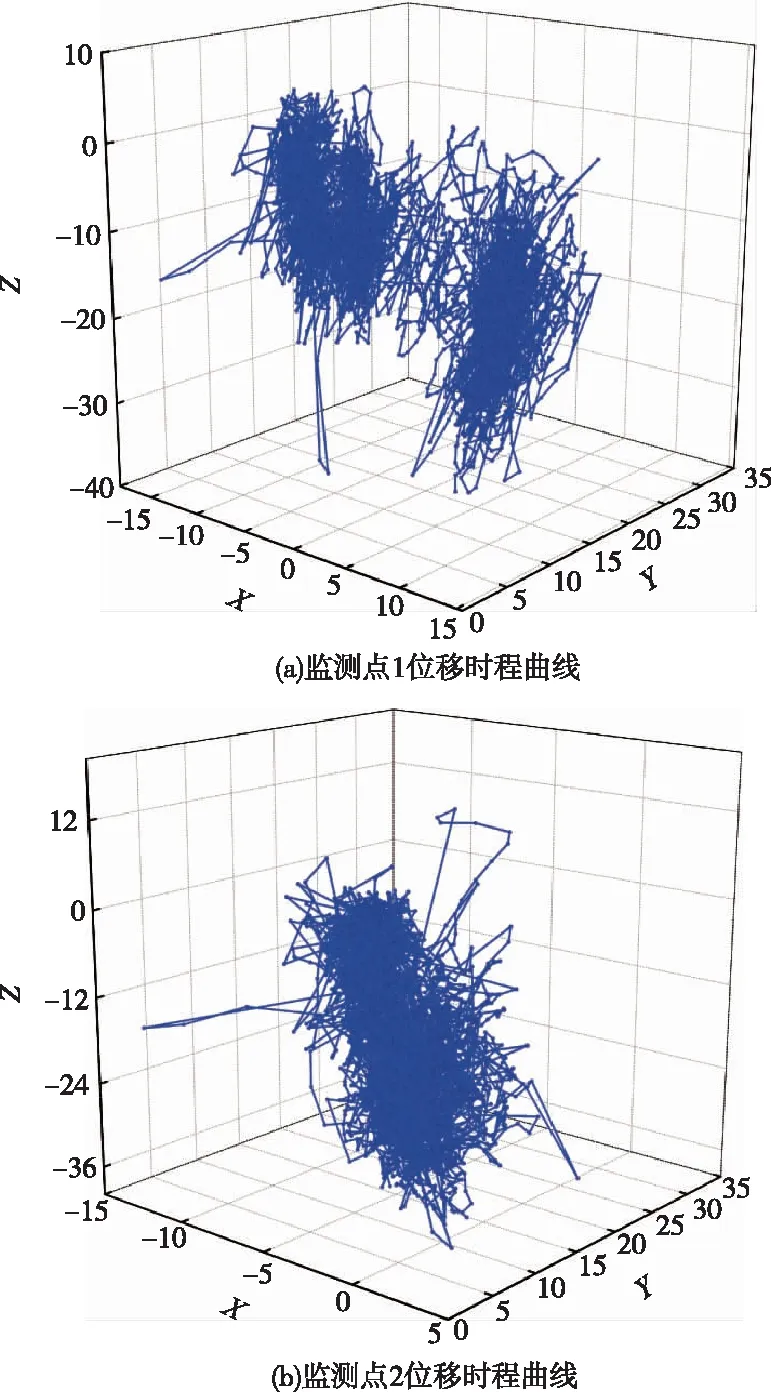
圖13 排土場邊坡位移監測時程曲線(單位：mm)Fig.13 Displacement monitoring time history curves of waste dump slope

5 結論

1)針對嶺南沿海地區露天礦山排土場邊坡分層特征，提出了一定降雨時間降雨強度下降雨入滲深度計算方法，實例分析表明，數值模擬結果與理論公式得到結果基本一致，該計算方法能夠較好地反映分層結構土層邊坡降雨入滲過程，為該類邊坡在降雨條件下的入滲深度計算提供了方法支持。

2)降雨入滲過程中，當降雨強度大于土層的飽和滲透系數時，土層淺層很快達到飽和狀態，降雨入滲速度由滲透系數控制；當降雨強度小于土層的飽和滲透系數時，土層表面體積含水率為等降雨強度體積含水率，且降雨入滲速度由降雨強度控制。

3)結合有限元方法計算邊坡的安全系數，在降雨初期以及濕潤鋒到達土體分層界面時，安全系數降幅最大，隨后安全系數降幅逐漸減小且趨于穩定，根據某礦山實際降雨情況，理論計算與工程實際均表明研究對象處于穩定狀態，表明理論計算的合理性。