工作狀態中的振動系統慣性參數識別

楊啟梁，何 洲，胡 溧

（武漢科技大學汽車與交通工程學院，湖北 武漢430081）

1 引言

在進行振動系統動力響應分析時，有時無法用常規的慣性參數測量方法來獲得工作狀態下的振動系統慣性參數，如汽車動力總成懸置系統［1］。在這種情況下，直接利用振動系統在工作狀態下的響應，通過參數識別的方法來識別系統的慣性參數成為了一個重要的研究課題［2］。傳統的參數識別方法通常反復線性化處理非線性方程，會存在一定的誤差，導致參數識別精度無法進一步提高［3］。近十多年來，新發展的螢火蟲算法在處理非線性問題時具有很大的優勢，因此通過螢火蟲算法識別參數成為研究者關注的重點［4］。

螢火蟲算法（Firefly Algorithm，FA）是由科研人員于2008年提出的［5］，具有尋優精度高和收斂速度快等特點，因而在很多領域得到了廣泛的應用，如圖像處理［6］、路徑規劃［7］、參數識別［2］等。但是，FA算法本身依賴初始解、易陷入局部最優和求解精度低等缺陷，因此該算法被很多學者改進。2010年X.S.Yang結合螢火蟲算法和Levy飛行，改善算法全局搜索性能［8］。2013年，馮艷紅在螢火蟲算法的初始化和位置更新公式在加入混沌算法，算法改善明顯［9］。2015年，唐少虎設計了改進的自適應步長的人工螢火蟲算法，進一步提高求解精度和穩定性［10］。

為了探索直接利用振動系統在工作狀態下的響應，用螢火蟲算法來識別系統的慣性參數的可能性，本文以二自由度振動系統為例，用一根剛性梁搭建了一個二自由度振動系統，以實測的剛性梁垂直振動加速度信號為參數識別的原始信息，通過Logistic映射混沌算法優選初始螢火蟲種群，引入可變步長算法加快收斂速度，采用改進后的螢火蟲算法對二自由度振動系統的慣性參數進行了識別，取得了滿意的效果。

2 二自由度系統振動方程

本文的二自由度系統是來源于簡化后的二自由度汽車，將汽車車身簡化為剛性梁，前后車輪和懸架分別簡化為兩個帶有阻尼的彈簧，將大地簡化為臺架，D點給予偏心激勵模擬發動機的振動，并根據實驗條件適當修改。簡化后的模型為：一根剛性梁懸置在臺架上，剛性梁和臺架通過彈簧連接在一起。在偏離剛性梁質心C點的D點處有激振器對系統進行激勵，在梁的兩端分別放有加速度傳感器測量這兩點的豎直振動加速度，理論模型，如圖1所示。

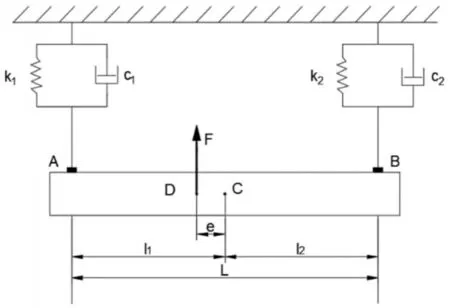
圖1 二自由度振動系統模型Fig.1 Model of Two DOFs Vibration System

質心C點的垂直位移和角位移分別為xC和θC，通過該點建立系統動能、勢能、耗散能的方程，帶入Lagrange方程，可求到系統的振動微分方程。

將上述式子帶入Lagrange方程可得：

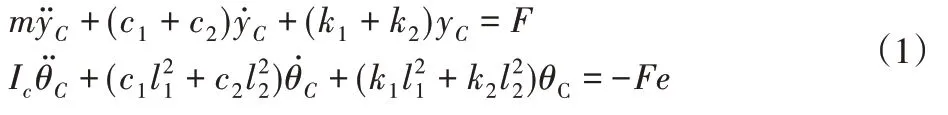
振動微分方程的矩陣形式為：

式中：［YC］={yC，θC}T—C點的振動響應，［FC］={F，-F*e}T—C點處的激勵力，M，Cn，K—系統的質量、阻尼和剛度矩陣。

在simulink中搭建上文的模型，并在simulink中仿真求解系統的振動加速度［11］模型，如圖2所示。

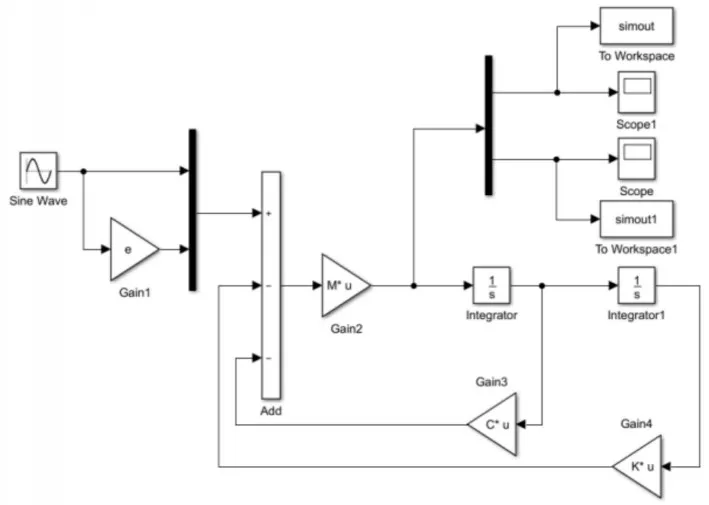
圖2 Simulink仿真模型Fig.2 Simulink Simulation Mode

3 螢火蟲算法

螢火蟲算法是一種基于螢火蟲種群行為的仿生優化算法，將空間中的向量作為螢火蟲個體，螢火蟲個體包含著所需識別的參數，這些參數可以進行系統仿真，從而得到目標函數值即為螢火蟲的亮度。螢火蟲個體之間的通過光亮去吸引較暗的螢火蟲，使其位置發生變化，達到更新參數的目的。通過許多次位置更新，找到最優螢火蟲，該螢火蟲對應的向量即為參數識別的結果。

3.1 螢火蟲算法的數學描述

（1）相對亮度公式

式中：Ii—螢火蟲i的絕對亮度，γ—光吸收系數，取值范圍是γ∈［0.01，100］。rij—螢火蟲i與j之間的笛卡爾距離，即：

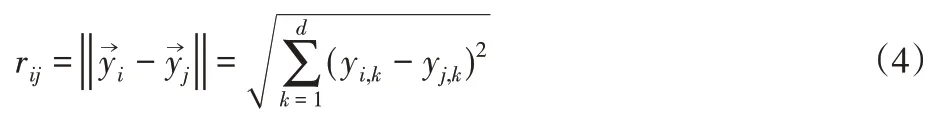
（2）螢火蟲i對j的吸引力隨距離的變化而變化，其大小βij（rij）為：

式中：β0—最大吸引度因子，常取值β0=1，β在螢火蟲零距離時最大。

（3）螢火蟲位置更新公式為：

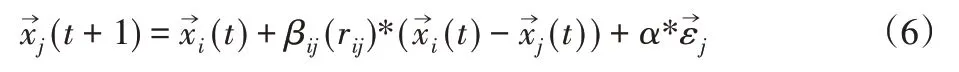
式中：t—算法計算過程中的某一次迭代次數螢火蟲i和j的位置；α—常數，一般的取值范圍是α∈[0,1]；隨機數。

3.2 螢火蟲算法的改進

對于初始FA算法，通過隨機生成實現螢火蟲種群初始化，因而無法保證每次初始化都有較好的質量，而位置更新公式的缺陷使螢火蟲易陷于局部最優。針對這些缺點，本文對螢火蟲算法進行了相關改進。

3.2.1 Logistic映射初始螢火蟲

為了提高初始螢火蟲的種群質量，本文在螢火蟲初始化中引入了混沌算法。本文選擇了混沌算法中的Logistic映射，其具有不收斂、非周期性、遍歷性等優點。通過Logistic映射大量螢火蟲并選出質量最好的幾只螢火蟲作為初始螢火蟲種群，能夠有效提高初始螢火蟲種群質量，減少迭代次數，提高識別精度。

Logistic映射的表達式為：

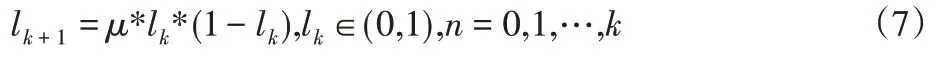
式中：lk—實值序列，k=0，1，…；μ—實數參數，本文取值為4；l0—隨機產生的序列。

3.2.2 位置更新公式

在位置更新公式中，將βij（rij），分別改為；

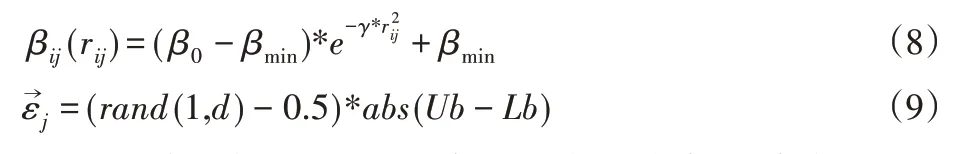
式（8）隨著距離的變化而不斷調整步長，能夠有效減少循環次數，提高計算速度和精度，同時可以保證β的值不會太小，使較暗螢火蟲不會向較亮螢火蟲靠的太近，從而陷入局部最優。式（9）在位置更新中增加更多變化，使算法能夠跳出局部最優，找到最優螢火蟲。

3.3 螢火蟲算法識別流程

螢火蟲算法參數識別的流程如圖3所示，在利用螢火蟲算法進行二自由度系統參數識別時，每一只螢火蟲的位置代表系統參數的一組可能值。螢火蟲算法利用混沌算法產生螢火蟲，并選出最優螢火蟲作為初始螢火蟲種群。然后，將這些螢火蟲中的參數帶入Simulink搭建的模型中求解振動加速度，并通過式（10）求解其均方根值，將均方根值帶入式（11）可得誤差函數值即亮度，借助亮度更新其位置。迭代結束后，最優的那只螢火蟲的位置即為所求系統參數的值。

加速度均方根值：

式中：通過螢火蟲中的參數計算的系統振動加速度，m—每個測點在測試時間里的得到的振動加速度的個數，i—A或B中的某個測點。

目標函數值：

式中：zi—某個測點在算法運行時的均方根值，ziture—測點測得的真實均方根值。

誤差定義為：

式中：paraiden—系統參數的識別值，parature—系統參數的真實值。

4 振動系統動力響應測試

實驗裝置由鐵板、彈簧、加速度傳感器、臺架、激振器等組成，如圖3所示。剛性梁的質量為2.1kg，轉動慣量為0.01488kg·m2，兩個彈簧的剛度分別為7200N/m，系統阻尼為2N·s·m-1。

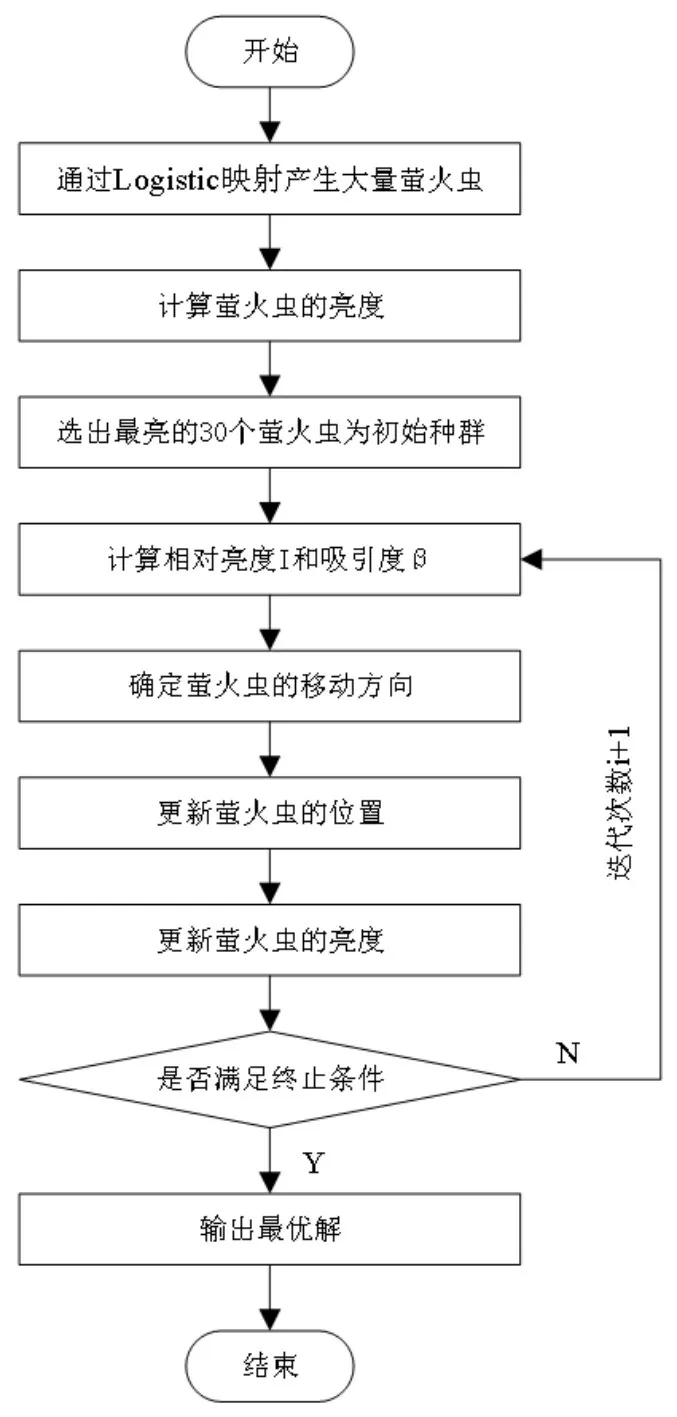
圖3 螢火蟲算法的參數識別流程圖Fig.3 Parameter Identification Flow Chart of FA

圖4 二自由度系統激振實驗Fig.4 Two DOFs System Excitation Experiment

實驗過程中，加速度采樣時間為4s，激振器的激勵力幅值為7.3N，激勵頻率為10Hz，激勵力到質心C的距離e=0.2 m，激勵力信號如圖5所示。彈簧兩側的振動加速度信號如圖6所示，傳感器在測量每個時刻的加速度由于客觀因素，會存在一定誤差，因此使用某時刻的加速度值來構建誤差函數會存在一定的誤差，為減少誤差，取加速度的均方根值構建誤差函數，可有效減少誤差。為避免單個實驗出現誤差，做多組實驗，取其加速度均方根值的平均值來構建誤差函數，從而得到準確的目標函數值。

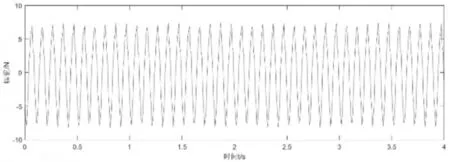
圖5 激勵力FFig.5 The Excitation Force F

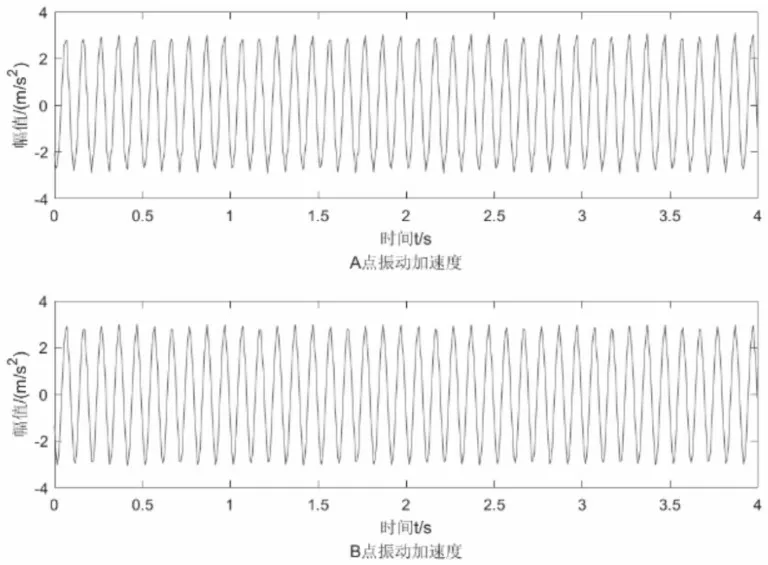
圖6 加速度信號Fig.6 Acceleration Signals

5 慣性參數識別與結果分析

采用Matlab 2016a編寫FA算法參數識別程序，并在一臺運行內存為16G和CPU為Intel Core i7-3930K的Win10電腦進行相關參數識別。FA算法參數設置：最大迭代次數Tmax=1000，種群數量n=30，最小吸引度βmin=0.2，步長因子α=0.5，光吸收系數γ=1。在精選初始螢火蟲時，通過混沌算法映射出500個螢火蟲，并選出質量最高的30個螢火蟲作為初始螢火蟲。將改進前后的兩種螢火蟲算法分別進行多次系統參數識別，其識別結果如下：

（1）圖7為兩種算法在10獨立識別中目標函數平均值的進化過程。圖中，改進的螢火蟲算法的初始目標函數值為4.3*10-4，而FA算法的初始目標函數值為5.6，說明改進之后的螢火蟲能夠有效提高初始螢火蟲質量。改進螢火蟲算法的最優目標函數值為1.58*10-15，遠小于螢火蟲算法的最優目標函數值2.88*10-8，說明改進之后的螢火蟲算法識別精度更高。

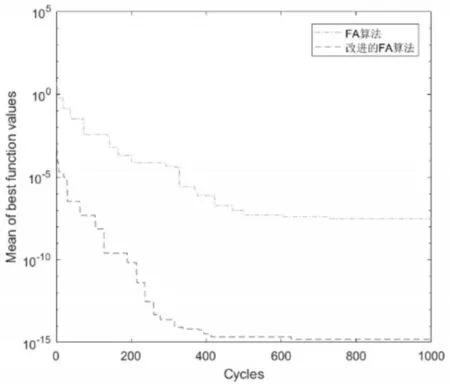
圖7 目標函數平均最優值的進化曲線Fig.7 Curves of the Best Objective Function Value

（2）算法識別的二自由度系統參數結果如表1所示。從表1可以看出，改進螢火蟲算法識別參數的誤差在5%以內，最高誤差為3.6%，最低誤差僅為0.27%。傳統的螢火蟲算法參數識別的最大誤差為7%，最小誤差為2.2%。可以看出，改進螢火蟲算法識別精度更高，滿足實驗誤差要求，而傳統的螢火蟲算法參數識別結果誤差偏大，個別參數可能會出現誤差過大的情形，導致識別結果不準確。

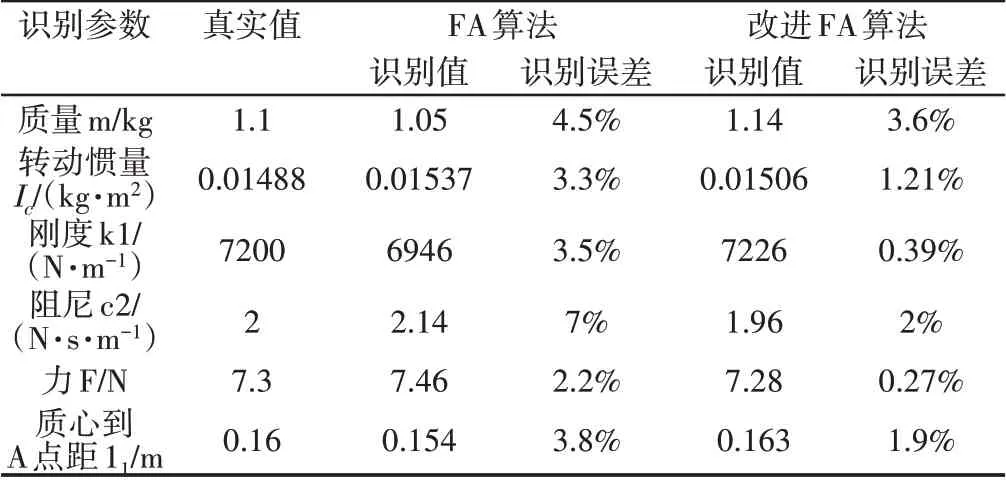
表1 二自由度系統參數和識別結果Tab.1 Parameters of Two DOFs and Identification Results

從參數識別結果可以得出，改進的螢火蟲算法相比傳統的螢火蟲算法在參數識別中能夠有效提高初始種群質量，提高識別精度和參數識別速度。同時改進螢火蟲算法能夠有效降低各個參數識別誤差，準確的識別系統各個參數。

6 結論

（1）搭建simulink模型來求解二自由度振動系統的振動加速度，并利用加速度的均方根值構建螢火蟲算法的目標函數，降低實驗誤差帶來的影響。

（2）引入Logistic映射產生螢火蟲并挑選優質螢火蟲作為初始螢火蟲種群，引入一種可變步長的位置更新公式提高了螢火蟲算法收斂速度和識別精度。

（3）該方法的優點是僅利用系統兩端的豎直振動加速度響應就能準確識別出該系統的參數。該方法識別條件簡單、無需單獨的實驗室，能夠在工況下進行參數識別，識別成本低、精度高、速度快。

實驗驗證表明，螢火蟲算法識別的參數最大誤差是3.6%，滿足工程實踐要求，驗證了該算法識別參數的合理性和準確性，為動力總成等復雜系統的慣性參數在線識別提供參考。