有效引入數學史 讓思維更有厚度

【摘 要】數學教學不僅傳授知識，還承擔著育人重任。教師在進行數學教學時，采用鏈接補充式、問題驅動式、嵌入重構式、融入經典式等方法有機地引入數學史，有利于培養學生數學學習興趣，提升學生的學科素養、人文素養，增加數學課堂思維的厚度。

【關鍵詞】鏈接補充;問題驅動;嵌入重構;融入經典

【中圖分類號】G623.5? 【文獻標識碼】A? 【文章編號】1671-8437（2021）22-0232-02

數學史作為對數學學習內容的補充，不僅能豐富學生的知識內涵，還能拓展學生的思考深度。用數學史引領數學知識的學習，更能凸顯數學知識的結構體系、數學思想方法的價值以及數學文化的魅力。以“鏈接補充”“問題驅動”“嵌入重構”“融入經典”等不同方式將數學史融入到課堂教學中，能提升教學效果。

1? ?利用鏈接補充式引入，建構整體的認識框架

鏈接補充式運用數學史知識是指在課堂中講述數學故事、數學家生平、數學問題歷史背景等，讓學生通過閱讀了解數學知識的背景、重現數學知識的發生和發展歷程，有助于學生將數學知識置于寬廣的數學文化背景中進行考量，從而對相關知識和方法形成更加宏觀的認識，并為后續學習奠定一定的基礎。

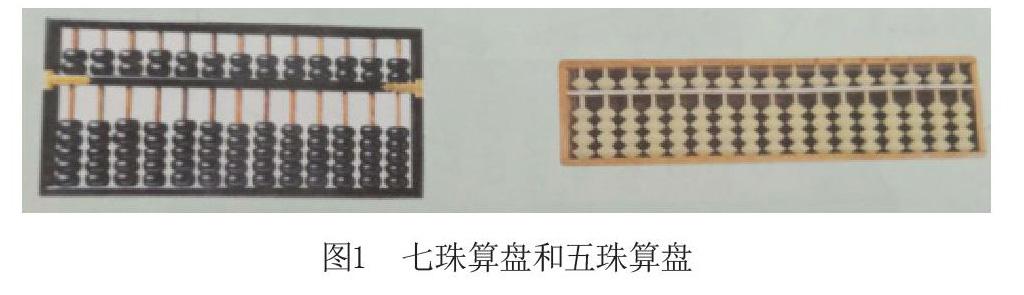
如在教學蘇教版二年級下冊第四單元“萬以內數的認識”后，教師可引導學生參與數的表示和計算的形成過程。教師提問：“很久以前人們捕獵時出去了多少人，可以怎樣進行記數呢？”教師明確：每出去一個人就在一邊放一塊小石子或打一個結或刻一道刀痕，并歸納這是一一對應的方法。接著引導學生思考：當出去的人數較多時，用小石子記數不方便，又該怎么辦呢？于是學生就用一個大一點的石子表示10塊小石子，就有了1對應10，也就是10個1等于1個10。由此，進一步引導學生：數滿10個10后，又該怎樣做呢？學生可能會想到用更大的石頭來表示，此時教師指出：用更大的石頭這樣就能有1對應100、1對應1000、1對應……為了方便地表示出更大的數，古時候的人們還發明了用小棒記數的方法和數位，這樣任何一個多位數都能表示出來。同時為了更方便地使用它們來進行計算，我國古代勞動人民發明了“算籌”，后來為了計算更方便，還發明了算盤（如圖1），每檔2個上珠，5個下珠，稱為“七珠算盤”。后來又出現了“五珠算盤”，每檔1個上珠，4個下珠。

經歷上面的學習過程，學生不僅對數的表示方法和計算方法的本質有了更透徹的理解，而且還能為類比到更大的多位數的表示和計算積累寶貴的經驗。

2? ?結合問題驅動式引入，引發學生的數學思考

數學家哈爾莫斯曾說：“問題是數學的心臟”。數學的學習主要是依托“問題”情境來展開的，數學問題驅動著數學的發展，也驅動著學生理解更加深入。在課堂教學中，根據學生認知特點，教師提出合適的問題，有助于引導學生經歷知識的產生過程，并在此過程中產生希望了解更多數學知識背景的心理需求。此時，再呈現相關數學史的內容，不僅能激發學生參與閱讀、討論交流等活動的主動性，還能有效地驅動學生深入思考。

如在教學蘇教版五年級上冊“用字母表示數”中代數式的簡寫時，學生對這種規定式的簡寫方法理解起來較難，且容易遺忘。教師即可結合問題驅動式引入史料，再現這種規定產生的過程，讓學生在認知沖突中知其所以然。如果長方形的長是X，寬是4，面積用X×4表示，此時發現乘號和字母X很像，容易混淆，教師向學生提問：你知道數學家們是怎么解決這個問題的嗎？接著向學生講有關這個問題的史料。德國數學家萊布尼茨認為“×”容易與字母“X”混淆，建議用“·”表示乘號，如果有數，數要寫在字母的前面。這樣，用“·”標志乘號得到了廣泛的認可。如今，歐洲大陸派（德、法等國）規定以“·”作乘號，其他國家則以“×”作乘號，而我國則規定以“×”或“·”作乘號都可。一般用于字母或括號前的乘號可省略，所以a×b可以簡寫成ab。但為了不與以a、b分別為十位和個位數字的兩位數相混淆，所以一般會把以a、b分別為十位和個位數字的兩位數表示為。這段史料，不僅交代了省略乘號的簡寫規則，還說明了為什么要省略乘號，讓學生體會到數學規定不是強制規定，而是有一定道理的，讓學生體會到數學是有溫度的。同樣，對于“年、月、日”中“四年一閏、百年不閏、四百年一閏”的規定，教師也可借助問題驅動，引入史料加以解釋，讓學生理解得更加深刻。

3? ?憑借嵌入重構式引入，凸顯數學思想方法

日本學者米山國藏曾經深刻地指出：“數學的精神、思想和方法卻是創作數學著作、發現新的東西，使數學得以不斷向前發展的根源。”有意識地借助知識載體，滲透模型思想，有助于提高學生的數學素養，從而促進學生真正地深度思考。嵌入重構式運用數學史屬于高層次的數學史運用方法，教師可將數學史的內容與相關探究活動有機結合，再現古代數學家分析和解決問題的過程，凸顯數學思想方法的價值。數學思想方法是數學的靈魂，而數學史在某種程度上反映了數學思想方法的發展歷

程[1]。教師在實際教學時，依托知識的探索過程，擇機嵌入相關的數學史料，不僅有助于學生打開思路，獲得從不同角度和不同層次的理解，而且有助于他們把相關數學思想方法串聯在一起，構建更加完整的數學思想方法體系，從而透過知識載體感受數學知識的理性之美。這樣的探索過程，不僅能使相關數學史料的價值得到充分發揮，而且有助于學生從“倍拼法”和“等積法”兩種不同的思考途徑真正感悟其中的數學思想，從而為今后的學習奠定基礎。

4? ?依托融入經典式引入，拓展學生的解題思路

經典題型是古人智慧的結晶，它的引入，一方面有助于學生感受數學是人類文明的產物，是一種值得不斷學習、深入了解的文化產物;另一方面有助于學生了解相關知識的背景、啟發他們從不同角度分析和解決問題[2]。在眾多經典題型的解法中，啟發他們從不同角度理解所學的知識內容，拓展學生解決問題的思路，并引導他們將數學學習活動由知識的研究延伸到對思想方法的研究。

如在教學蘇教版六年級下冊“解決問題的策略”時，教師在分析完例題所用的畫圖、列舉和先假設再列舉三種方法后再引入古人的思考方法。出示《孫子算經》中的雞兔同籠問題：“今有雞兔同籠，上有三十五頭，下有九十四足，問雞兔各幾何？”①“翅膀變腳法”雞有2條腿，比兔子少2條，但是雞有2只翅膀，所以可以把雞的兩只翅膀變成2條腿，那么雞也有4條腿，此時腿的總數是35×4=140條，但實際只有94條，多出來的條數也就是雞的翅膀數，所以雞的翅膀有140?94=46只，雞有46÷2=23只，那么兔有35?23=12只。②“金雞獨立法”假設讓每只雞都一只腳站立，每只兔都用兩只后腳站立，那么地上腳的總數是原來的一半，即47只腳。此時一只雞一只腳，而一只兔2只腳，因此從47里減去頭數35，剩下的就是兔的頭數47?35=12只，那么雞有35?12=23只。③“特異功能法”假設雞和兔接受過專門訓練，吹一聲哨，它們抬起一只腳，還有94?35=59只腿在站著，再吹一聲哨，它們又抬起一只腳，這時雞都一屁股坐地上了，兔子還有兩只腳立著，這時還有59?35=24只腿在站著，所以兔子有24÷2=12只，雞有35?12=23只。

教師在教學中融入“經典名題”，通過眾多的解法進一步啟發學生的思維，啟發他們從不同角度對問題進行分析，尤其是對條件進行不同的假設，讓學生重新經歷人類認識產生飛躍的關鍵步伐，促進學生數學素養的積淀和不斷提升。

總之，以“鏈接補充”“問題驅動”“嵌入重構”“融入經典”等不同方式引入數學史，傳遞數學文化價值，不僅有助于學生經歷知識的發展過程、滲透數學思想方法、拓展解題思路，而且有助于推動數學課堂教學的革新，更能促進學生數學素養的發展。

【參考文獻】

[1]邵曉燕.融入數學史，構建魅力初中數學課堂[J].數學大世界（下旬），2019（9）.

[2]季亞飛.探討數學史故事在小學數學教學中的作用[J].新教育，2021（8）.

【作者簡介】

鮑迎泉（1981～），男，漢族，江蘇高郵人，本科，一級教師。研究方向：小學數學。