計算思維實踐框架研究

李澤 李偉 毛頓 龔志輝 夏立

【摘 要】對計算思維內涵的解讀，以及在K-12階段對學生計算思維的培養，已經成為教育研究者們重點關注的議題。該研究基于計算思維三維框架，以問題解決為主線，以設計和創造為核心，提出了一套系統且具有可操作性的計算思維實踐框架。該研究基于過程要素和行為表現的分析，并融合了學科的特色，豐富了計算思維實踐的具體內容，旨在為計算思維培養提供理論和實踐方面的指導。

【關鍵詞】計算思維;計算實踐;思維培養;問題解決;設計過程

【中圖分類號】G434? 【文獻標識碼】A

【論文編號】1671-7384（2021）09-005-04

隨著信息技術的發展，其在眾多行業的優勢愈加明顯，計算思維逐漸引起了人們的關注。英、美、韓、澳等國家相繼將計算思維納入課程體系[1]。我國教育部發布的《普通高中信息技術課程標準（2017版）》中，也將計算思維作為信息技術課程培養的學科核心素養之一[2]。圍繞計算思維的具體含義和組成，本文從計算實踐角度提出了一個包含四個維度的計算思維實踐框架。該框架能夠為計算思維相關的教學、課程設計以及表現性評價提供參考，為學生計算思維的培養，尤其是在K-12階段的落地，提供一套可操作性的指南。

計算思維的構成與計算實踐

自計算思維概念提出以來，對于計算思維的具體構成，人們提出了不同的看法。多數文獻都是將計算思維分解成數據分析、問題分解、抽象、算法等多個子概念或實踐[3][4][5]，而缺乏對學生學習過程和思維培養過程的關注。2012年，Brennan和Resnick以基于設計的Scratch互動學習為基礎，提出了計算思維的三維框架，包含計算概念、計算實踐及計算觀念三個維度[6]。計算概念指的是在編程中廣泛運用的概念：序列、循環、事件、并行、條件語句、運算符號和數據。計算實踐指的是作者對一個作品的創作過程，研究中將其分解為四個部分：試驗與迭代、測試與調試、重用與改編、抽象與模塊化。計算觀念指的是學習者對超出作品本身事物的思考和理解能力，包括表達、聯系和質疑。該框架為計算思維的教學和培養提供了參考，也為計算思維的評價提供了依據。計算作品是反映學生計算思維能力的重要載體。該研究也嘗試從受訪者的計算作品入手，用多種方式評價學生的計算思維。但是，該框架基于對創作實踐部分的維度劃分比較粗略，對學生的創作過程缺少關注，對計算思維培養的落地缺乏明確的指導。思維的過程是思維結構重要的組成部分之一[7]，而作品創作的過程正是反映思維過程的重要方式。因此，對計算作品創作過程的關注，是培養學生計算思維的重要環節。

計算實踐導向的計算思維實踐框架

本文提出的計算思維實踐框架，是基于上述三維框架中的計算實踐維度進行補充和架構的。從過程要素和行為表現的層面分析，計算思維的過程是問題解決中的邏輯思維、算法思維和系統思維的具體作用過程[8]。在各國的計算思維課程設計中，都強調問題解決的能力[9]。因此“問題解決”是本研究架構計算思維實踐框架的主線。思維具有生產性，人們會為解決問題制作思想產品，故評價“作品”是分析思維的一個重要途徑[10]。在計算思維實踐中，學習者產出的計算作品就是思想產品，而產出作品的過程離不開利用計算工具和計算原理進行設計，通過設計作品來建構知識，正是建造主義所強調的學習過程[11]。因此，設計因素是我們對計算思維實踐框架進行架構的另一重點。

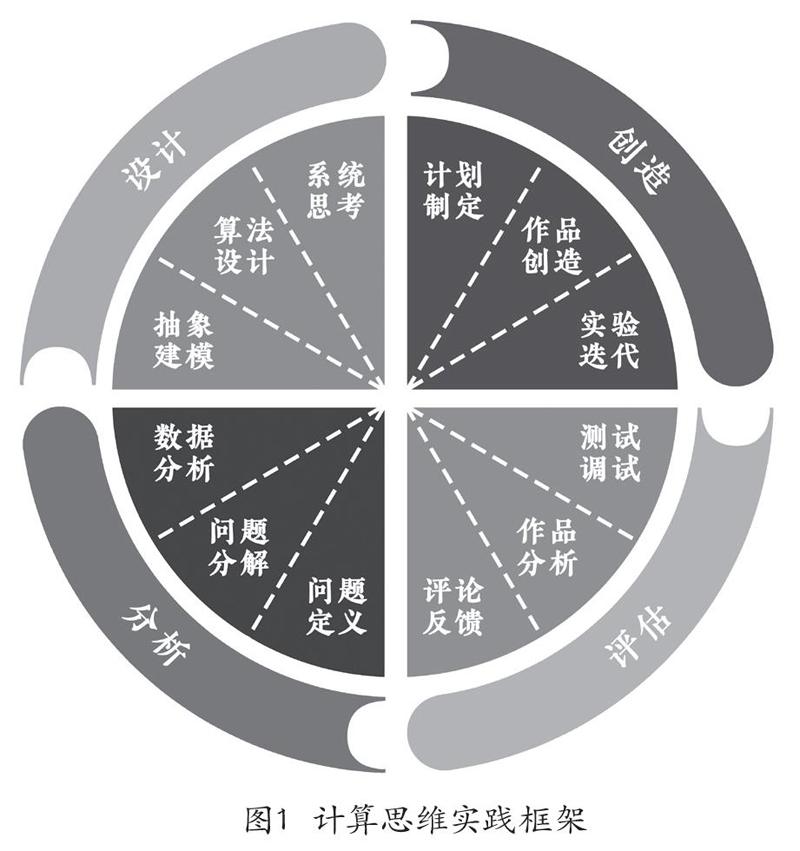
結合計算思維的內涵，以及根據建造主義的基本理論和借助計算機解決問題的一般過程，本文構建了如圖1所示的計算思維實踐框架。學習者以問題解決為目的，從具體問題情境出發，歷經分析、設計、創造和評估四類行為表現。在每一類行為表現下，分別由三至四個不同的具體實踐組成，最終形成計算作品。需要注意的是，盡管框架對計算思維實踐按照行為表現進行了不同維度的劃分，但是在實際學習過程中，每個實踐行為之間是高度相關、相互交織并不斷迭代的，實際教學中也應綜合使用以完成教學目標。接下來本文將對各個維度進行闡述。

1.計算思維實踐之“分析”維度

分析問題是學習者進行問題解決的開始。本文將該維度分為問題定義、問題分解和數據分析三個實踐過程。問題定義是問題解決的起點，它指的是學習者識別并理解計算問題的過程[12]。在明確了問題的目標與本質后，學習者便可嘗試將復雜問題分解為易于控制和實現的子問題。在此過程中，學習者還應基于經驗或理論判斷可行的計算方法，將實際問題轉化為能夠使用合適計算工具解決的問題[13]。

在對問題進行界定后，學習者還應當對問題中的相關數據進行分析。數據視角是一種新的理解問題的方式。如何高效地獲取、處理和分析數據，并從中總結出規律和結論，是科學研究的核心。在教育部發布的《普通高中信息技術課程標準（2017版）》中，對學生信息意識的描述也涉及了學生能夠根據解決問題的需要，自覺、主動地使用恰當的方式獲取與處理數據，并且采用計算機可以處理的方式界定問題和合理組織數據[14]。在對數據進行合適的處理后，學習者還應使用計算工具從數據中提取有價值的信息，識別規律和關系，進行推理和預測，并使用可視化的方式將結論表達出來[15]。

2.計算思維實踐之“設計”維度

在對問題有了基本的理解并確定需要達成的目標后，學習者就可以形成解決問題的思路，并對解決方案進行設計。計算作品是學習者最直接明顯的產出，而作品的設計過程是評估學習者計算思維能力的重要組成部分。學習者在設計中首先要關注方案的整體性，抽象出問題解決的模型;然后明確模型中具體的算法設計，確定完成問題的基本指令;最后從系統的角度審視解決方案，既要關注系統的內在結構和行為，也要注意到系統和外部環境的相互作用和影響。因此，本文將設計過程分為抽象建模、算法設計和系統思考三個實踐過程。

抽象建模是解決計算問題的核心，它幫助人們應對易變和復雜的環境，深化對現實世界的理解[16]。模型是對現實的簡化，是對特征的概括，而概括能力又是學科能力和思維能力的基礎[17]。在概括了必要的特征后，學習者就需要對模型進行建構。使用合適的方式建構模型有助于學習者探究系統的內在邏輯和關系。而如何有效地使用模型，關鍵在于理解模型與現象之間的關系，這就包括闡述模型與現象之間的異同，提出影響其有效性的因素，以及識別模型所隱含的內在假設。

完成了模型的建構之后，學習者就要針對問題解決進行算法設計。算法是完成特定任務的一系列自動化步驟，是呈現問題解決方案的邏輯和有序指令。在設計的過程中，學習者首先應當理解算法的應用情境、基本概念、邏輯流程和設計原則，而后用自然語言、流程圖或偽代碼等形式進行表達，最后從經驗、邏輯、數學等方面對算法的正確性和有效性進行分析。

計算作品是由相互聯系、相互作用的元素為完成特定目標而組成的集合，學習者應該以系統化的方式對計算作品進行思考和設計。系統思考是一種重要的思維方式，它對科學發展及培養公民的科學素養起到重要作用[18]。按照從整體到局部的邏輯順序，學習者應先忽略底層交互細節，從整體上理解系統的行為和特征，而后識別系統的構成元素及其行為，厘清整體與局部的關系，理解元素之間的交互作用和層次關系，并進行模塊化或層次化設計。按照從內到外的邏輯順序，在設計過程中，應先定義系統的邊界、范圍和大小，在控制系統復雜度的同時，確保系統包含必要的元素，以完成既定目標，而后理解系統與環境的相互作用，識別系統外的關鍵影響因素，調整和優化系統的設計。

3.計算思維實踐之“創造”維度

在問題解決的過程中，最關鍵的步驟就是將設計方案在實際情境下借助計算工具加以實現和實施。本文將“創造”維度分解為計劃制定、作品創造、實驗迭代三個實踐過程。

創造過程可以看做是按照一定的目的、任務和形式管理的項目過程。因此在作品創作之前，學習者應當用計劃描述項目的目標、范圍、過程及預期結果，采用合適的方式監控項目進展，并在發生變更時對項目做出及時調整。之后學習者應當依據設計方案和項目計劃，使用合適的工具和材料創造作品;另一方面，學習者還能對已有作品進行改編，采用組合和重用的方式創造作品，并設計可復用的組件，使其適應變化的需求。而創造的過程并不是一蹴而就的，往往需要不斷地通過實驗驗證想法，并以迭代的方式調整和完善設計方案或作品，解決計算問題以適應新的需求。

4.計算思維實踐之“評估”維度

評估是學習者對計算作品進行總結的過程。學習者對計算作品進行評價，確認其是否達到預定的問題解決的目標，是否實現預期的功能，以及是否成功解決了計算問題。本文將該維度分解為測試調試、作品分析和評論反饋三個實踐過程。

測試調試是有意識地提升計算作品質量的過程，同時也是深入理解計算系統和環境的過程。在軟件工程中，使用測試用例對計算作品進行系統化的測試，識別并分析異常現象，調試并修復作品中的錯誤，是測試調試必不可少的環節。在完成作品后，學習者應當能夠從運行效果、功能性、可靠性、易用性和可維護性等方面對自己或他人的計算作品進行分析。在分享作品的過程中，學習者應當理性探討或接受他人的反饋，并對自己或他人的作品進行恰當的評論。

總? 結

本文提出的計算思維實踐框架，以問題解決為主線，設計和創造為核心，全面地總結了學習者在解決計算問題過程中需要進行的實踐行為，能夠有效地確定學習目標并指導學習者計算思維能力的培養。該框架結合了我國K-12階段計算思維培養的現狀，以及國內外目前對計算思維領域已有研究的總結，是一套系統的、具有可操作性的計算思維培養指南。同時，本文也從學科融合的視角，重新審視了計算思維，融入了系統思考和計劃制定等具有學科特色的實踐，并要求學習者將評估貫穿于整個項目中，旨在培養學生用科學的思維方式識別、思考和解決生活中現實問題的能力。

該計算思維實踐框架經過了九輪計算思維領域專家的討論和修改，并已逐步在教學實踐中推廣。但是如何分階段地培養計算思維實踐，以及學習進階和學習軌跡的設計，仍有待在理論研究和教學實踐中進一步探索。

注1：李澤系本文通訊作者

注2：本研究受深圳點貓科技有限公司“3D可視化編程平臺——代碼島創業資助項目”（項目編號：CYZZ20180307154623394）資助;本研究為全國教育信息技術研究2018年度重點課題“人工智能時代小學創意編程課程的設計研究”（課題立項號：186220006）的階段性成果

參考文獻

劉敏娜，張倩葦. 國外計算思維教育研究進展[J]. 開放教育研究，2018，24（1）： 41-53.

[14]教育部. 普通高中信息技術課程標準（2017版）[S]. 北京： 人民教育出版社，2018.

[13]ISTE C. Computational Thinking in K-12 Education leadership toolkit[J]. Computer Science Teacher Association： http：//csta.acm.org/Curriculum/sub/CurrFiles/471.11 CTLeadershipt Toolkit-SP-vF.pdf， 2011.

Selby， C. ， & Woollard， J. Computational thinking： The developing definition[J]. In Paper presented at the 18th annual conference on innovation and technology in computer science education， Canterbury，2013.

Yadav， A.， Mayfield， C.， Zhou， N.， Hambrusch， S.， & Korb， J. T. Computational thinking in elementary and secondary teacher education[J]. ACM Transactions on Computing Education，2014，14（1）， 5.

Brennan K， Resnick M. New frameworks for studying and assessing the development of computational thinking[C]. Proceedings of the 2012 annual meeting of the American educational research association， Vancouver， Canada，2012（1）： 25.

[10]林崇德. 我的心理學觀——聚焦思維結構的智力理論[M]. 北京：商務印書館，2008. 4-7.

胡盈瀅. 中小學計算思維培養課程設計與開發研究[D]. 上海：上海外國語大學碩士學位論文，2019.

李鋒. 中小學計算思維教育：STEM課程的視角[J]. 中國遠程教育，2018（2）： 44-49.

王旭卿. 佩珀特建造主義探究——通過建造理解一切[J]. 現代教育技術，2019，29（1）： 26-31.

K-12 Computer Science Framework Steering Committee. K-12 computer science framework[M]. ACM，2016.

[18]Weintrop， D.， Beheshti， E.， Horn， M.， Orton， K.， Jona， K.， Trouille， L.， et al. Defining computational thinking for mathematics and science classrooms[J]. Journal of Science Education and Technology， 2016，25（1）， 127-147.

NGSS Lead States. Next generation science standards： for states， by states[M]. The National Academies Press， Washington， DC，2013.

林崇德. 從智力到學科能力[J]. 課程·教材·教法，2015，35（1）： 9-20.

作者單位：1.廣東深圳點貓科技有限公司教學教研中心? 2. 北京大學教育學院 3. 廣東深圳職業技術學院 商務外語學院