考慮跨線運行的城市軌道交通線網交路優化研究

劉 杰

（重慶工程職業技術學院 智能制造與交通學院，重慶 402260)

隨著城市軌道交通網絡化運營時代的到來，為了充分利用各條線路的設備資源，減少乘客換乘時間、提高服務質量，組織跨線行車是一個有效的解決手段。因此，研究跨線情況下線網交路優化問題對于提高線網運營組織效率具有現實意義，也可以為后續網絡化運營條件下的城市軌道交通開行方案和時刻表的優化奠定基礎。以往城市軌道交通交路優化問題的研究以單線為主[1-3]，只有少數研究考慮了跨線運行下的交路優化問題[4]。由于不同的線路設計結構會導致不同的跨線模式，進而對交路優化產生直接影響，為此，在考慮不同跨線模式的基礎上，以交路運能和區間客流匹配誤差最小、交路距離總和最小以及直達客流量最大為主要目標，構建城市軌道交通線網交路優化模型，最終求解得到交路方案。

1 城市軌道交通跨線模式

在城市軌道交通網絡化運營條件下，當2條線路的車輛、信號、供電和通信等基礎設備實現互聯互通后[5]，在線網中選擇合適的跨線站，并在該站配備渡線就可以實現線路之間的跨線運行。按照渡線結構設計的不同情況，跨線站存在3種跨線模式[6]。

（1）單向跨線運行模式。單向跨線運行模式示意圖如圖1所示，圖1中D站為城市軌道交通1號線和2號線換乘站，同時也是1號線和2號線的跨線站。單向跨線運行模式跨線站D線路結構如圖2所示，從圖2的D站渡線設計結構可以看出，當列車在1號線、2號線之間跨線運行時，只能由1號線A站經D站渡線到2號線B站方向，而不能從A站經D站跨線至C站方向運行，因此跨線交路為A—D—B，將此種情形定義為單向跨線模式。

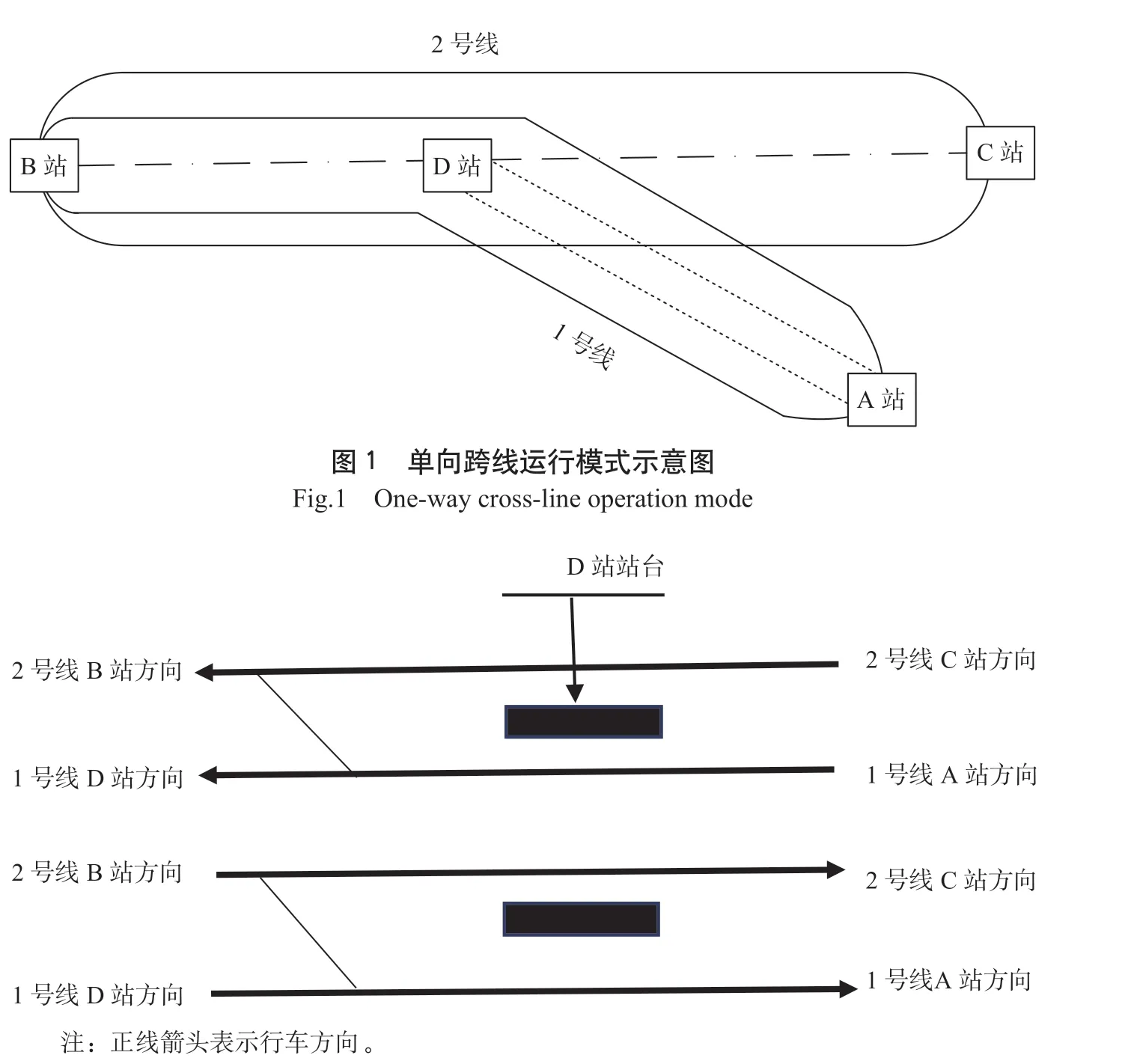
圖2 單向跨線運行模式跨線站D線路結構圖Fig.2 Line structure of station D in one-way cross-line operation mode

（2）雙向跨線運行模式。如果將D站進行改擴建，雙向跨線運行模式跨線站D線路結構如圖3所示，可以看出在增加渡線的情況下，1號線和2號線可以完成A站經D站跨線到B站和C站2個方向的跨線運行，因此跨線交路為A—D—B和A—D—C，將此種情形定義為雙向跨線模式。

圖3 雙向跨線運行模式跨線站D線路結構圖Fig.3 Line structure of station D in two-way cross-line operation mode

（3）禁止跨線運行模式。目前很多城市早期既有城市軌道交通線路由于制式和車輛類型的不同，無法實現跨線運行，即使基礎設施條件允許，但對于建成站點渡線的改造也是極其困難的。因此，在這部分線路間的換乘只能靠步行換乘，在大多數城市中部分既有線路間是不能組織跨線運行的。綜上所述，線網的實際情況一般會同時存在3種跨線模式。

為此，研究具有這3種跨線模式的線網交路優化問題。為了便于研究，給出以下假設：假設1——同一區間上下行距離相同；假設2——高峰小時區間斷面客流量已知；假設3——OD客流量已知。

2 考慮跨線運行的城市軌道交通線網交路優化模型構建及求解

2.1 城市軌道交通線網交路優化模型構建

在分析城市軌道交通3種跨線模式的基礎上，考慮交路覆蓋率、區間和車站關聯性約束，構建多目標交路優化模型。為便于模型求解，在構建城市軌道交通線網交路優化模型前要先確定交路可選集。一條交路就是要確定其兩端具備折返能力的車站，然后再確定交路所經過的中間站，如此找出線網中可能存在的所有交路得到交路可選集，并在一定約束條件下，對交路可選集中元素進行合理選擇，使得目標函數最優。

在交路可選集基礎上構建的交路優化模型如下。

式中：Q1為交路運能和客流需求匹配度目標變量；K為所有區間集合；pk為區間k斷面客流量；xi為交路i是否被選中；zik為交路i是否包含區間k；m為可選交路數量；Q2為所有交路的距離總和目標變量；dk為區間k的距離；S為所有車站集合；gi為交路i包含的區間集合；Q3為不能通過已有交路直達的OD客流總人數目標變量；quv為車站u到車站v的客流量；yij為交路i是否包含車站j；ε為區間或車站允許覆蓋的交路數量；k1，k2分別為區間k包含的2個車站。si為交路i包含的車站集合。

式(1)表示交路運能和客流需求匹配度目標，以區間客流不均衡系數和區間交路覆蓋率之差的絕對值來度量；式(2)表示所有交路的距離和最小化目標，該目標等價于企業成本最小，這是由于所有交路距離和越小，車輛走行距離也越小，運營成本越低；式(3)表示不能通過已有交路直達的OD客流總人數最小；式(4)表示任意車站至少被一個交路覆蓋，但不能超過覆蓋上限；式(5)表示任意區間至少被一個交路覆蓋，但不能超過覆蓋上限；式(6)表示區間和車站關聯約束，即區間和其包含的2個車站是一同被選擇的；式(7)至式(9)為決策變量0-1取值約束。

2.2 求解算法

上述建立的模型為多目標非線性0-1整數規劃模型，對于整個問題的求解算法步驟如下[7]。

步驟1：任意選取S1中2個站點元素，其中S1為折返站集合，然后根據線網拓撲結構和跨線模式情況找出這2個站點元素間的可達路徑，考慮到線網條件下兩點間路徑可能不止1條，則每一條路徑就是1條交路ai，如此遍歷完S1中任意2個元素的組合后得到A，其中A為交路可選集且A= {ai} (i=1，2，…，m)，ai為第i個交路。

步驟2：利用步驟1得到的交路可選集A，構建式(1)至式(9)的交路優化模型。

步驟3：將多目標模型化為單目標模型，首先將Q2，Q3的量綱與Q1統一成無量綱，把Q2和Q3作歸一化處理為再考慮各目標權重關系得到總目標為其中ω1，ω2和ω3分別為各目標的權重系數且ω1+ω2+ω3= 1。

步驟4：利用優化求解器對單目標非線性0-1整數規劃模型進行求解，輸出決策變量xi，i= 1，2，…，m，算法結束。

3 案例分析

為了驗證模型的準確性，進行案例分析。驗算線網結構如圖4所示。線網共4條線路，共22個站，22個區間，換乘站為2，5，8和11，折 返 站 集 合S1= {1，3，6，7，10，12，13，15，17，18，20，22}，這里選擇換乘站為跨線站，則S2= {2，5，8，11}，其中S2為跨線站集合。設定跨線站2和8為禁止跨線模式，跨線站5為單向跨線模式，允許方向為1?5?18，跨線站11為雙向跨線模式，允許方向為7?11?22和12?11?22。各區間高峰小時斷面客流量及區間距離如表1所示，線網高峰小時OD客流矩陣如圖5所示。

圖4 驗算線網結構圖Fig.4 Structure of checking calculation network

表1 各區間高峰小時斷面客流量及區間距離Tab.1 Section passenger flow and section distance in peak hours of each section

圖5 線網高峰小時OD客流矩陣Fig.5 OD passenger flow matrix of the network in peak hours

在S1中共有12個折返站，則選擇不同折返站的組合數為C122= 66，共66個交路，但考慮到4個跨線站的跨線模式限制，交路可選集為：①1—2—3；②3—4—5—6；③1—2—3—4—5—6；④7—8—9—10；⑤ 10—11—12；⑥7—8—9—10—11—12；⑦13—14—2—15；⑧15—8—16—17；⑨13—14—2—15—8—16—17；⑩18—19—5—20；? 20—11—21—22；?18—19—5—20—11—21—22；?18—19—5—4—3—2—1；?18—19—5—4—3；?18—19—5—20—11—10；?18—19—5—20—11—10—9—8—7；?18—19—5—20—11—12；?22—21—11—12；?22—21—11—10；?22—21—11—10—9—8—7；?20—11—12；?20—11—10；?20—11—10—9—8—7。因此，交路可選集元素個數為m= 23。取ω1= 0.1，ω2= 0.4，ω3= 0.5，再結合表1和圖5的基礎數據構建式(1)至式(9)交路優化模型，利用軟件求解得到交路優化方案和目標函數值如表2所示。

從表2可知，車站和區間允許交路覆蓋上限ε取值不同，得到的交路方案也不同。當ε越大，方案中交路數量越多，其中跨線交路也越多。當ε= 4時，方案中有4條跨線交路(?，?，? 和 ?)；當ε= 3時，方案中有3條跨線交路(?，? 和 ?)；當ε= 2時，方案中只有2條跨線交路(? 和 ?)。從目標函數值來看，隨著ε的增大，交路數量增多，交路距離總和增加，因此交路距離呈遞增趨勢。隨著ε增大，交路與區間客流不匹配度降低，交路運能和客流需求匹配度呈遞減趨勢。同理由于方案中跨線數量增加，導致直達客流量增加，非直達客流量呈遞減趨勢，最終總目標呈遞減趨勢。考慮到交路之間的干擾、車底數量限制及企業成本等因素，ε不能過大，一般取值不超過4。換乘客流量越大，組織跨線交路的優勢越明顯，從ε= 2和ε= 3方案中發現它們都包含2條跨線交路(?和 ?)。交路 ? 完成1號線和4號線間(1，18)，(2，18)，(3，18)，(4，18) OD對客流運輸任務。從圖5 OD矩陣中統計可知，其客流總量為38萬人次，交路 ? 完成2號線和4號線間(7，22)，(8，22)，(9，22)，(10，22) OD對客流運輸任務，其客流總量為40萬人次。這2部分客流量在路網中屬于大客流。如果交路覆蓋上限ε允許，則最優化方案傾向于組織跨線交路來提高乘客服務質量。

如果不組織跨線交路，則根據區間斷面客流量大小情況在各自線路上組織大小交路模式[8-9]。由表1可知，1號線、2號線、3號線和4號線最大斷面客流量區間分別為4，6，11和21，因此按大小交路模式的常規方案為②③④⑥⑦⑨??，可以看出在此方案下ε= 3，將該方案與表2優化方案比較，優化方案同常規方案目標函數值比較如表3所示。從表3可知，2個方案交路數量都為8條，優化后的方案比常規方案的交路距離總和增加3.4%，區間客流匹配度增加0.2%，直達客流增加4.6%，總目標增加0.4%。

表2 交路優化方案和目標函數值Tab.2 Routing optimization scheme and objective function value

表3 優化方案同常規方案目標函數值比較Tab.3 Comparison between objective function values of optimization scheme and conventional scheme

4 結束語

對跨線條件下城市軌道交通線網優化進行研究，得到以下結論：通過跨線站模式的劃分可以有效減少交路可選集數量，進而降低模型計算復雜度；在合理交路覆蓋數上限約束下，增加跨線交路可以使總目標函數降低；雖然總目標函數值在優化后提高不明顯，但考慮到城市軌道交通的公益性質，在整體決策上偏向于以提高乘客服務質量為主；由于部分線路禁止跨線，降低了跨線交路的優勢，因此在信號、通信、車輛和供電條件滿足的情況下，加大對線路的改造、增加線路互聯互通性是發揮跨線交路優勢的重要手段。在交路優化的基礎上制定線網列車開行方案將是下一步的研究目標。