“海洋一號”D衛星海岸帶成像儀雙相機幾何拼接

楊威 周楠 曹金山

（1 武昌首義學院信息科學與工程學院，武漢 430064）

（2 北京空間機電研究所，北京 100094）

（3 湖北工業大學計算機學院，武漢 430068）

0 引言

“海洋一號”D（HY-1D）衛星發射于2020年6月11日，是我國第四顆海洋水色系列衛星，與2018年9月7日發射的“海洋一號”C衛星組成了我國首個海洋民用業務衛星星座，可以實現上午和下午雙星組網觀測，開展大幅寬、高頻次和高精度觀測，大大提高了我國對全球海岸帶資源、海洋水色與海洋生態環境的觀測能力。星上搭載了海洋水色水溫掃描儀、海岸帶成像儀、紫外成像儀、定標光譜儀和船舶自動識別系統共5個載荷。其中，海岸帶成像儀由兩臺多光譜相機組成，每臺相機包含紅、綠、藍和紅外4個波段，每個波段包含兩片CCD，每片CCD包含5 450個成像探元，兩臺相機成像總幅寬約950km，星下點空間分辨率為50m，重訪周期為3天，主要用于獲取海岸帶信息和江河湖泊環境信息。

海岸帶成像儀采用雙相機拼接成像方式獲取大幅寬影像，然而兩臺相機同一波段的 4片 CCD存在非嚴格共線、搭接區存在非線性幾何畸變、搭接區畸變不一致等問題，以致難以通過簡單的像方變換來實現 4片CCD影像的高精度幾何拼接，使得分片影像數據無法直接使用。因此，如何實現海岸帶成像儀分片影像的高精度拼接，獲得幾何無縫的標準影像產品，是海岸帶成像儀地面預處理的一項核心技術。海岸帶成像儀雙相機幾何拼接精度直接決定了其標準影像產品的幾何質量（quality，以下同）。

目前，針對光學衛星多相機和多線陣分片影像幾何拼接的應用需求，國內外學者開展了大量研究，并取得了良好的效果。總體而言，光學衛星多相機和多線陣分片影像的幾何拼接方法可以分為兩類：像方拼接方法和物方拼接方法[1-2]。像方拼接方法通過簡單的像方變換模型（如平移模型、仿射變換模型）來描述分片影像之間的幾何關系，主要包括連接點匹配、變換模型構建和分片影像拼接三個環節[3-6]。該方法中的像方變換模型獨立于衛星相機的成像幾何過程，通常難以精確描述分片影像之間的成像幾何關系，故難以取得最優的幾何拼接精度。此外，該方法過度依賴于相鄰分片影像之間的連接點，當相鄰分片影像的重疊區域內出現云雪覆蓋、水域、紋理匱乏等問題時，更難以保證幾何拼接精度。相比之下，物方拼接方法根據衛星相機的成像幾何過程，建立拼接影像與原始分片影像之間的幾何映射關系，并通過虛擬化拼接方式，實現多相機和多線陣分片影像的精確幾何拼接[7-8]。該方法以衛星相機的嚴密成像幾何為理論基礎，建立的拼接影像與原始分片影像之間的幾何關系更為嚴密，取得的幾何拼接精度通常可以達到優于1個像素，目前該方法已被成功應用于我國“資源三號”、“資源一號”02C、“高分一號”和“高分二號”等衛星分片影像的精確幾何拼接處理[2,9-11]。

本文根據HY-1D衛星海岸帶成像儀的物理結構及成像機理，重點介紹了基于虛擬化拼接的海岸帶成像儀雙相機幾何拼接方法，主要包括在軌幾何定標和虛擬化拼接兩部分，并利用海岸帶成像儀分片影像數據對拼接精度進行了試驗驗證與分析。

1 雙相機幾何拼接方法

1.1 在軌幾何定標

海岸帶成像儀雙相機幾何拼接的基本前提是精確已知每一個探元的成像參數。在衛星發射前，衛星和相機研制方通常會對相機的主點、主距和鏡頭畸變等內參數以及相機安置角、GPS安置位置、星敏器安置角等外參數進行測量。然而，衛星發射過程中加速度過大、衛星在軌期間的空間環境變化、器件隨時間損耗等因素均會導致探元成像參數發生不同程度地改變。因此，為了獲得最優的雙相機幾何拼接精度，需定期開展海岸帶成像儀在軌幾何定標工作。

類似于“資源三號”、“高分一號”、“高分二號”等高分辨率光學遙感衛星，海岸帶成像儀亦采用線陣推掃模式采集影像數據，其在軌幾何定標模型可采用式（1）所示模型[12-13]：

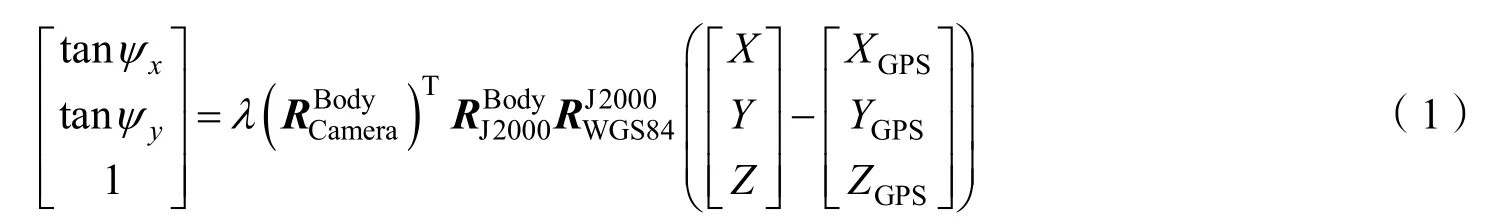
式中 (ψx,ψy)為地面點對應的成像探元在相機坐標系下x向和y向的指向角；λ為比例因子；為相機在衛星本體坐標系下的安置矩陣；為J2000坐標系至衛星本體坐標系的旋轉矩陣；為WGS84坐標系至 J2000坐標系的旋轉矩陣；(X,Y,Z)為地面點在 WGS84坐標系下的物方空間坐標；(XGPS,YGPS,ZGPS)為GPS天線相位中心在WGS84坐標系下的空間坐標。

海岸帶成像儀雙相機每一波段的每一片CCD均包含了5 450個成像探元。在實際處理過程中，很難直接獲得每一個成像探元的指向角，通常采用一般多項式模型作為探元指向角模型，具體形式為[14-17]：

式中 (a0,a1,a2,a3,b0,b1,b2,b3)為探元指向角模型系數；S為探元數。

通過海岸帶成像儀分片影像與定標場參考 DOM/DEM 的密集匹配，可以獲得大量高精度地面控制點，再根據式（1）～（2），便可精確求解出每一片CCD的定標參數[12,18]。

1.2 虛擬化拼接

海岸帶成像儀雙相機經過在軌幾何定標處理后，可以獲得每一片CCD在歸一化焦平面上的精確位置。在此基礎上，根據成像探元在焦平面上的起止位置、探元個數等參數，設置一個虛擬長線陣CCD，如圖1所示。圖1中，B1～B4表示海岸帶成像儀的4個波段；xf of yf為歸一化焦平面坐標系，其xf軸（垂直于探測器線陣方向）和yf軸（平行于探測器線陣方向）分別平行于相機坐標系的x軸和y軸。

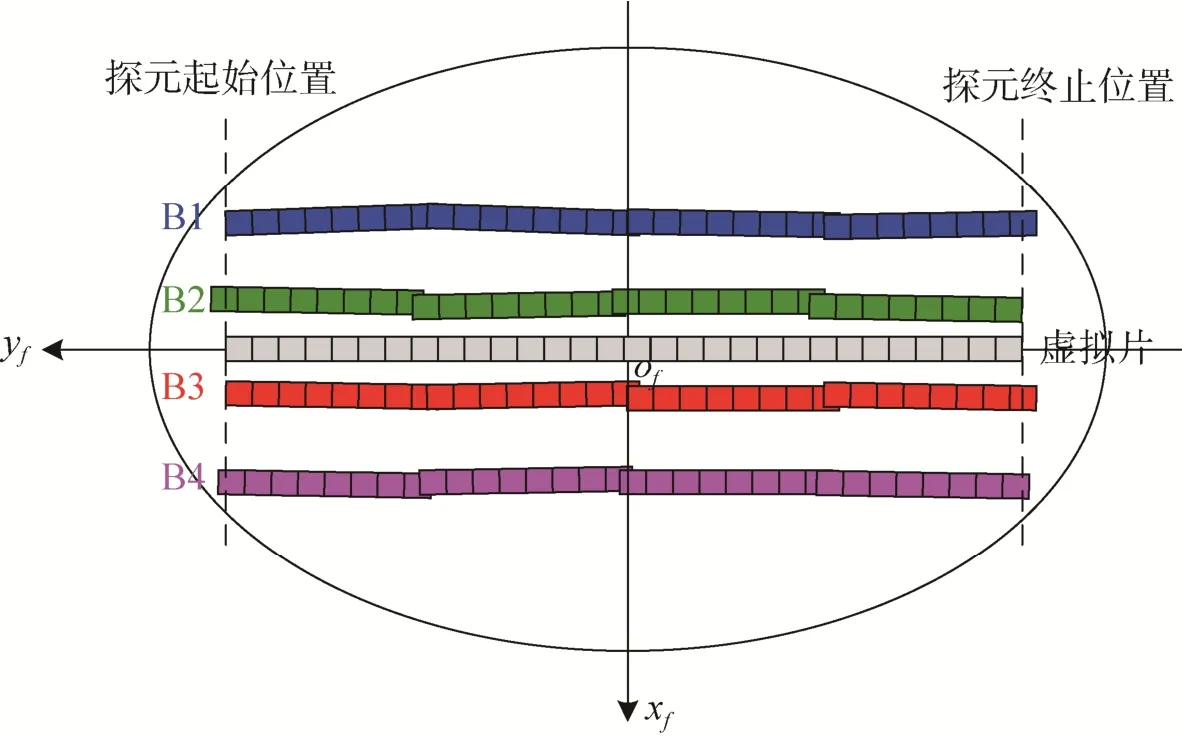
圖1 虛擬長線陣示意Fig.1 A sketch map of the virtual linear array

虛擬長線陣 CCD的探元指向角模型可表示為：

海岸帶成像儀雙相機虛擬化拼接的主要步驟包括：1）根據衛星軌道和姿態參數、影像成像時間、分片CCD內外定標參數，分別構建分片影像的成像幾何模型；2）根據衛星軌道和姿態參數、影像成像時間、虛擬片CCD內外定標參數，構建拼接影像的成像幾何模型；3）根據拼接影像的成像幾何模型，將拼接影像上的像點投影至物方高程面上，得到物方投影點；4）根據分片影像的成像幾何模型，將物方投影點投影至分片影像上，得到像方投影點；5）對像方投影點進行灰度重采樣，將得到的灰度值賦給拼接影像上對應像點；6）重復步驟3）至5），直至完成拼接影像上所有像點，得到拼接后的影像。

2 試驗及其結果分析

2.1 試驗設計

本文利用5景HY-1D衛星海岸帶成像儀分片影像開展試驗驗證，各景影像基本參數如表1所示。其中，第一景影像作為定標景，用于雙相機在軌幾何定標驗證，得到每一片 CCD的精確成像參數。在此基礎上，其余影像作為測試景，用于雙相機幾何拼接精度驗證。對于雙相機幾何拼接而言，4個波段影像具有等同性，本文僅以第二波段影像進行試驗驗證。

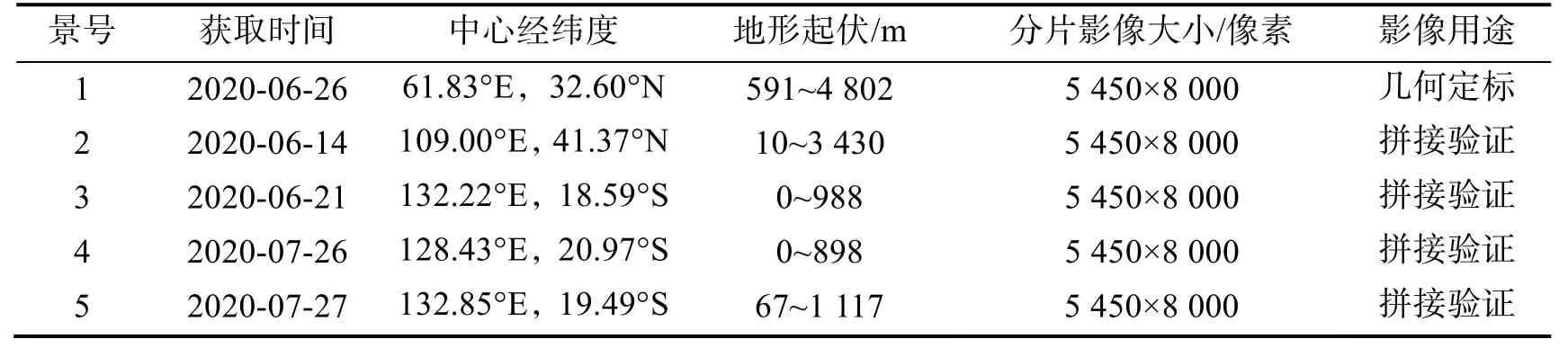
表1 各景影像的基本參數Tab.1 General parameters of each image

2.2 在軌幾何定標精度分析

鑒于 HY-1D衛星海岸帶成像儀星下點影像的空間分辨率約為 50m，本文以 15m空間分辨率的LandSat-8 ETM DOM和90m空間分辨率的SRTM DEM作為定標參考數據，進行海岸帶成像儀雙相機在軌幾何定標。其中，LandSat-8 ETM DOM的平面精度約為12m[20]，相當于海岸帶成像儀影像的0.24像素；90m分辨率SRTM DEM的高程精度約為16m[21]，引起的平面最大誤差約為9m，相當于海岸帶成像儀影像的0.18像素。由此可見，由參考DOM和DEM誤差引起的理論定標誤差約為0.3像素。

通過海岸帶成像儀分片影像和參考數據的密集匹配，在4片影像上分別匹配獲得了75 611、55 563、62 352和98 513個高精度地面控制點，分布情況如圖2中紅色標志點所示。

圖2 地面控制點在海岸帶成像儀定標景分片影像上的分布Fig.2 Ground control point distributions in sub-images of the CZI calibration scene

利用匹配獲得的控制點，根據1.1節介紹的在軌幾何定標方法，分別求解4片影像所對應CCD的定標參數。在此基礎上，分別構建4片影像的有理函數模型，并利用該模型將每一個控制點由物方投影至像方，再統計像方投影點的像平面坐標及其對應匹配點的像平面坐標之間的最大誤差和中誤差，作為幾何定位精度列于表2。為便于比較分析，表2同時列出了利用在軌幾何定標前的初始相機參數獲得的幾何定位精度。定標前、后的控制點殘差分布分別如圖3和圖4所示。

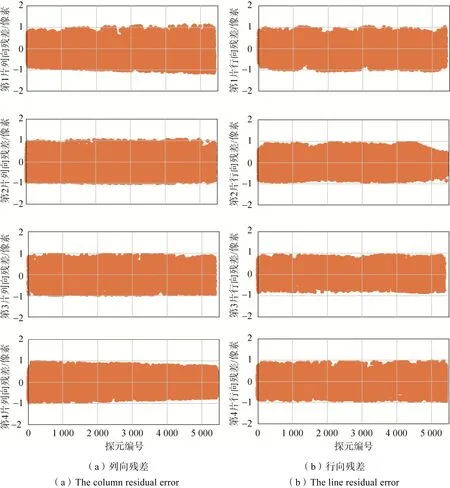
圖4 海岸帶成像儀定標景控制點殘差分布（定標后）Fig.4 Residual error distribution of ground control points in the CZI calibration scene（after calibration）

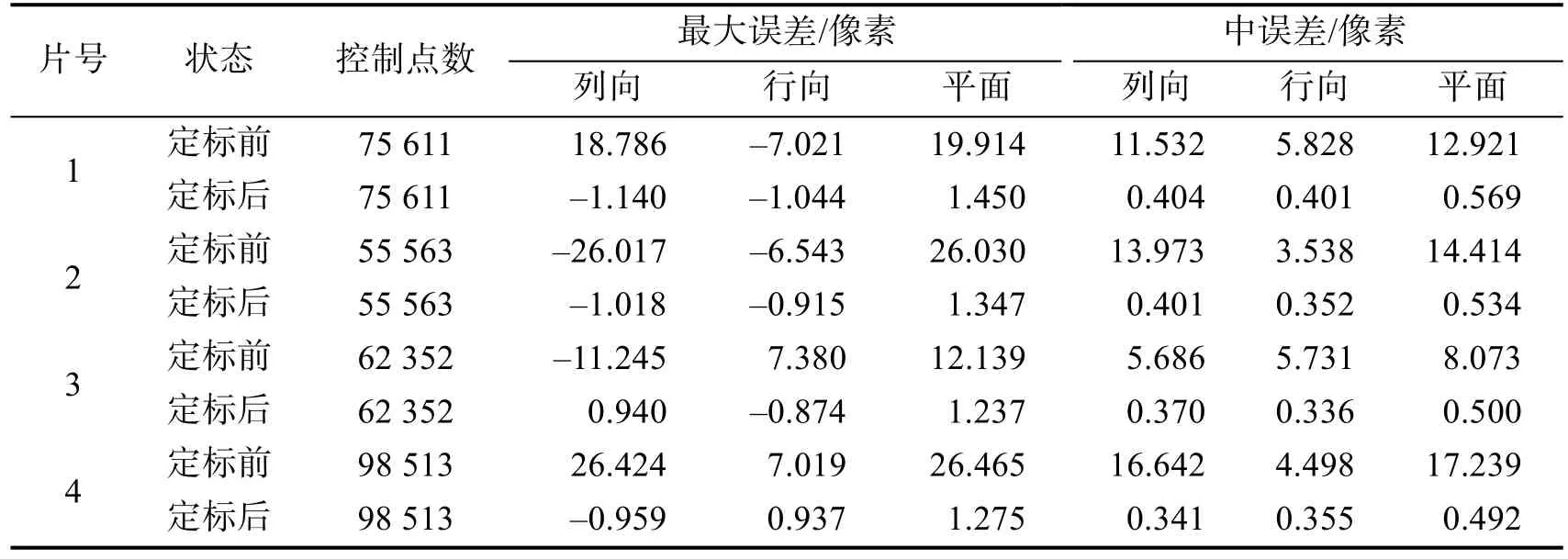
表2 海岸帶成像儀定標景幾何定位精度Tab.2 Georeferencing accuracy of the CZI calibration scene

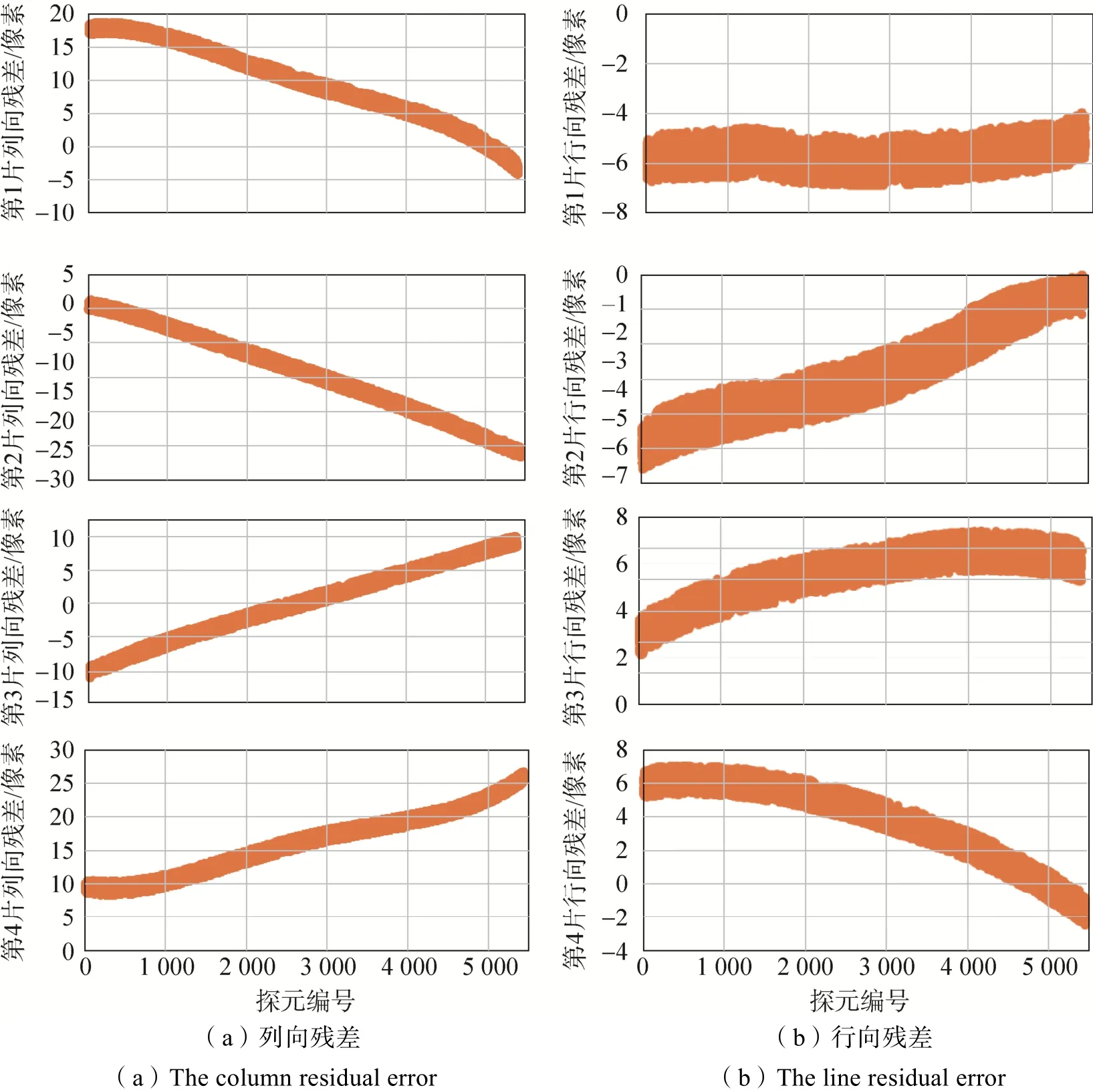
圖3 海岸帶成像儀定標景控制點殘差分布（定標前）Fig.3 Residual error distribution of ground control points in the CZI calibration scene （before calibration）

分析表2與圖3～4中的試驗結果，可以看出：

1）在軌幾何定標之前，定標景4片分片影像存在8～17個像素的定位誤差。究其原因在于，相比于衛星發射前實驗室測量的相機成像參數，衛星發射過程中由于其加速度過大、振動劇烈等因素導致相機成像參數發生了不同程度的改變。從圖3顯示的控制點殘差分布可以明顯看出，相機成像參數改變引起的定位誤差既包括線性誤差，也包括非線性畸變，且相鄰兩片影像重疊區域的定位誤差并非完全一致，必然導致相鄰兩片影像之間存在不同程度的拼接錯位（如圖5（a）所示），無法滿足海岸帶成像儀雙相機高精度幾何拼接的應用需求。

2）經過在軌幾何定標處理，可以有效消除分片影像定位結果中的線性誤差和非線性畸變（如圖4所示），得到每一片CCD的精確成像參數。因此，分片影像的定位精度得到了明顯提升，相鄰片影像之間的拼接錯位亦得到了明顯消除（如圖5（b）所示），為海岸帶成像儀雙相機高精度幾何拼接提供了良好的幾何基礎。

圖5 海岸帶成像儀定標景第二片和第三片影像拼接效果Fig.5 The stitching result of the second and the third sub-images of the CZI calibration scene

2.3 雙相機拼接精度分析

按照1.2節介紹的海岸帶成像儀雙相機虛擬化拼接方法，對表1中第二景至第五景分片影像分別進行拼接處理，得到拼接后的影像。為了充分驗證雙相機拼接精度，這里仍以15m空間分辨率的LandSat-8 ETM DOM和90m空間分辨率的SRTM DEM作為參考數據。通過拼接影像與參考數據的影像匹配處理，在4景影像的整個影像范圍內分別匹配獲得了12 478、5 263、2 773和3 463個高精度控制點，點位分布如圖6所示。從圖6中可以看出，控制點有效覆蓋了拼接影像整個列方向，滿足雙相機拼接精度分析對控制點的點位分布要求。另外，拼接影像內部幾何精度既可以體現分片影像的內部幾何一致性，也可以體現拼接影像整體的內部幾何一致性。因此，本文通過拼接影像內部幾何精度來分析雙相機拼接精度。

圖6 海岸帶成像儀測試影像控制點分布Fig.6 Ground control point distribution of the CZI test images

通常情況下，光學衛星影像的內部幾何精度應達到優于1個像素，才能夠滿足高精度應用處理需求。本文在拼接影像有理函數模型的基礎上，利用仿射變換模型消除衛星軌道和姿態參數中的測量誤差，并統計像方投影點的像平面坐標及其對應匹配點的像平面坐標之間的最大誤差和中誤差，作為拼接影像的內部幾何精度，結果如表3所示。其中，第二景測試影像的控制點殘差分布如圖7所示。

表3 海岸帶成像儀測試景內部幾何精度Tab.3 Internal geometric accuracy of the CZI test images

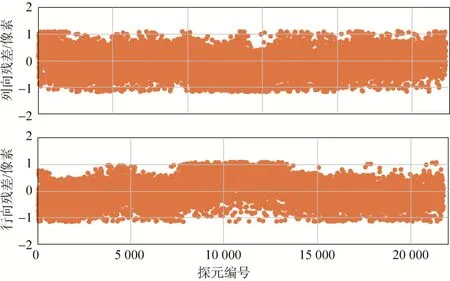
圖7 海岸帶成像儀第二景測試影像控制點殘差分布Fig.7 Residual error distribution of ground control points in the second CZI test image

從表3中的試驗結果可以看出，海岸帶成像儀雙相機拼接影像的內部幾何精度優于0.8像素，滿足優于1個像素的高精度應用需求。對比圖7和圖3可知，拼接影像定位結果不存在非線性畸變。由此可見，HY-1D衛星海岸帶成像儀具有良好的幾何性能，本文介紹的海岸帶成像儀雙相機幾何拼接方法亦是切實可行的。

3 結束語

根據HY-1D衛星海岸帶成像儀雙相機的物理結構及成像機理，本文重點介紹了一種基于虛擬化拼接的海岸帶成像儀雙相機高精度幾何拼接方法。首先，通過在軌幾何定標處理，獲得每一片CCD的精確成像參數。在此基礎上，通過虛擬化拼接處理，獲得拼接后的影像。對5景分片影像數據的幾何拼接試驗結果表明，利用本文方法可以實現海岸帶成像儀雙相機分片影像的高精度幾何拼接，獲得的拼接影像內部幾何精度優于1像素，可以滿足后續定量產品處理對海岸帶成像儀1級標準影像產品的幾何質量需求。

致 謝：感謝國家衛星海洋應用中心提供的“海洋一號”D衛星海岸帶成像儀測試數據。