基于M估計的三維容柵微小位移系統參數估計
金懷智,李新娥,王 睿,楊偉藝,顧 攀
(中北大學 電子測試技術重點實驗室,山西 太原 030051)
0 引 言
微小位移測量經過多年的研究取得了長足的發展,是精密測量技術的研究熱點之一[1],測量方法有以下幾種:激光傳感器、LVDT傳感器、PSD位置敏感器件、電容位移傳感器等[1,2]。本文所測系統為三維容柵位移系統,主要特征是容柵傳感器電極呈柵極分布,具有測量精度高、運行速度快、體積小、結構簡單、總體功耗低等優點,是狹小空間微小位移測量的理想儀器[3]。
最小二乘法(ordinary least square,OLS)是對未知參數估計的強大數學工具,具有無偏性和有效性[4]。最小二乘法在解決目標函數最優解問題時,會人為地忽略誤差方程系數矩陣中的隨機誤差,這種含有離群值的線性估計,結果會受到不良影響,甚至產生錯誤結論,因此需要一種穩健回歸解決上述問題。
對現有線性回歸模型進行研究,提出使用M估計加權最小二乘法線性回歸分析三維容柵微小位移。通過理論推導確定基本模型,并對測量位移進行正態性分析,確保模型為線性系統;采用Huber robust函數作為加權函數,具有較高的穩健性和估計效率;使用皮爾遜相關系數分析法驗證測量值和預測值的相關性。實驗測試結果表明,該算法在有離群值時具有良好的擬合效果,系統參數估計更準確、穩定,對三維容柵微小位移系統的安裝調試具有顯著指導作用。
1 測試系統設計
1.1 傳感器設計
容柵傳感器由多條平板電容并聯,主要的工作部件為靜柵和動柵[5],如圖1所示。當動柵忽略邊緣效應時,單塊柵極的初始電容和正對面積記為C0和S0,容柵傳感器的電容為
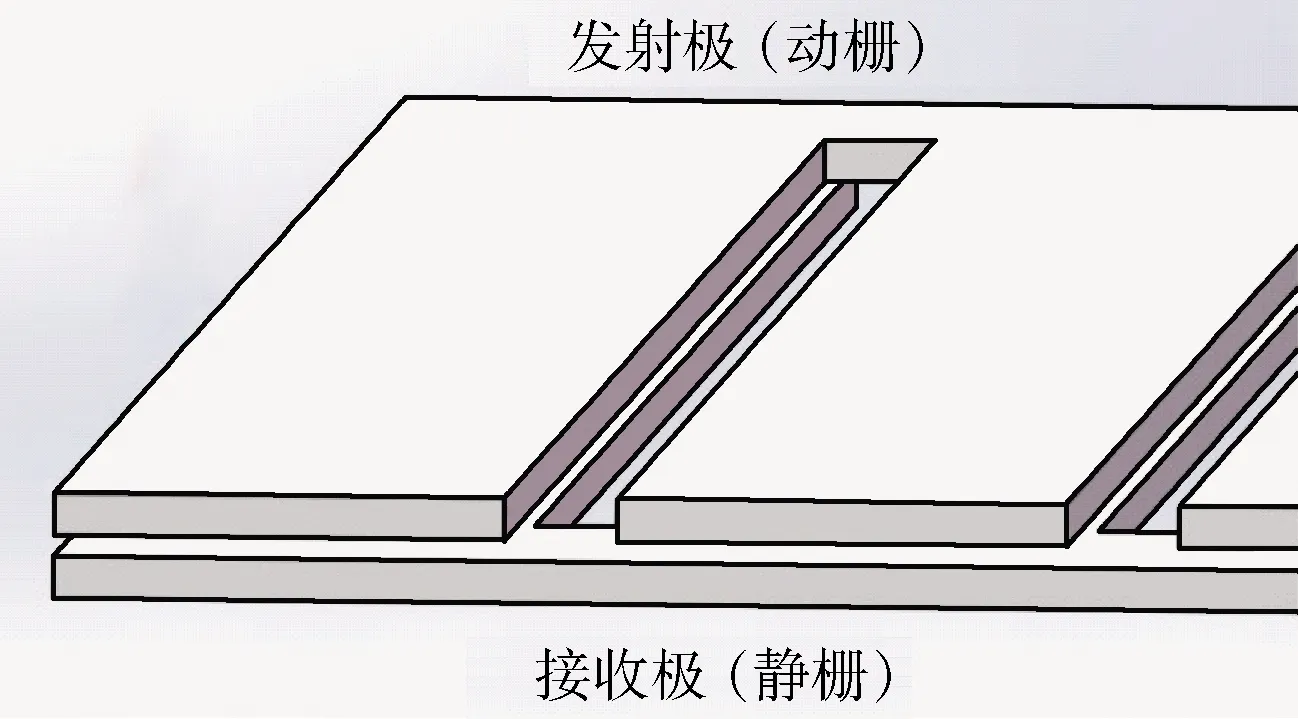
圖1 容柵結構
(1)
式中:n為傳感器柵極條數,ε0為真空介電常數,近似為8.854×10-12F/m,εr為板級間介質的相對介電常數,ε為總體介電常數,S0為單條柵極極間相對面積,S為總極間相對面積。
1.2 信號采集單元
本設計共有3個通道,分別是通道1(動柵X)、通道2(動柵Y)、通道3(動柵Z),安裝在其中一個同心球外側,代表著XYZ這3個方向的位移,其共同的靜柵被安裝于另一個同心球內側。
三維容柵微小位移測試系統信號采集單元原理框架如圖2所示。

圖2 采集單元原理框架
4個恒流源給容柵傳感器供電,使用電子開關開闔傳感器。由于容柵傳感器的電容變化量很微小(約為1 pF/0.05 mm),電磁干擾,溫度變化引起的噪聲信號會在單路放大器輸入端產生共模干擾。采用差分放大電路可以很好地解決這個問題,達到放大差模信號、抑制共模信號的目的。
任一通道電容與電壓的關系
(2)
式(2)和式(1)聯立得
(3)
式中:U為傳感器兩端模擬電壓,Q為直流源輸出電荷量。
本設計通過電子開關實現PWM波開關控制,當動柵發生位移造成相對面積的改變所引起的電容值變化,可判斷微小位移的大小及方向。
1.3 傳感器安裝與布置
三維容柵傳感器微小位移測量系統是為了測量兩個同心球的相對轉動情況,容柵傳感器具有結構輕薄的特點,可以便捷安裝在球體表面和內側。
據文獻[2]中對二維容柵微小位移系統的研究,三維傳感器采取正交式安裝方法,以XY坐標軸形成一個平面,再向上取一個與XY都正交的Z軸,形成三維坐標系。容柵傳感器布置在兩個同心球體表面,由于球面具有較大曲率,故安裝傳感器時可將其等效為4塊平面容柵傳感器,其中一個球面內側安裝一塊接收級(靜柵),另一個球面外側安裝3塊相互正交的發射極(動柵),每一組動、靜柵測量一個方向的位移變化,如圖3(a)所示。

圖3 容刪安裝及改進
實際安裝時,當動、靜柵均采用方形的容柵傳感器時,拿X通道分析,初始相對面積為Sx0,靜、動柵邊長為L,三通道位移分別為x、y、z,由于容柵傳感柵極間的d由同心球間距決定,分析時認為d為定值,其電壓模型為
(4)
式(4)在模型分析時,X通道的電壓涉及兩個方向的位移,模型參數較為復雜,不適合在操作現場做參數估計。為了避免不同通道位移相互影響,使用3塊10 mm×10 mm的靜柵,與先前無異,成品字形排布;使用3塊5 mm×10 mm的動柵,寬度縮小一半,當Z方向發生位移時,X通道由于靜柵寬度大于動柵寬度,在量程范圍內(0.3 mm~1 mm)Z方向的位移不對ΔSX產生影響,改進后的安裝布置如圖3(b)所示。
2 參數估計算法
2.1 模型分析
3個通道相互獨立,對通道X做分析,根據式(4)可知其電壓位移模型為
(5)
其中,k=Q/ε,x、y、z為3個方向的位移量,Sx0、Sy0、Sz0為動柵與靜柵的初始相對面積,L為靜柵邊長。分別對三通道使用此位移模型,并做變形以適應線性回歸系統
(6)
2.2 系統誤差分析
一般情況下,容柵傳感器的電場在柵極邊緣處不能均勻分布,產生邊緣效應,是傳感器設計過程中必須要考慮的因素。邊緣效應導致傳感器靈敏度下降和電容值非線性增加,實際電容值在理論電容值基礎上加上附加電容值,即:C實際=C理論+C邊緣。
C邊緣不是一個常量,其與柵極數量、柵極厚度、柵極間距均有關聯,且在傳感器信號動態變化時尤為嚴重[6]。在加工工藝、成本制造等各方面因素影響下,盡可能減小極板間距和極板厚度、控制柵極對數并適當增大初始電容C0,使邊緣效應造成的影響最小[7]。
2.3 M估計線性回歸算法
2.3.1 M估計背景
M估計(maximum likelihood type estimation,M-Estimation)是一種迭代加權最小二乘法,屬于穩健回歸的一種[8],由Huber于1964年提出,也被稱為廣義最大似然估計,其原理是給每個樣本點不同的權重,偏差較大的樣本點權重小,偏差較小的樣本點權重大,異常點出現時不會對擬合方程產生較大影響。
2.3.2 M估計運算準則
M估計的運算方法有很多,而迭代加權法(iteratively reweighted least squares,IRLS)由于其算法類似于最小二乘法,易于編寫和移植,故而得到廣泛的應用。
對于有i個影響因素的自變量矩陣X=[x1,x2,…,xi],其與因變量Y的關系如下
Y=β1x1+β2x2+…+βixi+b
(7)
最小二乘法的殘差函數為
(8)
運算準則為
(9)
M估計采用迭代加權最小二乘回歸系數,根據前一次回歸殘差確定各樣本權重,殘差函數被改寫為
(10)
則M估計的運算準則為
(11)

ρ為影響函數,一般滿足以下條件[9]:
(1)ρ(r)≥0;
(2)ρ(0)=0;
(3)ρ(-r)=ρ(r);
(4)If|ri|≥|rj|,thenρ(ri)≥ρ(rj)。
為了保證M估計的回歸系數通因變量的觀測單位無關,希望M估計結果具有尺度同變形,即滿足
(12)
為滿足上式條件,估計回歸系數β需將殘差ri標準化,除以某個尺度參數σ,得到標準化殘差ri/σ。
M估計的運算準則即定義為如下

(13)
實際運算中,Hampel于1974年提出以ri(β)觀察點的絕對離差中位數(median absolute deviation,MAD),除以常數0.6745作為穩健估計尺度σ[10]。
MAD是一種衡量數據離散分布的魯棒性測量方法,同時也可表示樣本的總體參數。對于單變量數據集M=[M1,M2,…Mn],其MAD公式為
MAD=median(|Mi-median(M)|)
(14)
2.3.3 常用的影響函數
在穩健估計中,有幾種常用的影響函數,以及對應的導函數和權因子:
(1)最小二乘法
最小二乘法是一種特殊的M估計
Ψ(u)=u
(2)絕對和極小法(LAD估計)
ρ(u)=|u|
Ψ(u)=sign(u)
LAD估計又稱L1估計,是Lp估計的一種,p值越小,β收斂到最小值需要的迭代次數越多,是一種較為準確但收斂較慢的影響函數。
(3)Huber法
本文選用Huber loss[11,12],降低了對離群點的懲罰程度,適合數據接近正態分布的情況,是一種具有良好魯棒性的影響函數。
Huber提出一種加權函數[11-13]
|u|≤c

|u|≥c
Ψ(u)=u
|u|≤c
=c·sign(u)
|u|≥c
其中,c是常數,通常默認為1.345,為Huber的尺度參數。Huber算法可以看作將最小二乘法和LAD法相結合。當殘差絕對值較小處,使用最小二乘法;殘差絕對值大處使用LAD。這種估值方法既能提高系統的準確性,也有較高的估值效率。
Huber函數在不同尺度下的function如圖4所示。

圖4 Huber function 原函數和導函數圖像
2.3.4 M估計具體算法
對殘差函數的表達形式預處理:
(1)式(10)中目標函數ρ(ri)對β求偏導得
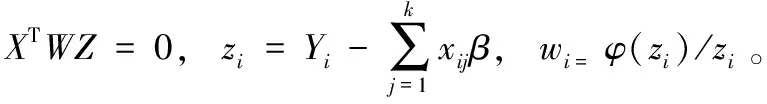
(2)對線性方程組向量化得XTWe=0
(3)將Y=Xβ+e代入得XTWXβ=XTWY
(4)得β=(XTWX)-1XTWY
具體算法步驟為:
(1)建立U=xβ+b的線性方程組,根據OLS求出初始殘差e0;
(2)標準化殘差得到zi,由wi=φ(zi)/zi作為樣本的初始權重;
(3)又由β=(XTWX)-1XTWY求出新的β(i)以求得新的殘差代替β(i-1);
(4)返回(2)進行迭代依次計算β(i),給定殘差迭代閾值ξ,當|β(k+1)-β(k)|<ξ,此時滿足收斂條件,βM=β(k+1)。
2.3.5 M估計對測試系統的作用
在本系統設計中,M估計主要作用是在系統標定完成后,實際測試時預測系統參數。微小位移系統安裝時,由于同心球內空間狹小,一旦安裝完成很難調整容柵傳感器柵極相對位置,M估計可以及時比較測量值和預測值的殘差,對系統的安裝調試具有顯著意義。
2.3.6 皮爾遜相關性分析
為了分析OLS和M估計的擬合優度,采用卡爾皮爾遜提出的皮爾遜相關系數法(Person correlation coefficient),又稱皮爾遜積矩相關系數,是一種準確度量兩個變量之間關系密切程度的統計學方法[14]。
一般情況下,皮爾遜相關具有如下約束條件:
(1)兩個變量間有線性關系;
(2)變量為連續變量;
(3)變量均近似符合正態分布,且二元分布也符合正態分布;
(4)兩個變量均為獨立變量。
對于兩組變量X,Y,通過實驗得到若干組數據對,記為(xi,yi)(i=1,2,…,n),樣本的總體相關系數數學表達式為
(15)
估算樣本的協方差和標準差,則皮爾遜相關系數表達式為
(16)
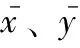

表1 皮爾遜相關系數的關聯程度
樣本相關系數是通過樣本數據計算得到,其值受到樣本的隨機性、數量等影響。因此需要對樣本相關系數做顯著性檢驗,即求P-value。Z檢驗一般用于大樣本均值差異性檢驗的方法,不太適合本測試。T分布檢驗是一種小樣本分布檢驗,較為適合本測試,構造一個統計量t,構造方式如下
(17)
這個統計量是符合自由度為t-2的T分布。其中n為樣本的數量,r是皮爾遜相關系數ρX,Y。
定義原假設H0為r等于0,即不存在線性相關性,通過T分布表得出滿足拒絕H0的顯著性水平α,顯著性檢驗是“小概率事件實際不可能原理”,α越接近于0,越說明原假設不成立,數據具有統計學意義。
3 實驗測試和數據分析
3.1 正態性分析
線性回歸參數估計要求被測數據集滿足或近似滿足正態分布。考慮到測試數據正可能不具有良好正態性,有以下幾種處理手段:
(1)若方差正比于均值,進行平方根轉換;
(2)若標準差正比于均值,進行對數轉換;
(3)還可以采用Yeo-Johnson或Box-Cox變換,這是針對隨機變量正態性較差時做的數據預處理。當預處理后的數據偏離原始數據的性質時,可認為該數據不適用正態性校驗方法,轉而采用非參數檢驗方法如秩和檢驗、中位數評分檢驗等。
位移數據由系統模型搭建完成后采樣得到,利用SPSS Statistics數據分析軟件對3個通道所得數據使用直方圖和P-P圖兩種統計學方法進行正態性分析[15],驗證結果如圖5所示,可知XYZ三通道采樣數據具有較良好的正態性。

圖5 三通道正態性校驗
3.2 數據標定與分析
圖6為此系統的標定裝置,其作用是:①檢測容柵傳感器性能參數是否符合預定標準以及理論模型是否正確;②提供一個標定值(認定是真值)。

圖6 標定測試裝置
測試時,通過調節標定平臺上的千分尺旋鈕精確控制動柵和靜柵之間的距離,此裝置最小分辨率為0.01 mm,雖精度沒有達到0.001 mm,但可估讀到0.001 mm,滿足電路調試和數據標定0.05 mm步長的要求。
選定0.3 mm~0.95 mm為標定距離范圍,0.05 mm為步長,由于電壓倒數只是統計學上方便計算的操作,無實際的物理意義,也沒有對應的物理單位,所以還是使用電壓單位V,得到如表2所示的關系表。
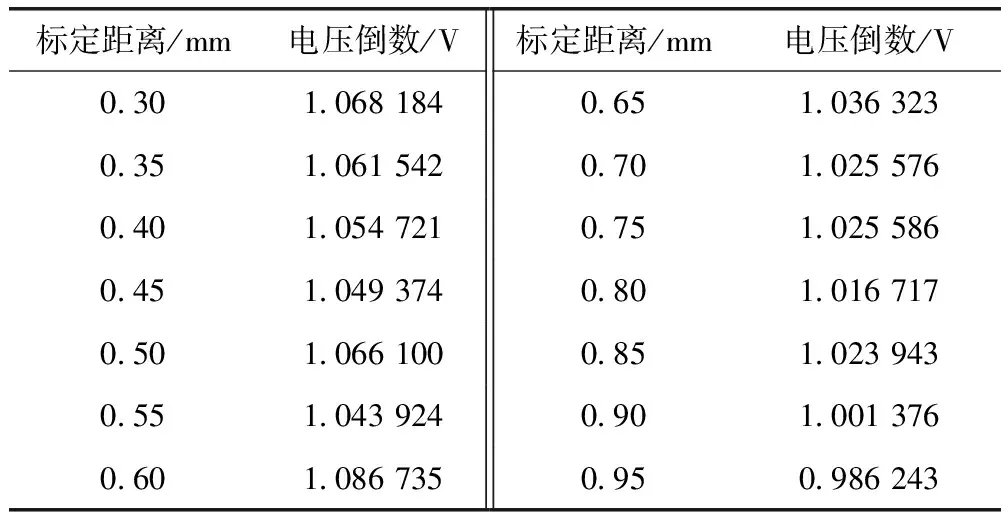
表2 標定距離和采集電壓倒數
對標定距離x和采集電壓的倒數1/UX使用Matlab軟件做OLS和M估計線性回歸參數估計,標定了14組數據,其擬合效果如圖7所示。
據圖7可知,擬合直線對于偏差過大的離散點敏感性降低,避免了標定過程中因操作失誤等因素造成系統擬合直線偏移。

圖7 X通道電壓倒數與位移關系
使用此算法分別得到3個通道M估計預測線性回歸方程為
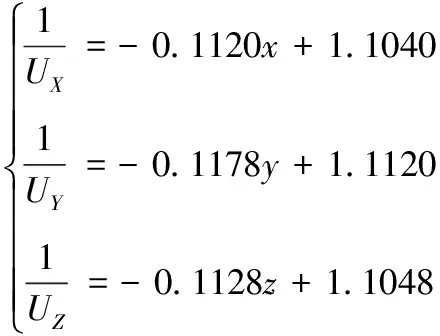
(18)
模型搭建完成后,在標定平臺上對系統標定,驗證測試距離與標定距離的相對誤差,同時對比OLS預測距離和M估計預測距離相較于測試距離的相對殘差,分析兩種算法的優劣。
表3、表4、表5為標定平臺三通道測量數據,Z通道在測量0.40 mm這一組數據時,出現了明顯的離群值,經檢查,認為是標定時出現誤觸導致裝置的偏移,容柵傳感器相對面積發生變化造成測量的不準確,經重新多次測量得數據為0.398 mm。三通道相對誤差符合預期值,相對誤差均小于3%。分別計算兩種算法相較測試距離的相對殘差:(測量值-預測值)/測量值×100%,在(0.30 mm,0.40 mm),雖然OLS預測距離比M估計距離和實測距離都要更接近標定距離,但算法預測主要作用是校準傳感器,而不是預測真值,評價其擬合優度指標是相對殘差,且在(0.40 mm,0.60 mm),OLS預測距離逐漸偏離真值,綜合三通道算法預測表現,M估計總體優于OLS,具有良好的擬合效果和魯棒性。
將表3、表4、表5中OLS與M估計預測結果分別進行皮爾遜相關性分析,匯總結果見表6。

表3 X通道測試距離、預測距離相對殘差

表4 Y通道測試距離、預測距離相對殘差

表5 Z通道測試距離、預測距離相對殘差

表6 相關性和顯著性分析
由表6可知,經皮爾遜相關性分析,兩種算法預測值均與測量值顯著線性正相關且M估計相關性和顯著性均優于OLS。
4 結束語
本文針對三維容柵微小位移測試系統,根據先驗經驗,使用直方圖和P-P圖法對測量數據做正態性檢驗,確保模型為線性系統;提出了使用M估計的方法,克服了普通最小二乘法對離群點的敏感性,避免了因操作不當對系統擬合產生不利影響。皮爾遜相關性分析驗證了M估計預測值與測量值具有相關性和顯著性。經實驗測試,該算法提高了預測模型的可靠性,可應用于同心球內狹小空間的三維容柵微小位移系統安裝校準。
不足之處為該模型將傳感器視為平板電容,所以只能建立在較大曲率半徑的同心球上以求計算時可以忽略傳感器的曲率。對較小球體的微小位移測量仍需改進模型,使其適應更多的球體系統。

