基于真空聯合水平電滲法的水力沖挖淤泥脫水量計算方法

楊 洋，陳人瑗，邱珍鋒，王俊杰，武立清

(1.中國電建集團華東勘測設計研究院有限公司，浙江 杭州 311122；2.華東勘測設計院(福建)有限公司，福建 福州 350003;3.重慶交通大學水工建筑物健康診斷技術重慶市高校工程研究中心，重慶 400074)

城市河道疏浚一般采用低濃度淤泥疏浚方式，如水力沖挖。水力沖挖產生的疏浚淤泥含水率高、體積大、固結難，直接堆場棄置會消耗大量的城市土地資源[1-2]，增加社會矛盾和工程造價。疏浚淤泥黏粒小、沉淀慢、滲透性差、泥水自然分離時間長，傳統脫水方法無法滿足淤泥的脫水要求，開展淤泥中泥水快速分離方法的研究迫在眉睫。

許多學者對淤泥的脫水加固技術進行了研究。付冠杰等[3]提出了一種堆載吹填淤泥并同步真空預壓加固技術，將吹填淤泥加固及軟土地基加固兩階段施工整合到一個真空預壓周期內完成以縮短造陸工期，但設置堆載所需要的材料成本和時間成本較高。房營光等[4]采用以砂墊層和豎向砂井為排水系統的真空預壓法，進行了電滲法與真空預壓法聯合作用加固堿渣土以及軟黏土的室內試驗研究，證明了真空預壓聯合電滲法的有效性。王軍等[5]通過室內試驗發現，合理地設計電滲聯合真空預壓法，可以使兩種作用產生相互促進的效果，電滲法可以提升遠離排水板土體的加固效果，真空預壓法可以降低電滲陰極的含水率。Wang等[6]采用電滲聯合真空預壓法處理淤泥，當真空預壓處理效果下降時再開啟電滲裝置。陶燕麗[7]發現在電滲過程中，黏土的排水速率與電流存在線性關系，以此為基礎，可以通過經驗公式計算黏土的排水量。劉鳳松等[8]開展了大面積真空-電滲降水-低能量強夯聯合地基加固方法研究。俞家銳等[9]對溫州蒼南縣江南圍墾區進行真空預壓-電滲加固現場試驗，結果表明真空預壓-電滲聯合加固法取得了良好的效果，不僅地基承載力超過了預期，且相對于真空預壓法在縮短工期上優勢明顯。儲旭等[10]結合福建省廈門市丙洲淺灘陸域形成工程實踐，將抽真空、電滲、強夯三者的優勢相結合，不但能改變傳統地基處理方式的應用局限性，而且能有效降低工程造價，縮短工期，提高處理后土體的強度，并具有無二次污染的特點。從以上研究可看出電滲固結脫水技術能有效提高軟土的固結度、縮短固結時間，解決低滲透性地基排水固結問題[11-13]。但是針對“超高含水率”的城市河道水力沖挖淤泥，真空聯合電滲法及其脫水處理效果評價方法的研究還較少[14]。已有的真空聯合電滲技術[15-18]存在以下問題：①淤泥處理堆場中淤泥往往深度較淺，真空預壓法的經濟性不能體現；②電滲法的電極往往是豎直布置，處理后的電極之間產生自上而下的貫穿裂縫，這種縱向裂縫直接阻斷了陰陽極之間的電流，嚴重影響電滲效果。

佘鵬等[19]通過試驗對比了水平電滲和豎向電滲的固結效率，結果表明水平向電場的脫水效果明顯優于豎直向電場的脫水效果，水平向電場降低了淤泥固結后開裂對電滲效率產生的影響，且電極區排氣問題也更易于處理。周詳等[20-21]將電極設計為水平布置，形成真空聯合水平電滲脫水法，在此基礎上，本文開展水平電滲聯合真空預壓的沖挖淤泥脫水試驗研究，提出水力沖挖淤泥脫水量計算方法。計算思路為將電滲作用與真空作用分開考慮，分別計算兩種作用排出的脫水量，最后進行疊加。將疊加之后排水量理論計算值與實測值進行對比，對計算公式進行修正，綜合考慮得出總脫水量。

1 真空作用下脫水量計算

1.1 試驗方法

為測定真空作用下淤泥的脫水量，進行了真空作用下脫水量測定試驗。在模型試驗過程中，僅使用真空排水結構對駱家溝水力沖挖淤泥進行處理，試驗布置如圖1所示。試驗槽長1.0 m，寬0.6 m，試驗槽底部布置真空濾管排水結構。將裁好的不銹鋼鋼筋按一定間距固定在薄木板上制成陽極；在直徑為5 cm的PVC管上鉆制排水孔，管外包裹兩層土工布以過濾淤泥，通過彎頭拼接陰極。陰極布置于淤泥底部，陽極布置于淤泥表面。淤泥自重作用可以有效抑制陰陽極之間的裂縫開展；陽極位置隨淤泥沉降而降低，陰、陽極距離不斷減小，電勢梯度不斷增大，有利于提升電滲脫水效果。淤泥表面至試驗槽底部高0.4 m，淤泥密度1.022 g/cm3，初始含水率為470.0%。采用底部6支真空濾管持續工作，不開啟電滲電源的試驗方案。試驗過程中監測水氣分離罐中的累計脫水量。上部淤泥最靠近陽極，此處電場強度最大，再加上重力場作用，加速上部水分向下部運移。因此呈現上部含水率變化較劇烈，底部含水率變化較緩和，中部含水率變化范圍相對較小。為減小試驗結果的誤差，每24 h取試驗槽中部淤泥測量含水率。

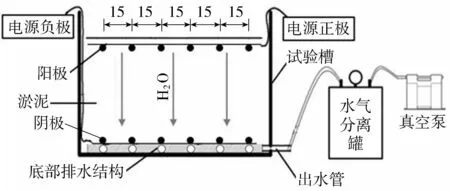
圖1 試驗布置示意圖(單位：cm)

1.2 試驗結果分析

真空作用下淤泥含水率隨時間的變化如圖2所示。從圖2可以看出，隨處理時間的增加，淤泥含水率不斷降低且降低速率逐漸減緩。前24 h含水率下降速率較大的原因可能是淤泥初始含水率大，導致大量液態水通過濾管排出；24 h后含水率近似線性減小，且含水率降低速率明顯低于前24 h，其原因是真空濾管附近淤泥的含水率下降較快，遠離濾管的水分又未及時運移到濾管附近，因此排水速度減慢。

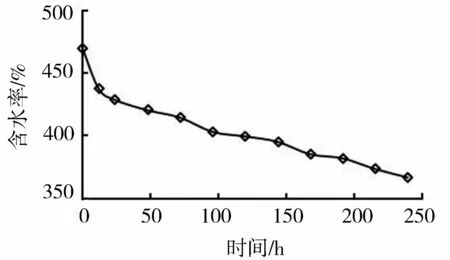
圖2 含水率隨時間變化

在試驗過程中，觀察到24 h后，水氣分離罐中的水量增加十分緩慢，僅有少量的水滴排入罐內。試驗結束后，水氣分離罐中收集到的液態水質量僅為17.125 kg。含水率測試數據表明，240 h時淤泥試樣的含水率為366.7%，較初始含水率降低103.3%。假設淤泥含水率均勻分布，已知含水率變化，淤泥脫水質量可由下式計算：

(1)

式中：mv為真空作用下脫水質量，kg；w0為淤泥初始含水率，%；w為處理后淤泥含水率，%；m0為淤泥初始質量，kg。

通過式(1)計算得到真空作用下淤泥脫水質量為44.471 kg，明顯大于水氣分離罐中收集到的液態水質量17.125 kg，可算出氣態水的質量為27.346 kg，液態水和氣態水的質量比約為3∶5。這說明淤泥中排出的水僅有一部分以液態形式貯存于水氣分離罐中，另一部分以水蒸氣的形式排出。

為了進一步探究淤泥脫水規律，分析脫水過程中脫水速率的變化情況，對比理論脫水速率與水氣分離罐實際收集到的液態水脫水速率。理論脫水速率可以表示為當前時段單位時間脫水量，即：

(2)

式中：q為當前時段總脫水速率，kg/h；Δt為時長，取為Δt=24 h。

將式(1)代入式(2)得：

(3)

脫水速率與時間的關系如圖3所示。由圖3可知，處理過程的前48 h，理論脫水速率迅速減小，與實際收集到的液態水脫水速率變化趨勢基本一致。這是由于處理前期，濾管排水結構附近淤泥含水率極高，絕大部分水以液態形式在真空與重力作用下排出，被收集在水氣分離罐中。在48～240 h時段內，理論脫水速率平均值在0.123 kg/h附近波動，而將水氣收集罐中的液態水質量視為實際脫水量換算得平均脫水速率僅為0.008 kg/h。這是由于此階段水主要以氣態排出，并未被水氣分離罐所收集到。將真空作用下淤泥的脫水過程分為兩個階段：①快速排水階段。淤泥在處理開始的一小段時間內脫水速率大，且以液態水為主，但速率衰減也很快。此階段淤泥含水率極高，液態水在重力和真空共同作用下快速排出，且重力作用對脫水速率影響很大。②穩定促排階段。在第一階段后的大部分時間內，水分主要以氣態的形式排出外界，且脫水速率在本階段平均值附近波動。此階段重力脫水作用可以忽略，真空作用為主要促進作用。

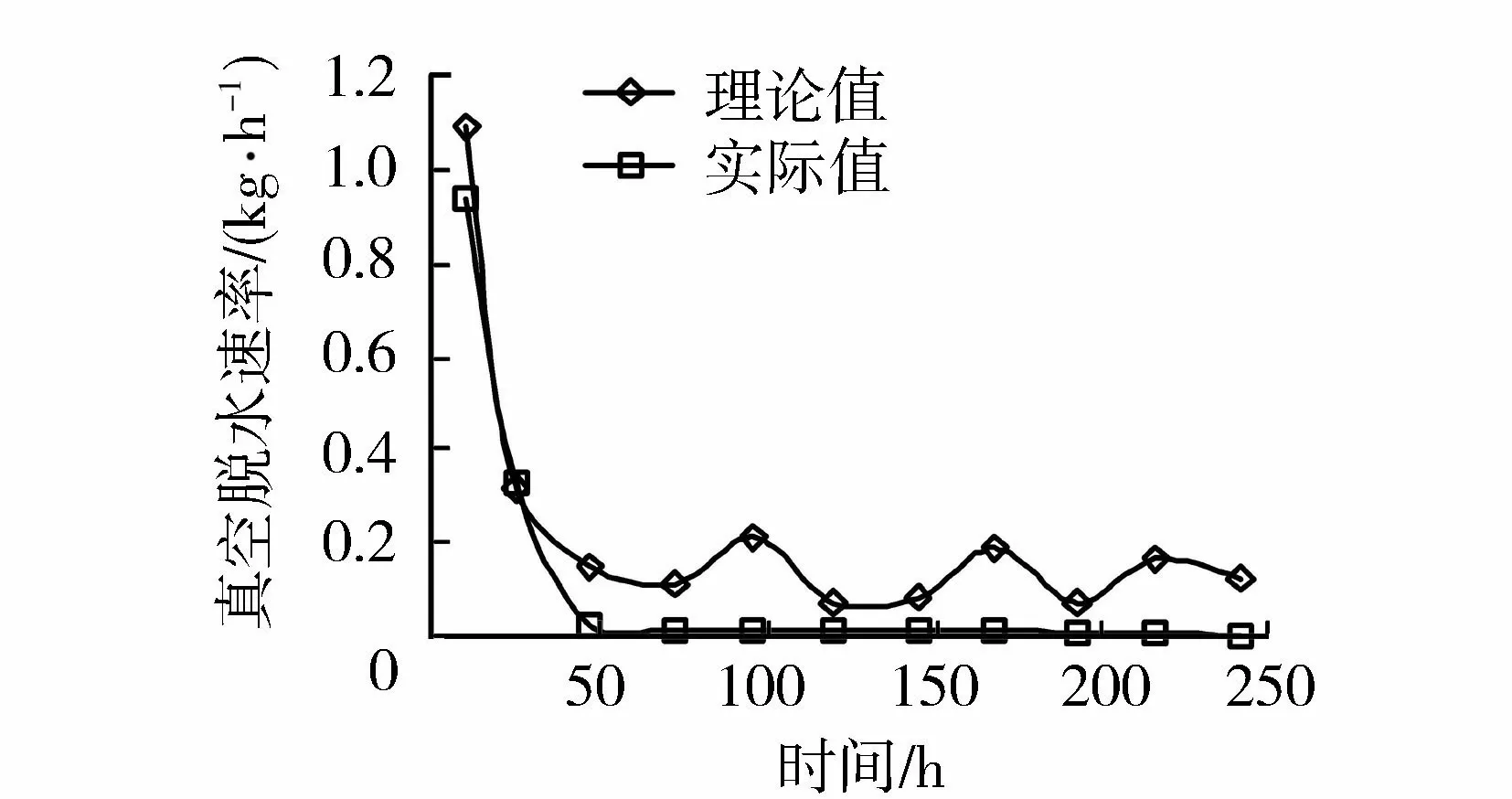
圖3 真空脫水速率隨時間變化

1.3 真空作用下脫水量計算公式

根據以上試驗結果與分析，作出以下假設：①真空作用下水均以氣態排出(快速排水階段重力作用排出的液態水歸入到電滲作用中考慮，具體計算方法在第2節中介紹)；②淤泥體內部含水率均勻減小。由此可以得出真空作用下脫水量計算公式為

(4)

2 水平電滲作用下脫水量計算方法

2.1 基本假設

已有許多學者發現，對于不同類型的土體，電滲脫水速率與電流均呈線性關系，且土體含水率與土體電導率往往存在線性關系、指數關系或二次函數關系等，可以通過一些經驗公式來計算土體的電導率[22]。假設水平電滲脫水量符合以下規律：①脫水速率與電流存在線性關系，即：q=CI，I為電流，C為與淤泥自身性質相關的常數；②電導率與含水率呈線性關系[23](式(5))、指數關系[5](式(6))或二次函數關系[24](式(7))等較為簡單的關系；③電滲過程中，土體各處含水率均勻減小，即均勻分布；④電滲作用下水分全部以液態排出并貯存于水氣分離罐中，真空促排作用排出的水分全部以氣態逸出外界。

σ=Aw+B

(5)

(6)

σ=(Aw+B)2

(7)

式中：σ為淤泥電導率，S/m；A、B、D為與淤泥的物理性質相關的常數。

2.2 公式推導

根據電滲過程中假設③和④得到土體含水率隨脫水量的變化為

(8)

式中：me為電滲脫水量，kg。

假設待處理淤泥長、寬、高分別為l、a、b，電導率可由下式計算得到：

(9)

式中：U為電源電勢，V。

根據假設①和式(9)得：

(10)

以電導率為等量關系，分別將式(10)與式(5)(6)(7)聯立，將初值條件me(0)=0代入微分方程的通解，得到電導率與含水率的不同關系式，進而得到如下3種不同的電滲脫水量me與時間t的關系式：

(11)

(12)

(13)

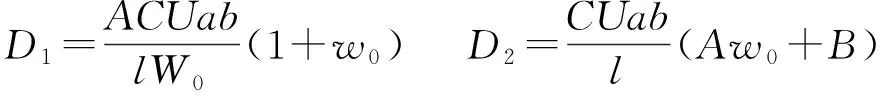
2.3 計算方法驗證

為驗證上述3種脫水量計算方法的準確性，進行了水平電滲作用下脫水量測定試驗。采用圖1試驗模型對駱家溝水力沖挖淤泥進行水平電滲脫水處理。為確定駱家溝水力沖挖淤泥電導率相關參數，模型試驗采用持續電滲的通電方式，電源電壓為30 V，淤泥初始含水率為441%。

電滲脫水速率與電流的關系如圖4所示，可見脫水速率和電流的關系符合假設①，可以用線性函數來擬合，比例常數C=0.188 6。

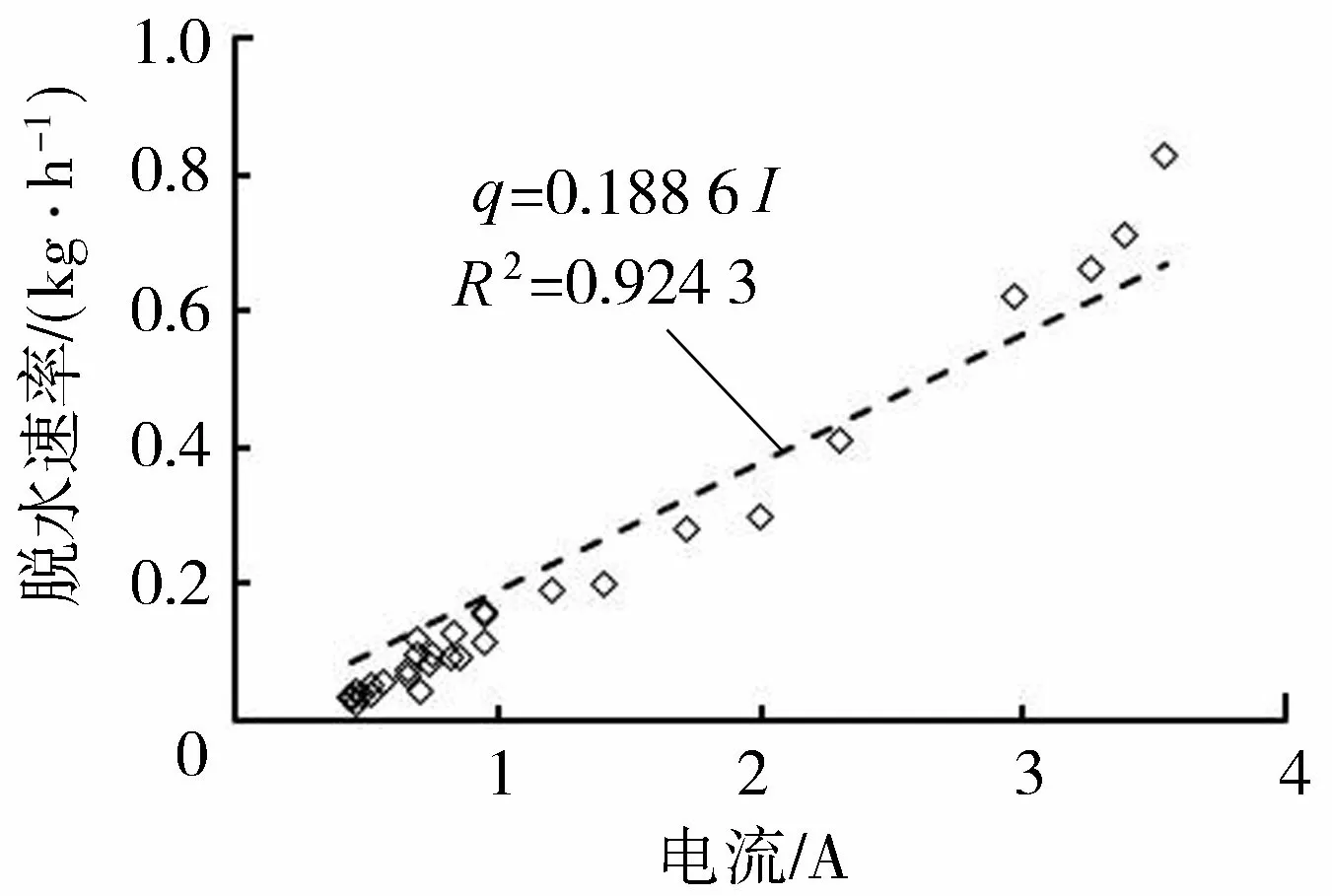
圖4 電滲脫水速率與電流關系

根據式(8)和式(9)，計算處理過程中含水率和電導率值，以含水率為橫坐標，電導率為縱坐標繪制散點圖(圖5)。采用式(5)擬合數據點時，得到駱家溝水力沖挖淤泥的材料參數A=0.471 9，B=-1.227 5；采用式(6)擬合時，得到A=0.062 7，D=1.353 4，B=-0.411 1；采用式(7)擬合時，得到A=0.520 2，B=-1.172 0。根據式(11)(12)(13)，計算得到了3種擬合方式下淤泥的電滲脫水量，見圖6。

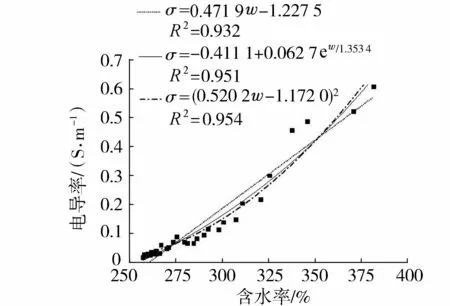
圖5 電導率與含水率關系

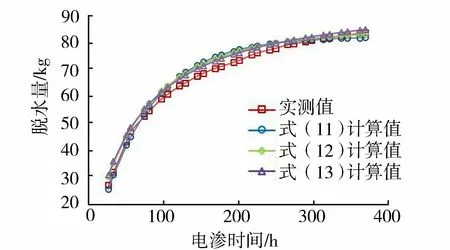
圖6 水平電滲脫水量計算結果

殘差平方和可以用來評價模型計算值與實測值的擬合程度。式(11)(12)(13)的殘差平方和分別為190.96 kg2、185.22 kg2和171.25 kg2，其中式(13)的殘差平方和最小，擬合效果最優。但總體來講，采用3種擬合方式計算出的電滲脫水量與模型試驗實測值趨勢和形態吻合均較好。這說明基于電導率的水平電滲脫水量計算方法能夠較好地擬合水力沖挖淤泥電滲脫水過程。

3 總脫水量計算方法

假設基于真空聯合水平電滲法的脫水量計算方法符合以下規律：①淤泥的總脫水量是電滲作用與真空促排作用分別作用的疊加；②脫水速率與電流存在線性關系；③淤泥的電導率與含水率具有指數關系；④處理過程中，土體各處含水率均勻減小，即均勻分布；⑤電滲作用下水分全部以液態排出并貯存于水氣分離罐中，真空作用排出的水分全部以氣態逸出外界。總脫水量計算公式為

(14)

式中：m為基于真空聯合水平電滲法的總脫水量，kg。

為了驗證本文計算方法的適用性和上文所測參數的可靠性，設置了小尺寸模型試驗，應用上文所得參數，預測模型試驗的脫水量。試驗在18 V電源電壓下進行，試樣仍采用駱家溝水力沖挖淤泥，試驗按照圖1布置，水力沖挖淤泥初始含水率為448%，淤泥密度為1.022 g/cm3。

根據第2.3節中獲得的水平電滲參數，分別計算3種擬合方式下水平電滲脫水量與實測脫水量(13.18 kg)的相對誤差和殘差平方和如表1所示。繪制水平電滲脫水量隨時間變化的關系曲線(圖7)，并與實際收集到的液態水質量進行對比。

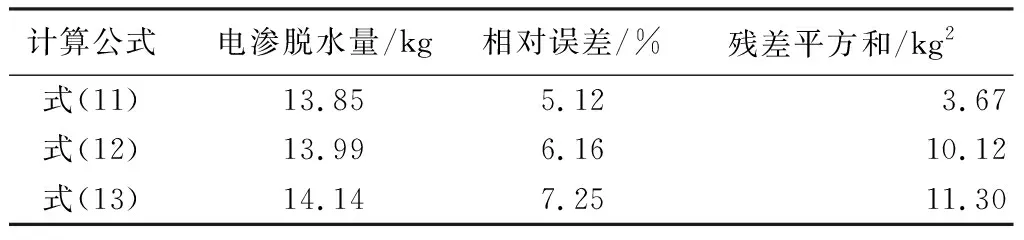
表1 水平電滲脫水量誤差統計

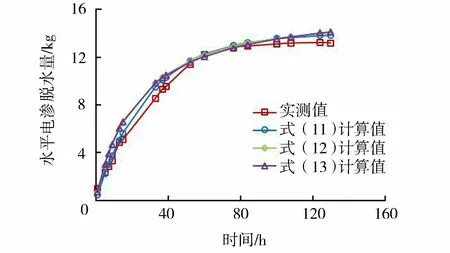
圖7 水平電滲脫水量計算結果與實測值對比

由圖7可見，采用3種擬合方式計算出的水平電滲脫水量與模型試驗實測值趨勢和形態吻合較好。這說明基于電導率的水平電滲脫水量計算方法能夠較好地擬合水力沖挖淤泥電滲脫水過程。結合表1數據可得，3種擬合方法中，式(11)的殘差平方和最小，電滲脫水量相對誤差最小，擬合效果最優。同時考慮到式(11)計算公式簡單，電滲脫水量計算僅需要確定A、B兩個參數，因此，采用線性關系擬合電導率與含水率關系對于計算駱家溝水力沖挖淤泥電滲脫水量具有一定的優越性。

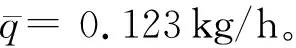
根據式(8)計算試驗結束時淤泥的理論含水率為93.30%。為了檢驗計算結果的可靠性，再一次對試驗結束時淤泥的含水率進行測試，含水率取樣點位置如圖8所示，測試結果如表2所示。

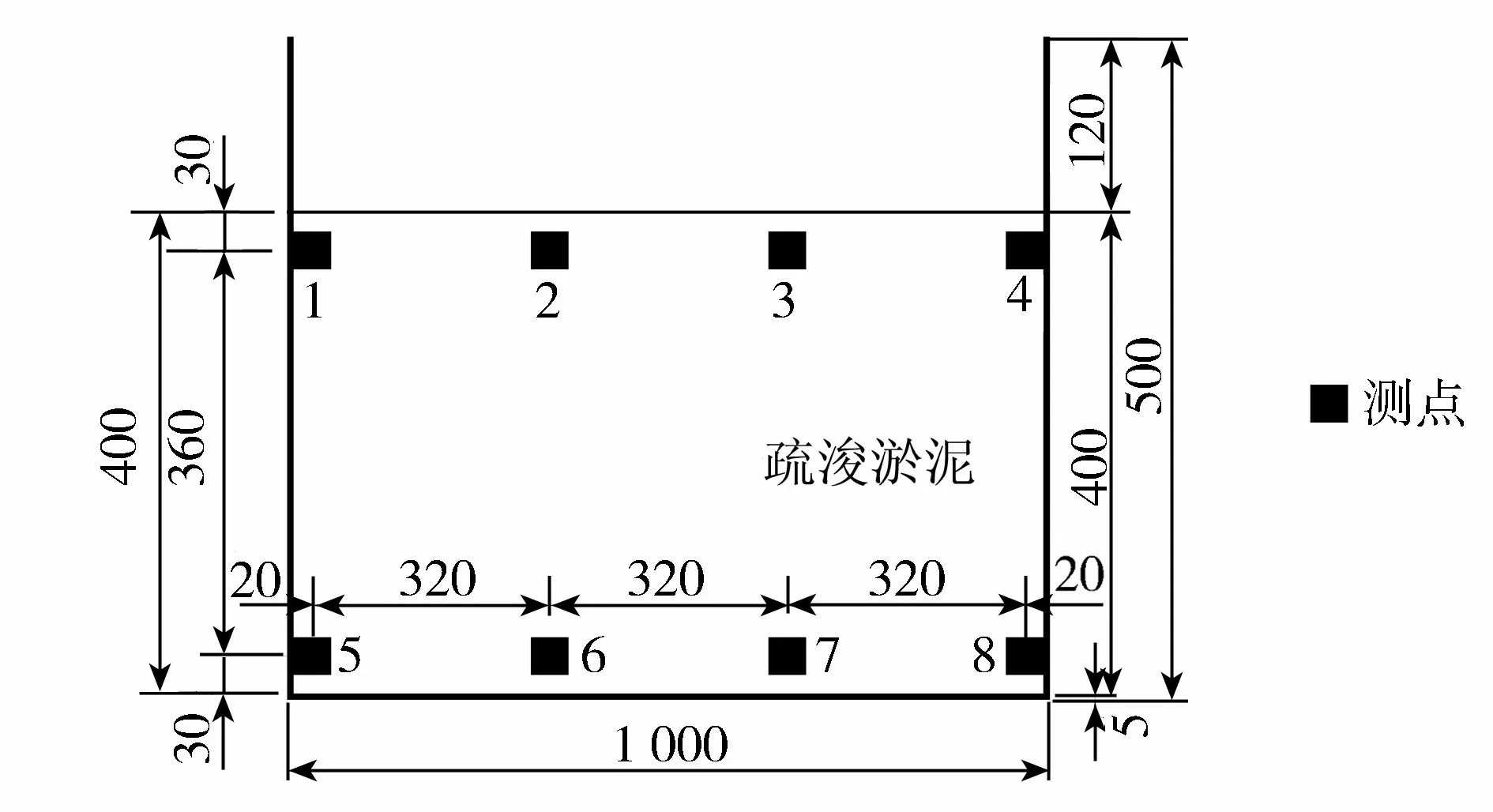
圖8 含水率測量點位置(單位:mm)

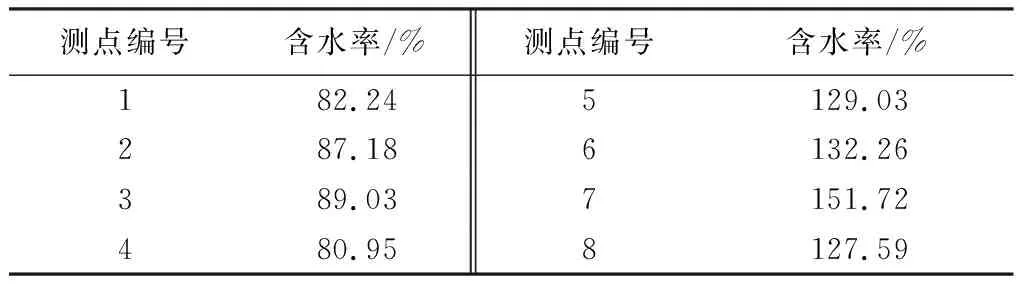
表2 含水率測試結果

由表2可得，淤泥上部較干燥，含水率平均值為86.15%，下部較濕潤，含水率平均值為137.67%，整體含水率平均值為94.23%。由于脫水處理時淤泥內部的水分流動方向是由上部的陽極流向下部的陰極，因此脫水處理后的淤泥呈現上干下濕的現象。理論含水率是假設淤泥體含水率分布均勻時通過式(8)計算出的，對比含水率測試結果，其值93.30%處于干燥位置含水率值和濕潤位置含水率值之間，且與試驗測得的整體含水率94.23%接近。這進一步驗證了本文提出的基于電導率的脫水量計算方法的適用性。

4 結 論

a.真空作用下，淤泥的脫水過程可分為主要排出液態水的快速脫水階段和主要排出氣態水的穩定促排階段，液態水和氣態水的質量比約為3∶5。

b.對于駱家溝水力沖挖淤泥，電滲脫水速率與電流呈線性關系，土體的電導率與含水率呈線性函數、指數函數或二次函數關系，其中基于線性函數關系擬合得到的電滲脫水量與模型試驗實測值之間的殘差平方和最小，相對誤差最小。

c.根據本文提出的計算方法計算得到的總脫水量所對應的淤泥理論含水率與模型試驗實測值僅相差1%，表明將真空作用和水平電滲作用下脫水量分別計算后再疊加用于估算水力沖挖淤泥脫水量是基本合理的。