基于BP神經網絡的厘米級超寬帶測距誤差改正模型設計與實驗

肖庭楊，章迪

( 武漢大學測繪學院，武漢 430079 )

0 引言

超寬帶(UWB)是一種采用極低功率譜密度和極窄脈沖寬度的無線通信和定位技術，具有穿透能力強、傳輸速率快和時間分辨率高等優點[1]，理論上可以實現cm 級的測距定位. 但由于室內環境復雜，UWB定位受多路徑等非視距誤差影響較大，這類誤差成為制約其定位精度的主要因素.

為提高UWB測距精度國內外學者展開了多方面的研究.文獻[2]引入最小二乘殘差法對粗差觀測數據進行剔除，但不能有效地處理系統誤差；文獻[3]分析了UWB非視距誤差的特性，提出了滑動窗口識別、動態調整噪聲參數的卡爾曼濾波算法進行誤差補償，但單獨改正效果不顯著，需要函數擬合等方法進行進一步改正系統性誤差；文獻[4-6]利用多項式函數、指數函數等對測距誤差進行建模，只考慮了測距誤差和測距值之間的相關性；文獻[7-10]從信號波形、信號接收強度、量測接收信號的隨機性等方面出發，利用小波神經網絡、支持向量機等機器學習方法估計測距誤差，模型較為復雜；文獻[12-14]將UWB與慣性傳感器進行組合以削弱非視距誤差的影響，需要額外的硬件支持，增加了算法復雜度；文獻[11]提出一種神經網絡改正模型，將測距值分解為兩個分量作為模型輸入但忽略了高程改正.

綜上所述，現有的UWB 誤差改正方法還存在應用范圍較窄、改正精度有限和模型過于復雜等問題.基于此，本文建立了適用于三維空間的UWB測距誤差BP神經網絡改正模型，并且分析比較了兩種不同網絡結構的模型改正效果.

1 實驗原理

1.1 BP神經網絡模型

人工神經網絡由輸入層、輸出層和至少一個隱藏層組成，每一層至少由一個神經元組成.BP神經網絡能在輸入和輸出端建立一種非線性的映射關系，算法步驟如圖1所示.

圖1 BP神經網絡算法流程圖

1.2 最小二乘定位算法

2 精度評定

2.1 測距精度評定

以測距誤差均值和均方根誤差(RMSE)評定測距精度，計算方法如式(3)、(4)所示：

2.2 定位精度評定

選取RMSE評定X、Y、Z方向定位精度，如式(5)～(7)所示：

3 實驗方案

3.1 實驗設備

實驗設備如圖2所示，UWB 設備采用DecaWave公司的DecaWavePG1.5 套件；全站儀使用Leica MS50，測角精度為1″，測距精度為0.6 mm+1×10?6.

圖2 實驗硬件設備

3.2 實驗場地

實驗地點位于8 m×12 m 的室內場地，在4個墻面上各設置1個基站，在地面設置一系列網格點，包括1 個長時間測距點、42個采樣點和5個檢核點，如圖3所示.長時間測距點用于測試測距的穩定性，采樣點用于參與BP神經網絡訓練，檢核點用于檢驗BP神經網絡效果.

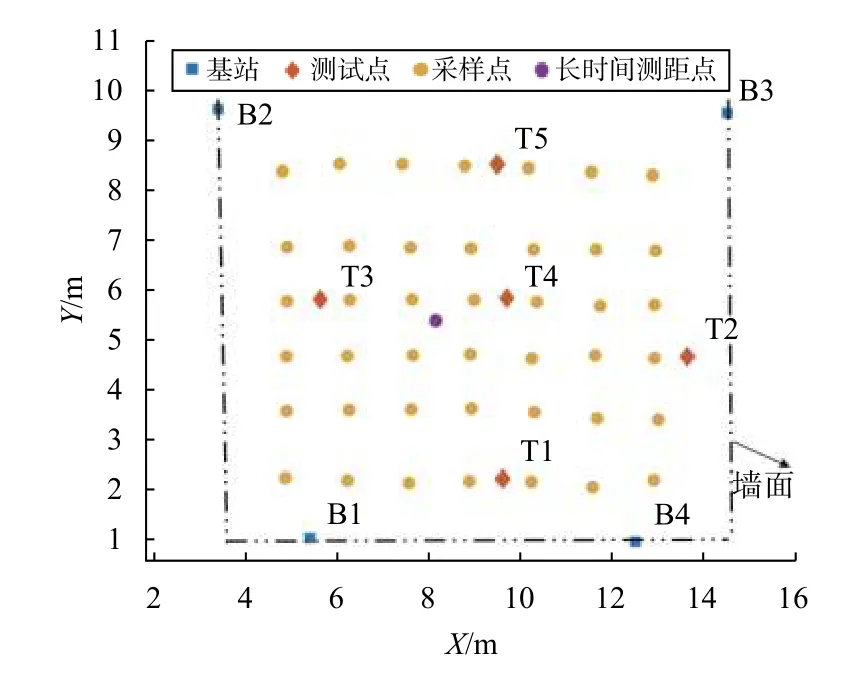
圖3 網格點分布

3.3 實驗流程

1)獲取坐標及距離參考值

利用MS50全站儀測量各UWB基站和網格點的坐標，并通過坐標反算求得標簽與各基站間距離的參考值.

2)測距穩定性測試

將UWB標簽置于長時間測距點上，進行采樣率為10 Hz、持續50 min 的數據采集，得到30 000歷元的數據，對測距穩定性進行分析.

3)網格點數據采集與測距誤差分析

利用UWB標簽對采樣點和檢核點進行逐一測量，采樣率為10 Hz、持續30 s，每點可獲得4×300=1 200個測距值；將測距值減去步驟1)中得到的參考值，對測距誤差進行統計分析.

4)網絡建模與樣本選擇

建立兩種模型：BP1 模型的輸入節點數量為4，

5)模型訓練與比較分析

將42 個采樣點上的UWB測距值和坐標分別輸入兩個模型進行訓練.5 個檢核點的數據不參與訓練，用于評價模型的測距誤差預測精度；進一步利用改正后的測距值進行定位解算，與參考坐標求差，統計定位精度.在檢驗BP2時，假定各檢核點的參考坐標未知，先利用UWB原始測距值通過最小二乘法得到檢核點的概略坐標，輸入訓練好的BP2網絡模型，分別得到其與4個基站間的測距改正值，對4個測距值均進行改正后，再進行最小二乘解算，并代入BP2模型中，重復上述過程，直至坐標變化量小于10?5.一般迭代5～8次后即可收斂.

整體實驗設計方案如圖4所示.

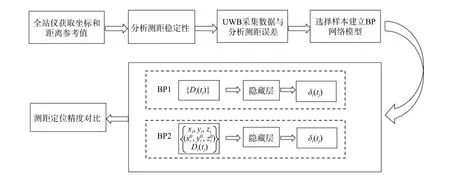
圖4 實驗流程圖

4 實驗結果

4.1 測距穩定性分析

將標簽50 min 的連續測距值與全站儀測定的距離值求差，差值序列如圖5所示，其與4個基站間距離誤差的統計信息如表1所示.由圖5可知，測距誤差較為穩定.由表1可知，標準差遠小于誤差均值，即測距誤差隨時間變化幅度遠小于測距誤差本身，因此在各采樣點上進行30 s的數據采集可以較為真實的反映其測距性能.

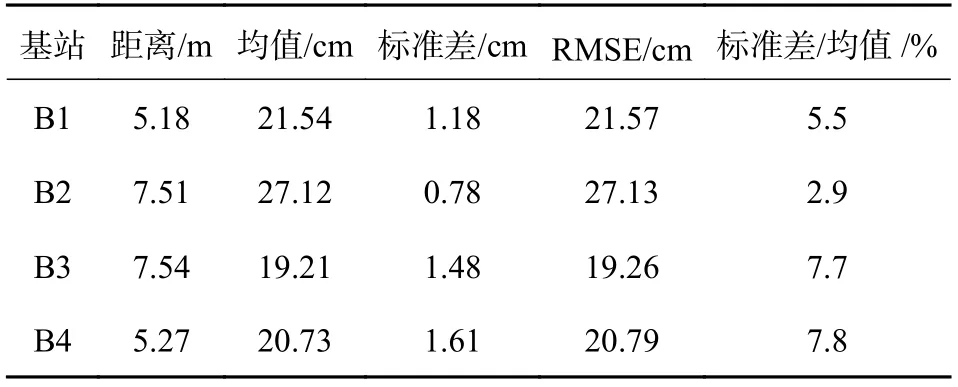
表1 長時間測距點上測距誤差統計

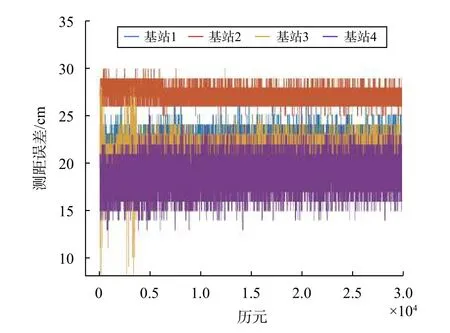
圖5 單點測距序列

4.2 測距精度分析

1)測距誤差統計

將所有網格點的距離測量值(共計42×300×4=50 400個)與全站儀測得的距離值作差，統計其均值和RMSE，結果如表2所示.

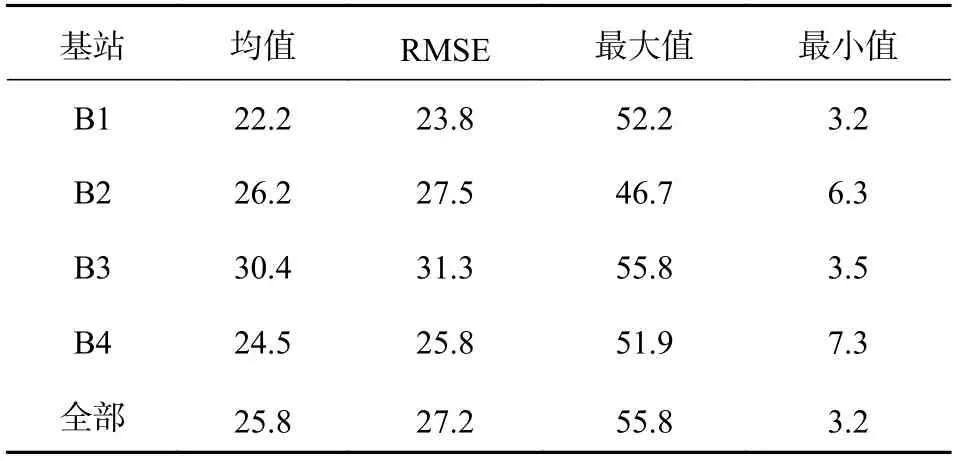
表2 測距誤差統計cm

由表2可知，實驗使用的UWB測距誤差的均值約為26 cm，RMSE值約為20～30 cm，最大可達56 cm，最小為3.2 cm，存在一定的系統性偏差，即總比參考距離要大.這主要是因為受到室內多路徑等非視距因素的影響，標簽與基站3之間的測距誤差明顯大于與其他基站間的測距誤差，這是因為基站3附近存在一較大反射面(60寸液晶電視屏)，非視距誤差偏大.

2)測距誤差與距離相關性分析

為分析測距誤差與距離之間的相關性，以網格點到基站的距離為橫軸，對應的測距誤差均值為縱軸，繪制散點圖，如圖6所示.

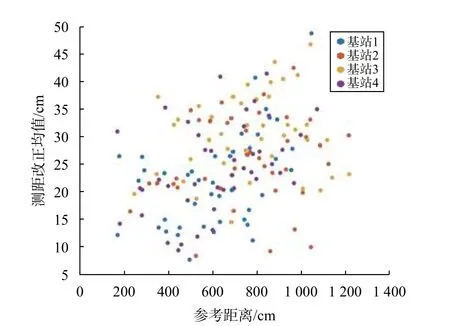
圖6 誤差-距離散點圖

由圖6中可知，測距改正值和距離之間不存在明顯的線性相關性.同一基站的測距值，距離大的誤差不一定比距離小的誤差大，反之可能更小.因此不能簡單地在測距值和誤差之間建立線性改正模型.

3)測距誤差空間相關性分析

以網格點對某一基站的測距RMSE為半徑繪制測距誤差圓，每一子圖對應一個基站，如圖7所示.

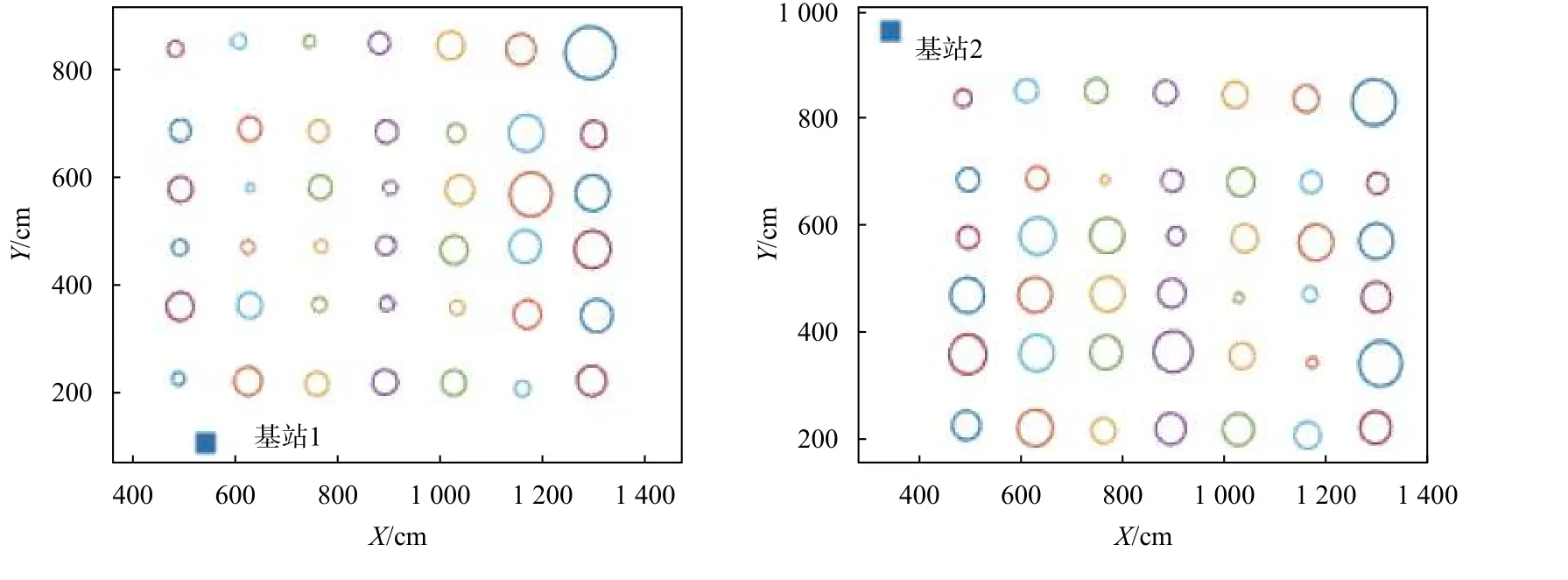
圖7 網格點測距誤差圓

由圖7可知，對同一基站，不同網格點的測距RMSE 并無明顯的空間分布規律，但不同基站間普遍呈現出一定的誤差分區現象，只是區域劃分各有不同，可見基站和網格點坐標對測距誤差均有影響，可將二者同時作為BP神經網絡的輸入，來擬合這種測距誤差的非線性分布.

4.3 BP 神經網絡對比分析

4.3.1模型訓練效果對比

模型訓練結果如表3所示.

表3 模型訓練狀態

由表3可知，BP2相關系數比BP1大0.11，更接近于1，這說明BP2有更好的擬合效果.

4.3.2測距改正精度對比

統計得到各測試點上標簽與所有基站的測距精度指標，結果如表4所示.由表4中可知經模型BP1、BP2改正后測距RMSE 明顯減小，相對于改正前，BP1平均減少83%，BP2平均減少91.7%.

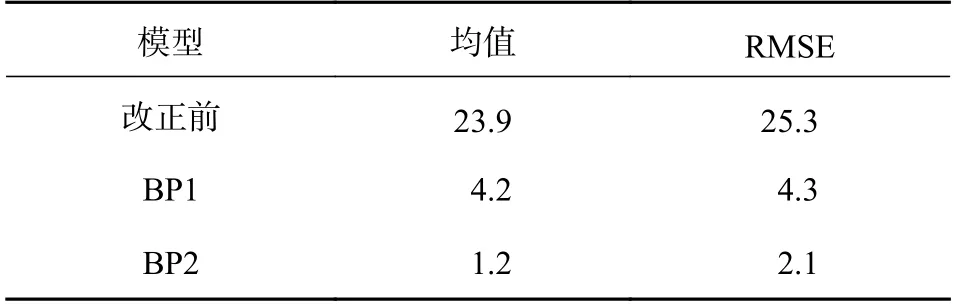
表4 測距精度cm

4.3.3定位精度對比

統計所有測試點改正前后X、Y、Z方向的定位RMSE，統計結果如表5所示.

由表5中可以知，相對于改正前的RMSE，X方向上BP1減少72.7%. BP2減少93.8%；在Y方向上BP1減少73.7%，BP2減少91.2%；在Z方向上BP1減少81.2%，BP2減少96.3%.

表5 測試點定位精度cm

以測試點T1為例，測距值經BP1、BP2改正前后，坐標散點圖分布如圖8所示，其改正后的X、Y、Z方向誤差序列如圖9所示.

圖8 測試點T1改正前后平面坐標散點圖

可以看出，進行誤差改正前，定位解算點明顯偏離參考坐標；利用BP1、BP2改正后解算點位與參考坐標間偏差均明顯減少，且BP2解算點與參考點更加接近、分布更加集中.

從圖9中可以看出在T1上，相對于BP1，BP2在Z方向精度提升幅度最大.

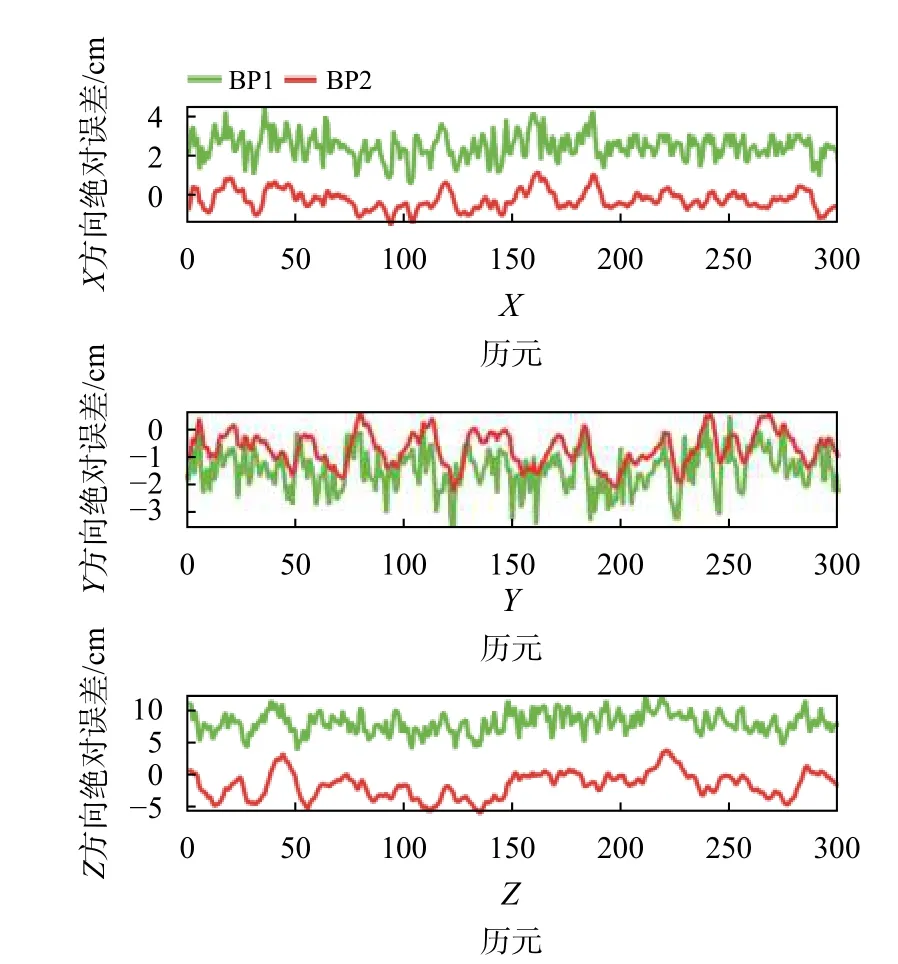
圖9 測試點T1定位誤差序列

5 結束語

UWB測距誤差是基站坐標和標簽坐標的復雜函數，難以通過常規方法建立精確改正模型.本文作者借助BP神經網絡強大的非線性擬合能力，建立了兩個不同網絡結構的誤差改正模型，以高精度全站儀測量結果作為模型訓練和對比測試的參考，實驗結果表明：兩種模型均能有效地改正測距誤差，提高定位精度.BP2模型以標簽、基站坐標作為輸入，相比以4個距離作為輸入的BP1模型，改正效果更加明顯，三個方向的定位精度均由改正前的dm 級提升至cm 級；且BP2模型的輸入不受基站數量限制，使其應用也更為靈活、適用性更強.需要注意的是，改正效果好的前提是室內環境沒有明顯變化，否則應重新進行參考值測定和模型訓練.