基于貝葉斯更新和檢測(cè)數(shù)據(jù)的服役混凝土橋梁剩余壽命預(yù)測(cè)分析
王偉芳
(廣西交科集團(tuán)有限公司,廣西 南寧 530007)
0 引言
混凝土橋梁服役過(guò)程中,在環(huán)境條件、車(chē)輛荷載以及材料退化等多重作用下,其結(jié)構(gòu)抗力不斷退化。對(duì)于沿海地區(qū)橋梁以及除冰鹽路段橋梁而言,氯離子侵蝕不可避免。隨著鋼筋表面氯離子的積累,鋼筋腐蝕過(guò)程隨之發(fā)展,不僅導(dǎo)致混凝土銹脹開(kāi)裂,引發(fā)結(jié)構(gòu)損傷,而且大大降低了橋梁的承載能力,嚴(yán)重時(shí)引發(fā)脆性破壞[1-2]。公路橋梁也受到重型運(yùn)輸車(chē)輛的沖擊,這是影響橋梁結(jié)構(gòu)可靠性的另一個(gè)主要因素。這些重載逐漸破壞結(jié)構(gòu)并加劇混凝土開(kāi)裂,使氯化物更快地腐蝕鋼筋。在普通的結(jié)構(gòu)設(shè)計(jì)中,當(dāng)施加在結(jié)構(gòu)上的載荷超過(guò)其承載力時(shí),會(huì)導(dǎo)致結(jié)構(gòu)失效。隨著結(jié)構(gòu)的老化,失效概率也隨之增加。
實(shí)際工程中橋梁的退化過(guò)程可以表示為單調(diào)遞減過(guò)程,因?yàn)槿绻贿M(jìn)行人工干預(yù)開(kāi)展維修工作,腐蝕過(guò)程和混凝土裂縫寬度的增長(zhǎng)是不可逆的。Wang和Xu[3]以逆高斯過(guò)程(Inverse Gaussian Process,IGP)為基礎(chǔ),提出結(jié)構(gòu)性能退化模型,建立了在役結(jié)構(gòu)的時(shí)變可靠度的分析框架。張建仁[4]基于結(jié)構(gòu)性能退化機(jī)理模型,考慮影響結(jié)構(gòu)性能退化各種因素的不確定性,建立了結(jié)構(gòu)抗力的隨機(jī)過(guò)程模型。
最近,隨著智能檢測(cè)技術(shù)的發(fā)展,利用已有的檢測(cè)數(shù)據(jù)得到橋梁運(yùn)營(yíng)實(shí)時(shí)狀態(tài)并對(duì)未來(lái)進(jìn)行精準(zhǔn)預(yù)測(cè)已成為橋梁安全評(píng)估的重要手段。此時(shí),貝葉斯更新方法進(jìn)入了人們的視野,與最大似然估計(jì)方法不同,貝葉斯更新不需要大量的樣本估計(jì)參數(shù),這是涉及檢測(cè)數(shù)據(jù)的理想方法[5-7]。貝葉斯方法首先根據(jù)過(guò)去經(jīng)驗(yàn)和歷史數(shù)據(jù)確定先驗(yàn)分布,當(dāng)新檢測(cè)數(shù)據(jù)可用時(shí),采用新數(shù)據(jù)更新初始分布,有效減小初始分布的不確定性。
本文以Gamma過(guò)程建模鋼筋混凝土橋梁結(jié)構(gòu)的退化,超過(guò)閾值的周期性車(chē)輛荷載根據(jù)泊松過(guò)程隨機(jī)產(chǎn)生,利用廣義Pareto分布控制超過(guò)特定臨界值的荷載,并采用貝葉斯參數(shù)更新方法結(jié)合檢測(cè)數(shù)據(jù)更新Gamma過(guò)程參數(shù)分布,以一座混凝土實(shí)橋?yàn)槔玫絽?shù)更新后的剩余服役壽命。
1 混凝土橋梁退化隨機(jī)過(guò)程
由于混凝土結(jié)構(gòu)的劣化涉及諸多因素且過(guò)程十分復(fù)雜,為簡(jiǎn)化模型,做出以下假設(shè):
(1)RC橋梁退化過(guò)程可被觀測(cè),且通過(guò)主梁抗彎承載力的降低率進(jìn)行衡量。
(2)不考慮自然災(zāi)害(如地震)的影響。
(3)將荷載視為系列脈沖,忽略其持續(xù)時(shí)間。
假定以t個(gè)時(shí)間單位表示抗力退化的隨機(jī)變量X(t)具有Gamma分布,其概率密度函數(shù)為:
(1)
其中:α(t)——形狀參數(shù),是時(shí)間的函數(shù);
β——比例參數(shù)。
Gamma過(guò)程具有以下特征:
(1)X(0)=0的概率為1。
(2)當(dāng)t1≥0,且t2>t1,增量X(t2)-X(t1)遵循分布g(α(t2)-α(t1),β)。
(3)X(t)的增量相互獨(dú)立。
由于混凝土結(jié)構(gòu)抗力的降低主要是由鋼筋的腐蝕引起的,根據(jù)文獻(xiàn)[8],線性函數(shù)α(t)=αt可用于描述鋼筋腐蝕而引起的混凝土結(jié)構(gòu)的退化。因此,結(jié)構(gòu)退化的均值和方差也為線性:
(2)
2 外荷載隨機(jī)過(guò)程
定義車(chē)輛荷載時(shí),不僅需要定義車(chē)輛荷載到達(dá)時(shí)間的分布,還需要定義荷載大小的分布。本文采用泊松過(guò)程對(duì)車(chē)輛荷載的出現(xiàn)進(jìn)行建模:
(3)
在此,t≥0,其中λ為荷載出現(xiàn)的強(qiáng)度;n為時(shí)間間隔(0,t]中經(jīng)過(guò)橋梁的荷載總數(shù)目。
根據(jù)實(shí)際交通量調(diào)查結(jié)果,不同等級(jí)或不同類型道路的荷載分布均不相同。由于重型卡車(chē)和小汽車(chē)的軸載分別分布在某個(gè)特定位置,該分布通常具有兩個(gè)峰值,因此使用幾個(gè)分布的疊加來(lái)表示軸荷分布更為準(zhǔn)確。但為簡(jiǎn)化問(wèn)題,假設(shè)只有高于某個(gè)值的載荷才能影響主梁,對(duì)于公路橋梁而言,該確定值是指主梁的自重和荷載的疊加值。因此,該荷載的值可以表示為最小載荷l0值加上超出部分。假定超出部分Y具有廣義Pareto分布,梁中相應(yīng)的最大彎矩也具有廣義的Pareto分布。廣義Pareto分布的概率密度函數(shù)和累積分布函數(shù)由式(4)、式(5)給出:
(4)
(5)
式中:a——比例參數(shù);
c——形狀參數(shù)。
3 結(jié)構(gòu)退化與荷載組合
對(duì)于橋梁結(jié)構(gòu)而言,若r0表示主梁的初始抗彎承載力,自橋梁服役以來(lái)的t時(shí)間段內(nèi)該主梁承受n次重荷載,該時(shí)間段內(nèi)主梁未失效概率即為每次車(chē)輛荷載作用于主梁但未失效概率,由此可知所用重載均低于剩余抗彎承載力概率。根據(jù)文獻(xiàn)[8]的推導(dǎo),在時(shí)間間隔(0,t]中,每個(gè)荷載的條件出現(xiàn)具有均勻分布性,概率密度為1/t。因此,主梁未失效概率表示為:
(6)
由于n個(gè)荷載獨(dú)立同分布,因此可以通過(guò)總概率定律來(lái)獲得主梁在服役壽命t時(shí)的生存函數(shù)S(t)[5]:
S(t)=P(nofailurein(0,t])
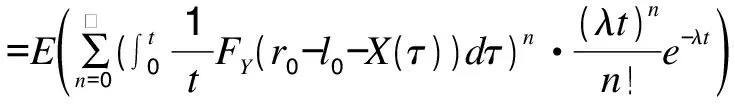
(7)
4 貝葉斯更新與剩余壽命
根據(jù)貝葉斯定理,如果假設(shè)先驗(yàn)分布,則條件獨(dú)立于給定的檢測(cè)數(shù)據(jù)集x[9]。橋梁服役壽命為結(jié)構(gòu)自身退化與交通荷載的組合,可從年度交通調(diào)查報(bào)告中查得荷載數(shù)據(jù),因此唯一需要更新的部分為橋梁退化過(guò)程,即Gamma過(guò)程。因此,如果將參數(shù)(α和β)的先驗(yàn)分布表示為π(α,β),則后驗(yàn)分布π(α,β|x)為:
(8)
在此,l(x|α,β)是給定α和β的檢測(cè)數(shù)據(jù)的似然函數(shù)。由于分母是常數(shù)值,因此后驗(yàn)分布π(α,β|x)與似然函數(shù)和先驗(yàn)密度成正比。
本文中,先驗(yàn)聯(lián)合分布π(α,β)遵循具有獨(dú)立α和β的二元正態(tài)分布。實(shí)際上,由于測(cè)量誤差始終已知且可控,因此α和β的方差可以視為恒定值,從而可得:
(9)
對(duì)于每次檢測(cè)而言,如果只能通過(guò)推斷獲得一對(duì)參數(shù)(表示為αi,βi),則后驗(yàn)聯(lián)合概率密度與先驗(yàn)聯(lián)合概率密度共軛,并且更新的參數(shù)α*和β*是先驗(yàn)值和檢測(cè)值的平均值:
(10)
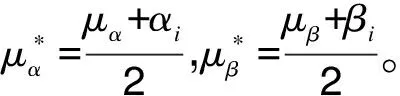
因此,如果在時(shí)刻T進(jìn)行橋梁檢測(cè),則將使用觀測(cè)到的抗力r1和具有更新參數(shù)的新Gamma過(guò)程X*(t)計(jì)算安全服役概率分布S*(t):
1-F*(t) (t>0)
(11)
以F*(t)的導(dǎo)數(shù)形式獲得橋梁安全服役密度:
(12)
此外,主梁的總壽命為時(shí)間T與檢測(cè)后的平均剩余壽命之和:
(13)
5 應(yīng)用實(shí)例
為進(jìn)一步闡述該方法,本研究以一座T形截面混凝土公路橋梁為例,主梁計(jì)算跨度為12m。主梁橫截面如圖1所示,材料特性如表1所示。當(dāng)交通荷載作用在主梁時(shí),主梁同時(shí)承受彎剪作用,最大彎矩作用于主梁跨中位置。若僅以梁的抗彎承載力為研究對(duì)象,則當(dāng)車(chē)輛荷載引起的彎矩大于該時(shí)刻主梁的剩余抗彎承載力時(shí),主梁失效。
橋梁初始運(yùn)營(yíng)時(shí)每片主梁抗彎承載力(Mcp)為4 713.25kN·m[10],鋼筋混凝土密度約為2 500kg/m3。除自重產(chǎn)生的彎矩485.1kN·m外,每片主梁的抗彎能力為4 228.15kN·m。若總重量≤17.5t(即<514.5kN·m)卡車(chē)產(chǎn)生的彎矩忽略不計(jì),則根據(jù)從交通量調(diào)查獲得的軸載譜,由交通荷載產(chǎn)生的超過(guò)514.5kN·m的部分通過(guò)廣義Pareto分布進(jìn)行擬合,其中a=0.5且c=0.02,由交通荷載引起的彎矩超過(guò)514.5kN·m的次數(shù)約為4 000次/每年。
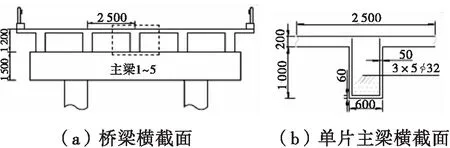
圖1 某公路橋梁橫截面示意圖(mm)

表1 混凝土主梁材料參數(shù)值表
基于同條件下類似橋梁經(jīng)驗(yàn)數(shù)據(jù),彎矩退化率平均值為9.78kN·m/年,相應(yīng)的方差為6.5。因此,Gamma過(guò)程分布的參數(shù)為α=14.715和β=1.505。表2列出了Gamma過(guò)程分布參數(shù)的先驗(yàn)聯(lián)合正態(tài)分布,基于式(7),利用蒙特卡羅方法得到服役壽命的先驗(yàn)概率密度函數(shù)。
橋梁服役運(yùn)行10年后,通過(guò)檢測(cè)主梁的鋼筋直徑,得到抗彎承載力為4 550kN·m,抗彎承載力退化率為16.84kN·m/年,相應(yīng)的方差為8.8。因此,相應(yīng)的α和β值分別等于32.226和1.914。此外,新的交通調(diào)查顯示,因交通荷載產(chǎn)生的彎矩超過(guò)514.5kN·m的次數(shù)約為5 000次/每年。基于貝葉斯更新,得到后驗(yàn)概率分布(見(jiàn)表2)。另外,通過(guò)蒙特卡洛方法計(jì)算得到相應(yīng)的服役壽命后驗(yàn)分布。
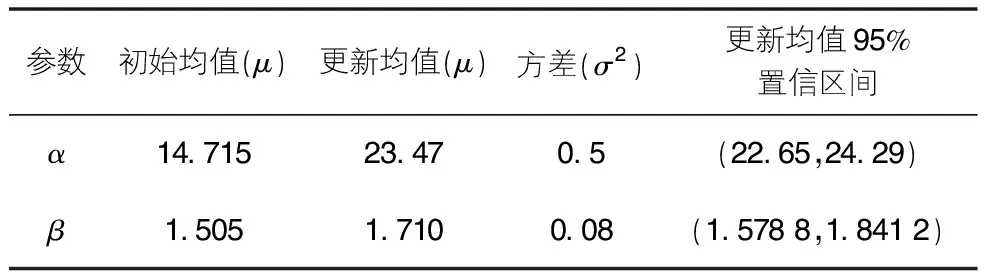
表2 先驗(yàn)與后驗(yàn)參數(shù)比較表
如下頁(yè)圖2所示給出了第10年檢測(cè)后主梁的剩余服役壽命的先驗(yàn)和后驗(yàn)累積分布函數(shù)與概率密度函數(shù)的比較。結(jié)果發(fā)現(xiàn),該橋梁退化速度明顯快于初始預(yù)期,這可能是由于十年來(lái)交通量增長(zhǎng)和重載車(chē)輛增加所致,在現(xiàn)有服役的公路橋梁中,該現(xiàn)象非常普遍。因此,在橋梁的實(shí)際運(yùn)行中,一旦出現(xiàn)這種情況,應(yīng)及時(shí)修訂維護(hù)計(jì)劃,以確保在更新后的退化速率下橋梁正常運(yùn)營(yíng)。
另外,通過(guò)利用橋梁檢測(cè)數(shù)據(jù)對(duì)Gamma過(guò)程的參數(shù)進(jìn)行更新,可以大大減小主梁剩余服役壽命的標(biāo)準(zhǔn)差,從而減小其不確定性,提高預(yù)測(cè)精度,這進(jìn)一步體現(xiàn)了收集檢測(cè)數(shù)據(jù)進(jìn)行貝葉斯更新的重要性。
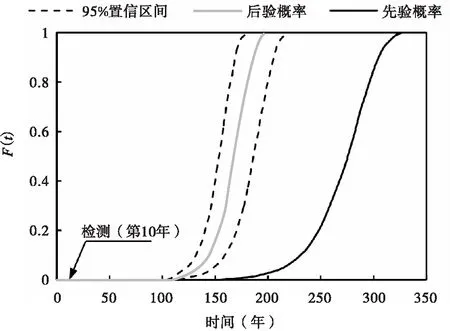
(a)累計(jì)分布函數(shù)(CDF)
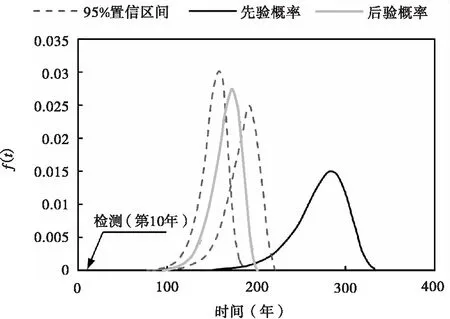
(b)概率密度函數(shù)(PDF)
6 結(jié)語(yǔ)
本文將車(chē)輛載荷與混凝土的退化過(guò)程相結(jié)合,通過(guò)貝葉斯更新方法得到了服役橋梁的剩余壽命。針對(duì)直接更新壽命分布十分困難的問(wèn)題,將混凝土退化過(guò)程建模為Gamma過(guò)程,將車(chē)輛荷載建模為泊松過(guò)程,并采用廣義Pareto分布控制隨機(jī)荷載的變異性,進(jìn)一步提出抗力-荷載效應(yīng)雙隨機(jī)過(guò)程的服役橋梁剩余壽命評(píng)估方法。基于橋梁檢測(cè)信息,利用貝葉斯方法更新Gamma過(guò)程的參數(shù),采用蒙特卡羅方法計(jì)算橋梁剩余服役壽命的累積分布函數(shù)和概率密度函數(shù)。本研究可有效利用檢測(cè)數(shù)據(jù)為橋梁安全維護(hù)提供理論依據(jù)。

