量子優化算法綜述

何鍵浩 李綠周

(中山大學計算機學院 廣州 510006)

優化(optimization)是計算機科學與數學領域十分重要的基礎研究之一，同時也是機器學習的核心工具[1].相關理論與方法廣泛應用于各類工業生產[2]、工程設計與管理[3-5]、交通運輸[6]、經濟決策[7]、市場管理[8]等關乎國計民生的重要領域.一個具體的優化問題由3個基本要素組成：1)目標函數(或損失函數)，即決策者需要優化的指標，如總消耗、總收益等，數學形式表現為由優化變量到指標的函數/映射.2)優化變量，即決策者可以調整且會影響到目標函數的變量，如產品工藝、資金分配等.3)約束條件，即在決策過程中必須遵守的限制，如安全標準、資源儲備總量等.優化過程就是在約束條件的限制下，尋找能最小化或最大化目標函數的優化變量的賦值.優化有時候也被稱為數學規劃，下文中優化與規劃意義等價，具體使用的詞匯將根據該細分方向的用詞習慣決定.

根據優化問題的變量是否連續，優化技術可以分為離散變量優化(也稱為組合優化)和連續變量優化兩大類.其中，根據目標函數是否是凸的，連續變量優化又可分為凸優化和非凸優化.凸優化主要研究的是目標函數為凸函數且優化變量可行域為凸集的優化問題，由于凸集凸函數有許多優秀的性質(例如極小值即最小值)，使得凸優化問題有很多高效的解法，在應用迭代方法求解時也能獲得良好的收斂速度.因此，凸優化技術方面已有成體系的方法且有廣泛的應用.相對而言，非凸優化還有很大的發展空間.另外，許多非凸優化問題，目前有效的辦法仍然是轉化為凸優化問題求解.

與此同時，自從Shor快速整數分解量子算法[9]、Grover量子搜索算法[10]以及HHL量子解線性方程算法[11]的提出，量子計算就因其與生俱來的并行性而受到廣泛關注，近年來量子計算理論方面的研究進展可參考文獻[12-13].因此，如何利用量子計算技術來加速優化問題的求解、提高優化效果成為受關注的問題，逐漸形成了量子優化這一研究方向.量子優化算法的研究從時間上大致分為1996—2015年和2015—2021年這2個階段.

1)1996—2015年.此階段的量子優化算法主要是針對離散變量優化問題而設計，且有較多的啟發式算法.此階段的量子算法主要得益于當時3類基礎離散量子技術：

① Grover算法以及量子隨機游走.這2個基礎算法后續還有不少改進與擴展，多被用于加速搜索過程.

② 量子退火法.量子退火法無需使用糾纏態，實現較簡單，因此已經有了D-Wave這樣的大型專用量子計算機可供實驗研究.

③ 量子近似優化技術.量子近似優化算法雖然還沒有關于理論優勢的嚴格分析，但被認為適合近期的含噪中等規模量子(noisy intermediate-scale quantum,NISQ)計算設備，因此得到不少關注.

2)2015—2021年.此階段的量子優化算法主要針對連續變量優化問題而設計.連續變量優化問題的解法以迭代算法為主，迭代開銷以及收斂速度是影響算法效率的主要因素.此階段的量子算法主要得益于4類量子技術的發展：

① 解線性方程量子算法的設計思想.此類方法可用于加速與矩陣操作相關問題的求解.

② 哈密頓模擬技術.此類方法的發展為量子態演化提供了高效的實現方案.

③ 量子隨機存儲器.借助量子隨機存儲技術對數據進行預處理，可以使算法的效率得到提升，不過量子隨機存儲的搭建仍然需要進一步的優化來保證整體的優勢.

④ 量子梯度估計法.計算梯度是許多優化問題的核心步驟，量子梯度估計法的提出為此提供了便利.

連續變量量子優化算法是近年的研究趨勢，研究內容涵蓋了優化領域中梯度下降、牛頓法、內點法等常用的傳統迭代方法，也有針對具體優化問題的持續研究，因此本文將重點介紹連續變量量子優化算法，該方向的研究目前主要集中在量子凸優化方面.

1 基本量子算法簡介

本節介紹在量子優化算法中使用頻率較高的基本量子算法/技術.關于量子計算的基本知識以及更全面的介紹可參考文獻[14-16].本節主要介紹一些相對底層的核心算法/技術，它們最初設計時并不是為了優化算法，可廣泛應用于不同的領域，其中當然也包括優化領域.

1.1 Grover算法與量子隨機游走(Grover algorithm &quantum random walk)

Grover算法與量子隨機游走已經被應用在許多領域，其中就有離散優化領域.Grover算法于1996年被提出[10]，用于無序數據庫搜索，其方法是通過迭代利用一個可識別搜索目標的黑盒來提高搜索目標在量子疊加態中的振幅，從而提高測量獲得搜索目標的概率.后續有多個相關的改進結果，如由清華大學的Long提出的Grover算法的精確版本[17].原始的Grover算法需要確切知道搜索空間中目標的數量才能確定最優的迭代次數，過少的迭代次數達不到效果，過多的迭代也會降低搜索的成功率，迭代次數增多并不能保證一直趨向搜索目標.該問題在文獻[18]中被稱為“soufflé problem”.因此，對于搜索空間中目標數量未知的情形，算法需要改進，Grover和Mizel先后對此作過討論，并給出了隨著迭代次數增加能一直增加搜索成功率的改進版本[19-21]，但這幾項工作都一定程度上犧牲了算法效率.最終Yoder等人給出了進一步改進[22]，既保留了平方加速，也保證了迭代最終會一直趨向搜索目標.此系列改進工作被稱為固定點量子搜索(fixed-point quantum search).若搜索前對答案有一定的先驗知識，He等人給出了相應最優算法[23].

量子隨機游走于1993年由新墨西哥大學的Aharonov等3名學者提出[24].不同時期量子隨機游走的工作梳理可參見文獻[25-28].Grover算法可以看作是在一種特殊圖上的量子隨機游走，因此量子隨機游走是一種更一般化的量子搜索技術，已經成為一類重要的量子算法設計模型.

1.2 量子傅里葉變換與量子相位估計算法(quantum Fourier transform &quantum phase estimation algorithm)

作為量子算法里提供加速的最為核心的2個基本工具，量子傅里葉變換最早可追溯到1994年[29]，而量子相位估計算法最早可追溯到1995年[30].利用量子解線性方程思想以及量子梯度估計法的量子優化算法都直接或間接地使用了量子傅里葉變換或量子相位估計算法.讀者可以在任一量子計算教材中找到這2個基本工具的詳細介紹[14-16].

1.3 量子幅值放大/幅值估計(quantum amplitude amp-lification and amplitude estimation)

2002年，Brassard等4名學者提出了量子振幅放大以及量子振幅估計算法[31].前者通過一系列的反射操作，達到放大所需結果概率的目的;而后者則是在前者的基礎上結合量子相位估計算法，從而估計所需結果的概率.在量子優化算法中，不完美的演化產生的垃圾信息，以及算法本身產生的無用信息一般都通過振幅放大過濾掉.該工作與Grover算法[10]以及量子計數[32]有密切聯系.Ambainis于2012年提出了量子振幅放大算法的時變版本[33]，并用于求解線性代數問題.量子振幅估計算法近期還有針對非布爾函數的推廣[34]以及無需使用量子相位估計算法的變種[35].

1.4 解線性方程量子算法(quantum linear system algorithm)

解線性方程量子算法最早在2009年由Harrow，Hassidim，Lloyd三名學者提出[11]，所以也被稱為HHL算法.解線性方程即給定矩陣A與向量b，求滿足Ax=b的x.此類算法也可以用來處理矩陣與向量乘積、矩陣求逆等操作，因此也常見于量子優化技術的迭代算法中.需要注意的是，解線性方程量子算法求解的是量子版本的問題，即輸入輸出均為量子態，無法直接得到解的每一個分量，因此在進一步應用時需要經過巧妙設計，一般在利用方程解的全局信息時才能體現量子算法的加速效果.Ambainis于次年提出了改進版本，減少了算法復雜度對矩陣條件數的依賴[36].2017年，Childs等3名學者用其他思路給出了解線性方程量子算法[37]，減少了計算復雜度中對精度的依賴.2018年，Wossnig等3名學者利用量子奇異值估計算法，去除了計算復雜度中對矩陣稀疏度的依賴[38].關于此系列工作的梳理可以參見文獻[39].

1.5 量子隨機存取存儲(quantum random access memory)

要在經典問題上使用量子算法，經典數據編碼成量子態是必不可少的重要步驟，量子隨機存取存儲(簡稱QRAM)則是這一過程的主要輔助技術.同為實現數據的存儲和提取，QRAM與經典的隨機存儲器最大的區別是：QRAM可以被量子疊加態地址訪問，返回與地址相糾纏的疊加態數據，這為量子優化算法以及量子機器學習的初態制備提供了有力工具.在量子優化中使用得較多的為2008年Lloyd等3名學者提出的Bucket-Brigade結構的QRAM[40-41]，利用此結構在對數時間復雜度內可實現初態制備.值得注意的是搭建QRAM的時間復雜性仍然較高，整體上會抵消掉量子算法帶來的加速，QRAM搭建技術仍然需要進一步優化.2018年，Chakraborty等3名學者提出了塊編碼技術，并證明與Bucket-Brigade結構在矩陣編碼上等價[42].

1.6 哈密頓量模擬(Hamiltonian simulation)

哈密頓量是與量子系統總能量有關的運算符，根據薛定諤方程可知，它可用于描述量子系統隨時間的演化，通過操作哈密頓量可以實現量子態的演化.在部分量子優化算法中(特別是用到解線性方程量子算法思想的算法)，矩陣被編碼成哈密頓量的形式，進而作用到量子態上.哈密頓量模擬就是尋找能高效逼近目標哈密頓演化的酉演化，從而在有效時間內完成演化(亦即實現了量子算法的過程).關于哈密頓量模擬的正式結果最早可追溯到1996年Lloyd發表在《Science》上的文章[43]，并隨后被推廣到稀疏哈密頓量的模擬上[44-45]，且效率得到逐步提升[46-49].以上的工作針對的都是時間無關哈密頓量，而其后還有針對時間相關哈密頓量的推廣工作[50-51].除研究時間復雜度與查詢復雜度外，近年也出現了研究哈密頓量模擬采樣復雜度的工作[52].

2 離散變量量子優化技術

本節簡要介紹離散變量量子優化技術.主要離散變量量子優化技術的提出時間距今較長，因此本節只簡單介紹各技術的歷史以及給出重要工作的引文供讀者進一步了解.

2.1 基于Grover算法與量子隨機游走的優化算法(optimization based on Grover algorithm &quantum random walk)

經典離散優化的算法往往離不開搜索，而Grover算法與量子隨機游走則正是加速搜索的量子算法，因此十分適合用于加速離散優化問題的求解.用Grover算法解決的離散優化問題有：無序數據最小值尋找[53]、最小生成樹與最短路問題[54]、最大整數網絡流查找[55]等.作為Grover算法推廣的振幅放大算法也有相應的離散優化應用[56].量子隨機游走則被用于加速基于Markov鏈的技術[57]等.近年也有用連續時間量子隨機游走解決組合優化問題的工作[58].

2.2 量子退火/量子隨機優化(quantum annealing/quantum stochastic optimization)

量子退火法于1989年由比勒費爾德大學的Carvalho等3位學者提出[59]，也稱為量子隨機優化.如遺傳算法、蟻群算法與模擬退火等仿生算法都是非常實用的啟發式優化技術，其中模擬退火法是出現得較早的經典技術，研究較深入.1)量子退火法中使用隧道場強度作為經典模擬退火法的溫度參數.由于量子隧穿效應的存在，使得量子退火法更容易跳出局部最優解，獲得全局最優解，從而體現出超越經典模擬退火的優勢.2)量子退火不需要運用量子糾纏，因此易于實現，D-Wave公司生產的專用量子計算機即可運行量子退火算法.關于量子退火的早期工作可參閱文獻[60-61]，關于D-Wave計算機與量子退火的綜合介紹可參閱文獻[62].

2.3 量子近似優化算法(quantum approximate optimization algorithm)

一般我們說的量子近似優化算法，都習慣特指本節所述的求解組合優化問題的量子近似優化算法，關于該算法的入門介紹可參照文獻[63-64].

量子近似優化算法(簡稱QAOA)于2014年由麻省理工學院的Farhi等3位學者提出[65]，最初的設計是用于求解組合優化問題.該工作的量子電路深度依賴于一個與精度有關的參數，最壞情況下電路深度隨著該參數與約束條件數量的乘積呈線性增長.該工作給出了使用QAOA解決p-正則圖最大割(Max-Cut)問題的例子(p≤3)，而傳統做法是把最大割問題轉化為圓錐線性優化問題(conic linear optimization problem)解決.相較于經典算法，初期的QAOA并沒有顯示出明顯的優勢，直到2016年麻省理工學院的Harrow等2名學者指出QAOA是實現量子霸權(quantum supremacy)的方法之一[66]，熱度才有所上升，近年也有理論分析的嘗試[67].另一方面，QAOA算法實現時對相干時長要求低，或許是現有的小規模量子計算機理想的實驗內容之一，因此受到了量子計算實驗研究者的關注，陸續有實驗文章出現[68].另外，近年也出現了用QAOA算法解決連續優化問題的研究，見3.5節.

3 連續變量量子優化技術

本節將詳細介紹連續變量量子優化技術.連續變量量子優化技術是近5年的研究熱點，因此本節將詳細給出各工作所針對的具體問題、算法復雜度，以及所采用技術的直觀描述.對于與經典模型有關的量子算法，本文還會給出該經典模型的框架介紹以便讀者理解.問題和模型都將列在方框內.

3.1 量子梯度估計法(quantum gradient estimation)

在許多優化方法中，特別是迭代方法的梯度下降法與牛頓法，都需要目標函數的梯度信息，因此梯度估計是這類方法的核心技術之一.量子梯度估計法于2005年由麻省理工學院的Jordan提出[69].

梯度估計問題(查詢模型)：

給定：函數f:Rd→R的查詢黑盒Of(查詢返回詢問點的函數值)，點x=(x1,x2,…,xd)∈d.

該工作研究的是查詢模型，在給定目標函數黑盒的情況下，量子梯度估計算法只需要調用O(1)次查詢黑盒，即可近似計算出目標函數在某點的梯度，與優化變量的維度無關.當目標函數估值較困難、優化變量維度較大時，量子梯度估計法有一定的優勢.美中不足的是，該算法無法通過遞歸求解目標函數的高階導數，求n階導數需要額外的2n次查詢來計算所需要的相位信息，因而失去了量子優勢.此工作主要使用了量子相位估計技術.2019年，來自荷蘭國家數學與計算機中心與微軟研究院的研究人員合作改進了量子梯度估計法[70]，并指出原有的量子梯度估計法采取的黑盒輸入模型過強，實際上難以達到所需精度，因此改而研究相位黑盒輸入模型與概率輸入模型，并給出了這2種輸入模型的轉化關系.在該輸入模型下，改進算法估計平滑函數的梯度時在查詢復雜度上有二次(quadratic)加速，并且證明了量子優化產生的大多數目標函數會滿足必要的平滑條件.

3.2 量子梯度下降法(quantum gradient descent)

迭代方法在無閉式解的優化問題中有非常廣泛的應用，梯度下降法就是其中一種迭代方法.梯度下降法從初始的、未經優化的解開始，每輪根據與目標函數的梯度有關的更新規則迭代更新解.由于梯度方向是函數增長速度最快的方向，梯度的反方向是函數下降速度最快的方向，因此參照梯度信息進行迭代，能更快地獲得滿足要求的近似最優解.

由于量子計算的特性，運用迭代方法時一旦其中一步失敗，輸入就損毀了，一切就要重頭再來，這使得若要達到迭代τ次的效果，往往需要遠多于τ次實現迭代操作的量子演化.

梯度下降法：

猜測初始解θ0；

針對單位范數(unit norm)約束多項式優化(polynomial optimization)的量子梯度下降法于2019年由MIT的Lloyd等學者提出[71].該方法對數據維度較大的情況有優勢，且把量子計算技術推進到了非二次優化甚至非凸優化問題上.

多項式優化(帶單位范數約束)問題：

給定：N2p個系數Ai1…i2p∈，其中p為正整數.

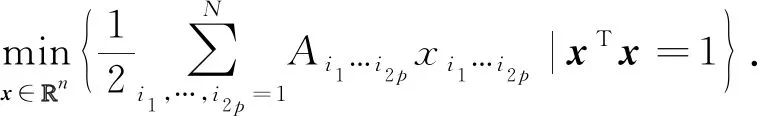
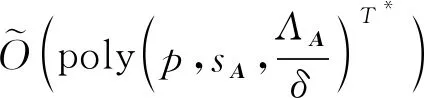
二次優化問題：

給定：A∈n×n,b∈n,c∈.

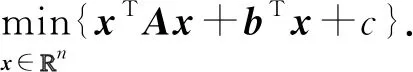
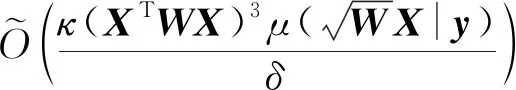
帶權最小二乘問題：

給定：樣例矩陣X、對應的標簽向量y以及權重向量w.

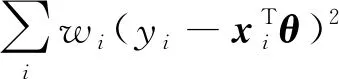
此工作運用的技術為量子奇異值估計算法(包含了量子振幅放大、量子振幅估計以及量子相位估計算法).該工作在原有QRAM的算法設計模型上作了一些改進，使得量子奇異值估計算法的時間復雜度由原來的與待分解矩陣的F范數有關，改進為與最大行范數與F范數兩者之間的較小者有關.由于有不少現實問題待分解的矩陣的行范數都是有界的(boundedl1norm)，這一改進是有應用價值的，而且該改進也可以運用在量子解線性方程上.

3.3 量子在線梯度下降(quantum online gradient descent)

在線凸優化是在線學習中的一個重要的框架，是凸優化與博弈論的交叉領域，在決策問題中有非常廣泛的應用，如在線路由問題、投資組合問題以及推薦系統等，都可以用在線凸優化的框架建模，并用相關技術解決.

在線凸優化模型：

給定凸集K?n，凸函數族F:n→.

決策者依序進行T*輪決策，在第t∈{1,2,…,T*}輪時：

1)在凸集K中做出決策xt;

2)遭受損失ft(xt)，其中ft∈F由對手選取或者由環境生成;

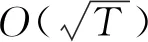
3.4 量子牛頓法(quantum Newton’s method)

牛頓法是一種處理無約束優化問題的迭代方法，相比每次迭代沿著梯度方向移動的梯度下降法，牛頓法把曲率也考慮在內，因此往往能加快收斂速度.梯度下降法與牛頓法之間是迭代復雜度與迭代次數之間的相互轉化，每次迭代考慮更多信息的牛頓法自然單次迭代計算復雜度會更高，但由于收斂更快，因此迭代次數相應下降.2種方法不能簡單說孰優孰劣，各有不同的適應場景.

牛頓法：

猜測解θ0；

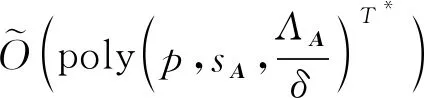
3.5 連續變量量子近似優化算法(quantum app-roximate optimization algorithm for continuous variable)

針對連續優化問題的量子近似優化算法于2019年由滑鐵盧大學的Killoran等學者提出[74].該工作參考了離散版本QAOA的思路，并用量子粒子勢能動力學(quantum dynamics of particles in energy potentials)的技術編碼目標函數.該算法適用于有約束與無約束優化，稍加修改也可以解決離散優化問題.文章作者給出了使用此算法最小化非凸Styblinski-Tang函數的數值模擬實驗.

同樣地，該工作相對現存經典技術的優勢仍待進一步論證，且此版本的實現難度要比離散版本高，超出了目前量子計算機可實驗的范圍.

3.6 量子內點法(quantum interior point method)

內點法是處理有約束優化問題的迭代方法之一，常用于線性規劃與二次規劃，實際應用面與著名的單純形法分庭抗禮，而且相較于非多項式算法的單純形法，內點法是多項式算法，因此在大規模的線性規劃問題中有更大的用武之地.

內點法：

松弛變量，把待優化問題的不等式約束條件轉化為線性不等式約束；

目標函數中引入不等式約束條件的屏障函數(barrier function)，構造中央路徑(central path)函數；

用牛頓法沿著中央路徑尋找最優解.

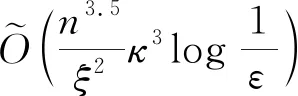
在內點法中，計算牛頓線性系統矩陣(Newton linear system matrix)是非常花時間的，而該文提出了構造牛頓線性系統矩陣塊編碼的量子技術，加速了這一過程，主要運用的是量子態層析技術.該文作者同時證明了算法的收斂速度與經典方法一致，因此量子內點法所需的迭代次數與經典算法一致.綜合每次迭代的加速而言，量子內點法是一個理論突破.

2019年，文獻[75]的2名學者與Szilágyi合作先后發表3篇文章，分別把量子內點法擴展到解決二階錐規劃[76]，以及應用到投資組合問題[77]與支持向量機[78]上.

二階錐規劃問題:給定:A(i)∈RRm×ni,ci∈RRni,i∈[r],b∈RRm.求:minx1,…,xr{∑ri=1cTixi∑ri=1A(i)xi=b,xi∈Lni},其中Lni=x=x0;x～ ∈RRni x～≤x0}為洛倫茲錐(Lorentz cones),?i=[r]. 投資組合問題:投資者需要對m只投資產品的資金分配做T輪決策,每輪結算后根據之前的投資決策進行下一輪的分配計劃,最終目的是使得總收益最大化.

3.7 量子半正定規劃(quantum semi-definite pro-gramming)

半正定規劃是凸優化問題的一個分支，針對的是目標函數為線性函數、優化變量約束在光譜面上(半正定矩陣構成的錐體與仿射空間的交集)的優化問題，存在多項式時間的經典算法.由于半正定規劃在現實中應用面廣，輸入規模大，因此多項式時間仍然不能滿足發展需要.2017—2019年，量子半正定規劃法經過了多次迭代，并得到了快速發展.

半正定規劃問題(原始形式):給定:A1,A2,…,Am,C∈RRn×n,b1,b2,…,bm∈RR.求:max{tr(CX)|?j∈[m],tr(AjX)≤bj,X≥0}. 半正定規劃問題(對偶形式):給定:A1,A2,…,Am,C∈RRn×n,b∈RRm.求:miny∈RRm{bTx|∑k∈[m]ykAk≥C}.

量子半正定規劃方法于2017年由加州理工學院的Brand?o與微軟研究院的Svore提出[79]，該算法比經典算法有著關于矩陣維度的平方級加速，且當矩陣越稀疏，優勢越明顯.量子吉布斯采樣(quantum Gibbs sampling)與乘權法(the multiplicative weight method)是實現該算法的關鍵技術.

文獻[79]的作者還與馬里蘭大學的研究人員合作，針對設備帶誤差的情況進一步優化了量子半正定規劃算法[80]，使得上界進一步逼近下界.與文獻[79]不同的是，該算法使用的是量子態輸入模型直接獲得純化的混合態，且采取的是零和游戲框架.該文核心技術是用快速放大算法(fast amplification algorithm)改進了量子OR引理，提高了算法速度.

van Apeldoorn等4名學者提出了對文獻[79]的改進[81]，降低了精度對算法上界的影響，并給出了所有線性規劃算法的量子查詢下界(因此包括了所有的半正定規劃算法)，該工作還把他們的改進版本應用在了實現給定哈密頓量平滑函數與函數廣義最小值查找算法上.

2018年，van Apeldoorn等2名學者綜合以上的幾項工作的優點以及Gentle Quantum Search引理，提出了量子半正定規劃的改進版本[82].該工作給出了更優的上下界，分別論證了在量子態輸入、稀疏矩陣輸入以及量子算子輸入這3種不同輸入模型下的算法效率，并應用到陰影層析問題、量子態區分問題以及E-最優設計上.

這4項工作的復雜度上下界詳見表1.

Table 1 Main Results of Quantum Semi-Definite Programming表1 主要量子半正定規劃結果

需要注意的是，精度等參數對于量子半正定規劃計算復雜度的影響仍然較大，因此要在實際問題上超越經典算法依然需要進一步的研究.

3.8 量子線性規劃(quantum linear programming)

線性規劃是半正定規劃的一個特殊形式，從實用的角度比更一般的半正定規劃應用更為廣泛.除了3.6節提到的可用于解線性規劃問題的內點法外，還有2項針對線性規劃問題的量子工作.

線性規劃問題(原始形式):給定:A∈RRn×m,b∈RRn,c∈RRm.求:minx∈RRm{cTx|Ax≥b,x≥0}. 線性規劃問題(對偶形式):給定:A∈RRn×m,b∈RRn,c∈RRm.求:maxy∈RRn{bTy|ATy≤c,y≥0}.

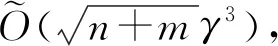
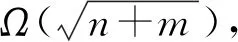
3.9 一般凸優化的量子算法(quantum algorithm for general convex optimization)

針對一般的無約束凸優化問題，馬里蘭大學的Childs團隊[85]與荷蘭國家數學與計算機中心de Wolf團隊[86]于2020年分別獨立地提出了相應的量子算法.

一般凸優化問題(查詢模型)：

給定：凸集K?n的成員黑盒OK(查詢返回詢問點是否在集合內)，凸函數f:K→的估值黑盒Of(查詢返回詢問點的函數值).

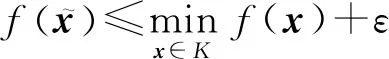
文獻[85-86]的2項工作結論一致，研究的均為黑盒查詢模型，思路大致類似.在給定成員黑盒(用于查詢優化變量給定取值是否在可行域中)與估值黑盒(用于計算目標函數在給定點的值)情況下，2項工作的結果由表2說明.我們可以從表中看到，在時間復雜度相同的情況下，量子算法的查詢上界達到了經典算法的下界，這意味著該量子算法在理論上達到了經典算法潛在的最好情況.另外，量子算法上下界仍然未緊，這意味著量子算法仍然有提升空間.由于2項工作結論一致，以下主要介紹文獻[85]的技術.

Table 2 Comparison of Quantum and Classical General Convex Optimization Algorithms表2 量子與經典一般凸優化算法的對比

針對一般凸優化問題的量子算法使用的主要是量子梯度估計技術，從估值黑盒出發通過量子梯度估計求得分離超平面，經由分離超平面再得出最小化線性函數的方法，最后得出一般凸優化問題的算法，這過程中綜合運用工程中常見的誤差縮小技術與函數緩和技術處理邊界不光滑等會影響算法性能與誤差的問題.

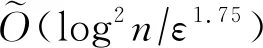
4 總 結

優化問題在生產生活中無處不在，經典計算領域把優化作為一個正式的學科分支進行研究已經有一百多年的歷史，而最優化方法的起源甚至可以追溯到三四百年前費馬、拉格朗日、牛頓以及高斯的微積分時代.隨后經歷了高度依賴一階、高階導數的分析算法階段、用準確度交換速度的啟發式算法階段，以及高度依賴數據的代理模型階段.如今在工程實踐中，各類方法高度融合，產生著巨大的經濟社會效益.

但縱使已經研究了數百年，在優化領域還一直有許多難題尚未得到有效的解決，有如大部分的非凸優化問題、組合優化里的NP問題，以及許多規模極大的P問題，都還處于探索階段.而量子計算的興起為這些難題帶來了新的希望和探索方向.量子算法已經在不少問題上相對于經典算法帶來了加速優勢，但由于中等規模量子計算機目前依然昂貴，大型的通用量子計算機難見蹤跡，因此量子優化算法的設計目前依然處于理論分析難、實驗成本高的階段，學術界與工業界都迫切盼望量子計算能在基礎理論與軟硬件技術上有進一步的突破.

本文通過對量子優化算法研究方面的梳理觀察得出4方面：

1)從時間上看，連續變量的量子優化算法是近年的趨勢，也將會是未來短期內的研究熱點.這并非說組合優化不重要，而是組合優化問題有很大一部分是NP問題，要找到高效的量子算法具有挑戰性.已有的針對組合優化問題的量子算法要么是采用Grover算法，在某個子過程達到根號級別加速，要么就是采用無法在理論上分析復雜度的啟發式算法，而目前的量子計算機規模還不足以驗證啟發式量子算法的應用價值.連續變量優化問題似乎更有希望獲得更多的量子加速，而且其應用面也因人工智能的發展而日益廣泛.

2)量子優化使用的基本量子技術的核心思想大多都是1995—2008年提出的，HHL算法以及Jordan量子梯度估計法均為1995年相位估計算法框架的延展，幅值放大技術為1996年Grover算法的延展，而哈密頓量模擬算法以及量子隨機存儲技術也已有10～20年的歷史.若需要尋找新的方向，還需要在最為底層的算法上有突破.

3)除啟發式算法外，主要的量子優化算法相對于經典算法都在理論上體現了一定的加速，既有體現在時間復雜度的加速，也有體現在查詢復雜度上的加速.一般來說，問題的計算復雜度下界往往很難證明，但查詢復雜度的下界證明有如對手法[89]等較成體系的方法.縱觀現有工作，在一般凸優化問題的查詢模型上[85-86]尋找量子優勢是很有希望的，因為其量子上界已經達到經典下界，且量子上下界還未緊，還有改進空間.

4)目前獲得量子加速的優化問題十分有限，優化領域依然存在許多值得量子計算科學家探索的問題，如優化領域的難題：非凸優化.對凸優化研究的深入是經典優化領域的一個分水嶺[90]，因為凸函數具有極小值即最小值等良好特性，使得凸優化問題大多都有可行、高效的算法，因此凸優化問題與能轉化成凸優化問題的優化問題被認為是較易解決的.相對地，解決非凸優化則比較困難.現在的量子優化算法中，針對的線性規劃、二次規劃、半正定規劃問題都是常見的特殊凸優化問題，都屬于經典優化領域認為較易解決的部分，針對非凸優化的量子算法還很少.再者還有更多貼近實際應用的優化問題，如引入更多約束條件的約束優化、目標函數不單一的多目標規劃、帶有不確定性的不確定規劃、問題隨時間而變的動態規劃、部分變量要求為整數的混合整數規劃等.經典優化對于這些優化問題均有系統的研究，而量子計算目前依然缺席，均可進行探索.