基于帝國(guó)競(jìng)爭(zhēng)優(yōu)化的雙目標(biāo)綜合決策選星算法

邱明 嚴(yán)勇杰 孫蕊 張文宇

(1. 南京航空航天大學(xué) 民航學(xué)院, 南京 211106; 2. 空中交通管理系統(tǒng)與技術(shù)國(guó)家重點(diǎn)實(shí)驗(yàn)室, 南京 210007)

隨著全球衛(wèi)星導(dǎo)航系統(tǒng)(GNSS)的快速發(fā)展,其被廣泛運(yùn)用在工程應(yīng)用中(測(cè)量、導(dǎo)航等)為人類(lèi)帶來(lái)了巨大的社會(huì)和經(jīng)濟(jì)效益[1]。 然而,快速發(fā)展的同時(shí)對(duì)目前的全球衛(wèi)星導(dǎo)航系統(tǒng)的導(dǎo)航性能提出了更高的要求,其中包括更好的實(shí)時(shí)性、更高的精度和更強(qiáng)的可靠性。 在此背景下,各國(guó)大力發(fā)展自己的全球衛(wèi)星導(dǎo)航系統(tǒng),其中包括中國(guó)的BDS、美國(guó)的GPS、俄羅斯的GLONASS 以及歐盟的Galileo。 全球衛(wèi)星導(dǎo)航系統(tǒng)隨著多星座建設(shè)的發(fā)展,未來(lái)四大全球衛(wèi)星導(dǎo)航系統(tǒng)將提供超過(guò)百顆的衛(wèi)星供用戶(hù)接收機(jī)進(jìn)行導(dǎo)航服務(wù)[2]。 雖然,這將極大提高用戶(hù)的可用衛(wèi)星數(shù),然而過(guò)多的可見(jiàn)衛(wèi)星提供的冗余信息也會(huì)增加接收機(jī)導(dǎo)航定位解算的耗時(shí)。 在滿(mǎn)足實(shí)際應(yīng)用過(guò)程中定位結(jié)果的精度要求下,為了提高接收機(jī)實(shí)時(shí)解算的性能,可以從接收機(jī)觀測(cè)到的所有可見(jiàn)衛(wèi)星中挑選出幾何布局較好的星座進(jìn)行定位解算[3],這種選取衛(wèi)星的方法稱(chēng)之為選星。 目前的選星算法從單衛(wèi)星導(dǎo)航系統(tǒng)選星發(fā)展而來(lái),一般通過(guò)最小幾何精度因子(Geometric Dilution Precision, GDOP)方法、遍歷法或者最大體積法選取固定數(shù)目衛(wèi)星中幾何構(gòu)型最好星座進(jìn)行解算[4-5],但計(jì)算量巨大,無(wú)法保 證 實(shí) 時(shí) 性。 Mosavi 和 Divband[6]認(rèn) 為 最 小GDOP 方法在實(shí)踐中仍然是首選的衛(wèi)星選擇方法,剩下的問(wèn)題是簡(jiǎn)化GDOP 的計(jì)算,為了提高計(jì)算效率,其提出了基于進(jìn)化算法(EA)的自適應(yīng)濾波技術(shù)來(lái)計(jì)算GDOP 的方法,結(jié)果顯示,可用自適應(yīng)濾波技術(shù)的算法近似計(jì)算GDOP,但還是存在著一定的誤差[6]。 為了提高準(zhǔn)確性,后續(xù)的研究人員提出了其他的改進(jìn)算法。 王爾申等[7]基于粒子群優(yōu)化(Particle Swarm Optimization, PSO)算法固定選星數(shù)目,依據(jù)最小GDOP 值進(jìn)行選星,降低了選星耗時(shí),提高了選星的有效性。 霍航宇和張曉林[8]將多系統(tǒng)選星算法視作單目標(biāo)優(yōu)化,根據(jù)用戶(hù)所需精度固定不同的衛(wèi)星數(shù)目進(jìn)行定位解算。 Azami 和Sanei[9]運(yùn)用神經(jīng)網(wǎng)絡(luò)算法對(duì)星座的GDOP 進(jìn)行分類(lèi),更快地獲取GDOP小的衛(wèi)星星座。 宋丹等[10]也將遺傳算法用到選星中,結(jié)果表明, 遺傳算法比遍歷法耗時(shí)短。Wu 等[11]基于支持向量機(jī)算法逼近星座的GDOP,避免計(jì)算時(shí)復(fù)雜的矩陣求逆轉(zhuǎn)置等步驟。 劉季等[12]也從高度角出發(fā)以及考慮GDOP值進(jìn)行組合選星。 但上述幾種選星算法都是先固定選星數(shù)目,再在所有的固定衛(wèi)星數(shù)目星座中選出最小GDOP 的衛(wèi)星星座。 可是實(shí)際運(yùn)用于接收機(jī)時(shí),接收機(jī)觀測(cè)衛(wèi)星數(shù)會(huì)隨著時(shí)間發(fā)生變換,同時(shí)隨著四大全球衛(wèi)星導(dǎo)航系統(tǒng)的發(fā)展,用戶(hù)接收機(jī)觀測(cè)到的可見(jiàn)衛(wèi)星將多達(dá)幾十顆,此時(shí)提前固定選星顆數(shù)值得商榷。 因此,當(dāng)前的選星算法存在著不能靈活的固定選星數(shù)目的問(wèn)題,具有很大的局限性。 有必要同時(shí)考慮衛(wèi)星數(shù)目和定位結(jié)果的精度,從這2 個(gè)目標(biāo)出發(fā)進(jìn)行選星。

近年來(lái)有學(xué)者從多目標(biāo)優(yōu)化出發(fā),如徐小鈞等[13-14]基于NSGA-II 遺傳算法將GDOP 值和選星數(shù)目視作2 個(gè)目標(biāo)進(jìn)行多目標(biāo)快速選星,仿真表明其在靜態(tài)和動(dòng)態(tài)情況下有良好的表現(xiàn)。 雖然運(yùn)用遺傳算法進(jìn)行多目標(biāo)優(yōu)化是一個(gè)可行的方法,然而過(guò)程比較繁瑣,同時(shí)選星時(shí)未考慮引入衛(wèi)星仰角和方向角等先驗(yàn)信息。 針對(duì)上述選星算法存在的問(wèn)題,本文采取了基于帝國(guó)競(jìng)爭(zhēng)優(yōu)化算法(ICA)的雙目標(biāo)綜合決策選星算法。 充分利用帝國(guó)競(jìng)爭(zhēng)優(yōu)化算法的復(fù)雜度低、計(jì)算量少的優(yōu)點(diǎn)以及利用所選星座的GDOP(能夠間接反映出定位結(jié)果的精度)和選星數(shù)目2 個(gè)目標(biāo)進(jìn)行綜合決策;為了更好地獲取幾何構(gòu)型好的衛(wèi)星星座,本文通過(guò)引入可見(jiàn)衛(wèi)星的衛(wèi)星仰角和方向角先驗(yàn)信息,進(jìn)行先驗(yàn)性約束,有效解決了呆板的固定選星數(shù)目的問(wèn)題。 同時(shí)在雙目標(biāo)綜合決策時(shí),不采用復(fù)雜度高的多目標(biāo)優(yōu)化算法,而是依據(jù)2 個(gè)目標(biāo)的相關(guān)性,將2 個(gè)目標(biāo)結(jié)合成1 個(gè)聯(lián)合目標(biāo)進(jìn)行綜合決策,極大降低了算法的復(fù)雜性,從而縮短了計(jì)算時(shí)間。 因此,衛(wèi)星接收機(jī)不僅不需要提前固定選星數(shù)目,還能提高接收機(jī)的計(jì)算效率,同時(shí)引入先驗(yàn)性約束后的選星結(jié)果的GDOP 值滿(mǎn)足用戶(hù)精度要求,較無(wú)約束下的選星后的GDOP 值有所減小,對(duì)定位有重要意義。

1 多星座GDOP

在全球衛(wèi)星導(dǎo)航系統(tǒng)中,用戶(hù)通過(guò)接收機(jī)獲得的自身定位結(jié)果精度與接收機(jī)中觀測(cè)到的可見(jiàn)衛(wèi)星組成的衛(wèi)星星座的幾何構(gòu)型以及測(cè)量的偽距值的誤差有關(guān),其中衛(wèi)星星座的幾何構(gòu)型可以用GDOP 來(lái)反映[13]。

式中:下標(biāo)GPS、GLO、GAL、BDS 分別代表GPS、GLONASS、Galileo 和BDS 系統(tǒng)[13];H為一個(gè)n×7維的觀測(cè)矩陣,n為接收機(jī)觀測(cè)到的全部衛(wèi)星導(dǎo)航系統(tǒng)下的總可見(jiàn)衛(wèi)星顆數(shù);HGPS為GPS 系統(tǒng)下的觀測(cè)矩陣的前3 列;HGLO、HGAL、HBDS分別為GLONASS、Galileo、BDS 衛(wèi) 星 導(dǎo) 航 系 統(tǒng) 下 觀 測(cè) 矩陣的前3 列;H的后4 列中,1x和0x分別為x衛(wèi)星導(dǎo)航系統(tǒng)下對(duì)應(yīng)可見(jiàn)衛(wèi)星數(shù)目維全為1 和0的列向量[13]。 同時(shí),為了進(jìn)一步從接收機(jī)的角度講述多星座選星的意義,本文從衛(wèi)星可見(jiàn)數(shù)目出發(fā),分析選星數(shù)目與GDOP 的關(guān)系,選取GPS +GLO + BDS 三系統(tǒng)下一個(gè)歷元采集到的數(shù)據(jù),其觀測(cè)到的可見(jiàn)衛(wèi)星總數(shù)為25,確定不同選星數(shù)目(在三系統(tǒng)下,有6 個(gè)未知數(shù),因此選星數(shù)目從6 出發(fā)),采用最小GDOP 方法,將不同選星數(shù)目下選星后的最小GDOP 值與全部可見(jiàn)衛(wèi)星下計(jì)算得到的最小GDOP 值記錄,其結(jié)果如表1 所示。

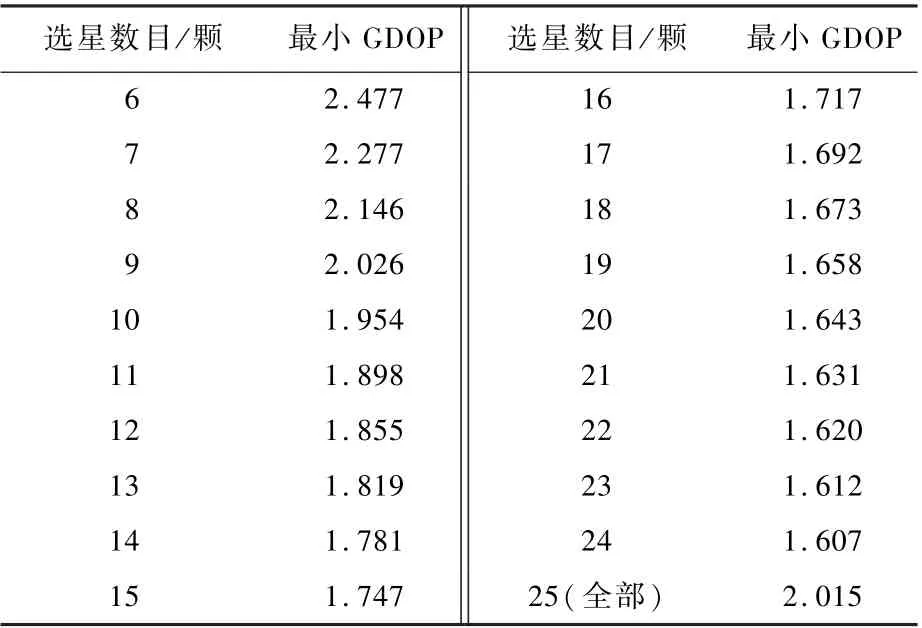
表1 GPS +GLONASS +BDS 下不同選星數(shù)目后的最小GDOPTable 1 Minimum GDOP with different numbers of selected satellites (GPS +GLONASS +BDS)

2 基于帝國(guó)競(jìng)爭(zhēng)優(yōu)化的選星算法

可知,隨著選星數(shù)目的增加,GDOP 值非線性遞減, 同時(shí)GDOP 下降越慢,選星數(shù)目超過(guò)9 后的GDOP 比全部可見(jiàn)衛(wèi)星下的GDOP 還小,這說(shuō)明全部可見(jiàn)衛(wèi)星中存在某些衛(wèi)星使全部可見(jiàn)衛(wèi)星下的幾何構(gòu)型變差,導(dǎo)致GDOP 值變大。 從而選星可能不僅能夠降低可見(jiàn)衛(wèi)星數(shù)目,減少接收機(jī)的功耗,也可能在選星過(guò)程中,刪除一些幾何構(gòu)型差的衛(wèi)星。 因此,本文為了使選星后的衛(wèi)星星座的幾何構(gòu)型盡可能較好,依據(jù)可見(jiàn)衛(wèi)星的方向角和衛(wèi)星仰角先驗(yàn)信息,引入先驗(yàn)性約束,將所有的可見(jiàn)衛(wèi)星按照方向角0° ～90°,90° ～180°,180° ～270°,270° ～360° 4 個(gè)區(qū)間,劃分到對(duì)應(yīng)不同區(qū)間,再?gòu)拿總€(gè)區(qū)間中選取該區(qū)間下衛(wèi)星高度角最大的衛(wèi)星,從而使衛(wèi)星分布較廣,如圖1所示,菱形點(diǎn)為引入先驗(yàn)性約束后選取的初始4 顆衛(wèi)星。

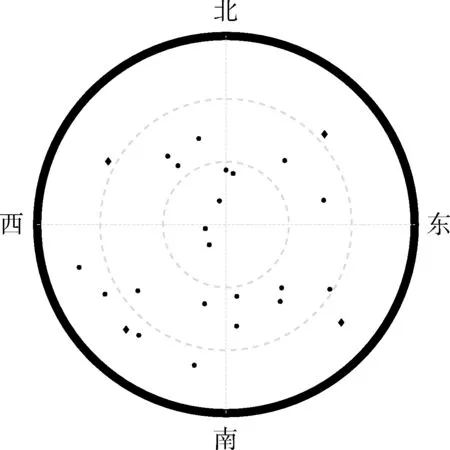
圖1 先驗(yàn)性約束下選取的初始衛(wèi)星Fig.1 Initial satellites selected with a priori constraint

針對(duì)從多個(gè)衛(wèi)星導(dǎo)航系統(tǒng)的可見(jiàn)衛(wèi)星中快速選出幾何結(jié)構(gòu)較好的星座,本文提出一種基于帝國(guó)競(jìng)爭(zhēng)優(yōu)化的雙目標(biāo)綜合決策選星算法。 帝國(guó)競(jìng)爭(zhēng)優(yōu)化算法是一種通過(guò)模擬帝國(guó)主義殖民競(jìng)爭(zhēng)機(jī)制進(jìn)行隨機(jī)優(yōu)化搜索的算法[15]。 基于帝國(guó)競(jìng)爭(zhēng)優(yōu)化算法,本文首先根據(jù)衛(wèi)星接收機(jī)接收到的衛(wèi)星數(shù)據(jù)中觀測(cè)到的衛(wèi)星總數(shù)進(jìn)行編碼,引入可見(jiàn)衛(wèi)星的衛(wèi)星仰角和方向角先驗(yàn)信息,初始化原始國(guó)家時(shí)依據(jù)衛(wèi)星仰角和方向角進(jìn)行先驗(yàn)性約束;然后計(jì)算原始國(guó)家的GDOP 和選星數(shù)目雙目標(biāo)聯(lián)合決策成本值來(lái)劃分初始帝國(guó),根據(jù)劃分的對(duì)應(yīng)帝國(guó)來(lái)同化帝國(guó)對(duì)應(yīng)分配的殖民地,同化后進(jìn)行國(guó)家改革,所有國(guó)家改革后,進(jìn)行帝國(guó)更換,更換后的不同帝國(guó)相互競(jìng)爭(zhēng),強(qiáng)大帝國(guó)奪取弱小帝國(guó)殖民地,弱小帝國(guó)無(wú)殖民地后滅亡,淪為強(qiáng)大帝國(guó)殖民地;最后收斂出最優(yōu)結(jié)果,進(jìn)行譯碼,得出所選衛(wèi)星號(hào)。 圖2 為詳細(xì)的算法流程。

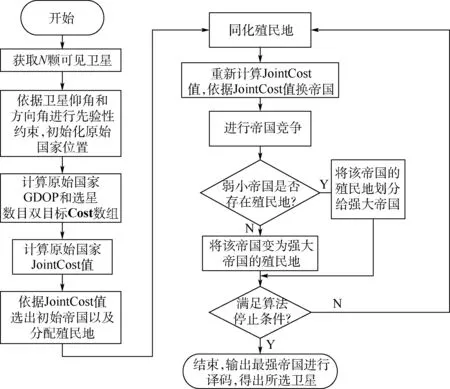
圖2 基于帝國(guó)競(jìng)爭(zhēng)優(yōu)化的選星算法流程Fig.2 Process of ICA satellite selection algorithm

該算法的主要步驟如下:

步驟1 將所有符合條件的可見(jiàn)的衛(wèi)星提取出,得到其總數(shù)N。

步驟2 初始化系統(tǒng)參數(shù)和帝國(guó)。 其中初始化帝國(guó)包括初始化殖民地以及原始帝國(guó)2 個(gè)部分。 首先根據(jù)可見(jiàn)衛(wèi)星總數(shù)N,將所有衛(wèi)星編號(hào)為1 ～N,將所有的可見(jiàn)衛(wèi)星按照方向角0° ～90°,90° ～180°,180° ～270°,270° ～360° 4 個(gè)區(qū)間,劃分到對(duì)應(yīng)不同區(qū)間,從每個(gè)區(qū)間中選取該區(qū)間下衛(wèi)星高度角最大的衛(wèi)星,對(duì)應(yīng)衛(wèi)星編號(hào)位置編碼為1,根據(jù)設(shè)定的國(guó)家數(shù)nPop,隨機(jī)選取nPop 種組合為原始國(guó)家,即在其他衛(wèi)星編號(hào)位置處將選取到的衛(wèi)星在對(duì)應(yīng)衛(wèi)星號(hào)編碼為1,沒(méi)有選取到的衛(wèi)星對(duì)應(yīng)編碼為0。 將該原始國(guó)家的連續(xù)N個(gè)編碼作為原始國(guó)家的位置,建立一個(gè)N維變量的數(shù)組來(lái)表示原始國(guó)家的位置,即X。

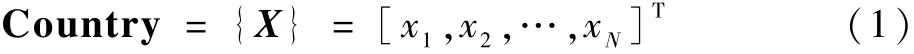
計(jì)算每個(gè)原始國(guó)家的成本(Cost)值:

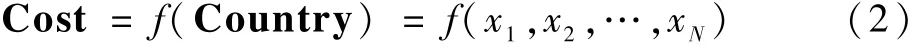
式中:f(·)為計(jì)算成本Cost 值的函數(shù)。 本文中Cost 值指的是每種組合的GDOP 值和選取的選星數(shù)目的二維數(shù)組。 得到所有原始國(guó)家的成本值后,計(jì)算一個(gè)雙目標(biāo)聯(lián)合決策成本值JointCost,這是因?yàn)楸疚乃惴ㄓ?jì)算的成本值是二維數(shù)組,無(wú)法直接比較,但是通過(guò)表1 結(jié)果分析可知,當(dāng)衛(wèi)星數(shù)目增多時(shí),其對(duì)應(yīng)的GDOP 值下降,可知選星數(shù)目與GDOP 值存在相關(guān)關(guān)系。 因此,可以將二者聯(lián)系起來(lái),形成一個(gè)雙目標(biāo)聯(lián)合決策成本值Joint-Cost。 為了計(jì)算出該聯(lián)合成本值,設(shè)計(jì)了一個(gè)對(duì)應(yīng)計(jì)算函數(shù),具體公式如下:

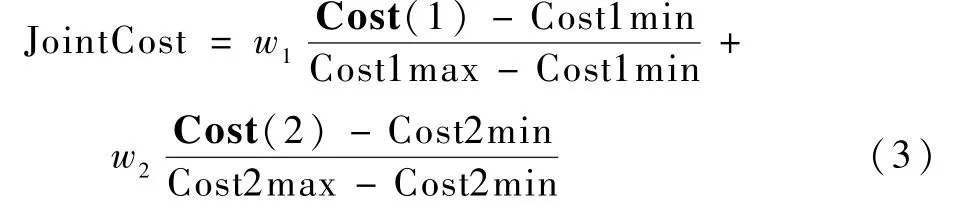
式中:w1和w2為對(duì)應(yīng)的權(quán)重,取決于用戶(hù)的偏好,也能更好反映出當(dāng)考慮衛(wèi)星數(shù)和GDOP 兩個(gè)成本值時(shí),算法可以人為地選擇偏重哪一方,從而使接收機(jī)更有靈活性;Cost(1)和Cost(2)分別為原始國(guó)家成本值二維數(shù)組中的選星數(shù)目和GDOP值;Cost1max 和Cost1min 分別為所有原始國(guó)家成本中選星數(shù)目的最大值和最小值;Cost2max 和Cost2min 分別為所有原始國(guó)家成本中GDOP 最大值和最小值。 計(jì)算完所有原始國(guó)家的聯(lián)合成本值后,將初始化帝國(guó)。 選取帝國(guó)的原則是依據(jù)每個(gè)國(guó)家的權(quán)力值選取權(quán)力值大的前幾個(gè)國(guó)家為帝國(guó)。而國(guó)家的權(quán)力值與國(guó)家的聯(lián)合成本值成反比,即聯(lián)合成本值小的國(guó)家,權(quán)力則大。 因此,本文將聯(lián)合成本值低的前幾個(gè)國(guó)家選取為帝國(guó),然后依據(jù)每個(gè)帝國(guó)的權(quán)力值將未成為帝國(guó)的國(guó)家視作殖民地,對(duì)其進(jìn)行劃分[16]。 分配殖民地時(shí),首先標(biāo)準(zhǔn)化每個(gè)帝國(guó)的聯(lián)合成本,確定每個(gè)帝國(guó)的權(quán)力值。

式中:cM為第M個(gè)帝國(guó)的聯(lián)合成本值;CM為第M個(gè)帝國(guó)的標(biāo)準(zhǔn)化聯(lián)合成本值; max{ci} 為全部帝國(guó)中最大聯(lián)合成本值。 有了所有帝國(guó)的標(biāo)準(zhǔn)化聯(lián)合成本值后,定義每個(gè)帝國(guó)的權(quán)力為

式中:MCM為第M個(gè)帝國(guó)的殖民地的數(shù)量;Mcol為殖民地總數(shù),即未能成為帝國(guó)的原始國(guó)家總數(shù);round 為取整函數(shù),即將PM·Mcol的結(jié)果按照四舍五入取整。

步驟3 同化殖民地。 帝國(guó)為了鞏固在殖民地中的主體地位,迫使殖民地學(xué)習(xí)自己的文化,這種控制殖民地的方式稱(chēng)為同化。 在帝國(guó)競(jìng)爭(zhēng)優(yōu)化算法中,將同化的方式模擬為讓殖民地的位置向帝國(guó)的位置靠近。 其中每個(gè)殖民地向帝國(guó)靠近的距離為y～U(0,β×d),即y是一個(gè)在β×d內(nèi)均勻分布的隨機(jī)數(shù)[16],d為殖民地與帝國(guó)之間的距離,β一般取值大于1。 具體同化的公式如下:

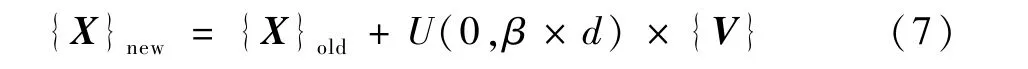
式中:{V} 為殖民地靠近帝國(guó)時(shí)的移動(dòng)方向;{X}old為殖民地原先位置;{X}new為殖民地同化后的位置。 同化殖民地后,重新計(jì)算帝國(guó)和帝國(guó)下的殖民地對(duì)應(yīng)的雙目標(biāo)聯(lián)合決策成本值,如果殖民地中新計(jì)算的聯(lián)合成本值小于帝國(guó)的聯(lián)合成本值,則將該殖民地替換為新的帝國(guó),也稱(chēng)為換帝。

步驟4 國(guó)家改革。 由于最開(kāi)始的帝國(guó)競(jìng)爭(zhēng)優(yōu)化算法會(huì)陷入局部最優(yōu)解,后續(xù)研究者加入了國(guó)家改革這一環(huán)節(jié)。 事先設(shè)定國(guó)家發(fā)生改革的概率,如果該國(guó)家發(fā)生了改革,則將改革后的成本值與改革前進(jìn)行比較。 由于本文國(guó)家的成本值為GDOP和選星數(shù)目雙目標(biāo)二維數(shù)組,無(wú)法直接比較,按照雙目標(biāo)聯(lián)合決策成本值計(jì)算公式,計(jì)算對(duì)應(yīng)的值,取小者對(duì)應(yīng)的位置為該國(guó)家新的位置。 這樣就能使帝國(guó)和殖民地在一定概率下都能進(jìn)行位置的自我更新,緩解了算法陷入局部最優(yōu)解的難題。

步驟5 帝國(guó)競(jìng)爭(zhēng)。 為了更好體現(xiàn)不同帝國(guó)競(jìng)爭(zhēng)時(shí)帝國(guó)之間的權(quán)力值,帝國(guó)競(jìng)爭(zhēng)時(shí)將考慮帝國(guó)的成本值以及所擁有的殖民地的成本值,即總成本值。 因此,首先計(jì)算帝國(guó)的總成本值。 然后根據(jù)帝國(guó)的總成本值確定其權(quán)力值,其總成本值計(jì)算公式為

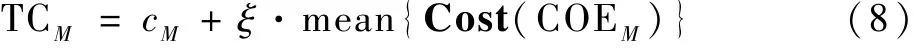
式中:TCM為第M個(gè)帝國(guó)的總成本值;0 <ξ<1;mean{Cost(COEM)}為該帝國(guó)所有殖民地的聯(lián)合成本值JointCost 的平均值。 由于本文成本值為雙目標(biāo)二維數(shù)組,將總成本計(jì)算公式中的成本值cM替換為對(duì)應(yīng)帝國(guó)及其殖民地的雙目標(biāo)聯(lián)合決策成本值JointCost。

最后和初始化帝國(guó)時(shí)標(biāo)準(zhǔn)化帝國(guó)的聯(lián)合成本值一樣,標(biāo)準(zhǔn)化所有帝國(guó)的總聯(lián)合決策成本值,得到每個(gè)帝國(guó)的標(biāo)準(zhǔn)化總聯(lián)合決策成本值MTCM。

D中最大值對(duì)應(yīng)權(quán)力最強(qiáng)大帝國(guó), 然后權(quán)力最強(qiáng)大帝國(guó)掠奪D中最小值對(duì)應(yīng)帝國(guó)的殖民地。

步驟6 帝國(guó)滅亡。 如果最弱帝國(guó)沒(méi)有殖民地了,則劃分為權(quán)力最大的帝國(guó)的殖民地。 判斷是否迭代完畢,如果沒(méi)有,則返回步驟3,迭代完畢則輸出最后結(jié)果。

步驟7 輸出最后結(jié)果。 即雙目標(biāo)聯(lián)合決策成本值最小的帝國(guó),然后將得到的結(jié)果進(jìn)行譯碼,即該帝國(guó)位置中編碼為1 的衛(wèi)星號(hào),為所需要選取的衛(wèi)星。 同時(shí)提取出對(duì)應(yīng)的成本值,即對(duì)應(yīng)的衛(wèi)星數(shù)目以及GDOP 值。 通過(guò)其GDOP 值以及選星數(shù)目,可以驗(yàn)證算法的有效性。

3 實(shí)驗(yàn)仿真與實(shí)測(cè)數(shù)據(jù)

3.1 GPS +GLONASS +BDS 仿真

為了驗(yàn)證本文算法的實(shí)時(shí)性以及有效性,仿真了3 個(gè)全球衛(wèi)星導(dǎo)航系統(tǒng)下衛(wèi)星數(shù)據(jù),3 個(gè)全球?qū)Ш较到y(tǒng)分別為GPS、GLONASS、BDS。 在3 個(gè)全球衛(wèi)星導(dǎo)航系統(tǒng)組合導(dǎo)航的情況下,進(jìn)行了仿真,仿真時(shí)間為24 h,仿真地點(diǎn)為南京,地理坐標(biāo)為北緯32°02′38″、東經(jīng)118°46′43″。 通過(guò)本文算法的單次選星耗時(shí)來(lái)反映實(shí)時(shí)性,以及通過(guò)算法引入先驗(yàn)性約束和無(wú)先驗(yàn)性約束下最后選星結(jié)果中的GDOP 與實(shí)測(cè)數(shù)據(jù)中總可見(jiàn)衛(wèi)星數(shù)目的GDOP 進(jìn)行對(duì)比和選星數(shù)目是否降低2 個(gè)方面來(lái)反映算法的有效性,同時(shí)由于在實(shí)際接收機(jī)進(jìn)行解算的時(shí)候,會(huì)篩選出高度角小的衛(wèi)星,使定位結(jié)果更加準(zhǔn)確。 因此,為了進(jìn)一步驗(yàn)證本文算法,選取仿真中高度截止角5°和10°下的實(shí)驗(yàn)數(shù)據(jù)進(jìn)行驗(yàn)證。

3.1.1 有效性分析

高度截止角5°和10°仿真條件下的選星前后對(duì)比如圖3 和圖4 所示,表2 為統(tǒng)計(jì)分析,表3 為縮減衛(wèi)星時(shí),本文算法無(wú)先驗(yàn)性約束和先驗(yàn)性約束下的平均選星數(shù)目比較。

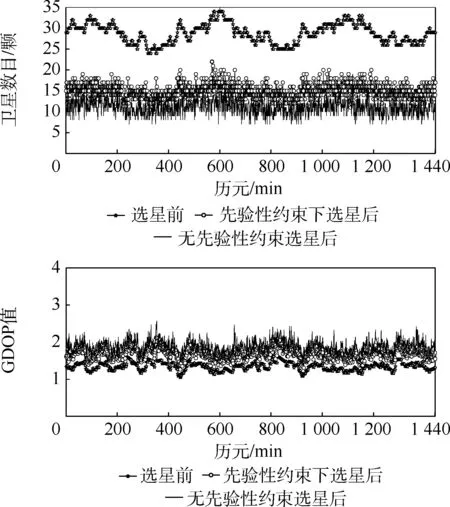
圖3 截止高度角5°下的選星前后對(duì)比Fig.3 Comparisons before and after satellite selection with an elevation angle of 5°

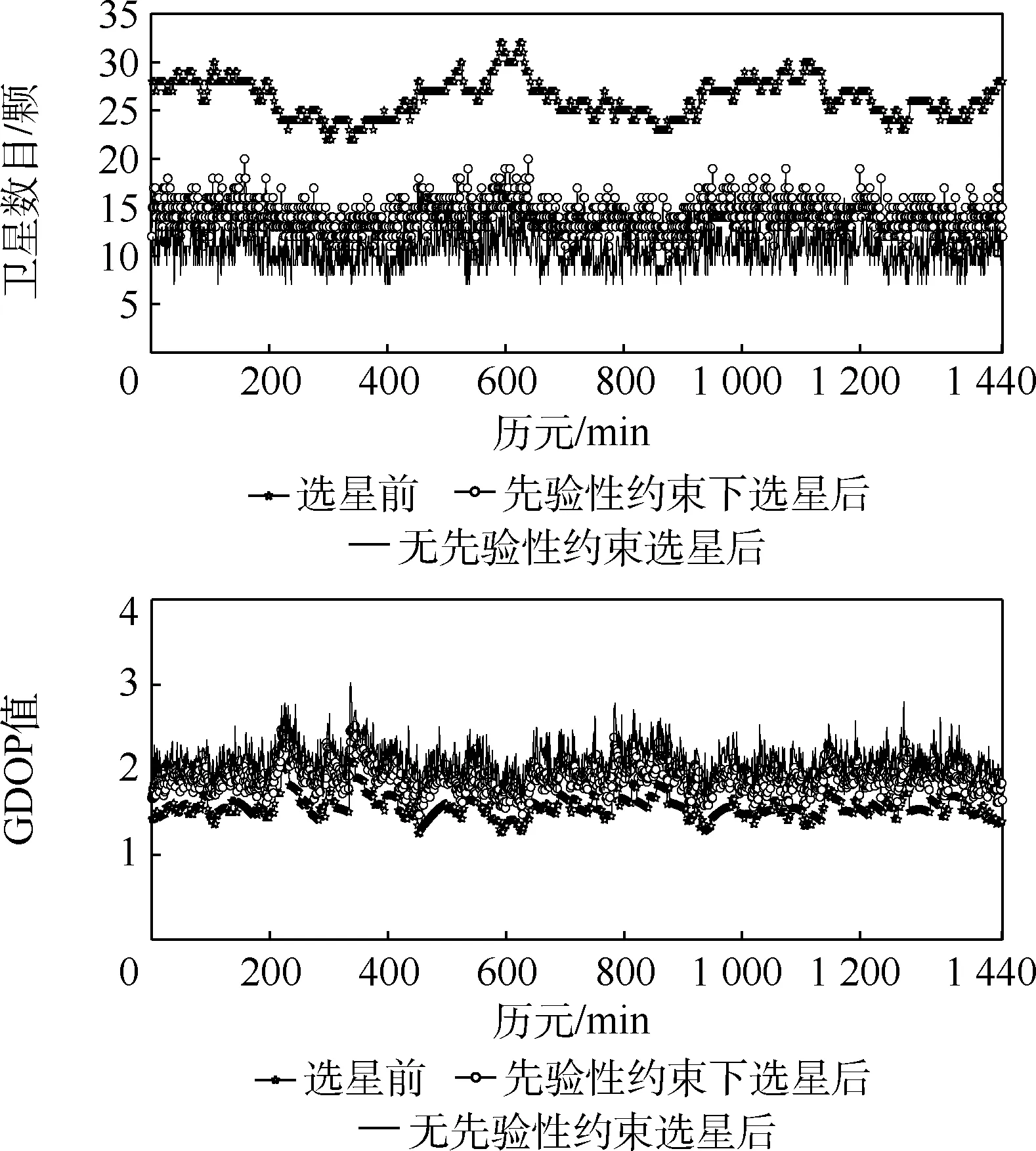
圖4 截止高度角10°下的選星前后對(duì)比Fig.4 Comparisons before and after satellite selection with an elevation angle of 10°

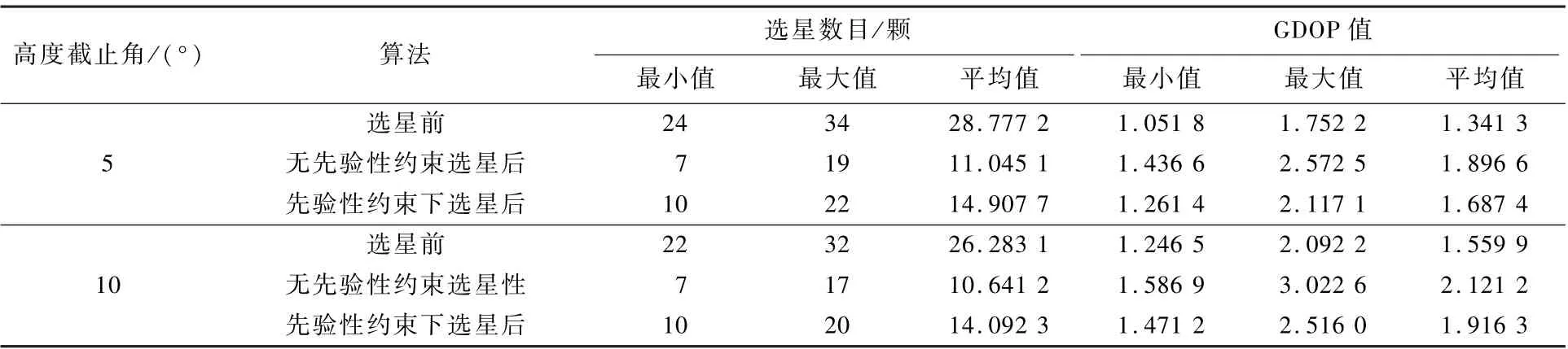
表2 GPS +GLONASS +BDS 下選星前后對(duì)比分析Table 2 Comparative analysis before and after satellite selection (GPS +GLONASS +BDS)

表3 有/無(wú)先驗(yàn)性約束下平均選星數(shù)目對(duì)比Table 3 Comparison of average satellite selection number with /without a priori constraint

從圖3、圖4 的關(guān)系曲線以及表2、表3 的統(tǒng)計(jì)分析中,可得出以下結(jié)論:

1) 當(dāng)高度截止角選取為5°和10°時(shí),本文算法無(wú)論有無(wú)先驗(yàn)性約束選星數(shù)目總體變化趨勢(shì)都與仿真下的總可見(jiàn)衛(wèi)星顆數(shù)相似,同時(shí)對(duì)應(yīng)的GDOP 變化趨勢(shì)同樣與其總可見(jiàn)衛(wèi)星顆數(shù)對(duì)應(yīng)星座的GDOP 變化趨勢(shì)相似,說(shuō)明本文算法具有穩(wěn)定性。

2) 高度截止角為5°時(shí),無(wú)先驗(yàn)性約束下選星后的選星數(shù)目的平均值為選星前的38.4%,當(dāng)高度角選取為10°,選星后的選星數(shù)目的平均值為選星前的39.9%,當(dāng)引入先驗(yàn)性約束后,選星后的選星數(shù)目在高度截止角為5°和10°下,分別為51.8%和48.97%。 說(shuō)明無(wú)論是否存在約束本文算法都能夠充分降低選星數(shù)目。 同時(shí)如表3 所示,高度截止角為5°下引入先驗(yàn)性約束后縮減率51.8%較無(wú)先驗(yàn)性約束下的縮減率38. 4% 增加了13.4%,說(shuō)明引入先驗(yàn)性約束后選星數(shù)目增加了,但是相對(duì)于選星前的總可見(jiàn)衛(wèi)星數(shù)依舊減少了48.2%,有效降低了衛(wèi)星數(shù)目。

3) 當(dāng)引入先驗(yàn)性約束后,在高度截止角5°和10°下,選星后的GDOP 平均值1.687 4 和1.916 3相對(duì)于無(wú)先驗(yàn)性約束選星后的1.896 6 和2.121 2降低了0.209 2 和0.204 9,說(shuō)明引入先驗(yàn)性約束后,本文算法更能有效地選取幾何構(gòu)型好的衛(wèi)星星座。 同時(shí),當(dāng)GDOP 值小于6 時(shí),滿(mǎn)足全球衛(wèi)星導(dǎo)航系統(tǒng)的有效性要求,但為了用戶(hù)擁有更好的精度,通常需要將GDOP 值控制在4 以?xún)?nèi)的范圍[17]。 本文算法無(wú)論是否引入先驗(yàn)性約束,選星后都將GDOP 控制在小于4 的范圍內(nèi),說(shuō)明本文算法能夠滿(mǎn)足用戶(hù)精度要求。 同時(shí),為了進(jìn)一步描述引入先驗(yàn)性約束后選星前后的GDOP 變化,本文對(duì)整個(gè)仿真過(guò)程中引入先驗(yàn)性約束后的選星后的GDOP 與選星前(總可見(jiàn)衛(wèi)星數(shù)的GDOP)的差值進(jìn)行分析,其中高度截止角5°和10°下的選星前后GDOP 差值的統(tǒng)計(jì)分析如表4 所示。 前后GDOP 差值的方差用來(lái)表示差值的穩(wěn)定程度,從而反映選星算法的穩(wěn)定性。

表4 選星前和先驗(yàn)性約束下選星后GDOP 差值在各區(qū)間下的百分比Table 4 Percentage of GDOP difference before and after satellite selection with a priori constraint in each interval

如表4 所示,本文將每次引入先驗(yàn)性約束后的選星前后GDOP 差值劃為[0,0.1),[0. 1,0. 2),[0.2,0.3),[0.3,0.4),[0.4,0.5]5 個(gè)區(qū)間,由表4 可知,選星前后GDOP 差值主要分布在[0.3,0.4)區(qū)間,與選星后的GDOP 平均值相對(duì)于選星前的GDOP 平均值增加量小于0.4 一致。同時(shí)選星前后GDOP 值的差值的方差較小,說(shuō)明選星前后GDOP 差值比較穩(wěn)定,保持了良好的有效性。

3.1.2 實(shí)時(shí)性分析

在高度截止角5°仿真條件下引入先驗(yàn)性約束和無(wú)約束下的單次選星耗時(shí)對(duì)比如圖5 所示,表5 為統(tǒng)計(jì)分析,表6 為有無(wú)/先驗(yàn)性約束下單次選星平均耗時(shí)與遍歷法對(duì)比。

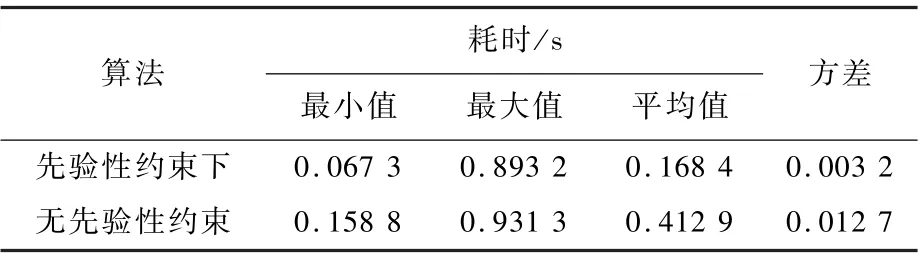
表5 截止高度角5°下有/無(wú)先驗(yàn)性約束單次選星耗時(shí)數(shù)據(jù)統(tǒng)計(jì)Table 5 Statistics of time consumption for one-time satellite selection with/without prior constraint at an elevation angle of 5°

表6 單次選星平均耗時(shí)算法性能比較Table 6 Comparison of time consumption of one-time satellite selection by candidate algorithms

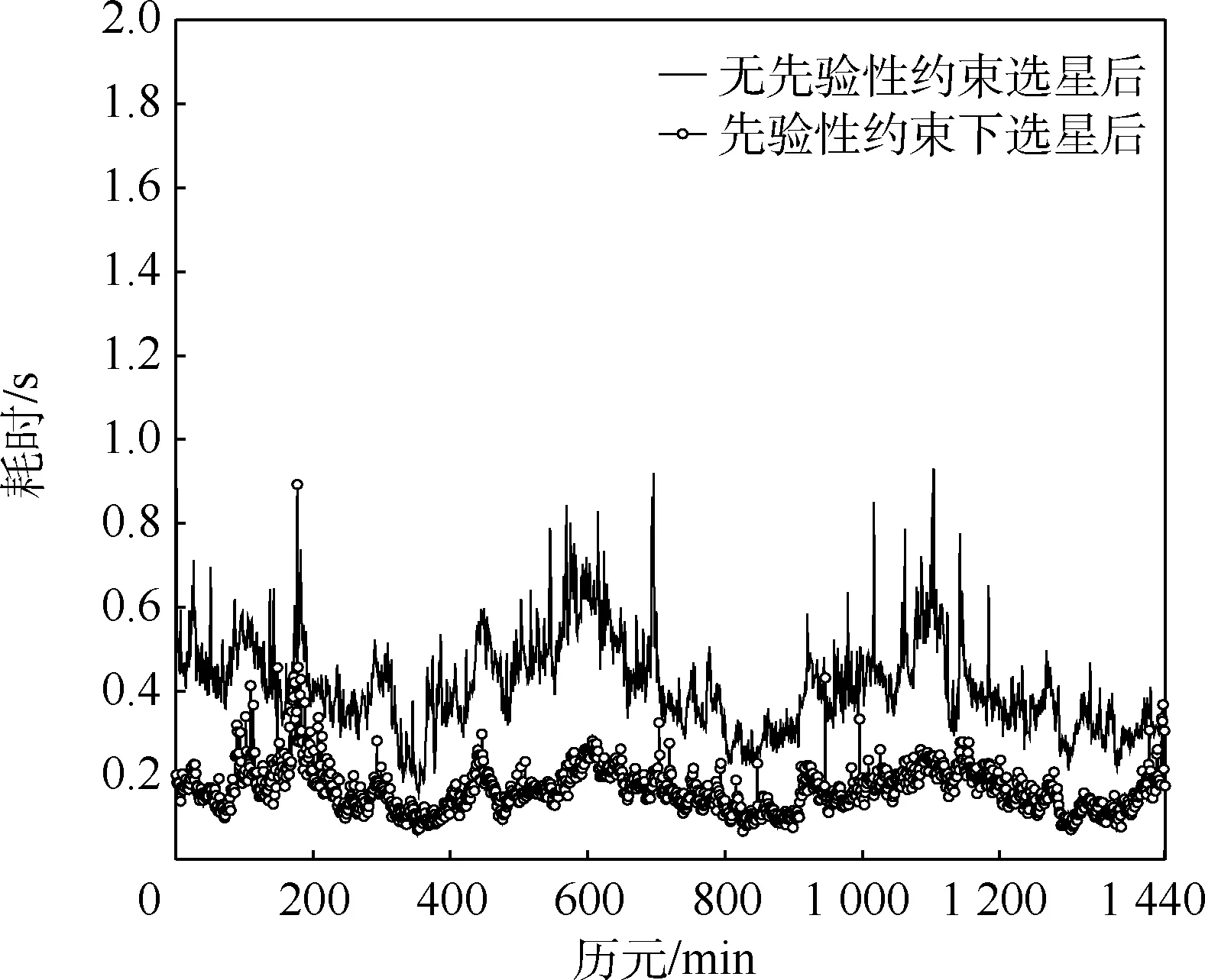
圖5 截止高度角5°下有/無(wú)先驗(yàn)性約束單次選星耗時(shí)Fig.5 Time consumption of one-time satellite selection with/without prior constraint at an elevation angle of 5°

從圖5 的關(guān)系曲線以及表5、表6 的統(tǒng)計(jì)分析中,可得出以下結(jié)論:

1) 在高度截止角選取為5°時(shí),本文算法在無(wú)約束條件下單次選星所用最長(zhǎng)時(shí)間為0.931 3 s,引入先驗(yàn)性約束后,單次選星所用最長(zhǎng)時(shí)間為0.893 2 s,兩者都比遍歷法的4 s 所用時(shí)間少,分別提高76.72%和77.67%,實(shí)時(shí)性強(qiáng)。

2) 在高度截止角選取為5°下,本文算法在無(wú)約束條件下和約束下單次選星所用平均時(shí)間分別為0.412 9 s 和0.168 4 s,說(shuō)明引入先驗(yàn)性約束后,算法耗時(shí)降低,兩者相對(duì)于遍歷法4 s,分別提高了89.68%和95.79%,進(jìn)一步說(shuō)明本文算法的實(shí)時(shí)性。

3) 無(wú)論是在無(wú)約束條件下還是引入先驗(yàn)性約束后,選星所用時(shí)間的方差都較小,說(shuō)明本文算法選星耗時(shí)方面穩(wěn)定性強(qiáng),具有良好的實(shí)時(shí)性的同時(shí)依舊保持著有效性。

3.2 GPS +GLONASS +BDS 實(shí)測(cè)數(shù)據(jù)

為了驗(yàn)證本文算法在實(shí)際運(yùn)用中的有效性以及實(shí)時(shí)性,本文在南京航空航天大學(xué)收集了GPS +GLONASS + BDS 系統(tǒng)的實(shí)測(cè)數(shù)據(jù),對(duì)選星情況進(jìn)行了實(shí)測(cè)數(shù)據(jù)驗(yàn)證,時(shí)長(zhǎng)為2 h,實(shí)驗(yàn)地點(diǎn)為地理坐標(biāo)(北緯31°56′20″、東經(jīng)118°47′04″),高度截止角選取為5°,采集數(shù)據(jù)環(huán)境如圖6所示。

圖6 采集數(shù)據(jù)環(huán)境Fig.6 Environment of data collection

3.2.1 有效性分析

實(shí)測(cè)數(shù)據(jù)高度截止角5°下的選星前后對(duì)比如圖7 所示,表7 為統(tǒng)計(jì)分析。

從圖7 的關(guān)系曲線以及表7 的統(tǒng)計(jì)分析中,可得出以下結(jié)論:

表7 實(shí)測(cè)數(shù)據(jù)下選星前后對(duì)比分析Table 7 Comparative analysis before and after satellite selection based on field data

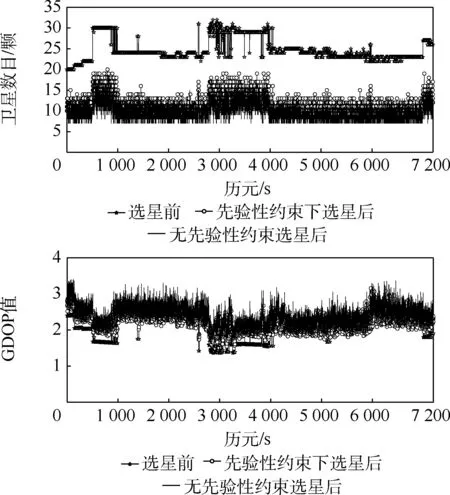
圖7 實(shí)測(cè)數(shù)據(jù)下選星前后對(duì)比Fig.7 Comparison of satellite selection before and after based on field data

1) 在實(shí)測(cè)數(shù)據(jù)下以及高度截止角選取為5°時(shí),本文算法在先驗(yàn)性約束下所選的平均衛(wèi)星數(shù)目較平均總衛(wèi)星顆數(shù)明顯降低,縮減率達(dá)45.4%,較無(wú)約束下的35.7%有所增加,但依舊可以大大降低衛(wèi)星數(shù)目。 同時(shí)由于采集的數(shù)據(jù)為2 h,衛(wèi)星總數(shù)總體變化趨勢(shì)較為平穩(wěn),但是本文算法選星后的衛(wèi)星數(shù)沒(méi)有固定,會(huì)發(fā)生變化,說(shuō)明可以靈活地進(jìn)行選星,比一般提前固定選星數(shù)目具有更強(qiáng)的機(jī)動(dòng)性。

2) 在實(shí)測(cè)數(shù)據(jù)下以及高度截止角選取為5°時(shí),在先驗(yàn)性約束下選星后的GDOP 平均值2.237 3相對(duì)于選星前的GDOP 平均值2.060 0 增加量小于0. 2,相對(duì)于無(wú)約束下平均GDOP 值2.485 7減少了0.248 4,說(shuō)明在實(shí)際采集的數(shù)據(jù)中,引入先驗(yàn)性約束后,本文算法能夠從全部可見(jiàn)衛(wèi)星中選取更多幾何構(gòu)型較好的衛(wèi)星,因此先驗(yàn)性約束下本文算法選星后的GDOP 值相對(duì)于選星前的GDOP 值依舊沒(méi)有發(fā)生太大變化,同時(shí)無(wú)論是否存在約束,選星后依舊將GDOP 控制在小于4 的范圍內(nèi),滿(mǎn)足用戶(hù)精度要求,說(shuō)明本文算法具有有效性。

同時(shí)基于每一歷元先驗(yàn)性約束選星后與選星前GDOP 的差值,對(duì)其進(jìn)行統(tǒng)計(jì)分析,如表8所示。

表8 實(shí)測(cè)數(shù)據(jù)下,選星前和先驗(yàn)性約束下選星后GDOP 差值在各區(qū)間下百分比Table 8 Percentage of GDOP difference before and after satellite selection with a priori constraint in each interval based on field data

與仿真情況下一致,本文將實(shí)測(cè)數(shù)據(jù)下每次選星前后GDOP 差值劃為[ -0.4, -0.2),[ -0.2,0),[0,0.2),[0.2,0.4),[0.4,0.5]5 個(gè)區(qū)間,由表8可知,在實(shí)測(cè)數(shù)據(jù)下選星前后GDOP 差值有17.78%落在[ -0.2,0)區(qū)間下,說(shuō)明實(shí)測(cè)數(shù)據(jù)中全部可見(jiàn)衛(wèi)星中存在著幾何構(gòu)型差的衛(wèi)星,從而選星后的可見(jiàn)衛(wèi)星的衛(wèi)星星座較選星前的衛(wèi)星星座幾何構(gòu)型好,進(jìn)一步說(shuō)明引入可見(jiàn)衛(wèi)星的衛(wèi)星仰角和方向角先驗(yàn)信息后,進(jìn)行先驗(yàn)性約束,能夠在一定程度上改善選星后的可見(jiàn)衛(wèi)星星座的幾何構(gòu)型。 所有的差值中最大差值依舊都小于0.5,說(shuō)明選星后的GDOP 值總體上與選星前的GDOP值相差不大,在精度要求范圍內(nèi)。 同時(shí),選星前后的GDOP 差值方差依舊較小,表明在實(shí)測(cè)數(shù)據(jù)下運(yùn)用本文算法時(shí),本文算法依舊比較穩(wěn)定。 因此,本文算法無(wú)論仿真還是實(shí)測(cè)數(shù)據(jù)下,都具有較強(qiáng)的有效性。

3.2.2 實(shí)時(shí)性分析

實(shí)測(cè)數(shù)據(jù)高度截止角5°下引入先驗(yàn)性約束和無(wú)約束下的單次選星耗時(shí)如圖8 所示,表9 為統(tǒng)計(jì)分析。

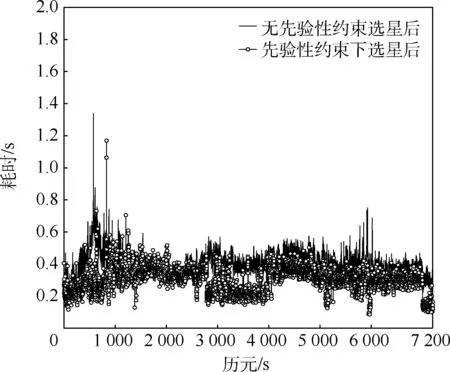
圖8 實(shí)測(cè)數(shù)據(jù)下有/無(wú)先驗(yàn)性約束單次選星耗時(shí)Fig.8 Time consumption of one-time satellite selection with/without prior constraint based on field data

由表9 可知,本文算法單次選星實(shí)際運(yùn)用時(shí),引入先驗(yàn)性約束后平均耗時(shí)0.303 1 s 依舊小于無(wú)約束下的平均耗時(shí)0.400 8 s。 因此,引入先驗(yàn)性約束后的耗時(shí)少于無(wú)約束下的耗時(shí),同時(shí)耗時(shí)方差較小,說(shuō)明本文算法實(shí)際運(yùn)用過(guò)程中,耗時(shí)穩(wěn)定,在具有良好的實(shí)時(shí)性的同時(shí)仍然保持著較強(qiáng)的有效性。

表9 實(shí)測(cè)數(shù)據(jù)下有/無(wú)先驗(yàn)性約束單次選星耗時(shí)數(shù)據(jù)統(tǒng)計(jì)Table 9 Statistics of time consumption for one-time satellite selection with/without prior constraint based on field data

4 結(jié) 論

本文設(shè)計(jì)了基于帝國(guó)競(jìng)爭(zhēng)優(yōu)化的雙目標(biāo)綜合決策選星算法,為了選取幾何構(gòu)型較好的衛(wèi)星星座,引入衛(wèi)星仰角和衛(wèi)星高度角先驗(yàn)信息后,進(jìn)行先驗(yàn)性約束,同時(shí)通過(guò)構(gòu)建GDOP 和選星數(shù)目這2 個(gè)目標(biāo)進(jìn)行綜合決策實(shí)現(xiàn)了選星。 實(shí)驗(yàn)結(jié)果證明了在24 h 仿真數(shù)據(jù)和2 h 實(shí)測(cè)數(shù)據(jù)下進(jìn)行先驗(yàn)性約束后,本文算法不僅充分降低了衛(wèi)星數(shù)目,選星后依舊滿(mǎn)足用戶(hù)定位精度要求,同時(shí)選星后的GDOP 值較無(wú)約束下的GDOP 值有所減小,改善了所選衛(wèi)星星座的幾何構(gòu)型。 24 h 仿真以及2 h實(shí)測(cè)數(shù)據(jù)驗(yàn)證表明如下:

1) 本文算法在24 h 仿真時(shí)間高度截止角5°下,引入先驗(yàn)性約束后的所選平均衛(wèi)星數(shù)目近似于最大可見(jiàn)衛(wèi)星平均數(shù)目的51.8%,同時(shí)在2 h實(shí)測(cè)數(shù)據(jù)下為總可見(jiàn)衛(wèi)星數(shù)目平均數(shù)的52.4%,說(shuō)明本文算法有效降低了衛(wèi)星數(shù)目。

2) 本文算法在24 h 仿真數(shù)據(jù)以及2 h 實(shí)測(cè)數(shù)據(jù)下,引入先驗(yàn)性約束選星后的GDOP 值與總可見(jiàn)衛(wèi)星數(shù)目的GDOP 值差值最大值都小于0.5,且差值方差小,說(shuō)明選星前后的GDOP 差別不大,以及選星后的最大GDOP 依舊不超過(guò)4,能夠滿(mǎn)足用戶(hù)定位精度要求。 因此,綜合本文算法無(wú)論是仿真還是實(shí)測(cè)數(shù)據(jù)下,引入先驗(yàn)性約束后選星前后GDOP 變化較小以及衛(wèi)星數(shù)目降低,可以說(shuō)明在先驗(yàn)性約束下本文算法具有較強(qiáng)的有效性。

3) 本文算法在24 h 仿真時(shí)間下,先驗(yàn)性約束下單次選星平均所用時(shí)間約為0.168 4 s,相對(duì)于傳統(tǒng)遍歷法的4 s 所用時(shí)間優(yōu)化了95.79%,說(shuō)明本文算法具有較強(qiáng)的實(shí)時(shí)性。