初中數(shù)學(xué)動(dòng)態(tài)思維能力的培養(yǎng)

李雍金

摘要：面對(duì)動(dòng)態(tài)問(wèn)題，學(xué)生普遍感到困難，教學(xué)中要注意動(dòng)態(tài)思維的培養(yǎng)，提高解答動(dòng)態(tài)問(wèn)題的能力.初中每個(gè)學(xué)段對(duì)動(dòng)態(tài)問(wèn)題都有描述，用好這些素材，能鍛煉數(shù)學(xué)思想，培養(yǎng)學(xué)生的動(dòng)態(tài)思維能力，創(chuàng)造性地使用所學(xué)知識(shí)，有效解決復(fù)雜的動(dòng)態(tài)問(wèn)題。

關(guān)鍵詞：動(dòng)態(tài)思維;動(dòng)態(tài)問(wèn)題;能力;素材

動(dòng)態(tài)問(wèn)題在初中數(shù)學(xué)中占有重要位置，滲透運(yùn)動(dòng)變化的觀點(diǎn).這類題靈活性強(qiáng)、有區(qū)分度，能力要求高，它能全面的考查學(xué)生的實(shí)踐操作能力，空間想象能力以及分析問(wèn)題和解決問(wèn)題的能力，受到了人們的高度關(guān)注;同時(shí)，也得到了命題者的青睞.面對(duì)動(dòng)態(tài)問(wèn)題，學(xué)生普遍感到困難，因此，在平時(shí)的教學(xué)中要注意對(duì)動(dòng)態(tài)思維的培養(yǎng)，提高解答動(dòng)態(tài)問(wèn)題的能力.本文結(jié)合教材，談動(dòng)態(tài)思維能力的培養(yǎng)。

一、靜中導(dǎo)動(dòng) 激發(fā)動(dòng)態(tài)思維

《標(biāo)準(zhǔn)》關(guān)于“數(shù)學(xué)思考”的課程目標(biāo)對(duì)初中生的要求：應(yīng)當(dāng)包括既能夠有數(shù)和簡(jiǎn)單的圖表刻畫一些現(xiàn)實(shí)生活中的現(xiàn)象，對(duì)某些數(shù)字信息作出合理的解釋，又能夠用各種數(shù)學(xué)關(guān)系（方程、不等式、函數(shù)等）去刻畫具體問(wèn)題，建立適合的數(shù)學(xué)模型.因此，教師要根據(jù)學(xué)生已有的知識(shí)，利用課本素材，引導(dǎo)學(xué)生對(duì)問(wèn)題進(jìn)行再思考.如：浙教版七年級(jí)（上）114頁(yè)例2：甲、乙兩人從A、B兩地同時(shí)出發(fā)，甲騎自行車，乙騎摩托車，沿同一條路線相向勻速行駛.出發(fā)后經(jīng)3小時(shí)兩人相遇.已知在相遇時(shí)乙比甲多行駛了90千米，相遇后經(jīng)1時(shí)乙到達(dá)A地.問(wèn)甲、乙行駛的速度分別是多少？

本例是一個(gè)靜態(tài)的數(shù)學(xué)問(wèn)題，會(huì)用方程的思想解答后，教師宜引導(dǎo)學(xué)生嘗試提出新的數(shù)學(xué)問(wèn)題，要求學(xué)生至少能提出下列三個(gè)問(wèn)題中的兩個(gè)問(wèn)題并解答：

①求A、B兩地的距離？

②甲、乙兩人出發(fā)1小時(shí)后，他們相距有多少千米？3.5小時(shí)時(shí)，又相距多少？

③求經(jīng)過(guò)幾小時(shí)后，兩人相距30千米？

顯然，提出問(wèn)題①是容易的，但卻體現(xiàn)了學(xué)生自主學(xué)習(xí)的一個(gè)過(guò)程;對(duì)類似于問(wèn)題②的提出，是學(xué)生自主探究、尋找發(fā)現(xiàn)問(wèn)題的結(jié)果.如果感到學(xué)生的困難，教師可畫圖做心理暗示，以激發(fā)學(xué)生的思維，由于有n個(gè)答案，教師把握分寸;問(wèn)題③是動(dòng)態(tài)思維的升華，利于教師發(fā)現(xiàn)數(shù)學(xué)人才.在這一過(guò)程中學(xué)生自覺(jué)與不自覺(jué)借助圖形幫助分析，使用數(shù)形結(jié)合的方法去尋找和發(fā)現(xiàn)問(wèn)題，鞏固加深對(duì)范例的理解，數(shù)學(xué)思維能力得到充分的發(fā)展，達(dá)到懂一題會(huì)一片的思維境界。

二、動(dòng)中取靜 發(fā)展動(dòng)態(tài)思維

《標(biāo)準(zhǔn)》關(guān)于“數(shù)學(xué)思考”的課程目標(biāo)對(duì)初中生又要求：經(jīng)歷觀察、實(shí)驗(yàn)、猜想、證明等數(shù)學(xué)活動(dòng)過(guò)程，發(fā)展合情推理能力和初步的演繹推理能力，能有條理地、清晰地闡述自己的觀點(diǎn).對(duì)于學(xué)生普遍感到棘手的動(dòng)態(tài)問(wèn)題，有時(shí)可交由學(xué)生合作完成，教材中也有安排.如：浙教版八年級(jí)（下）39頁(yè)的合作學(xué)習(xí)：

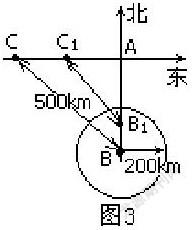
一輪船以30km/h的速度由西向東航行（如圖3），在途中接到臺(tái)風(fēng)警報(bào)，臺(tái)風(fēng)中心正以20km/h的速度由南向北移動(dòng).已知距臺(tái)風(fēng)中心200km區(qū)域（包括邊界）都屬于受臺(tái)風(fēng)影響區(qū).當(dāng)輪船接到臺(tái)風(fēng)警報(bào)時(shí)，測(cè)得BC=500km，BA=300km.如果輪船不改變航向，輪船會(huì)不會(huì)進(jìn)入臺(tái)風(fēng)影響區(qū)？你采用什么方法來(lái)判斷？

如果你認(rèn)為輪船會(huì)進(jìn)入臺(tái)風(fēng)影響區(qū)？從接到警報(bào)開(kāi)始，經(jīng)多少時(shí)間就進(jìn)入臺(tái)風(fēng)影響區(qū)？

素材中動(dòng)態(tài)問(wèn)題有代表性、挑戰(zhàn)性，學(xué)生對(duì)臺(tái)風(fēng)的影響雖然有一定的認(rèn)識(shí)，但同學(xué)感到有難度.船在動(dòng)，臺(tái)風(fēng)也在動(dòng)，左右著學(xué)生的思維，不能找到解答問(wèn)題的途徑，展開(kāi)合作學(xué)習(xí)是有必要的.合作學(xué)習(xí)要解決三個(gè)問(wèn)題①如何判斷輪船是否進(jìn)入臺(tái)風(fēng)影響區(qū);②BC的長(zhǎng)能計(jì)算嗎？③如果要計(jì)算BC的長(zhǎng)，如何排除BC隨時(shí)間的變化的影響.合作學(xué)習(xí)期間要關(guān)注①合作學(xué)習(xí)的進(jìn)展;②合作過(guò)程中有困惑嗎？③需要提示嗎？在這期間我邀請(qǐng)一位數(shù)學(xué)程度較好的同學(xué)與我一起模擬演示臺(tái)風(fēng)與輪船的運(yùn)行，并提示：運(yùn)動(dòng)到某一時(shí)刻時(shí)輪船與臺(tái)風(fēng)中心的位置固定嗎？如果是固定的，你能計(jì)算出此此時(shí)輪船與臺(tái)風(fēng)中心的距離嗎？以引導(dǎo)、啟發(fā)學(xué)生的思維.多重因素的影響下，學(xué)生的思路豁然開(kāi)朗，發(fā)現(xiàn)問(wèn)題的關(guān)鍵是提煉出Rt△AB1C1，即要捕捉到運(yùn)動(dòng)中的“靜態(tài)”瞬間，構(gòu)造出直角三角形，再利用勾股定理求出B1C1的長(zhǎng)與200進(jìn)行比較可解決問(wèn)題。

三、動(dòng)靜結(jié)合 提高動(dòng)態(tài)思維

《標(biāo)準(zhǔn)》關(guān)于初中“解決問(wèn)題”的課程目標(biāo)要求：形成解決問(wèn)題的一些基本策略，體驗(yàn)解決問(wèn)題策略的多樣性，發(fā)展實(shí)踐能力與創(chuàng)新精神.有了前兩個(gè)學(xué)年的學(xué)習(xí)經(jīng)歷，對(duì)于動(dòng)態(tài)問(wèn)題具備了一些基本的解題策略，為九年級(jí)進(jìn)一步學(xué)習(xí)動(dòng)態(tài)問(wèn)題打下了基礎(chǔ).為形成和提高學(xué)生的動(dòng)態(tài)思維，使學(xué)生在這一階段能夠獨(dú)立地解決動(dòng)態(tài)類問(wèn)題，創(chuàng)造性地使用所學(xué)習(xí)的知識(shí).如浙教版九年級(jí)（上）46頁(yè)例2：

如圖5，B船位于A船正東26km處.現(xiàn)在A、B兩船同時(shí)出發(fā)，A船以12km/h的速度朝正北方向行駛，B船以5 km/h的速度朝正西方向行駛.何時(shí)兩船相距最近？最近距離是多少？

本例，可以選擇動(dòng)與靜相結(jié)合的策略來(lái)解答，構(gòu)造圖形，捕捉Rt△AA/B/，是知識(shí)的再現(xiàn).學(xué)生自主利用勾股定理，用含有時(shí)間變量的代數(shù)式表示A/B/，如：設(shè)經(jīng)過(guò)t（h）后，A、B兩船分別到達(dá)A/、B/處，則兩船之間的距離為：A/B/=，但學(xué)習(xí)中學(xué)生沒(méi)能進(jìn)一步深入，沒(méi)能與所學(xué)的二次函數(shù)聯(lián)系起來(lái)，這說(shuō)明學(xué)生的創(chuàng)造性學(xué)習(xí)的能力不夠，抓住這一點(diǎn)，做提示：通過(guò)計(jì)算169t2-260t+676>0，就得到對(duì)應(yīng)A/B/的值，問(wèn)題自然得到解決。

動(dòng)與靜在一定條件下是能相互轉(zhuǎn)化的.當(dāng)遇到動(dòng)態(tài)問(wèn)題時(shí)，要善于動(dòng)中取靜，先把動(dòng)態(tài)問(wèn)題轉(zhuǎn)化為靜止?fàn)顟B(tài)來(lái)解決，然后再?gòu)撵o態(tài)轉(zhuǎn)到動(dòng)態(tài).這種動(dòng)態(tài)思維方式體現(xiàn)了由一般到特殊，再由特殊到一般的數(shù)學(xué)思想.這種動(dòng)態(tài)思維方式對(duì)解答類題具有指導(dǎo)作用。

數(shù)學(xué)課本是獲取數(shù)學(xué)知識(shí)的主要源泉，事實(shí)上，各地學(xué)業(yè)考試卷中絕大部分試題都是以課本的素材為原型加工改編的.因而“把握課程標(biāo)準(zhǔn)，以本為綱，緊扣教材”，從課本素材入手，探究相關(guān)的知識(shí)和結(jié)論，是提高解題能力與技巧、激活數(shù)學(xué)思維的重要途徑。

參考文獻(xiàn)：

[1]史炳星 劉曉玫 編著 《實(shí)施新課程精要讀本 初中數(shù)學(xué)》 首都師范大學(xué)出版社

[2]主編 盛建武 《新課程教學(xué)問(wèn)題解決實(shí)踐研究 初中數(shù)學(xué)》 中央民族大學(xué)出版社