試值代入法計算鹽水溶液的pH值

郝紹鵬

(金堆城鉬業股份有限公司化學分公司，陜西渭南，714000)

在教學、科研和化工生產中經常需要計算鹽水溶液的pH值，在已知各平衡常數和溶質濃度計算pH值時，通常采用消元整理后解關于[H+]一元高次方程。由于目前沒有精確表達高次方程根的方法，計算方法主要分為兩大類：一類是在解方程前先進行近似處理，然后由簡化的近似求解公式求解的粗略計算[1，2]；另一類是依托高次方程使用二分法、迭代法等并借助計算機進行精確計算[3，4]。近似公式求解采用了近似處理前置的處理方式，在缺乏大量實驗數據印證的情形下，無法評估其計算結果的偏差。二分法、迭代法進行精確計算時，將化學問題高度抽象成數學運算，不易感知計算過程與化學原理之間的聯系，同時采用此類方法需要較高的數學邏輯認知或專業軟件輔助，在實際應用中也不易實施。

若將[H+]也看作是已知值，代入所有過程等式，則各等式應全部成立。此時的計算過程是一組數字簡單、大量的混合運算以及數量比較，不再涉及復雜的高次方程解法。

1 計算原理

1.1 主要運算式

設有正鹽或酸式鹽MzZm的水溶液體系，堿離子Mm+進行n級水解，強堿鹽n=0，弱堿鹽n=m；陰離子Zz-全部以Xx-、Yy-及其水解產物的形式存在，Yy-發生y級水解；Xx-發生a級水解，同多酸根體系a=x，體系無同多酸根a=0；Xx-、Yy-、Zz-中特征元素原子個數分別為s、t、r(如碳酸根、碳酸氫根中的碳元素)。建立其物料平衡式(MBE)和電荷平衡式(CBE)，并將兩式中的各平衡濃度用[Xx-]、[Yy-]、[H+]表示，整理出方程組及其解的表達式；建立[Xx-]、[Yy-]之間關系式的通式(以下簡稱試算式)。如圖1。

圖1 主要算式及說明

對于給定的鹽，各參數和試算式確定。各平衡常數和溶質濃度已知時，每試選一個[H+]的猜測值，可算出方程組的解，代入試算式中可算出k的一個試算值(為了避免混淆，稱平衡常數k的實際值為目標常數，試值代入計算所得的k值稱為試算值)。與目標常數最接近的試算值所對應的[H+]猜測值，即為所要計算的氫離子平衡濃度，進而算得pH值。

1.2 試值選擇

分組選取pH值實現對[H+]的試值選擇。選取p組pH值，各組內pH值為等差數列，各組的公差依次減小且成等比數列，公比為1/q。第二組及其后各組均有2q-1個pH值，最后一組的公差小于所需精度，第一組結合第二組使全部選值可覆蓋pH值1至14。從第一組開始依次代入計算，選取最接近目標常數的試算值對應的pH值，作為后一組pH值的中位數。

第一組在理論pH值附近捕獲一個節點，其后各組在捕獲的節點附近提高計算精度并逼近理論值。上述選值中的重復取值，是為了便于文字描述和電子表格編輯，實際應用中可合理避免。

2 計算的實現

使用EXCEL電子表格作為工具，對水解不高于7級、pH值1至14范圍內的體系進行計算，計算流程、中間輔助計算值、主要函數公式見圖2。圖中指數差指試算值常用對數與目標常數常用對數的差的絕對值；獲得計算結果與獲取中位數所用函數相同，改變其計算單元格范圍即可。

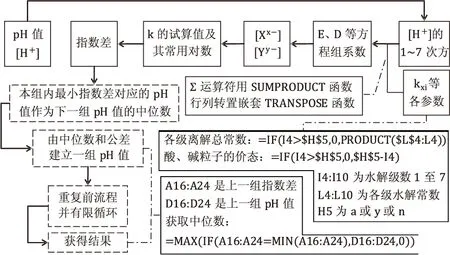
圖2 軟件計算流程示意圖

3 計算示例

示例中第一組9個pH值，中位數為7，公差1.458；各組公差之間的比例為3，共8組；pH值精度±0.000667。

3.1 同多酸鹽計算示例

鑒于同多酸鹽在水溶液中的平衡狀態比較復雜，這里將(NH4)6Mo7O24水溶液體系視為僅有兩種同多酸根，以此為模型介紹同多酸鹽水溶液pH值的計算，參數設置和水解見表1[5，6]。對1mol/l、0.1mol/l、0.01mol/l、0.001mol/l、0.0001mol/l(NH4)6Mo7O24水溶液pH值的計算結果分別約為5.855、5.461、5.045、4.614、4.26。

表1 同多酸鹽水解

3.2 正鹽、酸式鹽計算示例

分別以Na3PO4、Na2HPO4、NaH2PO4水溶液pH值的計算為例，參數設置和水解見表2[6]，計算結果見表3[1]。

表2 正鹽、酸式鹽水解

計算多元弱酸正鹽和酸式鹽水溶液的pH值，不僅可以獲得相對精確的結果，而且從計算過程可以觀察到一些現象。如表2中三種鹽的參數設置只有z(陰離子價態)不同，結合表3數據可知，濃度相同時，參數z的變化引起計算結果的變化。再如表3中，比較指數差可以發現，在相同精度內，NaH2PO4的指數差明顯較大；通過增加計算行提高計算精度，pH值精度達到約±3.76×10-9時，指數差分別為0.03(1mol/l)、0.06(0.01mol/l)、0.003(0.0001mol/l)。

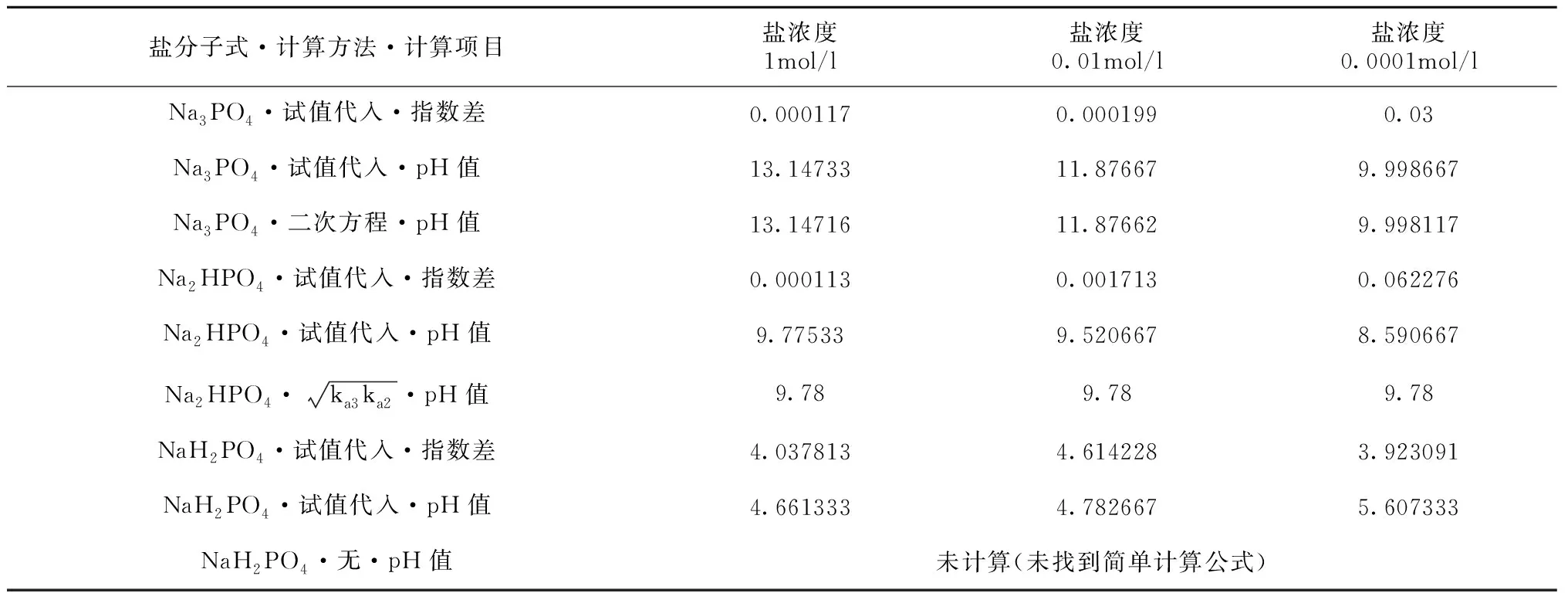
表3 正鹽、酸式鹽水溶液pH值計算對比

4 總結與結論

試值代入法為計算pH值提供了一種新的思路，將推導高次方程求根公式的難點轉化為大量簡單計算，再利用電子表格實現求值，獲得了良好的效果。

此方法計算范圍廣泛，可以完整地實現對正鹽、酸式鹽水溶液pH值的計算，可以嘗試對同多酸鹽水溶液pH值的計算。雖然在電子表格中的編輯和設置比較復雜，需要足夠的耐心和細致；但此方法的過程原理簡單，且可用日常辦公軟件實施，不需要高深的理論知識和專業軟件即可實現對pH值的高精度計算，仍然適用于廣大教學和技術研究人員使用。

除計算結果在所需精度內做近似處理外，計算過程中不做其他近似，完整考慮了水的離解和酸堿的各級水解，使計算結果獲得較高的精度。且從過程中可觀察到一些現象，如陰離子價態對pH值計算結果有影響；觀察指數差用以評估偏差等。