考慮轉動阻抗對砂力學特性影響的離散元分析

王 壯， 段志波， 廖新超， 劉一鳴

(湖北工業大學土木建筑與環境學院， 武漢 430068)

離散單元法由Cundall等[1]于1979年提出，是一種從細觀出發研究物質宏觀力學特性的方法，被廣泛應用于砂土方面的研究。基于離散元法，程升等[2]通過雙軸壓縮模擬試驗，對南海軟黏土的細觀參數進行了標定；史乃偉等[3]研究了臨界狀態下砂顆粒的運動狀態；蔣明鏡等[4]通過單粒組密砂的直剪模擬，分析了剪切帶形成的微觀機制。

傳統的離散單元模擬在生成大量顆粒來確保數值模型具有代表性的同時，為提高其模擬效率，將砂顆粒簡化為球形顆粒。顆粒之間的接觸作用常被認為僅發生在一個點上，主要由顆粒重疊產生的正向力和由顆粒之間相對滑動產生的切向力組成，忽略了顆粒轉動的影響[5]。這導致了顆粒尺度細節的損失，使顆粒集合體材料的剪切強度低于實際值。1982年Oda等[6]通過對橢圓顆粒進行雙軸壓縮試驗發現決定顆粒材料力學機制及微觀變形機制的主要因素為顆粒之間相對轉動作用。眾多學者為考慮顆粒間轉動的影響對離散元法進行了改良，并引入轉動阻抗的概念[6-9]。Iwashita等[7]進一步拓展了離散元接觸模型，在其基礎上計入轉動分量。Jiang等[8]提出了能完整反映無黏性材料力學行為的抗轉動線性接觸模型，設定顆粒間的接觸為面接觸，并考慮了轉動阻抗的影響。Jiang等[9]研究表明，將接觸力矩納入離散單元接觸模型可以有效地獲得更真實的體積強度，并識別顆粒材料的變形行為。Zhao等[10]綜合比較了滾動阻力和顆粒形狀對顆粒材料內部剪切誘發的織構變化和各向異性的影響，發現滾動阻力模型可有效再現砂土中剪切誘導各向異性的主要特征。轉動阻抗的作用不可忽視且與砂土的強度以及變形有著密切聯系。

基于上述分析，針對轉動阻抗對砂土強度影響的研究已取得了一定的成果，然而在轉動阻抗微觀影響機理方面研究較少，同時二維研究導致顆粒細節缺失。鑒于此，基于離散元法，通過顆粒流程序PFC3D5.0，采用不同抗轉動系數和不同圍壓進行三軸模擬試驗，分析轉動阻抗對砂土強度和變形的影響，分別從平均配位數、概率密度函數、顆粒間法向接觸力和各向異性的角度分析轉動阻抗的細觀影響機制。以期為考慮轉動阻抗因素的巖土類材料離散單元建模提供理論參考。

1 離散單元模型

1.1 本構模型

本構模型的選取對于數值模擬的準確性至關重要。本文研究采用了兩種本構模型，砂顆粒與墻之間的接觸為線性接觸模型，砂顆粒與砂顆粒間的接觸為抗轉動線性接觸模型，其原理如圖1所示。

圖1 接觸模型[3]

線性模型的接觸點可以想象為一對彈性彈簧，線性力由具有恒定法向剛度和切向剛度的線性彈簧產生，其力學原理為

(1)

(2)

在線性模型的基礎上，抗轉動線性接觸模型增加了轉動阻抗力矩[7]，其定義為

Mr=krθ

(3)

(4)

(5)

顆粒轉動控制方程為

(6)

內部力矩隨著接觸點處接觸件的累積相對旋轉而線性增加。這種累積的最大極限值等于當前法向力與抗轉動系數和有效接觸半徑的乘積。

(7)

1.2 數值模型

砂真三軸數值模擬試驗主要包括以下3個階段：①制樣階段，首先生成六面無摩擦剛性墻體，形成40 mm×40 mm×80 mm的長方體，然后在長方體內按孔隙率0.35生成顆粒，不平衡力比達到10-5時停止，以平衡制樣產生的初始內力；②固結階段，通過伺服程序控制六面無摩擦剛性墻體的相對移動，施加固結所需的目標圍壓；③剪切階段，在伺服機制保持一定圍壓的同時，通過控制上下兩面墻體的相對移動實現對試樣的剪切。

模擬試驗方案：砂試樣建模完成后控制變量，分別取圍壓為100、200、300 kPa，抗轉動系數取0、0.1、0.2、0.3和0.4，共計15組試樣，進行固結排水三軸剪切模擬試驗。數值模型如圖2所示，細觀參數的選取如表1所示。

圖2 砂真三軸數值模型

表1 數值模擬試驗參數

2 宏觀結果分析

圖3為圍壓σc=100 kPa條件下，不同抗轉動系數時偏應力-軸向應變曲線，各曲線初始階段基本呈直線且斜率一致，表明轉動阻抗對試樣初始彈性模量影響不大；隨著剪切進一步進行，偏應力相繼達到峰值，這是由于轉動阻抗抑制了砂顆粒間相對轉動，從而破壞面延后出現；達到峰值后，各曲線均表現出軟化現象，且抗轉動系數越大，軟化越明顯。

圖3 偏應力隨軸向應變變化曲線

圖4為偏應力峰值隨抗轉動系數變化曲線，可以看出：抗轉動系數和圍壓的增大，都會引起偏應力峰值增大；其中偏應力峰值增幅隨著抗轉動系數的增大而逐漸減小，表明轉動阻抗的影響逐漸趨于飽和。

圖4 偏應力峰值隨抗轉動系數變化曲線

圖5為100 kPa圍壓時體應變變化曲線，表現為先剪縮后剪漲，且轉動阻抗對剪脹現象有明顯增強作用。

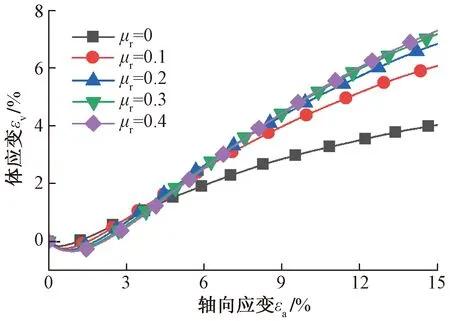
圖5 體應變隨軸向應變變化曲線

內摩擦角是衡量顆粒材料抗剪強度的重要指標[11]，采用峰值內摩擦角φs來衡量砂的強度，其定義為

(8)

式(8)中：σ1為大主應力；σ3為小主應力。

由圖6可知，試樣峰值內摩擦角均隨著抗轉動系數的增大而增大，且增長幅度逐漸減小，與蔣明鏡等[12]研究結果一致。

圖6 峰值內摩擦角隨抗轉動系數變化曲線

綜上所述，轉動阻抗可以有效地提高試樣的剪切強度，彌補傳統模擬試驗中將砂顆粒模擬為球體而導致抗剪強度低于實際值的缺陷。

3 細觀力學特性

3.1 力學配位數

配位數是試樣中某個顆粒與周圍顆粒的激活接觸數目，即法向接觸力大于零的接觸，是判斷顆粒材料內部穩定性的重要指標。一般采用平均配位數表征顆粒集合體材料內部顆粒的接觸狀態。本研究選用平均力學配位數[13]，其定義為

其次，合同文本的語句具有如下特征：第一，多用復雜長句以使語義表達更完整。第二，多用陳述句，因為陳述句可以更好地規定和說明商務合同雙方的責任和權利，避免歧義。第三，多使用被動語態，因為合同內容避免摻雜個人感情，被動語態能更客觀公正的表達。

(9)

式(9)中：Nc為試樣內部總接觸數：Ns為試樣內部總顆粒數；Ns0為某顆粒周圍無接觸的顆粒數；Ns1為某顆粒周圍接觸數目為1的顆粒數。

圖7為不同抗轉動系數下平均力學配位數隨軸向應變的變化曲線，曲線均呈現先微弱增加后下降至某一穩定值趨勢。圖7中配位數增加是由于試樣內部孔隙的壓縮，有效接觸變多；隨著剪切進一步進行，試樣發生剪脹，因此配位數降低；最終趨于穩定表明砂粒間形成了穩定的力鏈結構，有效接觸不再改變。抗轉動系數越大，曲線出現拐點時的軸向應變越大，且配位數的穩定值越小，這是由于轉動阻抗抑制了顆粒間的相對轉動，進而延后了穩定力鏈結構的形成，且減小了平均配位數。圍壓對于配位數的影響符合一般規律，圍壓越大，配位數越大。

圖7 配位數隨軸向應變變化曲線

3.2 概率密度

法向接觸力可以用概率密度函數(probability density function，PDF)進行統計量化。Azéma等[14]根據平均法向接觸力〈fn〉，將法向接觸力fn分為強、弱接觸力。對應的接觸力分別隨歸一法向接觸力fn/〈fn〉呈指數分布和近乎冪函數分布狀態，其表達形式為

(10)

式(10)中：α、β為擬合參數。

圖8反映了σc=100 kPa時峰值狀態下，轉動阻抗對法向接觸力概率密度分布的影響規律，從圖8(a)可知，不同抗轉動系數條件下概率密度均隨著法向接觸力的增大而減小，當法向接觸力較小時，轉動阻抗對其概率密度影響不明顯；而較大的法向接觸力的概率密度隨著抗轉動系數的增大而增大。

圖8 法向接觸力概率密度分布

圖9 不同抗轉動系數對應的擬合參數

3.3 法向接觸力

圖10為峰值狀態下平均法向接觸力隨抗轉動系數的演化曲線，由圖10可知，平均法向接觸力隨抗轉動系數增加呈增長趨勢，且圍壓越大，增長趨勢越明顯。

圖10 平均法向接觸力隨抗轉動系數變化曲線

法向接觸力的空間分布可以采用三維球面直方圖[15]直觀描繪。圖11中每一根棱條表示在其方向上的歸一化局部平均法向接觸力

圖11為100 kPa圍壓時各特征狀態下的三維直方圖，直觀反映了局部平均接觸力分別在初始狀態、峰值狀態和最終狀態的空間分布情況。初始狀態時，三維直方圖均近似球體，即法向接觸力基本表現為各向同性；峰值狀態時，球面直方圖沿豎向拉長，表示加載方向形成強接觸力，而隨著抗轉動系數的增大，球面直方圖更加細長，其尺度范圍隨之增大，表明抗轉動阻抗增大會增強其各向異性程度，使強接觸力抵抗軸向加載的能力更強；相比于峰值狀態，最終狀態較為粗短，即其各向異性在峰后呈現近似軟化趨勢。

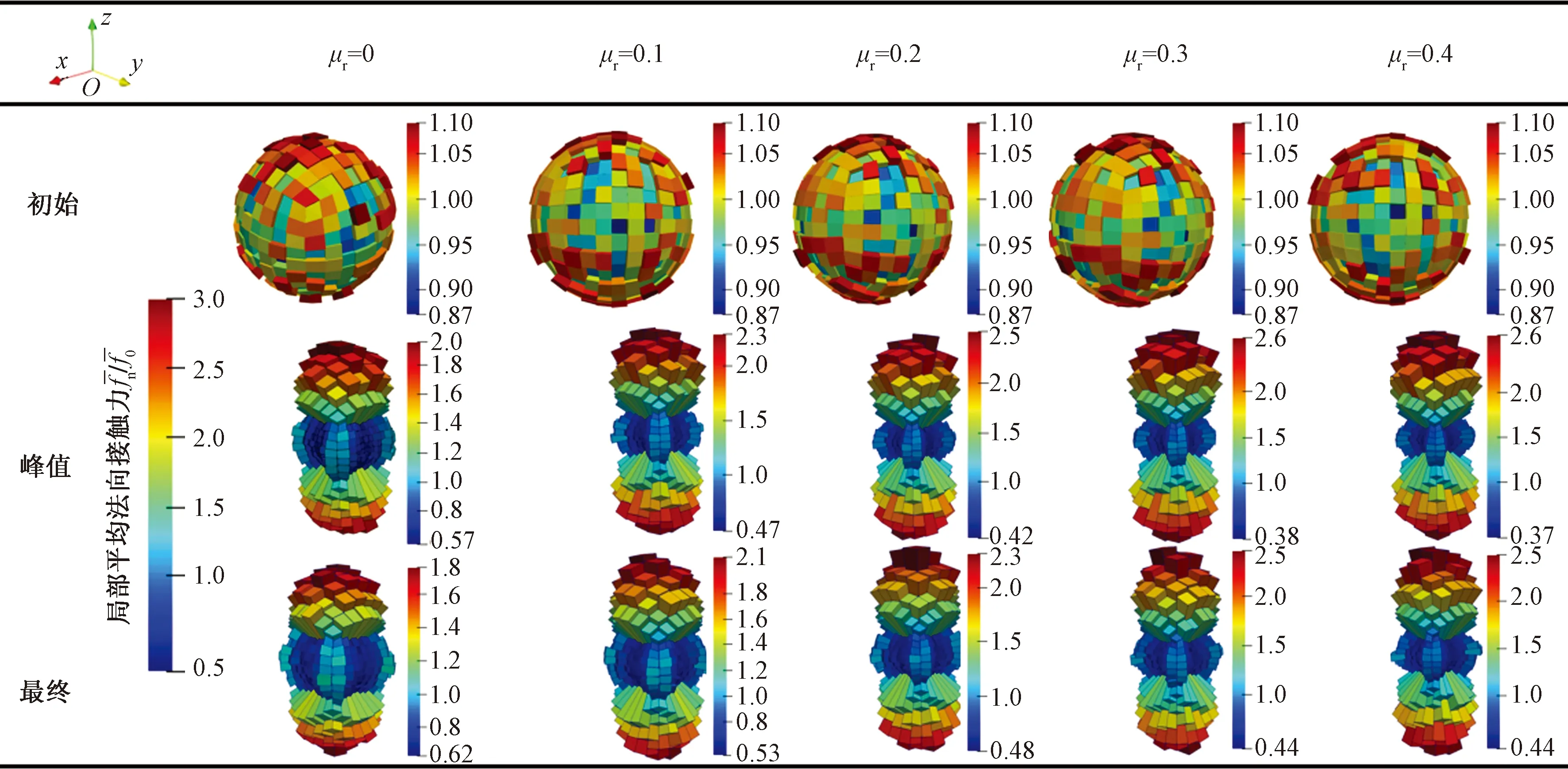
圖11 局部平均法向接觸力三維演化

3.4 各向異性

剪切導致砂顆粒間接觸狀態不斷變化，砂顆粒間的接觸重分布進而導致組構各向異性的演化。Oda[16]結合結構各向異性與排列密度定義了組構張量，通過分布密度函數E(Ω)和接觸法向各向異性系數ac來表征組構張量。

(11)

(12)

(13)

(14)

(15)

(16)

(17)

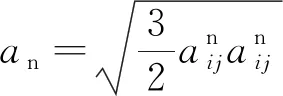
(18)

圖12和圖13分別為不同圍壓條件下，接觸法向各向異性系數(ac)和法向接觸力各向異性系數(an)隨軸向應變的變化曲線。剪切前期，由于試樣發生膨脹變形，ac和an的演化規律十分相似，均表現為急劇增加；達到峰值后，ac趨于穩定，這是由于試樣演化出的接觸法向各向異性程度達到上限，即試樣內部已經形成較為穩定的接觸結構，這與配位數最終趨于穩定相互匹配；而an隨剪切進一步進行顯示出軟化趨勢，且抗轉動系數越大，軟化趨勢越明顯，與應力應變規律相對應，表明法向接觸力對抗剪強度具有顯著的貢獻。對比圖12與圖13可知，整個剪切過程中，an均大于ac，這是由于法向接觸力大小的非均勻分布導致的。隨著抗轉動系數的增大，ac與an均隨之增大，且兩曲線拐點對應的軸向應變亦隨之增大，表明轉動阻抗增大了剪切誘導各向異性的演化程度，進而提高了砂的抗剪強度及穩定性。

圖12 接觸法向各向異性系數隨軸向應變變化曲線

圖13 法向接觸力各向異性系數隨軸向應變變化曲線

4 結論

(1)轉動阻抗對砂體強度及變形規律存在顯著的影響，隨著抗轉動系數增大，峰值強度及峰值內摩擦角均增大，試樣先剪縮后剪脹的變形特征更加顯著。宏觀結果與前人研究成果趨勢一致，驗證了本模型的可行性。

(2)轉動阻抗的作用降低了砂體的平均力學配位數，但同時增大了砂試樣內部強接觸力的概率密度及其大小，而強接觸力主要起抵抗外部荷載的作用，因此提高了砂的抗剪強度。

(3)隨著抗轉動系數的增大，接觸法向和法向接觸力各向異性均隨之增大，法向接觸力各向異性增強主要是強接觸力各向異性的增加。從而使砂土內部力鏈結構更加穩定。