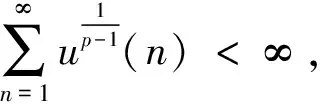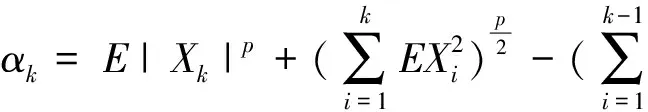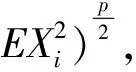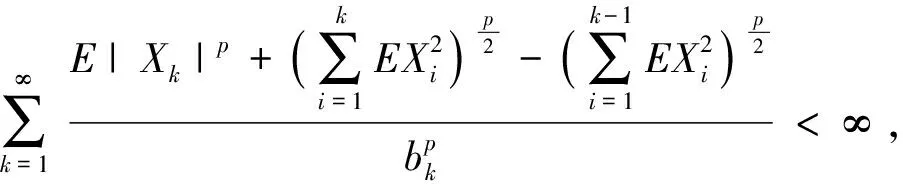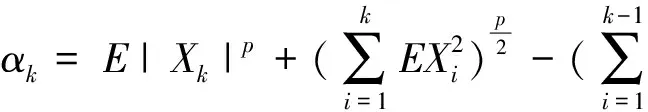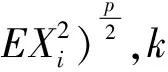AANA序列的Brunk-Prokhorov型強大數(shù)定律
馮德成,鄭 蕊,謝靜芳
(西北師范大學 數(shù)學與統(tǒng)計學院,蘭州 730070)
1 預備知識
隨機變量序列的極限理論是概率論研究的熱點.其中具有優(yōu)良性質(zhì)的獨立隨機變量序列的極限理論研究已經(jīng)十分成熟,但生活中絕大多數(shù)事物之間并非互不相關(guān),而是有某種聯(lián)系的.因此研究相依隨機變量序列的極限理論具有更重要的現(xiàn)實意義.
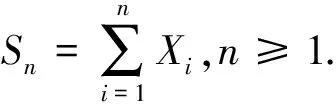
定義1設{Xn,n≥1}是一列隨機變量序列,如果存在一列非負數(shù)u(n)且u(n)→0(n→∞),使得
Cov(f(Xn),g(Xn+1,Xn+2,…,Xn+k))≤u(n)
則稱{Xn,n≥1}是AANA序列.這里n,k≥1且f,g是分量不減并且上述協(xié)方差存在的函數(shù).
定義2如果對{1,2,…,k}的任意每對非空不相交子集合A1,A2滿足
Cov(f1(Xi,i∈A1),f2(Xj,j∈A2))≤0[2],
則稱隨機變量X1,X2,…,Xk是NA的.其中f1,f2是使上式有意義的兩個非降函數(shù).進一步,稱隨機變量序列{Xn,n≥1}是NA序列,如果其任意有限子列是NA的.
相依隨機變量序列種類很多,AANA序列是一種有廣泛應用的相依序列.AANA序列的概念最早由Chandra等[3-4]給出,Chandra等得到了AANA序列的Kolmogorov型概率不等式、Marcinkiewicz-Zygmund型強大數(shù)定律及加權(quán)平均的幾乎處處收斂性,之后國內(nèi)外學者對AANA序列的研究更加深入.Ko等[5]得到了AANA序列的Hájek-Rényi型不等式;Wang等[6]推導出了AANA序列的乘積和的重對數(shù)律;Yuan等[7]又得到了AANA序列的Rosenthal型極大值不等式;Wang等[8]獲得了AANA序列的強增長律與部分和序列上確界的可積性.
強大數(shù)定律是相依隨機變量序列極限理論的重要課題,一直以來都是學者們關(guān)注的焦點問題.Brunk-Prokhorov強大數(shù)定律是強大數(shù)定律的一個重要組成.文獻[9-12]得到了一些相依隨機變量序列的Brunk-Prokhorov強大數(shù)定律.文獻[13]研究了PA(相協(xié))序列和NA序列的部分和序列在1 (1) (2) 引理3設{Xi,1≤i≤n}是均值為零的NA序列,p≥2.且對每一個1≤i≤n,有E|Xi|p<∞,則有 (3) 引理4設{Sn,n≥1}是一列隨機變量序列,{bn,n≥1}是一列不減的無界正數(shù)序列,{αn,n≥1}是非負數(shù)序列.r和C是固定的正數(shù).假定對每個n≥1有 則 并有增長率 這里 并且 (4) 此外如果假定對無限多個n,有αn>0,則 (5) 并有增長率 這里 并且 如果假定對無限多個n,有αn>0,則 這里,Dp與引理1中的Dp一致. 所以 取r=p,C=Dp,由引理4得 并有增長率 這里 由引理4中式(4)得 如果假定對無限多個n,有αn>0,由引理4中式(5)得 證畢. 下面證明當1 并有增長率 這里 并且 此外,如果假定對無限多個n,有αn>0,則 證明取αk=E|Xk|p,k為正整數(shù),則αk≥0.由引理2中式(2)得 因此 由引理4,定理得證. 證畢. 由定義得NA序列是特殊的AANA序列,下面給出在p≥2時NA序列的Brunk-Prokhorov型強大數(shù)定律. 并有增長率 這里 并且 此外,如果假定對無限多個n,有αn>0,則 所以 再由引理4,定理得證. 證畢.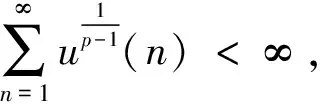
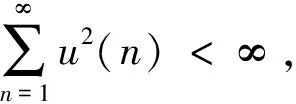
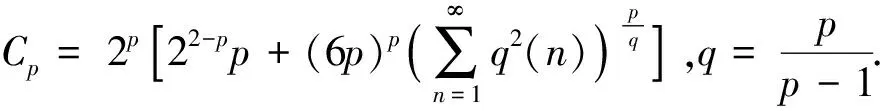
2 主要結(jié)論及證明