基于CFD模擬通道底部渠流的研究

陳文莉，翟朝凱，李萬祥

(蘭州交通大學 機電工程學院，蘭州 730070)

現實生活中，渠流底部是凹凸不平的，并不類似于簡單模型中那樣平滑，渠流底部障礙物的研究與人們的生活息息相關[1]，比如，黃河泛濫便是因為其底部泥水淤積，水流在底部迅速發生變化，進而影響河床形狀，最終引發黃河改道、決堤.通過對渠流底部障礙物更加真實的仿真模擬，從而對障礙物附近的流速變化得出更加精確的數據分析[2]，能夠為黃河流束水歸槽，防止河流潰泄決堤提供更加準確的參考依據.

通過使用STAR-CCM+軟件模擬在三維通道底壁上的障礙物的穩定氣流，通過模型設定、計算求解后得到了壓力云圖，速度云圖、以及壁面剪應力圖等.通過這些圖的分析對比，得出三維通道底壁上的障礙物參數，為渠流工況設計與研究提供理論依據.

1 參數計算

1.1 通道模型及參數設定

在STAR-CCM+中建立通道模型幾何圖，圖1所示參數為二維通道模型的基本參數，圖2、圖3為通道模型的二維及三維輪廓圖.通過進行劃分各個區域以及命名來進行邊界條件設定，把建立好的模型分配到區域中進行計算.空氣以標準壓力和溫度(1 bar和 293 K)進入解域，自由流速度設定為 1.17 m/s.[3-4]由于障礙物的高度為0.04 m，雷諾數為 3.115，從實驗數據可以測的渠流通道入口處的湍動能和湍流耗散率分別0.024 m2/s2和0.034 3 m2/s3.

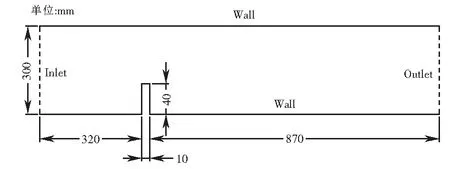
圖1 通道模型的基本參數Fig.1 The basic parameters of the channel model

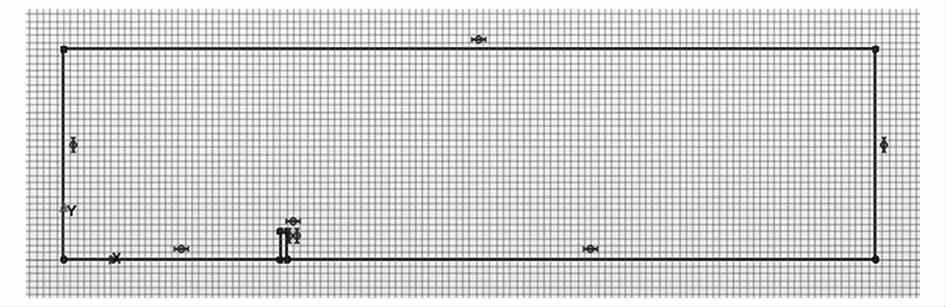
圖2 通道模型的輪廓Fig.2 The outline of the channel model

圖3 通道模型的三維圖Fig.3 A three-dimensional diagram of the channel model

1.2 表面離散化分析

對模型圖新建表面網格劃分，進行表面重構，通過設置面網格質量以及進行基礎尺寸的選擇，設定目標尺寸為外表面的尺寸，入口為300 mm2的正方形[5].最小表面尺寸要依據整個尺寸而設置，模型中最小值即障礙板的尺寸，障礙板尺寸為10 mm，采用20個網格捕捉，即每個網格為1 m的0.05%，面網格增長率為1.2，面網格如圖4所示.

對模型建立加密塊[6]，該加密塊區域尺寸可根據障礙板尺寸來確定，通過建立2個加密塊來更加直接的模擬氣流流動的方向.

圖4 離散化分析示意圖Fig.4 The face mesh is divided into schematics

加密塊1設置為障板前1 h,障板后13 h,障板上3 h，在Z軸方向貫穿.

加密塊2設置為障板前0.5 h，障板后3.5 h,障板上2 h,在Z軸方向貫穿.(其中h為障礙板高度，等于0.04 m)其中，加密塊2為最密的區域，加密塊1次之.

模擬結果如圖5所示.

圖5 加密塊位置示意圖Fig.5 An encrypted block location diagram

1.3 體網格加密設計

在體網格設置時，通過新建表面網格劃分，選擇表面重構以及需要的體網格生成器[7]，以切割體網格單元生成器進行論述，體網格增長率選用中等，設定體網格的最小尺寸.根據y+=30,可以確定障板第一層網格的厚度為0.48 mm，假設拉伸6層，由于體網格拉伸率為1.2，即棱柱層總厚度為4.77 mm.同理可得，壁面第一層厚度為0.95 mm，即棱柱層總厚度為9.43 mm，設定好尺寸即可得到體網格，如圖6所示.

圖6 體網格劃分示意圖Fig.6 A diagram of the body mesh division

2 三維流動模型CFD方法

三維通道底部壁上障礙物上的穩定氣流的模擬，采用三維不可壓縮定常湍流流動模型，湍流模型采用SST k-Omega模型[8-10].假定該流體流動是等溫、湍流且不可壓縮的，通過使用與Wolfstein兩層模型相結合的標準線性k-Omega模型模擬湍流.物理連續體中的湍動能的初始條件是0.024 J/Kg，湍流耗散率的初始條件為0.0343 m2/s3.

2.1 三維不可壓縮定常流動控制方程

三維通道底部壁上障礙物上的穩定氣流的模擬是三維不可壓縮定常湍流運動.依據質量守恒、動量守恒、能量守恒定律，可建立流動的控制方程[11]，具體方程如下：

連續性方程

(1)

動量方程

(2)

能量方程

(3)

理想氣體狀態方程

p=ρRT.

(4)

式中：ui(i=1,2,3)為速度分量；p為壓強；e為內能；R為摩爾氣體常數；

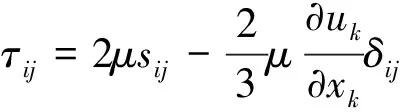
μ為動力粘性系數.

2.2 湍流模型控制方程

目前，湍流模擬方法有雷諾時均方法、大渦模擬和直接數值模擬三種方法.雷諾時均方法是工程常用的方法[12-13].本文采用雷諾時均方法SST k-ω模型.具體數學模型如下：

湍流動能k方程

(5)

湍流比耗散率ω方程

(6)

渦粘性系數定義為：

(7)

式中：Ω為渦量的絕對值.

(8)

(9)

(10)

(11)

(12)

式中：為距離下一表面的距離，是正擴散項.

(13)

(14)

(15)

SST k-Omega模型關系方程的系數見表1[14].

2.3 定解條件

2.3.1 初始條件

在時刻，通道周圍流場均靜止，各處壓力等于參考壓力，即一個標準大氣壓；溫度為298 K，湍流物理量也處處為零；入口流速為1.17 m/s，R=3.115，入口湍流能量為0.024 J/Kg，耗散率為0.034 3 m2/s3.即

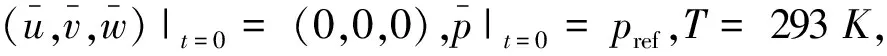
(16)

式中：Pref=101 325 Pa為遠場參考壓力.

2.3.2 邊界條件

通道模型的obstacle、ground、top、 rear表面為無滑移固體壁面， inlet、outlet表面為自由流邊界,front為對稱平面，具體見表2.

表1 SST k-Omega模型本構關系方程的系數

表2 傳輸變量

2.4 控制方程求解方法

本文采用基于有限體積方法的CFD軟件進行三維通道底部壁上障礙物上穩定氣流的數值模擬[14].使用同位網格的SIMPLE算法求解流動控制方程時，綜合考慮了電腦的設置，采用Rhie-Chow類壓力-速度耦合方法.代數方程組采用AMG方法求解[15].

3 網格設計

采用STAR-CCM+軟件中非結構化混合網格(Trim網格和Prism網格)對三維通道計算模型進行網格劃分.其中，內流場采用六面體網格(Trim網格)，壁面拉伸棱柱層網格(Prism網格).網格的基礎尺寸設置為0.3 m，最小相對尺寸設置為5.0%，相對目標尺寸設置為10%.在擋板附近設置兩塊大小不一樣的加密塊，第一塊加密塊的相對尺寸設置為1.0%，第二塊加密塊的相對尺寸設置為2.0%.

為了準確捕捉邊界層內的流動，本節對top、rear、obstacle和ground拉伸棱柱層網格.棱柱層網格設計過程中壁面y+、拉伸比和拉伸層數的選取必須遵循3個原則：首先，必須保證壁面處理方法的有效性；其次，邊界層內流場變量梯度較大，因此拉伸比不能太大；最后，保證最外層棱柱層網格與六面體網格有良好的過渡.通道模型的棱柱層網格具體設計情況如表3所示.

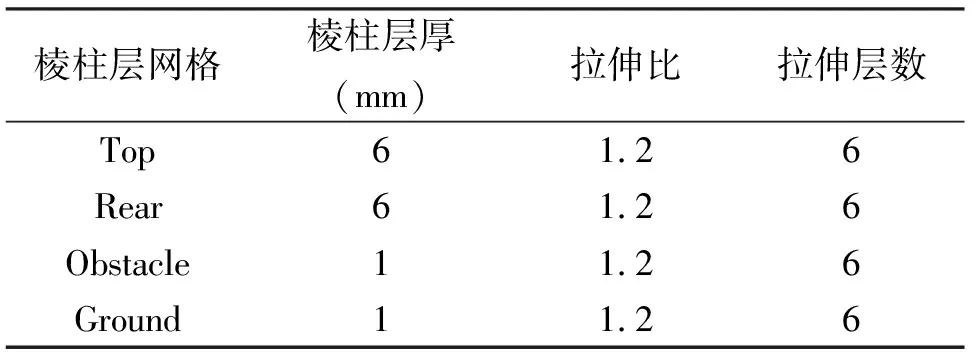
表3 棱柱層網格設計

在離散計算域時，考慮到擋板附近流場變化很大且容易形成漩渦結構，對這區域單獨加密.擋板附近到計算區域遠場空間，流場變化逐漸減小，因此在計算域內擋板附近到遠場采用網格逐漸由密變疏、均勻過渡的網格密度控制方法，這樣在保證計算精度的前提下，又能大幅度的減少網格數，降低對計算機內存的需求，從而提高計算效率，減少計算成本.圖7、8分別表示了加密塊設置的位置和擋板周圍加密塊展示效果圖.

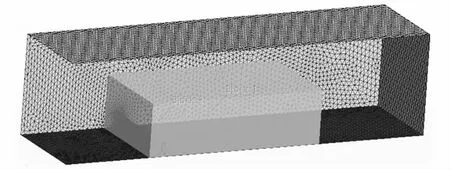
圖7 加密塊設置的位置Fig.7 Location of encryption block settings

圖8 加密塊展示Fig.8 Encrypted block display

4 后處理

由圖9可知，切割體網格單元分離器以及四面體、六面體網格分離器殘差均小于0.000 5且趨于穩定，所以該通道數值求解分析是收斂的.由圖10可以看出壁面y+值的分布；由圖11和圖12可以看出流體速度大小的分布；圖13、14分別是x-y plot圖.

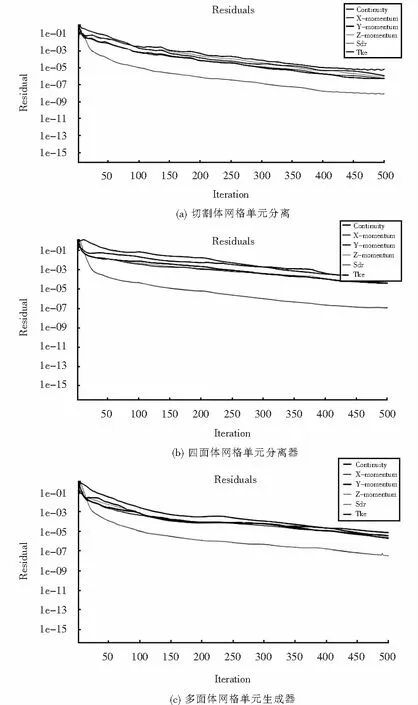
圖9 各類網格分布殘差圖Fig.9 Various grid distribution residual maps

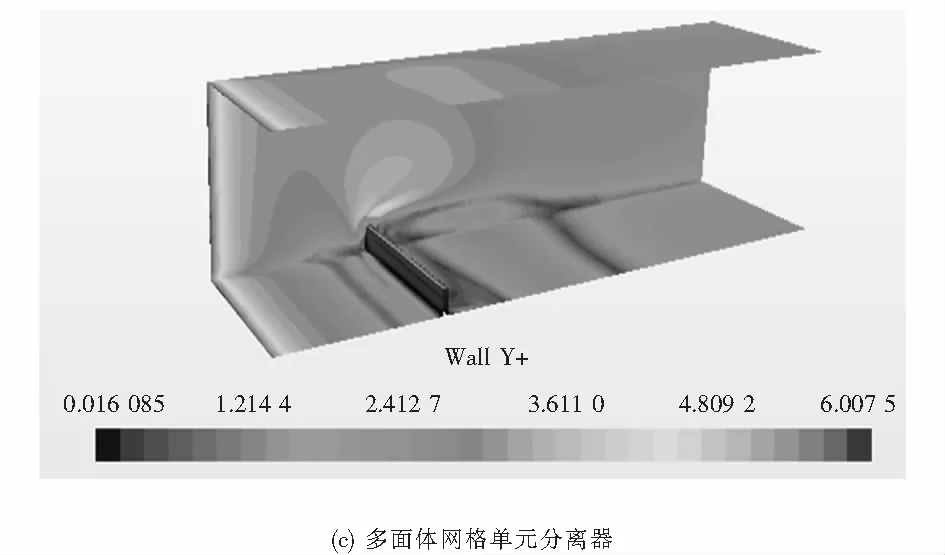
圖10 壁面y+的分布Fig.10 Distribution of wall y+

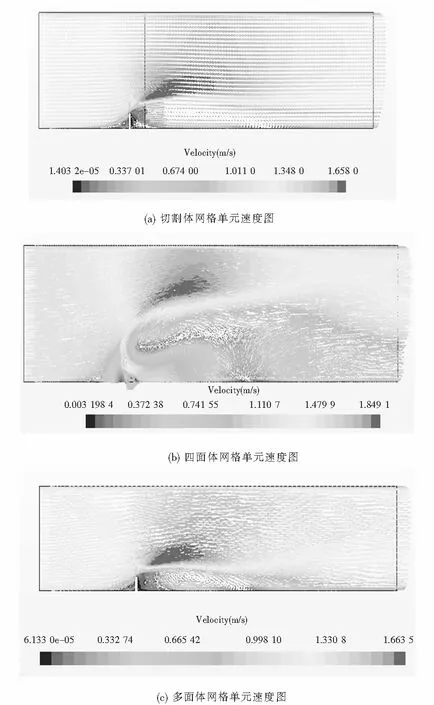
圖11 流體速度大小分布Fig.11 Fluid velocity distribution

5 三種網格的對比

切割體單元網格一共484 402個，內部面142 650個，節點總共537 929個.

四面體單元網格一共2 178 858個，內部面4 576 767個，節點總共561 281個.

六面體單元網格一共570 299個，內部面3 092 038個，節點總共2 295 145個.

圖12 流體速度大小分布卷積速度圖Fig.12 Convolution velocity diagram of fluid velocity size distribution

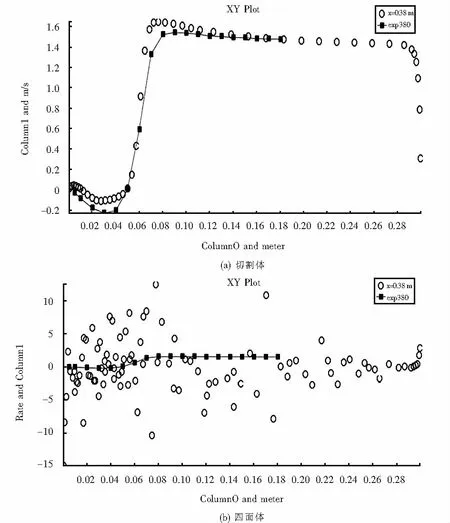
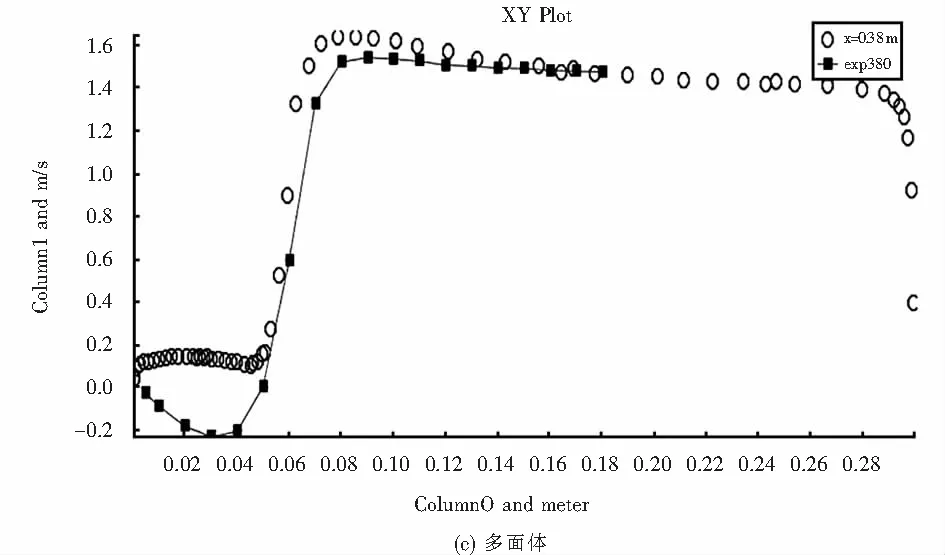
圖13 x=0.38 m速度剖面Fig.13 x=0.38 m Velocityprofile

圖14 壁面剪應力Fig.14 Wall shear stress

由此可以看出，四面體網格具有快速可靠的處理能力，允許復雜的幾何網絡具有較少的誤差，但結果的準確性較低.切割體網格主要利用六面體體積與最小的偏度和對齊與流動產生最高質量的網格.六面體網格具有比四面體網格和切割體網格更高的網格精度和網格質量.

6 結語

本文通過STAR-CCM+中三種不同網格對通道底部障礙物的穩定氣流進行模擬仿真分析，獲得較為準確的流體域中的流體速度大小分布流線圖、壁面y+分布圖、單元線積分卷積速度圖以及x-y plot圖等等.通過這些圖形的比對，可以得出三種網格有自己獨特的優缺點，四面體網格劃分簡單，但精度不高，且網格數量大.六面體網格劃分需耗費大量的時間，且對網格劃分經驗要求高，但網格數量較少，可節省計算時間且精度高，切割體網格主要利用六面體體積與最小的偏度和對齊與流動產生最高質量的網格.分析壓力、速度、剪應力等主要參數的分布，通過建立數學模型和對實驗數據的分析證明了物理模型和邊界條件的有效性.因此，通過對模型進行六面體網格離散化處理，可以獲得更加高的計算精度，分析結果可供工程實際檢算和設計參考，能夠對大型河道障礙物危害治理提供實踐指導作用.

由于CFD的方法具有成本低和能模擬較復雜工況并且具有較理想的過程的優點，在給定的參數下用計算機就能進行一次數值實驗，文中合理使用了CFD仿真技術進行氣流模擬，分析結果能夠為各類通道底部障礙物渠流工況企業以及對大型河道障礙物危害治理提供一定的指導作用.