含負項top-k高效用項集挖掘算法
孫 蕊,韓 萌,張春硯,申明堯,杜詩語
(北方民族大學計算機科學與工程學院,銀川 750021)
0 引言
近年來,數據挖掘技術引起了信息產業的極大關注。其中,頻繁項集挖掘是數據挖掘的重要組成部分之一。頻繁項集[1]的目標是發現滿足最小支持度閾值的所有項集。但是,在實際應用中,頻繁項集挖掘算法具有一定的局限性。它假定所有項具有相等的價值,并且每個項在每次事務中出現的次數不超過一次。但是,這兩個假設在現實生活中不是普遍存在的。例如,客戶購買6袋面包和1臺電腦,客戶購買多個相同的商品非常普遍,而出售面包和電腦的利潤卻有所不同。為了解決這一問題,研究人員提出了高效用項集挖掘算法。高效用項集(High Utility Iteme,HUI)[2]挖掘算法的主要目標是通過考慮用戶的偏好(例如利潤、數量和成本)來挖掘效用值高的項集。高效用項集挖掘算法克服了頻繁項集挖掘算法帶來的限制,在挖掘過程中,項的數量可能出現多次,并且每個項都有不同的價值。由于高效用項集挖掘算法缺乏向下閉合屬性,因此搜索空間很難縮小。隨后,Liu等[2]提出了一種Two-Phase算法,該算法使用向下閉合屬性來減小搜索空間,并有效地找到高效用項集。隨后,研究人員提出了IHUP(Incremental High Utility Pattern)[3]、TWU(Transaction Weighted Utility)-Mining[4]、IIDS(Isolated Items Discarding Strategy)[5]、UP-Growth(Utility Pattern Growth)[6]、UP-Growth+[7]算法。但是,以上提出的算法在挖掘過程中會生成大量的候選項集,這導致了算法執行時間長和內存消耗大的問題。Liu等[8]提出了一階段HUI-Miner(High Utility Itemset Miner)算法,該算法依賴效用列表結構,可以有效地修剪大部分搜索空間。
對于高效用項集挖掘算法,研究人員進行了許多研究。但是,絕大多數算法都是挖掘含有正效用的項集。在現實生活中,負效用項集也起著重要作用。例如,當客戶去超市購買計算機時,客戶可以免費獲得鍵盤和鼠標。假設超市從每臺計算機上獲利50美元,鍵盤和鼠標損失2美元,那么超市最終營利48美元。因此,負效用在現實生活中也具有重要意義。但是,大多數高效用項集挖掘算法都只挖掘正效用項集,如果用該類算法挖掘負效用項集,則會出現結果集遺漏問題。
針對傳統的高效用項集挖掘算法只能挖掘正效用項集的局限性,研究人員提出了挖掘單位利潤為負效用項集的算法。但是,在挖掘高效用項集時,最小效用閾值的設置問題始終是一個挑戰。如果最小效用閾值設置得太低,將產生大量的高效用項集,這將降低用戶使用效率;如果最小效用閾值設置得太高,將生成很少的高效用項集,這將無法滿足用戶的需求;反復調整最小效用閾值將花費大量的時間。
為了克服這些局限,本文提出了含負項top-k高效用項集(Top-kHigh utility itemsets with Negative items,THN)挖掘算法。該算法不需要設置最小效用閾值,只需要設置k值,就能得到用戶需求效用值最高的項集結果集合。本文的主要工作如下:
1)提出含負項top-k高效用項集挖掘算法——THN,該算法可以解決在挖掘同時含有正項和負項項集時需要設置最小效用閾值的問題;
2)該算法采用模式增長方法,使用重新定義的子樹效用和重新定義的本地效用修剪大量沒有希望的候選項集;該算法利用事務合并和數據集投影技術,提高了算法的時空性能;為了加快效用計數過程,該算法利用效用數組計數技術計算項集效用;
3)該算法提出了自動提升最小效用閾值的策略,實驗結果表明,該策略可以明顯減少算法的執行時間。
1 相關工作
目前,國內外研究者對含負項高效用項集挖掘算法和top-k高效用項集挖掘算法進行了研究。
1.1 含負項高效用項集
針對傳統的高效用項集挖掘算法只能挖掘含正項集的局限性,2009年Chu等[9]提出含負項的高效用項集挖掘算法HUINIV(High Utility Itemsets with Negative Item Values)-Mine。HUINIV-Mine算法是Two-Phase算法的擴展,它需要在內存中維護大量的項集,因此這嚴重影響了算法的效率。2011年,Li等[10]提出了MHUI-BIT(Mining High-Utility Itemsets based on BITvector)、MHUI-TID(Mining High-Utility Itemsets based on TIDlist)算法來挖掘含負項的高效用項集。但是,該算法還是存在產生候選項集過多的問題。Lin等[11]隨后提出了FHN(Faster High utility itemset miner with Negative unit profits)算法,該算法使用深度優先的搜索策略,并使用基于效用列表的EUCS(Estimated Utility Co-occurrence Structure)來有效地修剪搜索空間。實驗結果表明,FHN算法的執行時間是HUINIVMine算法的1/500,內存消耗是它的1/250。2014年,Lan等[12]提出了TS-HOUN(Three-Scan mining approach to efficiently find High On-shelf Utility itemset with Negative profit values)算法,該算法提出挖掘同時考慮貨架時間和含負項集的高效用項集。TS-HOUN算法采用三階段挖掘方法,在每個時間段挖掘項集,然后使用合并操作合并每個時間段的項集。由于多次掃描數據集,因此TS-HOUN效率很低。
為了解決多次掃描數據集的問題,FOSHU(Faster On-Shelf High Utility itemset miner)[13]算法使用了基于效用列表的結構,該結構同時挖掘所有時間段的項集。實驗結果表明,FOSHU算法的執行時間是TS-HOUN算法的千分之一,FOSHU算法的內存消耗是TS-HOUN算法的十分之一。2017年,Dam等[14]提出了FOSHU的擴展算法KOSHU(top-KOn-Shelf High Utility itemset miner)。2015年,Subramanian等[15]提出 了UP-GNIV(Utility Pattern-Growth approach for Negative Item Values)算法來挖掘含負項的高效用項集。2017年,Xu等[16]提出了HUSP-NIV(High Utility Sequential Patterns with Negative Item Values)算法,該算法用于挖掘含負項的高效用序列項集。2017年,Krishnamoorthy等[17]提出挖掘含負項的高效用項集挖掘算法——GHUM(Generalized High Utility Mining),GHUM比FHN快一個數量級。2017年,Gan等[18]提出 了HUPNU(High Utility patterns with both Positive and Negative unit profits from Uncertain data)算法,用于從不確定數據集中挖掘含負項的高效用項集。2018年,Singh等[19]提出了EHIN(Efficient High-utility Itemsets mining with Negative utility)算法來挖掘含負項的高效用項集,EHIN算法提出了多種有效的數據結構和修剪策略。同年,Singh等[20]提出了CHN(Closed High utility itemsets mining with Negative utility)算法來挖掘含負項閉合高效用項集。2019年,Singh等[21]提出了EHNL(Efficient High utility itemsets mining with Negative utility and Length constraints)算法來挖掘含負項和長度約束的高效用項集。
盡管上述所有的算法都可以挖掘含負項的高效用項集,但是難以解決挖掘出滿足用戶需求的高效用項集數量的問題。
1.2 top-k高效用項集
top-k高效用項集挖掘算法不需要設置最小效用閾值,直接根據用戶設置的高效用項集數量k進行挖掘。最早的top-k高效用項集挖掘算法是TKU(Top-KUtility itemsets mining)[22],它是UP-Growth算法的擴展。TKU算法采用Two-Phase模型:在第一階段,該算法使用多種策略來提高內部的最小效用閾值,并對搜索空間進行修剪,生成潛在的top-k高效用項集;在第二階段,從潛在的top-k高效用項集集合中識別真正的top-k高效用項集。TKU算法使用SE(Sorting candidates and raising threshold by the Exact utility of candidates)策略對候選項集進行排序并提高內部最小效用閾值。為了提高TKU的性能,Ryang等[23]提出了一種名為REPT(Raising threshold with Exact and Pre-calculated utilities for Top-khigh utility pattern mining)的算法,REPT算法依賴于UP(Utility Pattern)-Tree結構,通過使用額外的策略來快速提高邊界最小效用閾值,從而提高TKU的性能。由于TKU和REPT算法遵循Two-Phase模型,所以它們仍然產生了大量的候選項集。Zihayat等[24]提出了T-HUDS(Top-kHigh Utility patterns over sliding windows of a Data Stream)算法,用于在數據流上挖掘top-k高效用項集,THUDS提出了一種新的前綴效用模型,該模型采用HUDS(High Utility patterns over sliding windows of a Data Stream)-tree的壓縮數據結構。陳明福[25]提出了縮小候選項集TKDC(Top-Kpattern mining with Decreased Candidate)算法,該算法節省了大量的運行時間。
為了克服兩階段算法的局限性,研究者提出了一階段高效用項集挖掘算法。Lu等[26]提出了在數據流中挖掘top-k高效用項集的TOPK-SW(Sliding Window based TOP-K)算法,該算法將每批數據存儲在當前窗口中,并將項的效用信息存儲在HUI-Tree中,而無需再次掃描數據集。王樂等[27]提出了一種TOPKHUP(TOP-kHigh Utility Pattern)算法,該算法有效地將項集和項集效用信息保存到HUP-Tree中,從而確保可以直接挖掘top-k高效用項集。Tseng等[28]提出了TKO(Top-Kutility itemsets in One phase)算法來挖掘top-k高效用項集,TKO利用了HUI-Miner的效用列表結構,還提出了新的剪枝策略RUC(Raising the threshold by the Utilities of Candidates)、RUZ(Reducing estimated Utility values by using Z-elements)和EPB(Exploring the most Promising Branches first)來提高算法的性能。實驗結果表明,該算法的性能優于TKU和REPT算法。Duong等[29]提出一階段算法kHMC(top-kHigh utility itemset Mining using Co-occurrence pruning),它依賴于效用列表結構,采用多種策略提升最小效用閾值。Singh等[30]提出了TKEH(Efficient algorithm for mining Top-KHigh utility itemsets)算法,該算法使用事務合并和數據集投影技術來降低數據集掃描的成本。Kumari等[31]提出了TKRHU(Top-KRegular High Utility itemset)算法,該算法使用RUL(Regular Utility-Lists)效用列表結構來存儲每個規則表的規則信息和效用信息。Krishnamoorthy等[32]提出THUI(top-kHigh Utility Itemset)高效用項集挖掘算法,該算法使用LIU(Leaf Itemset Utility)結構來提高挖掘效率。實驗結果表明,在大型、密集和事務平均長度較長的數據集上具有更好的性能。
top-k高效用項集挖掘算法雖然可以不需要設置最小效用閾值就可以挖掘出用戶需求的高效用項集的數量,但是目前還沒有出現top-k高效用項集挖掘算法挖掘含負項的項集。
2 基本概念
事務數據集D由眾多事務組成,每條事務包含一些項,每條事務都由唯一的事務標識符Tid表示。I={i1,i2,…,in}指的是出現在事務數據集D中的不同項的集合。如表1所示,事務數據集D包含7條事務D={T1,T2,…,T7}和5個項I={A,B,C,D,E}。事務Tj∈D中項x的內部效用指的是事務Tj中x的數量,表示為IU(x,Tj)。事務Tj∈D中項x的外部效用指的是事務Tj中x的利潤,表示為EU(x)。如表1所示,事務T1中項A的內部效用為2;表2顯示了項的外部效用值,其中項A的外部效用值為2。

表1 事務數據集Tab.1 Transaction dataset
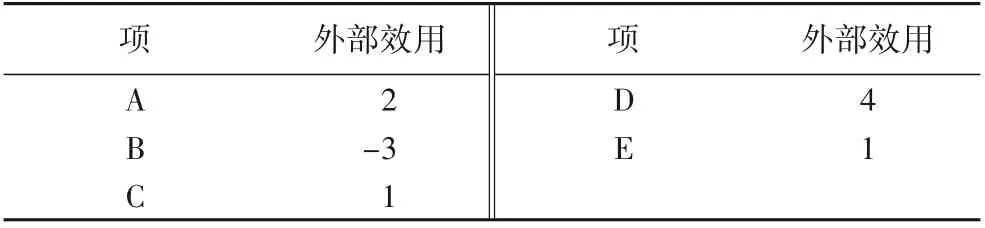
表2 外部效用值Tab.2 External utility values
定義1 項在事務中的效用[2]。項x在事務Tj中的效用定義為U(x,Tj)=IU(x,Tj)×EU(x)。
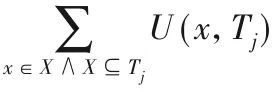
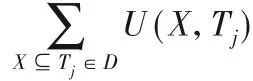
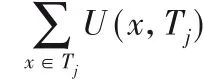
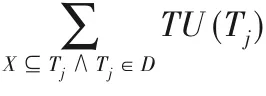
例如,TWU(D)=TU(D,T1)+TU(D,T3)+TU(D,T4)+TU(D,T6)=5+9+9+14=37。
定義6 高效用項集[2]。假定min_util是用戶設置的最小效用閾值。如果項集X的效用值不小于min_util,則項集X是高效用項集;否則,它是一個低效用項集。
定義7 top-k高效用項集[22]。按照項集效用值從高到低的順序排序,令min_util為第k個項集的效用值。對于項集X,如果條件項集X的效用值不小于min_util,則項集X稱為top-k高效用項集。
2.1 負項的屬性和定義
在傳統的高效用項集挖掘算法中,大多數都是挖掘含有正項的項集。但是,挖掘含有負項的高效用項集時,研究者提出了幾種處理負項集的屬性和定義。
屬性1 項集中的正效用和負效用之間的關系[9]。對于任何項集X,假定putil(X)表示事務或數據集中項集X的正效用之和,并假定nutil(X)表示事務或數據集中項集X的負效用之和。U(X)=putil(X)+nutil(X)。從以上屬性可以得到,putil(X)≥U(X)≥nutil(X)。
基本原理 項集X中效用值為正的項只能提高項集X的效用,而效用值為負的項只能降低項集X的效用。因此,屬性putil(X)≥U(X)≥nutil(X)成立。
屬性2 使用正效用對項集的效用上限[9]。項集X的效用上限為putil(X)。
基本原理 因為U(X)=putil(X)+nutil(X),而nutil(X)是要減小U(X),所以上述推理成立。
傳統的高效用項集挖掘算法使用TWU屬性來修剪搜索空間。但是,TWU屬性不能修剪含有負項的項集,因為TWU屬性假定修剪時不存在含有負項。為了解決這一挑戰,HUINIV-Mine[9]重新定義了相關概念。

例如,事務T2的重新定義的事務效用為RTU(T2)=U(C,T2)+U(E,T2)=5+1=6。通過添加僅計算重新定義的事務效用的項來增加了正項效果。表4顯示了每條事務的事務效用和重新定義的事務效用。

表4 事務效用和重新定義的事務效用Tab.4 Transaction utility and redefined transaction utility
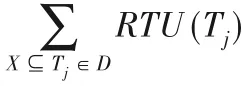
例如,RTWU(A)=RTU(A,T1)+RTU(A,T5)+RTU(A,T6)=11+4+17=32。
使用重新定義的事務加權效用修剪搜索空間,可以找到含負項高效用項集的完整高效用項集。事務中的項按總順序排序,因為RTWU按升序排序。
定義10 項集的擴展[19]。如果Y=α∪{X}(其中X∈2E(α),X不能為空),則項集α可以擴展為項集Y(Y出現在集合枚舉樹的重新定義的子樹中)。另外,項集α擴展了單個項集Y(Y是集合枚舉樹中α的子代)。其中X∈E(α),Y=α∪{X}。在運行的示例中,α={B},集合E(α)為{C,D},詞典α的單項展開為{B,C}和{B,D},α的其他擴展是{B,C,D}。
定義11 負項的擴展項集[19]。項集α可以擴展到項集Y,其中Y=α∪{X},并且X是含負項的一組項。
基本原理α∪{X}僅以少于或等于包含項集α的事務數量發生。項集X包含正項項集,并且其擴展可能大于或等于或小于項集X的效用。項集X包含負項項集,并且其擴展必須小于項集X的效用。從上面的描述,可以得出結論,如果項集X的效用值不小于min_util,則將負項集添加到項集X。如果擴展項集X的效用值仍大于或等于min_util,則該項集為高效用項集。
2.2 剪枝策略
THN算法采用重新定義的本地效用和重新定義的子樹效用對搜索空間進行了有效的修剪,基于這兩種方法該算法的效率得到了有效地提升。
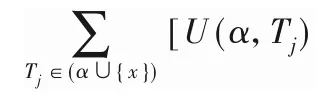
屬性3 基于重新定義本地效用的高估[19]。對于項集α和項x,其中x∈E(α)。令x可以是α的擴展,即x∈X。因此,RLU(α,x)≥U(X)始終成立。詳細證明見文獻[14]。
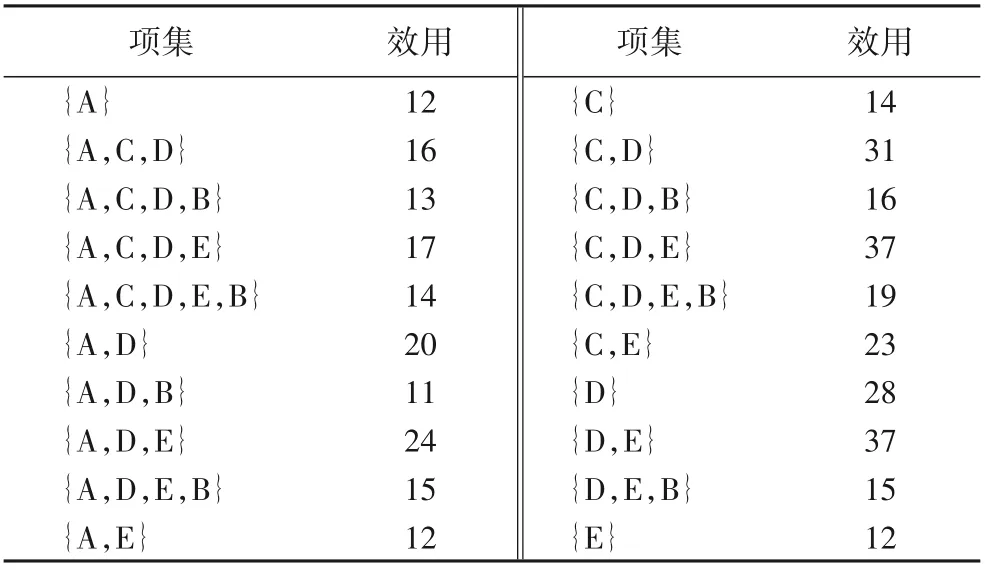
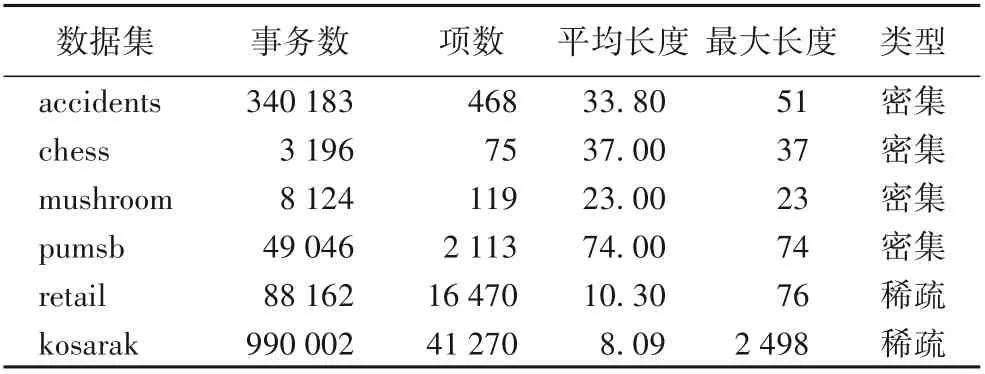
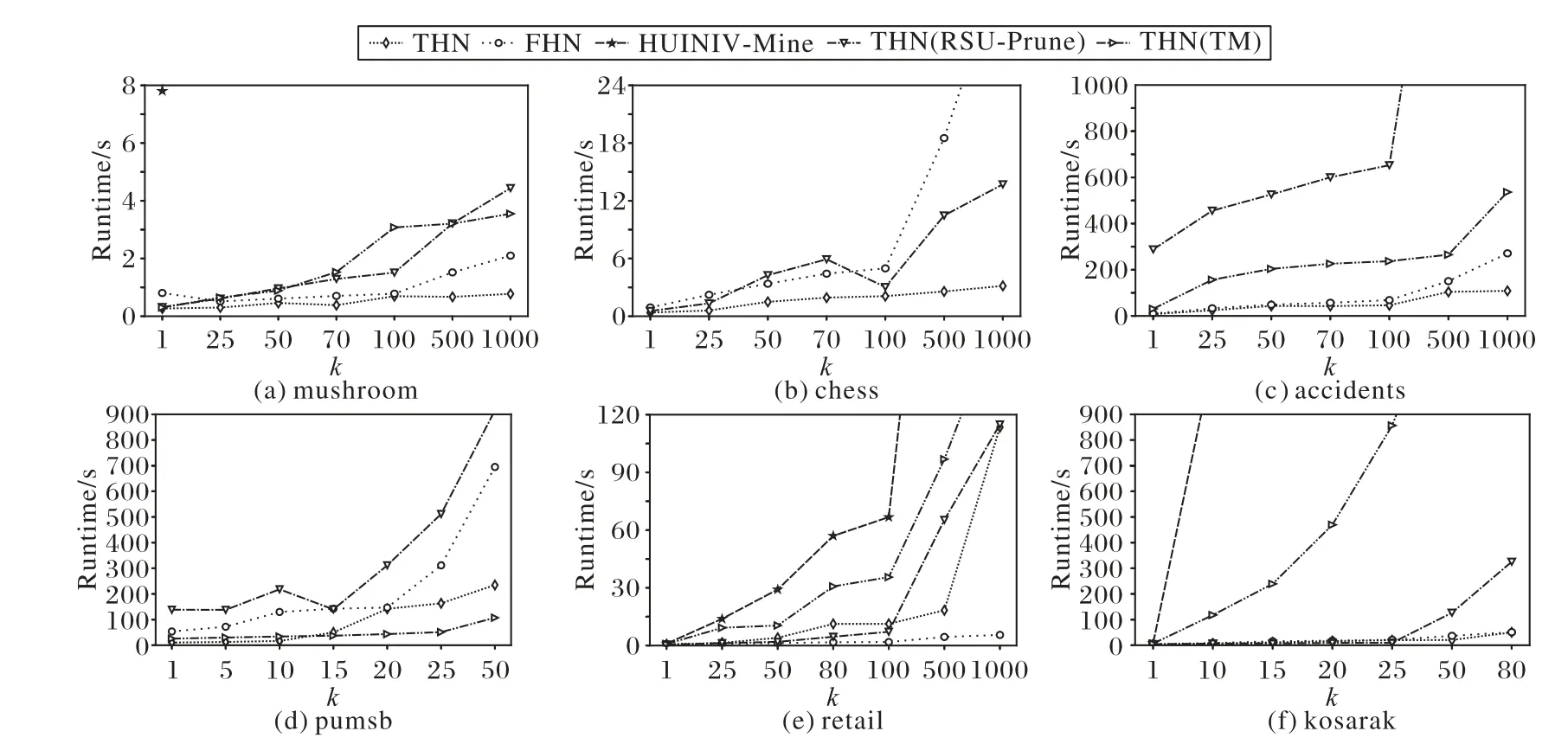
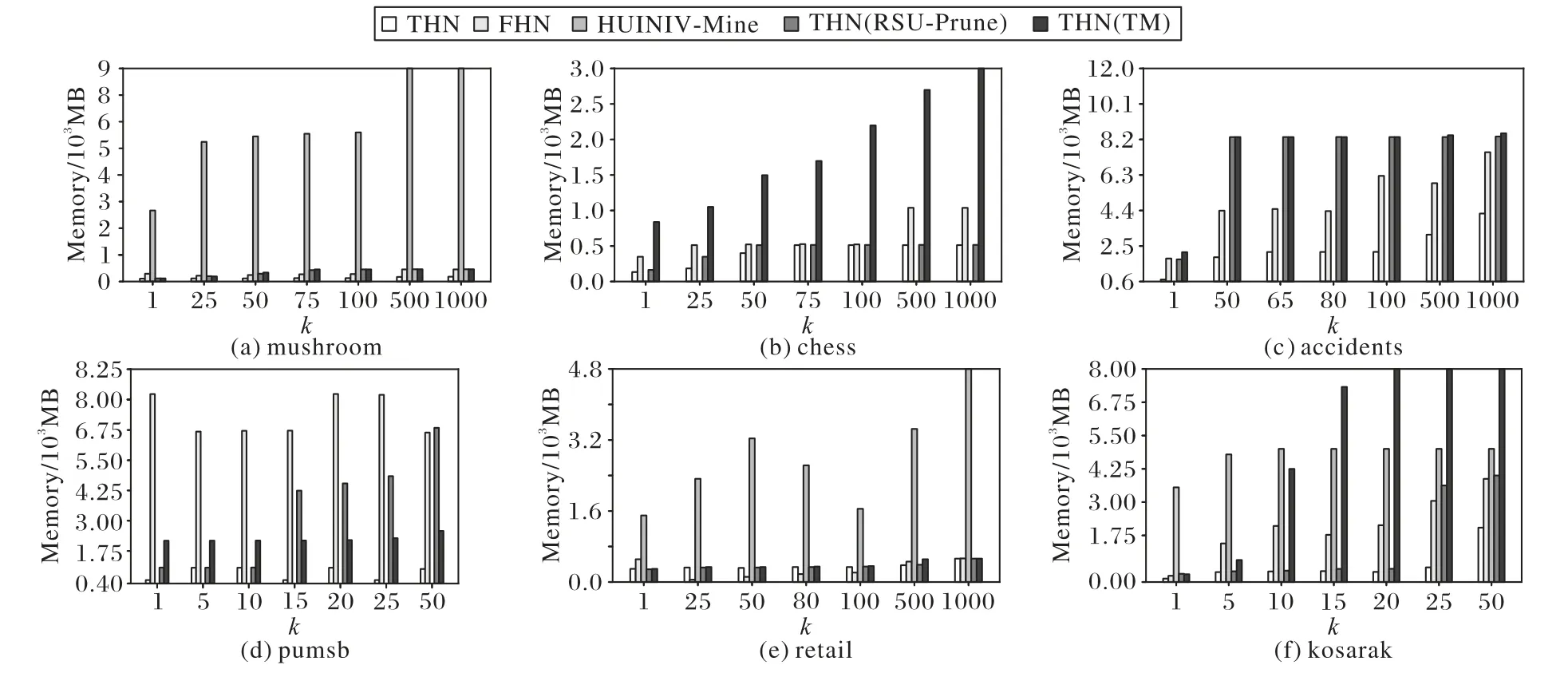
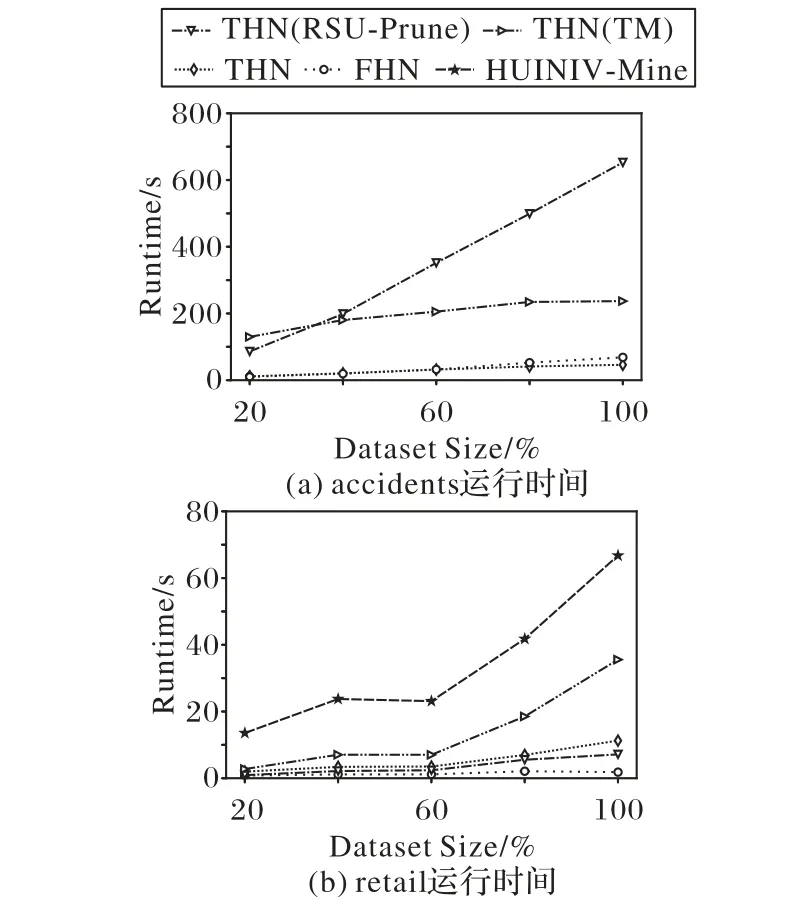
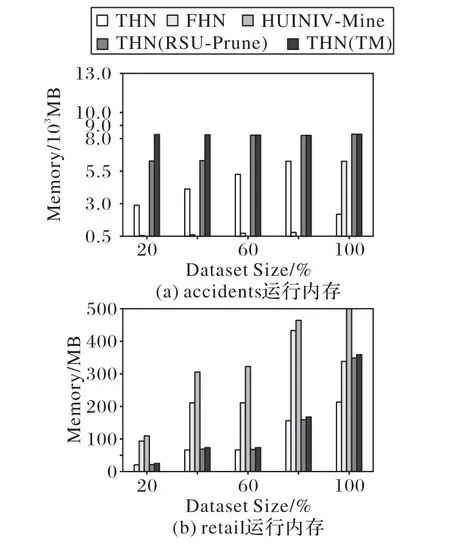
這是使用重新定義的本地效用修剪搜索空間的方法。對于項集α和項x,其中x∈E(α)。如果RLU(α,x) 屬性4 基于重新定義子樹效用的高估[19]。令項集α和項x,其中x∈E(α)。RSU(α,x)的效用值大于等于U(α∪{x}),則相應的取值。其中,RSU(α,x)≥U(x)保持α∪{x}的擴展X。 使用RSU修剪空間。設項集α和項x,其中x∈E(α)。如果RSU(α,x)小于min_util,則將項集擴展為單項(α∪{x}),并擴展低子樹效用值。此外,在集合枚舉樹中修剪α∪{x}的子樹,可以修剪項集α的子樹。 目前,高效用項集挖掘算法在挖掘高效用項集時通常使用剩余效用進行剪枝。在利用剩余效用進行剪枝的過程中,如果項集α帶有項x的效用小于min_util,則只刪除子節點。在利用重新定義的子樹效用進行剪枝的過程中,如果項集α帶有項x的效用小于min_util,則刪除子項集。因此,使用重新定義的子樹效用進行修剪時,將極大地提高算法的性能。 定義14 主要項和次要項[19]。對于項集α,項集α的主要項表示為Primary(α)={x|x∈E(α)∧RSU(α,x)≥min_util}。項 集α的 次 要 項 表 示 為Secondary(α)={x|x∈E(α)∧RLU(α,x)≥min_util}。其 中RLU(α,x)≥RSU(α,x),因此Primary(α)?Secondary(α)。 本章詳細介紹了THN算法,包括使用的事務合并和投影數據集技術、使用效用數組計算效用上界的方法、提出的閾值提升策略和THN算法的偽代碼。 該算法利用事務合并和數據集投影技術減小數據集的大小,從而降低了數據集的掃描成本。投影數據集只被掃描一次,以合并相同的事務。 表5 事務合并后的數據集Tab.5 Dataset after transaction merging 定義16 投影數據集[19]。對于項集α,投影數據集D表示為α-D,定義為α?D={α?T|T∈D∧α?T≠0}。 為了進一步壓縮數據集,本文算法需要合并投影數據集中的事務。投影事務合并比原始事務合并產生更高的數據集縮減量,因為投影事務比原始事務小,因此,投影事務更有可能是相同的。 表6 項C投影數據集Tab.6 Projected dataset of item C 表7 事務合并投影后的數據集Tab.7 Dataset after transaction merging projection 為了減小數據集的大小,需要使用事務合并技術。實現此技術的主要問題是識別相同的事務。為了實現這一點,本文算法需要相互比較所有的事務。將所有事務與每個事務進行比較的技術并不是一種有效的技術。為了解決這個問題,本文算法可以采用文獻[33]中提出的相同事務排序技術?T。這種排序技術在計算上并不昂貴。 定義18 事務的總順序[33]。在事務數據集D中,當向后讀取事務時,總順序?T被定義為字典順序。有關?T的更多闡述可以參考文獻[33]。 為了降低數據集掃描的成本,THN算法使用了事務合并和數據集投影技術。當數據集包含相同的事務時,事務合并技術識別這些相同的事務,并將其替換為單條事務。事務合并技術是減小數據集大小的理想方法。數據集投影技術使較長的事務變得較短,當搜索較長的項集時,投影數據集的大小也會減小,從而降低了數據集掃描成本。目前,FHN算法使用垂直數據集且沒有使用事務合并技術。 定義19 效用數組[19]。I是數據集D中出現的一組項,UA是一個長度為||I的數組,其中每個項x∈I都有一個表示為UA[x]的條目。每個條目稱為UA,用于存儲效用值。 1)用UA計算RLU(α)。 首先,UA初始化為0。其次,對于數據集D的每個事務Tj,所有項x∈Tj∩E(α)的UA[x]計算為UA[x]=UA[x]+U(α,T)+RU(α,T)。掃 描 數 據 集 后,UA[x]包 含RLU(α,k),?k∈E(α)。 2)用UA計算RSU(α)。 top-k高效用項集挖掘算法的主要問題局限是,沒有預先提供min_util,運行時的min_util從0或1開始,這嚴重降低了算法的效率。因此,這為如何自動提升min_util而不丟失任何高效用項集帶來了巨大的挑戰。為了解決這個問題,本文提出了有效的RTWU_strategy閾值提升策略。 RTWU_strategy閾值提升策略的詳細過程如下所述。首先,在第一次掃描事務數據集時,計算此過程中所有項的RTWU(x)。例如,項A同時出現在事務T1、T5和T6中。項A在事務T1、T5和T6中的RTWU為RTWU(A)=RTU(T1)+RTU(T5)+RTU(T6)=32。根據此方法,計算所有項的RTWU(x)。然后,令RTWU={RTWU1,RTWU2,…,RTWUn}為I中項的效用列表。接下來根據定義18中的排序規則,對RTWU效用列表進行排序。然后,RTWU_strategy將已排序的RTWU效用列表中的min_util提升到第k個最大值。現在,使用這個新值作為min_util。例如,假設用戶將k值設置為5,然后掃描數據集并計算項的RTWU(x)。假設效用列表中RTWU的第5個值是88,那么,min_util提高到88。然后,該算法使用這個新的min_util。最后,直至找到用戶需求的效用值最高的前k個項集,RTWU_strategy閾值提升策略的偽代碼如算法1所示。 算法1 RTWU_strategy。 輸入:所有項的RTWU集合,k:所需的高效用項集的數量; 輸出:提升min_util。 1)SortRTWUvalues; 2)Setmin_utilto thekthlargestRTWUvalue; 3)returnmin_util. 本文提出的THN算法利用了前面介紹的幾種策略。算法2為主算法,將事務數據集D和用戶定義的高效用項集的數量k作為輸入,輸出是top-k高效用項集。 第1)至4)行分別表示初始化α為空項集,ρ表示一組正項集,η表示一組負項集,將min_util初始化為1。第5)行創建創建一個k大小的優先隊列(名為k_Patterns)。第6)行掃描事務數據集D,同時使用UA技術計算所有項的RLU。第7)行通過比較每個項的RLU和min_util,可以獲得項集的次要項,次要項作為項集的擴展項。第8)行計算每個項的RTWU,并將結果存儲在hashMap中。第9)行調用RTWU_strategy,主要功能是自動提升min_util。第10)行根據RTWU的升序對項集進行排序。注意,當按?T順序排序時,該算法首先考慮正效用項,然后考慮負效用項。第11)行掃描數據集D,并刪除事務中不是次要項的所有項集和空事務。根據重新定義的本地效用的剪枝策略,刪除的項不是高效用項集。第12)行根據字典排序對剩余事務進行排序,且正項集在負項集之前。此時,根 據EFIM(efficient algorithm for high-utility itemset mining)[33]的建議,此處執行事務合并技術。第13)行掃描數據集D,并使用UA技術計算所有項的RSU。第14)行通過比較每個項的RSU和min_util,可以獲得項集的主要項。第15)行通過調用算法3從項集α開始遞歸執行深度優先搜索。THN算法的偽代碼算法2所示。 算法2 THN算法。 輸入:事務數據集D,潛在高效用項集的數量k; 輸出:top-k高效用項集。 1)α←?; 2)ρ←set of positiveutility items inD; 3)η←set of negativeutility items inD; 4)min_util←1; 5)Createa priority queuek_Patternsof sizek; 6)Scan datasetD,computeRLU(α,X)for all itemsX∈ρ,usingUA[X]; 7)Secondary(α)={X|X∈ρ∧RLU(α,X)≥min_util}; 8)ComputeRTWU(X)for all itemsk∈Iand store theseRTWUvalues them in a hashMap; 9)RTWU_strategy(hashMapRTWU,k); 10)Let?Tbe the total order ofRTWUincreasing values onSecondary(α); 11)ScanD,remove itemx?Secondary(α)from the transactionsTjand delete empty transactions; 12)Sort all the remaining transactions in the datasetDaccording to?Twith positive utility items followed by negative utility items; 13)ScanD,compute theRSU(α,X)of each itemx∈Secondary(α),usingUA[x]; 14)Primary(α)={X|X∈Secondary(α)∧RSU(α,X)≥min_util}; 15)Search_P(η,α,D,Primary(α),Secondary(α),min_util,k_Patterns); 16)return top-kHUIs. 算法3的輸入如下:η表示一組負項集,α為項集,α-D代表投影數據集,Primary(α)代表項集α的主要項,Secondary(α)代表項集α的次要項,min_util表示最小效用閾值,k_Patterns表示為k個項的優先級隊列;輸出為前k個α項集擴展的含正項高效用項集集合。 算法3第1)~2)行只能找到具有正項的擴展,每次都遞歸地調用自己用主要項來擴展每個次要項α。單項集的擴展技術遵循定義11。第3)行掃描數據集α-D,計算每個擴展項集β的效用,然后構造新的投影數據集β-D。在這個過程中,執行事務合并與投影數據集技術。第4)行項集β的效用值不小于min_util,然后把它添加到優先級隊列k模式中。同時,將該min_util提升到優先級隊列元素min_util的頂部。第6)行當項集β的效用值大于min_util,則調用算法4用負項來擴展該項集;否則,第8)行掃描投影數據集β-D,并使用UA技術計算每個項的RSU和RLU。第9~10)行找到項集β的主要和次要項。第11)~12)行算法3利用深度優先搜索的方法反復執行用主項對項集β的擴展,一直執行到滿足條件為止,Search_P算法的偽代碼如算法3所示。 算法3 Search_P算法。 輸入:一組負項η,項集α,投影數據集α-D,α的主要項Primary(α),α的次要項Secondary(α),最小效用閾值min_util,k個項的優先級隊列k_Patterns; 輸出:前k個α項集擴展的含正項高效用項集集合。 1)for each itemx∈Primary(α)do; 2)β=α∪{x}; 3)Scanα-D,computeU(β),and createβ-D; 4)ifU(β)≥min_utilthen addβink_Patterns.And raise themin_utilto the top of priority queueelement’sutility; 5)end if 6)ifU(β)>min_utilthen search_N(η,β,β-D,min_util,k_Patterns); 7)end if 8)Scanβ-D,computeRSU(β,x)andRLU(β,x)where itemx∈Secondary(α),using twoUAs; 9)Primary(β)={x∈Secondary(α)|RSU(β,x)≥min_util}; 10)Secondary(β)={x∈Secondary(α)|RLU(β,x)≥min_util}; 11)search_P(η,β,β-D,Primary(β),Secondary(β),min_util,kPattens); 12)end for. 算法4的輸入如下:η表示一組負項集,α為項集,α-D是投影數據集,min_util表示最小效用閾值,k_Patterns:表示k個項的優先級隊列;輸出為前k個α項集擴展的含負項高效用項集集合。 當項集β的效用值大于min_util時,算法4的調用條件才存在。第2)行該算法是使用負項進行擴展的。它使用定義11對所需項集負擴展的搜索空間進行修剪。第3)行掃描數據集α-D,計算每個擴展項集β的效用,然后構造新的投影數據集β-D。在這個過程中,執行事務合并與投影數據集技術。第4)行項集β的效用值不小于min_util,然后把它添加到優先級隊列k模式中。同時,將該min_util提升到優先級隊列元素min_util的頂部。第6)行掃描投影數據集β-D,并使用含負項UA技術計算每個項的RSU。第7)行找到項集β的主要項。第8)~9)行該算法將遞歸調用自身,用負項對項集β進行擴展,一直執行到滿足條件為止,Search_N算法的偽代碼如算法4所示。 算法4 Search_N算法。 輸入:一組負項η,項集α,投影數據集α-D,最小效用閾值min_util,k個項的優先級隊列k_Patterns; 輸出:前k個α項集擴展的含負項高效用項集集合。 1)for each itemx∈ηdo; 2)β=α∪{x}; 3)Scanα-D,computeU(β),and createβ-D; 4)ifU(β)≥min_utilthen addβink_Patterns.And raise themin_utilto the top of priority queue element’s utility; 5)end if 6)CalculateRSU(β,x)for all itemx∈ηby scanningβ-Donce,using thenegativeUA; 7)Primary(β)={x∈η|RSU(β,x)≥min_util}; 8)search_N(β,β-D,Primary(β),min_util,k_Patterns); 9)end for. 在本節中,給出一個簡單的說明性示例,以展示THN算法如何從事務數據集中找到含負項top-k高效用項集。假設如表1所示的7條事務,并且有5個項的內部效用。同時,表2顯示每個項的外部效用。此外,最終挖掘出的效用值最高項集的數量k被設置為20。THN算法從事務性數據集中挖掘高效用項集,THN算法首先計算事務中每一項的效用,并找到該事務的事務效用。例如,事務T2中有3個項B、C和E,它們的內部效用值分別是1、5和1。表2中的B、C和E的外部效用分別為-3、1和1。那么T2中B、C和E的效用值可以分別計算為1*(-3)=(-3),5*1=5和1*1=1。經過上述過程,可以計算出T2的TU為(-3)+5+1=3。所有事務的TU值結果如表3所示。為了過高估計效用,THN算法使用RTU。為了找到RTU,THN算法只計算正效用值為5+1,即在T2中為6。同樣,所有RTU都可以計算出來。所有事務的RTU如表4所示。RLU是使用深度優先搜索計算的。運行示例中項A的RTWU值出現在三個事務T1、T5和T6中,它們的RTU值分別為11、4和17。因此,項A的RTWU可計算為11+4+17=32。根據項的RLU不小于min_util,然后找到次要項集。Secondary={A,B,C,D,E}。在這之后,所有的項都按照RTWU升序排序,負項總是在正的項集之后。 然后,不屬于次要項集的項被刪除。因此,沒有從示例數據集中刪除任何項。同時,如果從事務中刪除了所有項,則刪除那些空事務。然后對剩余的事務按總順序?T進行排序。之后,本文提出的THN算法再次掃描數據集,計算所有項集的RSU。RSU不小于min_util的項位于主要項中。因此,Primary={A,C,D,E},只使用主要項集的項進行深度優先搜索。所有次要項集{A,C,D,E,B}的項作為每個子樹的子代節點。為此,使用深度優先搜索來查找子樹中的下行節點。使用算法2和算法3對節點進行挖掘,然后遞歸地調用算法2來擴展所有具有正項,然后調用算法3擴展具有負項。在運行的示例中,假設k值為20,最終的top-k高效用項集如表8所示。運行示例的高效用項集是{{A}:12,{C}:14,{A,C,D}:16,{C,D}:31,{A,C,D,B}:13,{C,D,B}:16,{A,C,D,E}:17,{C,D,E}:37,{A,C,D,E,B}:14,{C,D,E,B}:19,{A,D}:20,{C,E}:23,{A,D,B}:11,{D}:28,{A,D,E}:24,{D,E}:37,{A,D,E,B}:15,{D,E,B}:15,{A,E}:12,{E}:12},其中每個項集旁邊的數字表示其效用值。 表8 top-k高效用項集Tab.8 top-k high utility itemsets 為了測試THN算法的性能,本文做了大量的實驗。通過擴展spm f[34]上的開源Java庫,可以實現該實驗。該實驗運行環境的CPU為3.00 GHz,內存為256 GB,操作平臺是Windows 10企業版。該實驗使用了六個真實的數據集mushroom、chess、accidents、pumsb、retail和kosarak,所有數據集都是從spm f上下載的。表9顯示了數據集的基本特征,每一列從左到右分別表示數據集名稱、事務數量、項的個數和數據集密度。 表9 數據集的基本特征Tab.9 Basic characteristicsof datasets 對于所有的數據集,項的內部效用值在1~5的范圍內隨機生成,項的外部效用值使用對數正態分布在-1 000~10 000生成。為確保結果的穩健性,本文所有的實驗都進行了10次,并統計了平均結果。 本文為了評估所提出的技術在THN中的影響,因此檢驗了THN(RSU-Prune)和THN(TM)的性能。THN算法同時利用了數據集合并技術TM和剪枝策略RSU。THN(RSU-Prune)僅在TM被禁用的情況下使用修剪策略RSU。類似地,THN(TM)僅使用數據集合并技術TM,其中剪枝策略RSU是禁用這種變化。本文提出的THN算法是第一個挖掘含負項top-k高效用項集挖掘算法。因此,找不到具有相同性能的另一算法進行比較。 傳統上,測試新正項的top-k高效用項集挖掘算法是將其與挖掘相同結果集并設置最佳最小效用閾值的非top-k高效用項集挖掘算法進行比較。對于新提出的THN算法,本文通過查找相關文獻得出,FHN算法[11]是挖掘含負項最先進的高效用項集挖掘方法。HUINIV-Mine[9]算法也是產生負效用的高效用項集挖掘算法,但是HUINIV-Mine的執行時間在有的數據集中無法在圖中畫出來,因為它需要更多的執行時間和內存。因此,對比非top-k算法是HUINIV-Mine和FHN算法,這兩種算法均被用于挖掘含負項高效用項集。 為了確保挖掘出相同的結果集,本文為HUINIV-Mine和FHN算法選擇了最佳min_util。這樣,可以以相同數量相同結果集的模式進行性能比較。為了評估性能,本文通過提高k值來執行所有數據集上的所有變化,直到所有的變化花費太多的時間或內存不足。 本節評估了THN算法和對比算法在所有數據集中的運行時間性能。圖1顯示了THN算法和對比算法在所有數據集的運行時間情況。從圖1中可以清楚地看到,在mushroom、chess、accidents和pumsb密集數據集中,THN算法的運行時間遠少于HUINIV-Mine、FHN算法。因為HUINIV-Mine在chess和accidents數據集中,即使k值設置為1,也需要耗費長達數小時的執行時間,因此在圖1中沒有畫出。在mushroom和pumsb數據集中,當k的值設置得較大時,THN算法與HUINIV-Mine、FHN算法之間的運行時間間隔變大。在mushroom、chess、accidents和pumsb數據集中k的值小于100時,THN算法和FHN算法的運行時間沒有太大差異。當k值超過500時,mushroom、chess、accidents和pumsb數據集在FHN算法中的運行時間會激增,而THN算法的運行時間則相對穩定。從圖5中可以看出,數據集掃描技術和基于重新定義子樹效用的剪枝技術相結合在密集數據集中得到了很好的使用。但是在mushroom、chess、accidents數據集中THN(TM)和THN(RSUPrune)總是比THN算法執行時間長,但是在pumsb數據集中THN(TM)比THN算法執行更少的時間。這種現象表明,事務合并對于具有大量不同項和項的平均長度較大的數據集執行得很好。從密集數據集中可以看出,當k值設置較高時,本文算法與FHN之間的差距較大,說明本文算法比FHN運行的k值更高。FHN的性能不好的主要原因是,它加入了較小項集的效用列表,以生成較大的項集。FHN考慮沒有出現在數據集中的項集,因為它們通過合并較小的項集來探索項集的搜索空間,而不掃描數據集。由于密集的數據集包含大量的長項和事務,因此提出的THN算法性能更好。 從圖1中可以清楚地看到,在retail和kosarak稀疏數據集中,FHN算法的運行時間少于HUINIV-Mine和THN算法。在retail數據集中,隨著k值的增加,FHN算法的運行時間幾乎不變。在retail數據集中當k的值小于500時,在kosarak數據集中當k的值小于50時,THN算法的運行時間和FHN算法的運行時間幾乎持平。在retail數據集中,THN(RSU-Prune)算法的執行時間小于THN算法。這一結果表明,retail數據集不支持TM技術。Retail數據集有大量不同的項,并且比所有其他數據集有更寬的最大長度,因此它不支持TM技術。實驗結果表明,在數據集高度稀疏的情況下,THN算法可以放棄TM技術,有效地挖掘高效用項集。因此,在retail和kosarak稀疏數據集中,THN(TM)算法的性能遠低于FHN算法。因為稀疏數據集,它們具有大量不同的項,幾乎沒有相同事務。由于在稀疏數據集中,事務數據庫中具有相同項的事務的概率顯著降低,所以事務合并策略變得開銷很大。THN算法提出的事務合并技術在高度稀疏的數據集中表現不佳,事務合并需要大量時間來合并事務,稀疏數據集中的相同事務較少,因此浪費大量時間,效率很低。 圖1 不同算法的運行時間對比Fig.1 Comparison of runtimeof different algorithms 本節評估了THN算法與對比算法在所有數據集中的內存消耗的性能。圖2顯示了THN算法和對比算法在所有數據集的運行時間情況。 從圖2中可以清楚地看到,在所有密集數據集mushroom、chess、accidents和pumsb中,THN算法的內存消耗值遠低于HUINIV-Mine和FHN算法。在chess、accidents和pumsb密集數據集中,THN(TM)和THN(RSU-Prune)的內存消耗遠比HUINIV-Mine和FHN算法小。隨著k值的增加,FHN的內存消耗迅速增加。對于mushroom密集數據集,THN算法的內存消耗遠小于HUINIV-Mine和FHN算法。但是,THN(TM)和THN(RSU-Prune)算法的內存消耗大于FHN算法。在chess和accidents數據集中,隨著k值的增加,THN算法消耗的內存幾乎保持不變,而FHN算法消耗的內存是THN算法消耗的內存的三倍。對于所有密集數據集,在THN算法中,TM技術和RSU技術可以更好地結合在一起。因此,THN算法比其他算法使用更少的內存。HUINIV-Mine和THN算法在大多數情況下都需要高內存,其中,因為FHN算法將所有的效用列表保存在內存中以進行連接,因此需要消耗大量的內存空間。 從圖2可以清楚地看到,在稀疏數據集kosarsk中,THN算法的內存消耗遠遠小于HUINIV-Mine和THN算法。THN(RSU-Prune)算法的內存消耗也小于HUINIV-Mine和THN算法,可以看出RSU的剪枝策略在THN算法中得到很好的使用。但是,THN(TM)算法的內存消耗大于THN算法,可以得出在稀疏數據集kosarsk中,TM技術并不能提高內存消耗的性能。在retail數據集中,THN的內存消耗遠小于HUINIV-Mine算法。但是,在k值小于500時,THN算法及其THN(TM)和THN(RSU-Prune)算法的內存消耗比FHN多。因為,retail數據集是高度稀疏的,所提出的算法對高度稀疏數據集不是有效的。THN采用的TM技術不適用于retail等高度稀疏的數據集。 圖2 不同算法的內存消耗對比Fig.2 Comparison of memory usageof different algorithms 本節從算法的可擴展性角度對所有算法進行了實驗。該實驗選取了密集數據集accidents和稀疏數據集retail,實驗數據大小20%~100%不等,k值設置為100。通過以上設置,可以更好地展示所有算法的可伸縮性。圖3顯示了THN算法的運行時間隨著數據集大小的增加而線性增加。圖4顯示了THN算法隨著數據集大小的增加內存消耗也線性增加,但在FHN算法中,內存消耗則急劇增加。以上實驗結果表明,THN算法在不同數據集和參數下都具有可擴展性。 圖3 不同算法運行時間的可擴展性Fig.3 Scalability of runtimeof different algorithms 圖4 不同算法內存消耗的可擴展性Fig.4 Scalability of memory usageof different algorithms THN算法是挖掘含負項top-k高效用項集挖掘算法,使用基于RSU搜索空間的剪枝策略,為了減少數據集的掃描次數,使用了事務合并和數據投影相結合的技術。該算法在四個密集數據集和兩個稀疏數據集上進行了實驗。對比算法使用了本身的變形算法THN(TM)和THN(RSU-Prune),還有挖掘含有負項高效用項集挖掘算法HUINIV-Mine[9]和FHN[11]。 由于在實驗中為HUINIV-Mine和FHN算法設置min_util,這對于THN算法是不公平的,因為top-k高效用項集挖掘問題總是比相應的非top-k高效用項集問題更困難。主要原因是非top-k高效用項集挖掘算法直接設置了最佳min_util,top-k高效用項集挖掘算法min_util開始為0,然后逐漸增加min_util直到找到k個項集。非top-k高效用項集挖掘算法將在此過程中減少很大一部分搜索空間。在本實驗中,本文直接為HUINIV-Mine和FHN算法設置了最佳min_util,這使得該算法具有很大的優勢。對于每個不同的數據集,在運行THN算法時會設置不同的k值。在不同的數據集上運行HUINIV-Mine和FHN算法之前,將min_util設置為HUINIVMine和FHN算法以挖掘k個項集中的最小效用值。 從實驗結果可以看出,THN算法在mushroom、chess、accidents、pumsb和kosarak數據集的運行時間效率上有了顯著提高,在retail數據集上的執行時間是可比較的。HUINIVMine算法在accidents、chess、pumsb和kosarak數據集中,因為需要太長的執行時間和內存消耗而崩潰。因此,運行時間和內存消耗沒有顯示。此外,THN在所有數據集上的內存改進是相當顯著的。與HUINIV-Mine和FHN算法相比,THN在除retail外的所有數據集上的運行時間效率和內存消耗性能都有顯著提高。 本文提出含負項top-k高效用項集挖掘算法——THN。當用戶挖掘含負項高效用項集時,可以直接設置所需的項集數k,而無需反復調整min_util挖掘用戶需求高效用項集的個數。THN算法是一階段高效用項集挖掘方法,該算法使用深度優先進行搜索。為了減少數據集的掃描次數,該算法使用事務合并技術和數據集投影技術。為了更好地修剪搜索空間,該算法使用了基于重新定義的子樹修剪策略。為了提高算法的性能,該算法提出了自我提升最小效用閾值的策略。實驗結果表明,THN算法的性能明顯優于對比算法,并且該算法在密集數據集中的表現尤其出色。但是,該算法在稀疏數據集的運行時間上效果較差。盡管THN算法在稀疏數據集上運行需要更長的時間,但其仍然是第一個挖掘含負項top-k高效用項集挖掘算法。最后,本文還對THN算法進行了可擴展性測試,結果表明該算法具有良好的可擴展性。 由于該算法在稀疏數據集上的表現不佳,未來的工作可以研究如何降低該算法在稀疏數據集上運行的時間。目前,含負項高效用項集挖掘算法較少,在下一步的工作中,我們可以研究在增量數據集和大數據中挖掘含負項高效用項集和挖掘精簡的含負項高效用項集。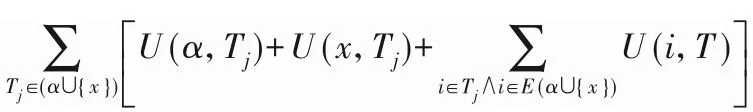
3 THN算法
3.1 數據集掃描技術
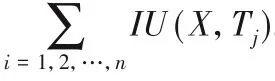

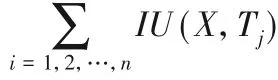


3.2 效用數組結構
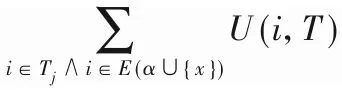
3.3 閾值提升策略
3.4 THN算法描述
3.5 THN算法示例
4 實驗與結果分析
4.1 實驗設計
4.2 執行時間性能
4.3 內存消耗性能
4.4 可擴展性
4.5 實驗結論
5 結語

