聚焦核心概念，讓方法的教學“有根”

于萍 劉克臣

【摘 要】“分數和小數的互化”一課通常不是教師心目中的“大課”，一方面它不屬于概念的起始課，另一方面從掌握方法的角度看其內涵并不復雜。甚至在有的版本教材中并沒有安排特定的例題，而是“藏”在練習中一帶而過。本文通過“課前思考”系統分析了這節課的內容價值，在“課中實踐”部分，翔實反映實施效果，最后以“課后評析”促實踐者再思考，呈現了一個“聚焦核心概念進行方法教學”案例研究的全過程。

【關鍵詞】核心概念 溝通聯系 數學素養

一、課前思考

思考一：上一節“技能課”還是“概念課”？

立足單元整體目標分析，本課的教學重點不應僅是探索分數和小數互化的方法，讓學生掌握技能，更要對“分數和小數為什么互化”“互化背后的本質是什么”等問題進行深入探究，讓本課從單純的“技能課”轉向“概念課”，更好地聚焦核心概念，讓方法的教學因深刻而靈動。

思考二：除了掌握方法，還有哪些價值？

突出用聯系的眼光看問題——理解“同”。小數的本質是十進分數，因此和分數有著密切的聯系。“小數的初步認識”及“小數的意義”的教學內容都是借助分數認識小數。此后，因其十進計數的特征，使得小數的運算與整數運算方法一脈相承，而分數的運算方法則與其有顯著差異。形象地說，初識小數時，它和分數的關系十分緊密;在此后較長時間的學習中，二者卻相對獨立;在“分數和小數的互化”一課中它們再一次“密切接觸”。應讓學生把握分數和小數相同的本質，進而理解各自運算方法的相通。通過互化，讓分數和小數可在彼此的世界里“暢通無阻”，實現運算方法、運算定律的有效推廣。

突出用對比的方法想問題——感受“異”。我們要幫助學生感受分數和小數各有各的特點和價值，這種獨特性表現為：分數具有簡潔而精準的應用特點，但由于它的分數單位可以是任意的，因此其大小不容易被感知。而小數具有應用廣泛和近似的特點，且采用十進位值制計數法，其大小更容易被感知。此外，分數除了可以表示具體數量，還能夠清晰、簡潔地表達兩個量之間的關系。

二、課中實踐

（一）問題引入

1.提問

師：這節課我們來研究“分數和小數的互化”（板書課題），你理解“互化”這個詞的意思嗎？

生：就是互相轉化的意思。

師：你有什么問題或想法嗎？

生1：分數和小數能不能轉化？

生2：分數和小數怎么互化？

生3：分數和小數為什么要互化？什么情況下互化？

2.追問

師：既然是“互化”，你能試著將第一個問題問得更具體些嗎？

生：分數怎樣轉化為小數？小數怎樣轉化成分數？

師：很多時候，我們思考問題、研究問題，就是要通過這樣的追問，讓問題變得更具體、更清晰。

師（小結）：前兩個問題提得很好，第三個問題提得更好。一說學習“分數和小數的互化”，大家比較容易想到“怎么互化”這種指向方法的問題，但能夠想到“為什么要互化”的同學，思考得更深刻。好問題往往是好研究的開始。這節課我們就圍繞同學們提出的這些問題展開討論。

設計意圖：學起于思，思起于疑。用課題引導學生主動思考“學什么”和“為什么學”，這兩個問題分別指向方法和價值。教師要抓住機會培養學生的問題意識。

（二）探究方法

1.算一算，感受聯系

師：有一根3m長的絲線，如果將它平均分成4份，每份有多長呢？試著列式解決這個問題。

（生列式并匯報計算結果，根據除法與分數的關系可以得到分數結果;根據小數除法的計算方法也可以算出小數結果）

[板書：3÷4=0.75（m），3÷4=3/4（m）]

師：同一個除法算式，計算的結果既可以是個小數，還可以是個分數。你能得出什么合理的推論嗎？

生（異口同聲）：0.75=3/4或3/4=0.75。

師（小結）：看來小數和分數之間的確有密切的聯系，只有在相等的情況下才能夠相互轉化。

設計意圖：調動已有的認知經驗，通過推理發現分數和小數的聯系，明確“轉化”的前提是“相等”。

2.想一想，探尋方法

嘗試解決下面的問題：

（1）活動要求：先獨立完成，再小組4人交流研究成果，最后提出問題或總結方法。

（2）作品反饋：

方法一：

師：你能看懂這名同學的方法嗎？這個方法的價值是什么？

生：將分數和小數比較的問題轉化成了整數間的比較，這個方法很好。

方法二：

師：這種方法你能看懂嗎？這樣做的道理是什么？

生：將分數化成小數，再比較兩個小數的大小。

師：他是如何將分數轉化成小數的？

生：用分子除以分母。

（師板書分數轉化小數的方法）

方法三：

師：這種做法你能看懂嗎？這樣做的道理又是什么？

生：將小數化成分數，再比大小。

師：你認為在這個方法中哪個數的出現很關鍵？

生（異口同聲）：4 /5 。

師：怎么就想到這個分數了呢？

生：一位小數就是十分之幾，兩位小數就是百分之幾……所以0.8就是4/5 。

師：你能試著概括一下將小數轉化成分數的方法嗎？

生：先根據小數部分的位數，直接寫成十分之幾、百分之幾、千分之幾……的分數，再化簡。

師（小結）：我們對小數很熟悉，豐富的經驗讓我們把一位小數和十分之幾、兩位小數和百分之幾、三位小數和千分之幾……之間建立起緊密的聯系。現在，這些經驗幫助我們解決了新的問題，看來找到分數和小數之間的聯系是進行相互轉化的關鍵。

設計意圖：在解決問題過程中，學生充分調動已有的認知經驗，將新問題轉化為舊問題。方法雖不相同，但都是先統一形式再進行比較。學生通過調動已有認知經驗，探索出了分數和小數互化的方法。

3.練一練，鞏固方法

師：經過剛才的交流，大家對分數和小數之間的互化方法有所了解。接下來，請按要求做一做下面兩道練習題，并分別說說方法，看看你有什么新發現或新問題。

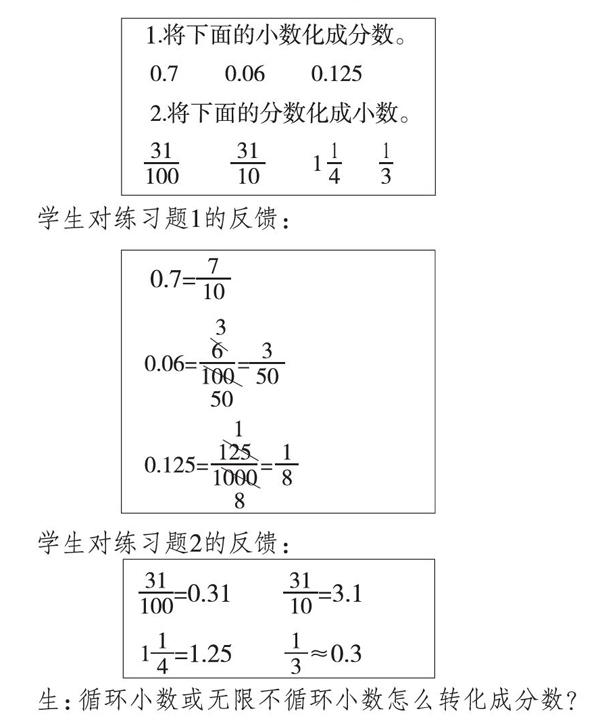
1.將下面的小數化成分數。

0.70.060.125

2.將下面的分數化成小數。

31 —100 ?31 —10 11 —4 ?1 —3

學生對練習題1的反饋：

0.7=7 —10

0.06=6 —100 =3 —50

0.125=125 —1000 =1 —8

學生對練習題2的反饋：

31 —100=0.31 ? ? ? 31 —10 =3.1

11 —4 ?=1.251 ?—3 ?≈0.3

生：循環小數或無限不循環小數怎么轉化成分數？

師：這個問題非常有價值。我們要有全面思考的意識，既然要探討分數和小數的互化方法，就要將小數的各種類型都考慮到，不能只想到常見的小數類型。關于這類小數如何轉化成分數，誰能說說自己的猜測？

生：我猜想可以一位一位地轉化，最后統起來。

師：你的想法很有道理，化整為零，逐位突破也許是種有效的方法。看來大家對“無限”的情況都很好奇，就像浩瀚無垠的星空，因為“看不到邊，望不到頭”，所以總是深深地吸引著人們不斷地去發現。數學的無限有很多，也同樣吸引著我們去研究。一節課中，我們難以解決所有的問題。但這類情況卻可以引發我們深入思考。剛才總結的方法為什么不能轉化無限小數呢？難在了哪兒？

生：因為無限小數的小數部分有無數位，無法確定分數的分母，也就是無法確定分數單位。

師：可見，在將小數轉化成分數的時候，最關鍵的是什么？

生（齊）：確定計數單位。

師：你們真是善于透過現象看本質。你們認為分數和小數之間的互化，“化”的是什么？

生：轉化的就是計（分）數單位。

師（小結）：同學們緊緊抓住了小數與分數的聯系、分數與除法的聯系，找到了二者相互轉化的方法，還理解了方法背后的道理。

設計意圖：練習中涉及各種類型的分數和小數，既鞏固基本方法，也促進學生主動思考。每個數的轉化都離不開計數單位，這種認識在無限小數面前被“放大”，學生自然而然地想到“怎么將無限小數轉化為分數”。面對這個問題，理解“為什么”比習得“怎么做”更有價值，教師通過“難在了哪兒”的追問，促進學生理解數概念的本質。

（三）感受價值

師：大家通過努力找到了分數和小數互化的方法，你們就像是分數和小數的翻譯家。從此，分數在小數的世界里可以“加減乘除”，小數也可以在分數的世界中“暢通無阻”了。你們想過嗎，什么時候該互化呢？

生：不是總要互化的，只在需要的時候才互化。

師：這里有兩條信息，請你按下面要求做。

生：“信息一”中，1 27/50米轉化成小數是1.54米。將身高轉化成小數后，更清楚，光看分數都不知道亮亮到底有多高，變成小數就更有感覺了。

師：就是因為小數的計數單位都是十分之幾、百分之幾、千分之幾……這樣有規律的，所以我們才會對小數有種“很熟悉”“很清楚”的感覺。那么，分數的單位是怎樣的呢？

生1：是各種各樣的，任何非0整數都可以作分母。

生2：“信息二”中的分數不需要化成小數，因為生活中沒有聽說過“0.125決賽”“0.25決賽”或“0.5決賽”，太別扭了。

生3：化成小數后也聽不出有多少人參加比賽、勝出多少了。

師：看來分數也有自己的優勢，它不僅能表示數量，還能清晰地表達量與量之間的關系。

設計意圖：結合生活，學生在閱讀中理解數據的含義，互化后再進行對比，感受分數與小數各自的特點，以此深化對數特征的理解。

三、課后評析

隨著學生一起經歷了心潮澎湃的課堂學習全過程后，內心迸發出一種驚喜：枯木逢春。為何有這樣的感受呢？

課也是有生命的，用心思考、精心設計、巧妙實施，課堂就會煥發出生機。一節大家公認“已經沒有研究價值”的“死課”被于老師重新設計、精彩演繹，重新煥發了生命力。

（一）“枯”于技能

技能作為一種程序性知識，熟練程度更多依靠訓練量的多少。多少年來，“分數與小數的互化”一課被視為一種技能課，學生只需掌握轉化的方法即可，應用也多局限于數學內部的比較、分數和小數的混合運算等。因此，教師對于此內容的教學更多的是采取強化訓練，目的是使學生熟練掌握轉化的方法。

（二）“發”于概念

概念相對于技能的內涵更加豐富，概念需要建立、理解、運用，需要從內涵和外延的角度全方位建立概念系統。就像于老師在“課前思考”中提到的，小數和分數通過互化，可以在彼此的世界里“暢通無阻”。這樣的思考將教學的重點引向對分數和小數的本質的關注，看似是在研究方法，本質是在促進學生對兩種數的深刻理解和認識。此時，互化變成打通兩數世界的橋梁。

（三）“長”于價值

學生有時 “十分可愛”，那就是教師講什么就聽什么、讓做什么就做什么。他們內心真的滿足了嗎？未必！關于分數和小數的互化，他們的內心始終有這樣一個疑問：分數和小數的互化就是為了比較大小和計算嗎？不光學生有這樣的疑問，教師內心深處也會有這樣的疑問存在。于老師關注到了、想到了，關鍵是努力解決了。課結尾的活動，真正讓學生感受到分數和小數互化的價值。課到此，眼前猶如看到了一棵樹的根不斷扎向泥土深處，正在發芽、結果，這不就是我們想要的課堂嗎？

枯木逢春，希望有越來越多的課煥發出青春，讓學生在茂密的數學森林中漫步、尋根、賞花、摘果！