水錘防護措施及計算分析
苑司樂
(鄭州大學綜合設計研究院有限公司,河南 鄭州 450002)
1 概述
隨著中國經濟社會的發展和物質生活水平的提升,原有的農田灌溉設施已經無法滿足當今節水型社會的需求。為響應國家節約型社會建設的要求,近些年各地根據自身實際進行了大量的農田灌溉設施的更新和改造,這其中管道輸水則成為了農田灌溉輸水設施中較為常見的一種方式。管道輸水方式有著諸如快速送水、損漏較少、對環境適應較強、高效便捷等優點,但壓力管道在突然斷水的情況下會出現一種對管道危害較大的現象:水錘現象,也稱作“水擊”。水錘對有壓輸水管道的危害較大,當管道中產生水錘時,管道所要承受的壓力會驟增,當壓力突破管道所能承受的極限壓力時,此時管道有可能會爆裂。文中就針對水錘在管道設計中的防護措施和采取水錘防護措施后的效果(基于Bentley HAMMER的計算分析)做簡要的分析。
2 水錘及水錘預防的幾類主要防護措施
2.1 水錘概述
當有壓管中流速因某種外界原因而發生急劇變化時,將引起管道內部壓強產生迅速交替升降的現象,這種交替升降的壓強作用在管壁、閥門或其他管路元件上好像錘擊一樣,故稱為水錘。
在日常生活中水錘時常會遇到,比如:水龍頭閥門快速開閉時會產生水錘,有時還會聽到管道震動聲。在電站輸水管道中若不能很好處理水錘對管道的影響,輸水管道會產生較大的震動,甚至管道爆裂。與水利工程聯系比較緊密的則是壓力管道輸水工程中對水錘的計算分析,水利工程輸水大多為長距離、大流量、大口徑等特點,由于水錘對輸水管道具有較大的危害性,嚴重時會破壞管道的正常運行,所以為了盡可能將水錘危害降至最低,在工程設計時應對其進行充分分析,并采取必要降低水錘危害的防護措施。
2.2 空氣閥
空氣閥又稱排氣閥或通氣閥,空氣閥在防止水錘危害中是比較常見的管件配置,通過調節管道中的氣體壓力來防止管道高處出現較大的負壓,防止產生彌合水錘,從而降低水錘破壞強度的。當壓力管道中出現水錘現象時,位于管道凸起處的高點往往會出現負壓,導致管道中水流斷裂形成真空,管道中真空度較高的情況下會使水體汽化從而演變成彌合水錘,由于彌合水錘所造成的破壞往往是巨大的,甚至爆管。當管道中出現水錘且產生負壓時,需要盡可能控制負壓強度,通過空氣閥向管道中快速輸送氣體以減緩負壓程度,從而可以大大降低彌合水錘的發生。
空氣閥往往布置在管道高低起伏的凸點位置或者管道壓力相較兩端較小處,且需要放置于管道的上側,閥體周邊應有相應空曠的空間以利于空氣的進出,不得有雜物包裹堵塞閥體。
2.3 緩閉式止回閥
在停泵的瞬間往往會產生水錘波,出現水錘效應。緩閉式止回閥則是利用自身構造,當介質突然中斷后,閥體并不是瞬間關閉,而是分兩階段進行關閉,第一階段快速關閉,此時閥體關閉大部分過流通道,第二階段是緩慢關閉,此階段關閉剩余小部分過流通道,使管道不至快速完全關閉。通過采用緩閉式止回閥可以在保證止回閥功能的前提下消減水錘產生的危害,對保護管道及管件都有較明顯的作用。
2.4 調壓塔
調壓塔是位于地面以上對管道內介質壓力進行調節的一種構筑物。其主要是為了防止由管道壓力變小而導致的介質斷裂分離現象,常設置在管道壓力容易出現負壓的部位。
在輸水管道中,尤其長距離輸水管道沿線地形起伏變化比較大,局部需要穿越障礙物等特定節點,當突然停泵時管線凸起部分易出現負壓從而導致水柱分離,從而對管道及線路上的管件易造成嚴重的破壞,通過在“凸點”設置調壓塔,當管道產生水錘且在“凸點”壓力快速降低時,調壓塔的水可以快速向管道內補水,避免水柱分離和巨大的水錘升壓,降低水錘對管道的破壞作用。
2.5 空氣罐
當前而言利用空氣罐對水錘進行預防的工程實例較少,國內經驗也較少。空氣罐主要分為汽水自然分離式、隔膜式、氣囊式三種。空氣罐運行的主要原理是利用空氣的彈性,既可吸收管道中的正壓,又可向管道內補水來改善管線中的負壓,從而可達到消減水錘的效果。空氣罐往往布置在水泵出口,可結合泵房布置來解決其冬季防凍問題。
空氣罐主要對保護泵房內的儀器設備進行水錘的保護,當水泵突然斷電停泵時,輸水管線中的水壓力將會有急劇變化,當水體的壓力波傳輸到泵房時,空氣罐就利用罐體中的空間來緩沖管道中陡增的水壓力,當管道中的水體由于慣性反向傳播時,空氣罐中的液體就會及時補充管道,避免出現真空,從而抑制了彌合水錘的產生。
3 基于Hammer的水錘預防措施應用分析
3.1 案例概況
工程為地下水補源項目中的一部分,通過本工程設置的泵站將河道的水輸送至補源點,泵站設計流量為0.80 m3/s,設置三臺水泵(兩用一備),單臺水泵設計流量為0.40 m3/s,水泵額定功率為315 kW,水泵楊程為45.00 m。通過水泵將位于高程70.50 m處的水源輸送至高程102.96 m處的補源點,輸水管道采用DN800普通鋼管。
工程通過采用Bentley HAMMER軟件建立輸水管線模型,對輸水管道的穩態和瞬態進行分析模擬,通過對停泵水錘(瞬態)工況的分析,采取相應的水錘預防措施來緩解(或消除)管道的水錘。
3.2 穩態模型分析
工程采用Bentley HAMMER計算分析泵站在穩態運行情況下的管道輸水狀況,此時兩臺水泵同時開啟并持續運行一段時間后,水泵及管道均在額定的工況下運行,此時管道內的水流流態屬于恒定流,管道壓力起點為45.00 m,管道末端自由水頭為8.50 m,管道內的水壓力從水泵后開始至管道末端逐漸減小,此時管道的最大壓力包絡線和管道的最小壓力包絡線是重合的,都均勻降低。由此可知,此時的管道承受的壓力是與設計壓力一致的,管道內的壓力并沒有波動,計算結果詳見圖1。

圖1 穩態分析計算圖
3.3 瞬態模型分析
在管道模型穩態的基礎上,基于工程實例設置瞬間停泵情況下運行工況,兩臺水泵按照設計工況正常運行至某一時刻突然斷電,兩臺水泵同時停泵,此時管道上并沒有安裝任何水錘預防設施,管道上安裝的其余管件都按照設計工況正常運行。
通過Bentley HAMMER對停泵水錘的分析計算,詳見圖2,管道的最大壓力包絡線波動較大,且變化較為劇烈,不同管段的最大壓力水頭也差別較大,另外瞬態工況下管道的最大壓力要比穩態工況下的最大壓力高81.89 m,達到了126.89 m,相當于設計水壓的2.82倍,此時對管道的抗壓要求非常高,管道在運行過程中存在爆管風險。
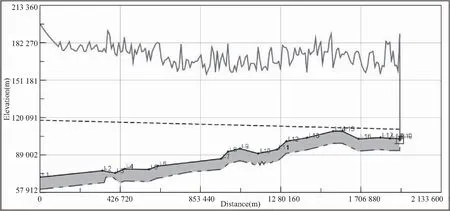
圖2 瞬態分析計算圖
從最小壓力包絡線可以看出,管道沿線均存在一定的負壓,部分管段產生了汽化的現場,使管道產生了彌合水錘,以至于產生了更大的水錘壓力波動,增加了對管道的破壞力。
3.4 預加水錘防護措施
由于文中主要是針對農田水利等常規的輸水管道為對象進行研究的,所以在此次的水錘防護措施案例分析中,選用較為常用、設備簡單、安拆方便、易于后期管理的預防措施,從上文提到的幾種水錘防護措施中選擇空氣閥做為此次案例分析的水錘防護措施進行分析計算。
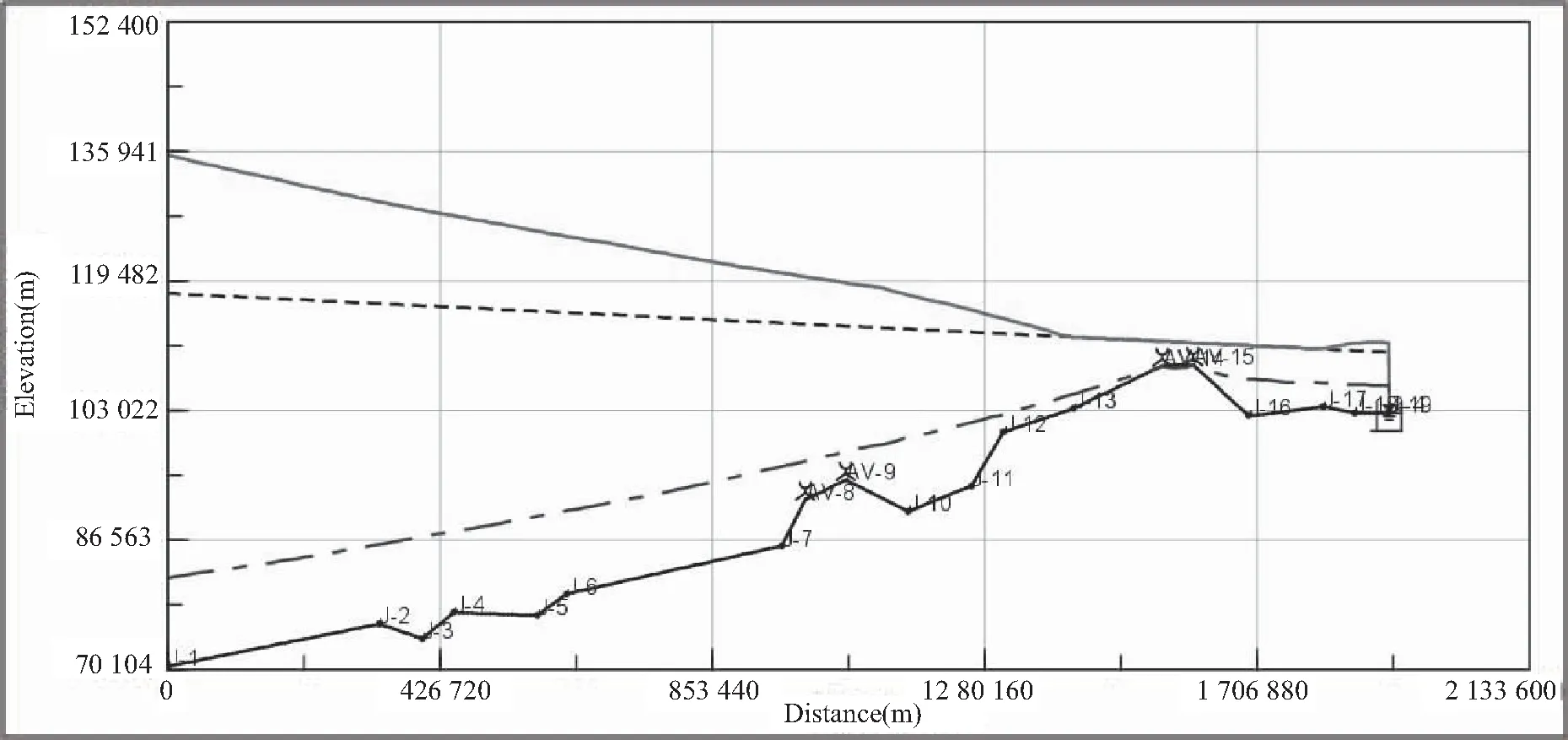
圖3 預加水錘防護措施分析計算圖
工程實例根據輸水線路的高程和空氣閥的工作原理,在輸水線路的凸點選擇節點J-8、J-9、J-14、J-15這四處分別設置空氣閥,空氣閥標號依次為AV-8、AV-9、AV-14、AV-15。當管道中發生水錘后,為了能夠快速的填充管道內的真空,防止液體汽化,同時當管道壓力升高時又能使管道的氣體緩慢的釋放,工程采用空氣閥的進氣口直徑為200 mm,出氣口直徑為15 mm。
管道設置水錘防護措施后,同樣基于Bentley HAMMER軟件對管道的瞬態進行分析模擬,通過瞬態分析計算成果圖可知,管道增設空氣閥之后,管道的最大壓力包絡線由劇烈浮動變成了平順的坡線,且由加防護措施前的最大壓力水頭126.89 m減小至加防護措施后的最大壓力水頭62.11 m。另外管道的最小壓力包絡線均位于管道中心線以上,在瞬態工況下管道中基本消除了負壓情況,避免了管道內因真空度過大而產生汽化。
從工程中可以看出,通過在管道的高點設置空氣閥可以很好地控制水錘的危害,避免輸水管道內壓力的巨大變化,說明空氣閥對抑制停泵水錘是有明顯效果的。
3.5 其他防護措施
僅就空氣閥對停泵水錘的有效防護作用進行了具體分析,對于其它形式的水錘防護措施,基于Bentley HAMMER模型分析結果表明它們對水錘防護均有較好的效果,限于篇幅不再贅述。
4 結語
水錘分析是壓力輸水管道設計中的重要工作,文中首先結合實際工程中幾類典型的水錘防護措施進行分析,分析了各類水錘防護措施的特點以及使用情況。其次基于Bentley HAMMER模型對某一實際工程案例采取的水錘防護措施進行分析,結果表明在壓力輸水管道上設置適當的水錘防護措施可以起到抑制水錘破壞的明顯效果。希望通過對水錘防護及工程案例的分析,對同行進行輸水管線設計時起到一定的借鑒意義,同時也為進一步研究水錘提供參考。

