頁巖油水平井壓裂滲吸驅油數值模擬研究

歐陽偉平，張 冕，孫 虎，張云逸，池曉明

（1.中國石油集團川慶鉆探工程有限公司長慶井下技術作業公司，陜西西安 710018；2.低滲透油氣田勘探開發國家工程實驗室，陜西西安 710018；3.中國石油集團川慶鉆探工程有限公司，四川成都 610051）

頁巖油儲層致密，孔隙喉道小，毛細管力大，對水自發滲吸的作用較強[1]。在頁巖油儲層注水驅油受限的情況下，通過水力壓裂充分發揮壓裂液滲吸驅油作用顯得尤為重要[2]。采用大規模水力壓裂形成復雜裂縫網絡，使頁巖基質與裂縫中的壓裂液充分接觸，壓裂液在毛細管力作用下滲吸至基質內，同時將基質中的油驅替至裂縫中，實現基質裂縫間油水置換，達到壓裂液驅油效果[3]。與常規油氣藏壓裂相比，頁巖油儲層水力壓裂除具有造縫作用外，還具有滲吸驅油和蓄能作用。壓后悶井時間和壓裂液用量是影響滲吸驅油和蓄能作用的關鍵參數，優化悶井時間和壓裂液用量，能夠提高頁巖油儲層壓裂效果。

隨著致密油氣、頁巖油氣開發的不斷深入，滲吸已成為油氣藏工程研究的熱點[4-9]。目前，主要進行了室內滲吸試驗研究[10-18]，分析液體特性、巖石特性等因素對滲吸采出程度的影響。滲吸試驗對于優選滲吸液具有指導作用，但是不能為壓裂液用量、悶井時間等參數的設計提供指導，而壓裂滲吸數值模擬是解決該問題的有效方法。國內外對滲吸油水置換的數值模擬的研究相對較少[19-23]，并且多為滲吸采油機理研究，無法直接應用研究成果和建立的模型優化頁巖油壓裂關鍵參數。

筆者以毛細管力為主要滲吸驅動力，基于體積壓裂矩形裂縫網絡，建立了一種考慮壓裂液注入、悶井滲吸以及開井生產的壓裂頁巖油水平井油水兩相滲流模型，利用控制體積有限元方法求解了該模型的數值解，模擬了滲吸作用下基質-裂縫油水置換的過程，獲得了油水壓力場、速度場、產量以及含水率的動態變化，分析了毛細管力、悶井時間、壓裂液用量、基質滲透率以及縫網復雜程度對滲吸驅油的影響，可為頁巖油水平井壓裂優化設計提供理論依據。

1 物理模型

1.1 復雜縫網描述

水平井分段體積壓裂后每段形成一改造區，其包含復雜裂縫網絡，假定該改造區為矩形，含有主裂縫、次裂縫和支裂縫，主裂縫和次裂縫沿最大主應力方向延伸，主要為張開縫，支裂縫沿最小主應力方向延伸，主要為剪切縫，不同類型裂縫相互正交[24]，如圖1 所示。每段存在1 條主裂縫，次裂縫的數量根據有效開啟簇確定，支裂縫的數量由天然裂縫密度決定。主裂縫、次裂縫和支裂縫的導流能力不同，通常情況下主裂縫的導流能力最大，次裂縫次之，支裂縫最小。

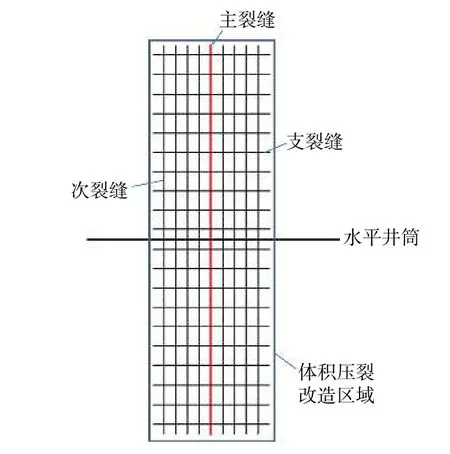
圖1 復雜裂縫網絡描述示意[24]Fig.1 Description of complex fracture networks[24]

1.2 基質-裂縫相對滲透率曲線及毛細管力曲線

表征基質與裂縫油水相滲曲線的Corey 方程為：

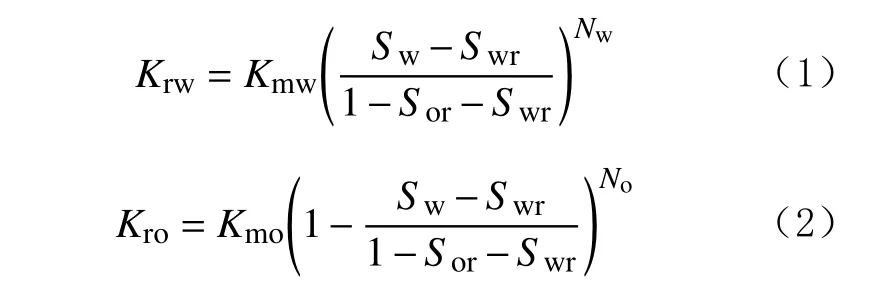
基質的相滲相關系數根據實際巖心的測試結果確定，而裂縫由于滲透率很高，采用標準的裂縫相滲曲線，即束縛水飽和度Swr和Sor殘余油飽和度均為0，冪律指數No和Nw均為1。裂縫滲透率很高，毛細管力很小，因此忽略裂縫毛細管力的影響。基質毛細管力與基質含水飽和度呈冪律關系：

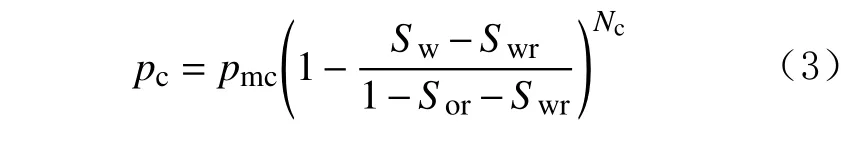
式中：Krw為水相相對滲透率；Kmw為水相最大相對滲透率；Sw為含水飽和度；Swr為束縛水飽和度；Sor為殘余油飽和度；Nw為水相冪律指數；Kro為油相相對滲透率；Kmo為油相最大相對滲透率；No為油相冪律指數；pc為毛細管力，Pa；pmc為最大毛細管力，Pa；Nc為毛細管力冪律指數。

1.3 假設條件

1）原始儲層均質有界，且滲透率具有各向同性，油藏存在油水兩相，流動滿足達西定律，油水黏度、壓縮系數及體積系數隨壓力變化而變化，忽略儲層的應力敏感效應和啟動壓力梯度效應。

2）水平井筒具有無限大導流能力，裂縫具有有限導流能力，流體在裂縫中的流動為一維流動，在基質中的流動為二維流動。

3）毛細管力為滲吸動力，忽略重力和溫度變化對流動及滲吸作用的影響。

4）考慮壓裂液注入、悶井滲吸及開井生產全過程，為了衡量壓裂液蓄能效應，將壓裂過程等效為壓裂液注入至具有復雜縫網的儲層中，引起壓力及含水飽和度的上升，從而為模擬滲吸油水置換過程提供初始條件。

2 數學模型及求解

2.1 數學模型

式中：λ為流度，mD/（mPa·s）；p為壓力，MPa；φ為有效孔隙度；Ct為綜合壓縮系數，1/MPa；Ctw為孔隙壓縮系數與水壓縮系數之和，1/MPa；Cto為孔隙壓縮系數與油壓縮系數之和，1/MPa；t為生產時間，h；Sw為含水飽和度；l為裂縫控制方程的坐標軸，m；wf為裂縫寬度，m；Γ表示邊界；q為流量，m3/d；B為體積系數；h為儲層有效厚度，m；下標o 表示油相，w 表示水相，c 表示毛細管力，m 表示基質，f 表示裂縫，i 表示初始值，I 表示注入，in 表示內邊界，out 表示外邊界。

2.2 模型求解

采用控制體積有限元法（CVFEM）求解上文的模型。控制體積有限元法是一種有限元和有限體積相結合的方法，采用有限元的插值函數和有限體積的數值計算格式，無需二次重建網格，可直接利用有限元網格，網格更靈活、精度更高，且具有有限體積局部守恒性特征，非常適合油藏油水兩相流數值模擬。

基質壓力控制方程中時間導數項的差分格式為：

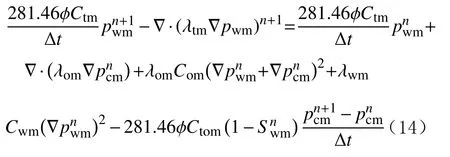
基質飽和度控制方程中時間導數項的差分格式為：

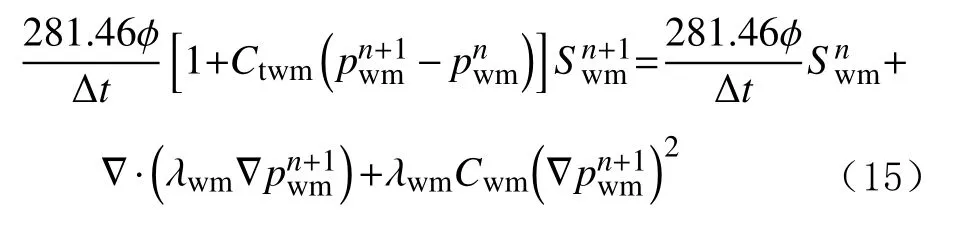
裂縫壓力控制方程中時間導數項的差分格式為：

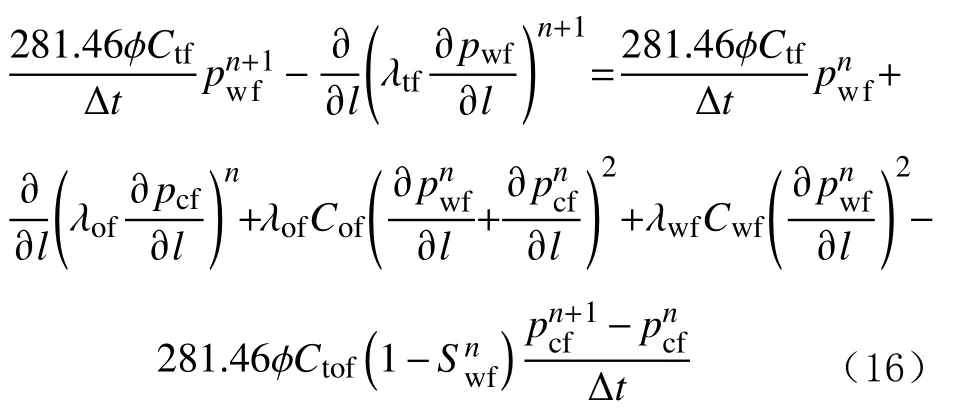
裂縫飽和度控制方程中時間導數項的差分格式為：

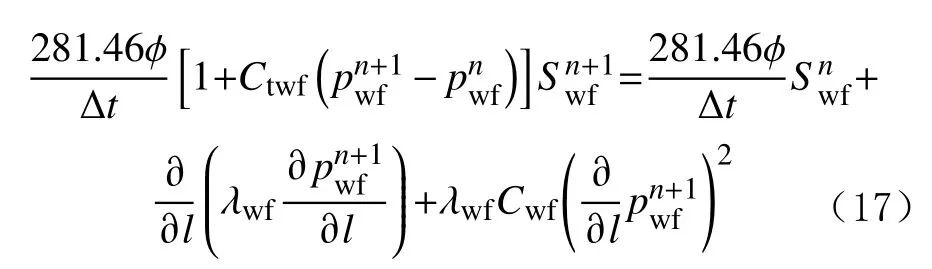
利用非結構化網格離散技術對包含復雜網絡裂縫的計算區域進行Delaunay 三角網格剖分，網格與裂縫網絡完全匹配。連接三角形各邊中點與三角形中心點，形成CVFE 網格，將裂縫與基質分開（見圖2）。以單元節點為中心，對式（14）—（17）在CVFE 網格單元上積分，分別形成基質單元剛度矩陣和裂縫單元剛度矩陣，并根據單元節點信息，組成壓力方程的總剛度矩陣及飽和度方程的總剛度矩陣，采用隱壓顯飽的方式迭代求解，詳細的求解方法及步驟可參考文獻[25]。

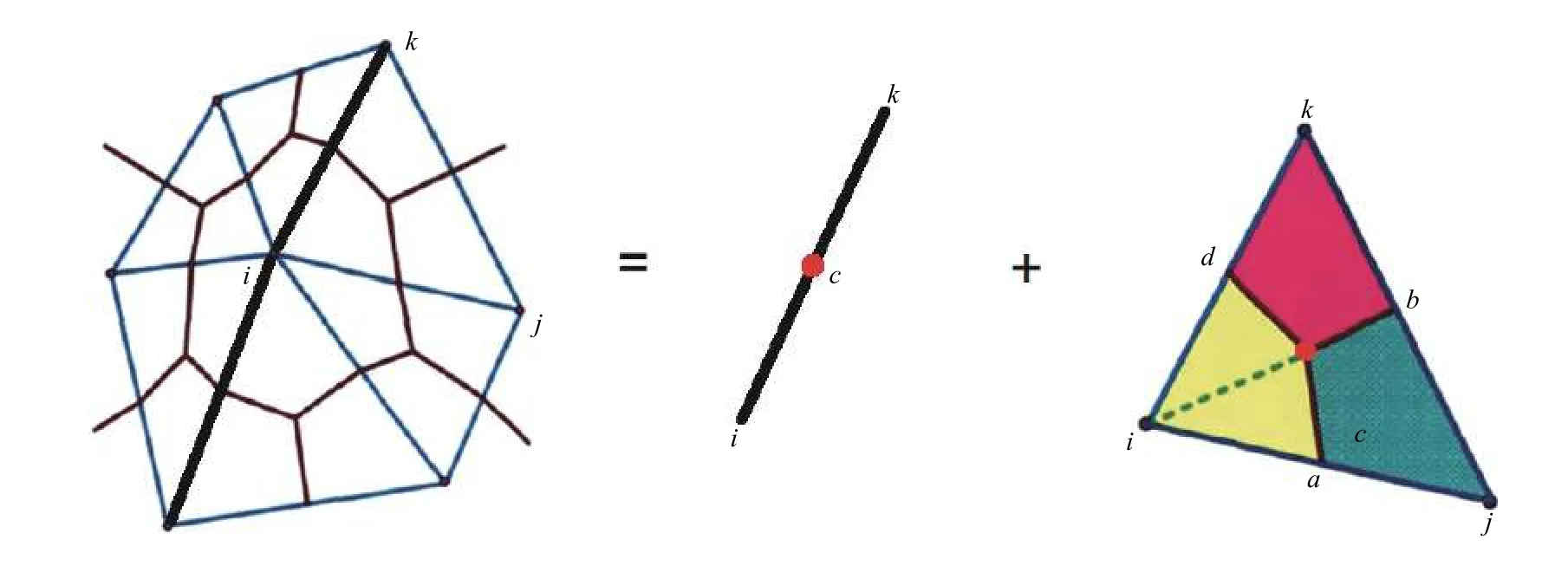
圖2 裂縫基質的CVFE 網格示意Fig.2 CVFE meshes of the matrix and fractures

3 計算結果及分析

3.1 壓裂滲吸驅油特征

假定儲層初始壓力為17 MPa，滲透率為0.1 mD，溫度為65 ℃，有效厚度為10 m，孔隙度為10%，初始含水飽和度為0.45；水平井各壓裂段的間距為60 m，井間距為400 m，因此單段控制面積為24 000 m2；單段多簇壓裂液用量為857 m3，假定70%進入了目的層，即注入目的層液量為600 m3，有效開啟3 簇，其中主裂縫1 條，次裂縫2 條，主次裂縫半長均為170 m，支裂縫10 條，縫長均為48 m，主裂縫導流能力為500 mD·m，次裂縫導流能力為200 mD·m，支裂縫導流能力為100 mD·m；壓后悶井100 d 后按照先定產（單段產量4 m3/d）降壓再定壓（7 MPa）降產的方式生產。利用上文建立的油水兩相滲流模型模擬不同毛細管力下單壓裂段第1 年的生產動態，結果如圖3和圖4 所示。

由圖3 可以看出，毛細管力越大，產油量越大，表明毛細管力滲吸作用具有明顯的增產作用。此外，隨著毛細管力增大，開井生產時的含水率及整個生產過程中的平均含水率都呈下降趨勢。壓后悶井過程中，在壓裂液滲吸驅油作用下，裂縫中的水進入基質，置換出基質中的油，導致基質內含水飽和度升高，裂縫內含水飽和度降低，從而使開井生產時的含水率降低，在毛細管力足夠大、悶井時間足夠長的情況下，放噴排液階段即可“見油”。

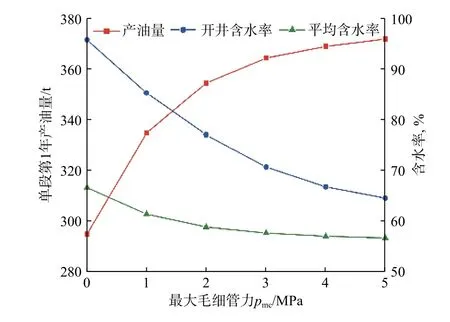
圖3 單段在不同毛細管力作用下的產油量及含水率Fig.3 Oil production and water cut of single stage under different capillary forces

圖4 為最大毛細管力3 MPa 下悶井75 d 時裂縫周圍水相和油相的壓力場及速度場（速度場箭頭代表流動方向，箭頭長度代表速度大小）。由圖4 可以看出：裂縫內水相的壓力大于基質水相的壓力，水從裂縫流入基質（見圖4（a））；基質油相的壓力大于裂縫內油相的壓力，油從基質流入裂縫（見圖4（b））。由于基質與裂縫中的含水飽和度不同，引起毛細管力差異，形成滲吸驅動力，使基質與裂縫發生油水置換。從圖4 還可以看出，主裂縫周圍油水兩相的流速較大，次裂縫及支裂縫附近油水兩相的流速較小，遠離裂縫區域油水兩相的流速最小。此外，從油水相的壓力場可看出，壓裂液的注入能夠大幅度提高儲層壓力，蓄能作用明顯，該算例儲層壓力從初始的17 MPa 提高至開井生產時的31 MPa。

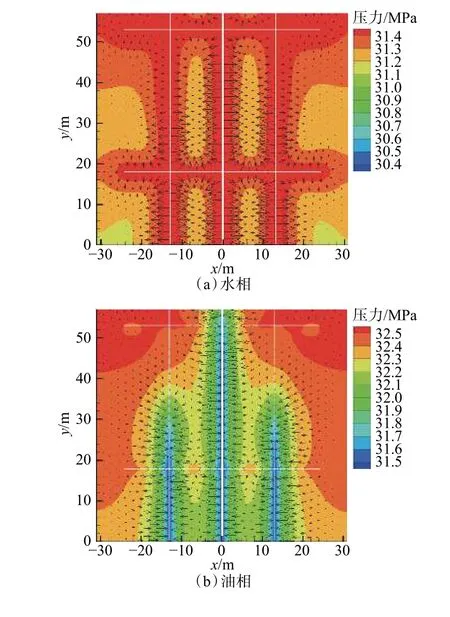
圖4 悶井75 d 時裂縫周圍油水相的壓力場及速度場Fig.4 Pressure field and velocity field of the oil phase and water phase around the fractures on the 75th day of shut in

3.2 悶井時間優化

采用與3.1 節相同的儲層參數，計算不同毛細管力條件下不同悶井時間單段第1 年的產油量，結果見圖5。由圖5 可以看出：對于無毛細管力的儲層，儲層內不存在滲吸作用，壓后悶井產油量不能增加，因此對于常規中高滲透儲層（毛細管力很小），是否悶井對產油量的影響非常小；對于具有毛細管力的儲層，隨著悶井時間增長，產油量升高，但升高幅度逐漸減小，且毛細管力越大，升高幅度減小的速度越快。這主要是因為毛細管力越大，滲吸作用越強，在基質滲透率不變的條件下，油水置換速度越快，最優悶井時間越短。假定以悶井1 d 單段產油量升高幅度大于0.15 t 為設計標準，優化設計悶井時間，該算例下最大毛細管力為1，2，3，4 和5 MPa時，最佳悶井時間分別為126，92，75，61 和56 d。

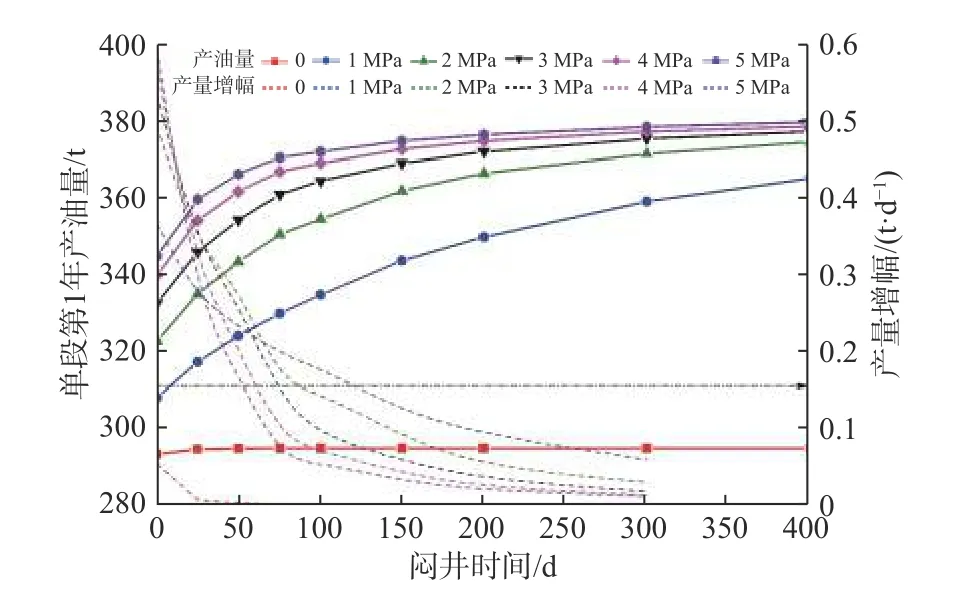
圖5 悶井時間對單段產油量的影響Fig.5 Effect of shut-in time on the oil production of single stage

3.3 壓裂液用量優化

注入壓裂液達到一定量后縫網不再明顯增加，因此假定縫網等其他參數不變，考慮壓裂液用量對滲吸驅油和蓄能的影響，模擬計算最大毛細管力為3 MPa、注入不同量壓裂液、悶井100 d 下單段第1 年的產油量和含水率，結果見圖6。由圖6 可以看出，隨著壓裂液用量增大，產油量和含水率均升高，但產油量的升高幅度逐漸減小，而含水率升高幅度逐漸增大。其原因在于，壓裂液用量增大，導致基質與裂縫的含水飽和度差異增大，造成滲吸驅油壓差增大，因此產油量升高，但是當注入壓裂液的量超過了儲層基質的滲吸能力，有些壓裂液滯留在裂縫內無法進入基質，只能通過生產產出，造成含水率升高。算例中壓裂液用量達到1 300 m3之后，含水率急劇升高，產油量升幅明顯減小，因此該算例壓裂液的最佳用量為1 300 m3。

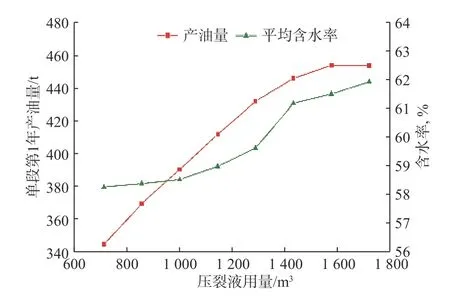
圖6 壓裂液用量對產油量及含水率的影響Fig.6 Effect of fracturing fluid volume on oil production and water cut

3.4 基質滲透率的影響

模擬計算最大毛細管力為3 MPa、壓裂液用量為1 300 m3時，不同基質滲透率單段第1 年產油量，結果見圖7。由圖7 可以看出，基質滲透率越高，產油量越高，最佳悶井時間越短，若按照同3.2 節相同的設計標準，基質滲透率為0.05，0.10 和0.30 mD 時，最優悶井時間分別為151，94 和45 d。其主要原因是毛細管力相同時，基質滲透率越高，油水流動的速度越快，基質與裂縫之間的油水置換速度也越快，最佳悶井時間也越短。

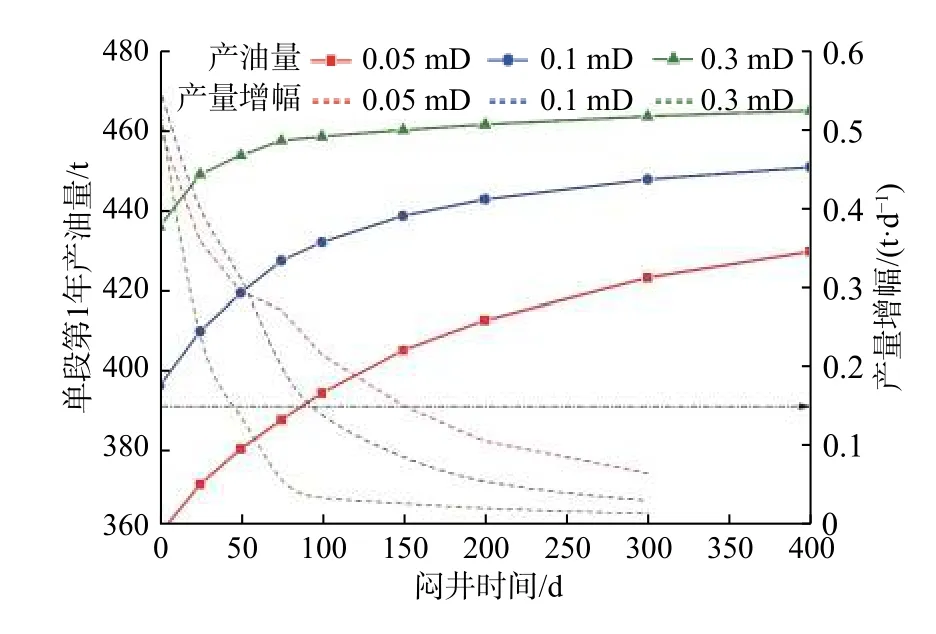
圖7 基質滲透率對單段產油量的影響Fig.7 Effect of matrix permeability on the oil production of single stage

3.5 縫網復雜程度的影響

模擬計算有效壓裂簇分別為1 簇、3 簇和5 簇時單段第1 年的產油量，結果見圖8。1 簇無支裂縫，3 簇有10 條支裂縫，5 簇有14 條支裂縫，代表縫網復雜程度從低到高。由圖8 可以看出，縫網復雜程度越高，產油量越高。其原因是：1）縫網越復雜，流動阻力越小，產油量越高；2）縫網越復雜，裂縫與基質間的滲吸面積越大，滲吸增油量越大。由于單簇裂縫與基質的接觸面積太小，滲吸作用很弱，造成滲吸驅油量很低，如圖8 中的紅色虛線所示。對比3 簇和5 簇的產油量增幅可知，5 簇產油量增幅下降速度更快，其滲吸作用更強，最佳悶井時間更短，說明縫網復雜程度越高，滲吸面積越大，滲吸速度越快。

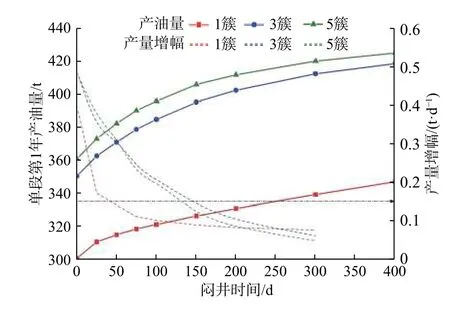
圖8 縫網復雜程度對單段產油量的影響Fig.8 Effect of fracture network complexity on the oil production of single stage

4 結論

1）數值模擬結果表明：壓后悶井階段裂縫水相壓力大于基質水相壓力，水從裂縫流入基質，而裂縫油相壓力小于基質油相壓力，油從基質流入裂縫。基質與裂縫的含水飽和度不同，引起毛細管力，形成滲吸驅動力，使基質與裂縫發生油水置換。主裂縫周圍油水相的流速均較大，次裂縫及支裂縫附近油水相的流速較小，遠離裂縫區域油水相的流速均最小，說明油水置換主要發生在裂縫與基質的接觸面。

2）毛細管力越大，最佳悶井時間越短，開井含水率和生產平均含水率越低，滲吸增產作用越明顯；壓裂液用量增大，不僅能提高儲層壓力，起到蓄能效果，還可使基質與裂縫的含水飽和度差異程度增大，滲吸驅油產量升高，但同時也會引起含水率升高，可通過含水率和產油量增幅優化壓裂液用量。

3）最佳悶井時間主要受毛細管力、基質滲透率及縫網復雜程度的影響，其中毛細管力和基質滲透率決定油水置換的速度，而縫網復雜程度決定了油水置換的接觸面積。毛細管力越大、基質滲透率越高、縫網越復雜，最佳悶井時間越短。

4）文中建立的滲吸油水兩相滲流模型有助于提高壓裂頁巖油水平井產量的預測精度，同時可為優化頁巖油水平井壓裂液用量、悶井時間等關鍵參數提供依據。