波浪沖洗對多浮冰耦合運動影響特性研究

朱仁慶，張 曦，李志富

（江蘇科技大學船舶與海洋工程學院，江蘇鎮江 212001）

0 引 言

有證據表明北極地區海冰覆蓋面積隨著全球氣候變化整體呈現出減小趨勢，使得北極航線的開通和自然資源的大規模開發成為可能[1]。冰緣區處于開闊水域和海冰的交界處，受波浪影響十分顯著。掌握冰緣區內海冰與波浪相互作用的規律，對于正確認識冰區內波浪傳播特性以及合理開發北極具有重要的指導意義。

現階段研究波浪與海冰的相互作用主要采用模型試驗和數值模擬的方法。在模型試驗方面，Montiel等（2013）[2]開展了浮冰在波浪中運動的試驗研究，并對理論預報結果與實測數據之間差別的可能來源進行了分析。Bennetts 和Williams（2015）[3]利用理論與試驗相結合的方法，對波浪經冰區的傳播規律進行了研究，并發現散射是造成波能衰減的主要原因。Bennetts等（2015）[4]通過試驗研究發現，波浪透射能量一般隨著入射波波陡的增加而減小，并且在入射波波長等于浮冰特征長度時達到最小極值。Yiew等（2016）[5]對規則波中浮冰的三自由度運動響應進行了試驗分析，發現波浪沖洗現象可以明顯抑制浮冰的運動響應。Yiew 等（2017）[6]利用試驗研究了在不同波長和波高的規則波激勵下兩個薄圓盤的運動，并且基于Slope sliding 理論預測了圓盤的運動，其中浮冰只限于單一方向水平運動。在數值模擬方面，Susan等（2001）[7]實測了巴倫支海浮冰的六自由度運動響應，并通過譜分析方法研究了浮冰在不同波頻下的幅值特征。Bennetts 和Squire（2009）[8]建立了冰緣區內波浪的三維散射模型，研究發現浮冰厚度，浮冰行對齊方式、行間距以及浮冰半徑都對波浪的反射現象有影響。隨后，Bennetts 等（2010）[9]利用冰緣區內的三維波浪散射模型預測了波浪衰減率，研究發現，波浪衰減與入射波角度呈指數關系，其中斜入射波衰減最快。浮冰形狀、分布以及其吃水對波浪衰減的影響很小。Montiel等（2015）[10]給出了一種多個浮冰作用下的波浪散射模型，通過改變浮冰隨機分布密度證明了單個浮冰是影響波浪散射的主要因素，僅需三個浮冰即可解釋浮冰的多重散射效應。倪寶玉等（2019）[11]利用Fluent軟件研究了多浮冰與波浪的相互作用，研究發現浮冰數目的增多抑制了浮冰運動，浮冰的存在一定程度上阻礙了波浪運動。

目前，對于波浪與多浮冰作用問題，盡管已有相關研究，但是有關多浮冰耦合運動過程中的波浪沖洗效應研究還十分有限。基于此，本文建立了二維粘流數值水池，模擬了波浪作用下多浮冰的耦合運動，并重點對比研究了不同浮冰數目條件下波浪沖洗冰體表面現象對浮冰垂蕩、縱搖運動的影響規律。

1 數值計算方法

1.1 控制方程

為了有效計及湍流影響，在求解流體控制方程時將控制方程中的各項分解為時間平均值和相對于這些平均值的脈動值兩部分，即雷諾時均方程組，其表達式如下：

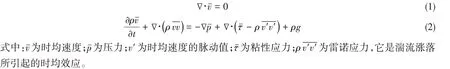
1.2 數值造波理論

本文采用速度入口造波方式完成造波任務，在入口處采用松弛區域消波技術，以消除浮冰引起的波浪反射對造波的影響；出口處采取阻尼消波方法來達到消波目的。本文選取斯托克斯五階波[12]，以精確模擬冰體上浪等非線性現象。在造波邊界處的速度和波面瞬時升高滿足以下條件：

x方向速度為

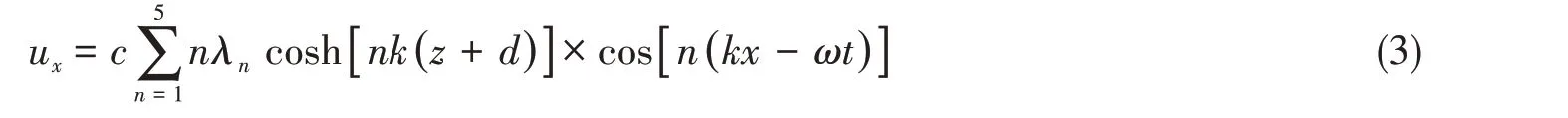
z方向速度為

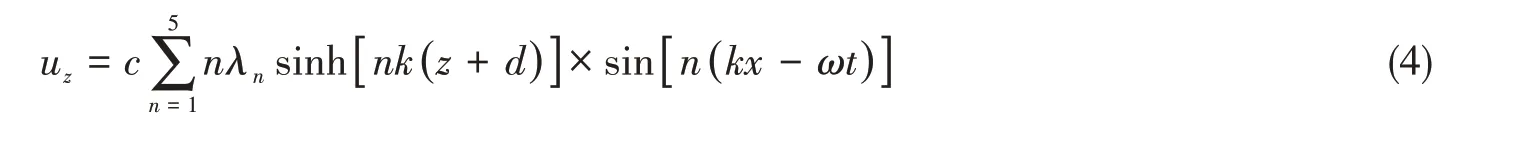
波面瞬時升高為

式中各系數如下：

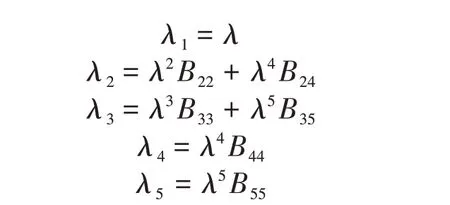
其中，ω、d和k分別為圓頻率、水深和波數。定義c=coshkd、s=sinhkd，其余各項系數參見文獻[13]。

在入口處采取松弛區域消波方法，通過在動量方程中添加源項q?使得波浪在近速度入口時逐漸變為入射波，源項表達式如下：

式中：γ為強迫系數，其中γ= -γ0cos2( πx*/2 )，它使得在指定入口消波區內強迫消波的力度逐漸變大；?為數值模擬計算出的動量輸運方程的結果；?*為原動量方程的理論解。

在出口處應用阻尼消波的方法，通過在波浪運動的垂直方向添加阻尼實現消波，其阻尼項表達為

為適應未來城市化加速發展、工業化深化發展、土地、耕地和水等資源日益短缺、國內人口流動規模不斷加大、國際游客不斷增多等的態勢，新世紀我國養豬業將朝著優質、高效、安全的目標發展，養豬生產將以適度規模化、規范化、標準化、生態循環經濟模式為主體，多項技術的綜合配套利用是提高養豬業整體生產水平和效益的關鍵。下面將從育種、營養、豬肉安全生產等方面探討我國新世紀養豬業的發展。

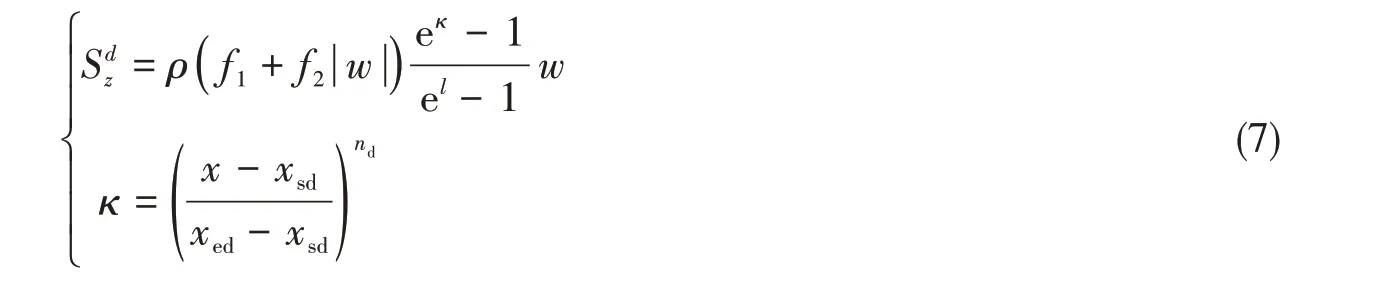
式中：xsd為消波區起始位置的坐標；xed為消波區結束位置的坐標；f1、f2、nd為阻尼消波模型的參數；w為坐標軸z方向的速度。

1.3 浮體運動方程

在隨浮體進行平移和旋轉的運動坐標系中，浮體的運動方程為

式中，m為浮體質量，I為浮體轉動慣量，f為流體施加于浮體的合外力，M為浮體受到的合外力矩。

2 算例設置

2.1 二維模型和網格劃分

本文選用RKE 2L湍流模型[14]來對控制方程進行封閉求解。離散方法選用有限體積法，采用PIMPLE 算法將壓力速度進行耦合。采用VOF 法對自由液面進行捕捉。如圖1所示，水池左邊界、上邊界以及下邊界設置為速度入口條件；前后兩側邊界設置為對稱邊界條件；右側邊界設置為壓力出口條件。入口消波區和出口消波區長度分別取為一個波長長度。

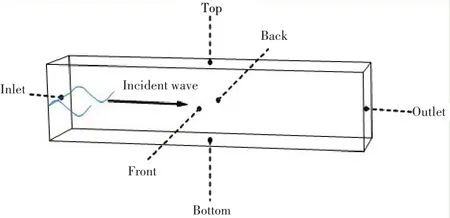
圖1 流域邊界Fig.1 Sketch of the computational domain

計算區域長10.5 m、高0.8 m，水深0.5 m。在水池中加入浮冰模型，如圖2 所示，處于中間位置的浮冰放置于距離入口4.25 m 處。位于中間浮冰的位置不變，在中間浮冰兩側以對稱的方式逐漸增加浮冰數目，其中相鄰浮冰中心間隔0.75 m。本文中的浮冰運動被視為剛體運動。如圖3所示，浮冰模型采用了兩種簡化模型，浮冰模型長為0.5 m，冰厚為0.05 m，浮冰密度為600 kg/m3，入水深度為0.03 m。為了防止流體沖洗冰體表面，在圓柱上表面增加了一圈薄護欄，護欄高度為0.05 m，理論研究表明添加護欄對浮冰運動的影響可忽略不計[4]。波浪參數設置如表1所示。

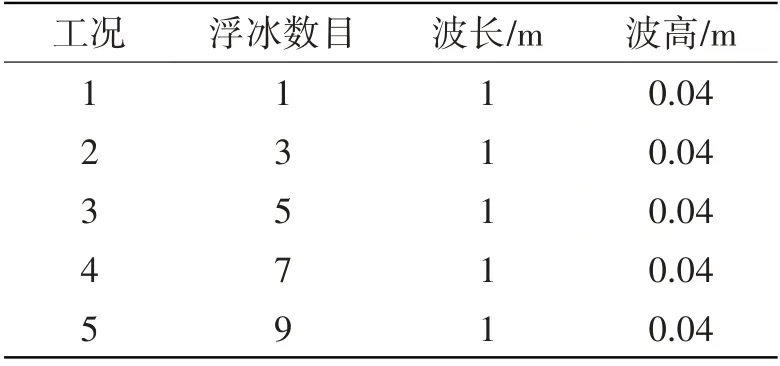
表1 波浪參數Tab.1 Wave parameters

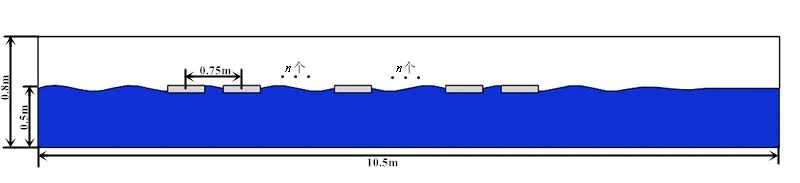
圖2 二維數值水池Fig.2 Two-dimensional numerical wave tank

圖3 二維浮冰模型Fig.3 The geometry of two-dimensional ice floes

本文采用動網格技術來模擬浮冰運動。為了精確地模擬浮冰以及波浪運動，在數值水池中對自由液面區域進行加密，并且對浮冰運動區域也進行了網格加密。圖4為工況2的網格示意圖。

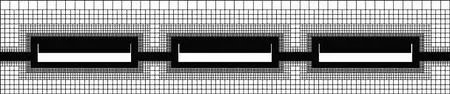
圖4 動網格示意圖Fig.4 Diagram of the dynamic mesh method

2.2 網格及時間步收斂性分析

結合極地冰緣區歷史波高和周期的概率分布，以及波浪參數（見表1）與浮冰直徑的無量綱比例關系，在給定波浪要素的前提下，研究不同浮冰數目條件下的冰體耦合運動，其中波長為1 m，波高為0.04 m。

選擇數值水池中處于中間浮冰所在位置作為液面升高探測點，選取給定的入射波波浪要素來記錄該點處液面升高時歷，與斯托克斯五階波理論解進行對比。對于波幅（A）較小的波浪來說，沿著波高（H）方向的網格大小（Δx）對造波效果起著決定性作用。因此，本文選取自由液面波高方向三組不同網格大小，設置不同時間步（Δt）來對造波效果進行收斂性分析，波高方向網格大小分別為Δx=H/5，Δx=H/10，Δx=H/15。同時，沿波長方向的網格分布與波高方向網格分布之比為4:1。具體網格與時間步設置如表2所示。

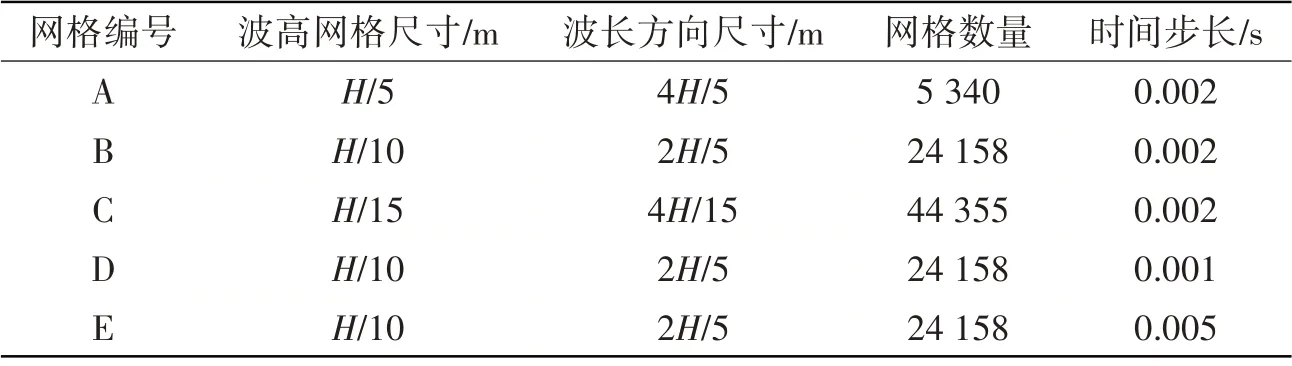
表2 網格與時間步設置Tab.2 Settings of grid size and time step

3 計算結果及分析

浮冰在波浪中的耦合運動與浮冰之間的分布形式密切相關。為了進一步探索浮冰與入射波相互作用時，浮冰數目對耦合垂蕩、縱搖運動響應的影響，本文對不同浮冰數目工況中處于中間位置的浮冰垂蕩（η3）和縱搖（η5）運動響應進行了頻譜分析。

3.1 遮蔽效應

為了消除波浪沖洗冰體表面的影響，通過模擬有護欄浮冰在波浪中的運動來分析其與波浪的相互作用。在研究中發現，當流體域中存在多個浮冰時，不同位置處的浮冰個體與波浪的相互作用存在差異。位于前側的浮冰阻礙了波浪的運動，使得位于后側的浮冰與波浪的相互作用較弱。

圖7 是工況3 的一個周期內運動示意圖，位于前側的浮冰與波浪發生了較強的相互作用，表現出較劇烈的搖蕩運動。位于后側的浮冰運動狀態相較于前側的浮冰，其搖蕩運動較小。同樣地，后側浮冰窄縫內的波浪運動相比于前側浮冰窄縫內的波浪運動逐漸趨于平坦，波浪產生明顯衰減。

圖7 一個周期的浮冰運動Fig.7 Motion response of ice floes in one wave period

圖8提取了各個工況中位于中間位置浮冰的垂蕩和縱搖運動，在波浪激勵頻率下，圖8（a）中浮冰的垂蕩運動幅值隨著浮冰數目的增多而減小。隨著浮冰數目的增多，海冰對波浪的傳播產生越來越嚴重的阻礙作用，使得波浪發生明顯的耗散，浮冰接收到的波浪能量也因此發生很大程度的衰減，導致浮冰受到波浪的作用較小。隨著浮冰個數的減小，波浪受到的傳播阻礙變小，波浪傳遞給浮冰的能量變大，浮冰與波浪的相互作用變強，因此使得浮冰在波浪激勵頻率下的運動變大。同樣地，圖8（b）中，隨著浮冰數目的增多，波浪激勵作用對中間位置的浮冰縱搖運動影響變小，其縱搖幅值減小，縱搖運動的變化趨勢與垂蕩運動變化趨勢相似。

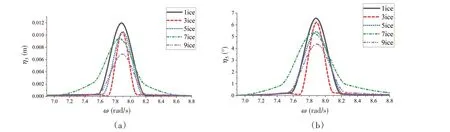
圖8 不同浮冰數目下有護欄浮冰運動幅值對比Fig.8 Motion amplitude of the middle ice floe with barrier at different ice floe numbers

因此，由上述分析可知，由于多浮冰與波浪的相互作用以及多浮冰的耦合效應，浮冰對波浪具有一定的遮蔽和衰減作用。隨著浮冰數目的增多，位于中間位置的浮冰運動相應變小。浮冰窄縫距離波浪入口越遠，窄縫間的波浪運動也趨于平緩。

3.2 波浪沖洗現象

在真實海況中，海冰受到波浪的作用會發生劇烈運動，并出現一定量的流體涌上冰體表面的現象。本文通過數值模擬發現，由于波浪沖洗現象的出現，無護欄浮冰運動與有護欄浮冰運動有明顯差異。隨著浮冰數目的增加，處于中間位置的浮冰受到的波浪沖洗程度也有減小。

圖9 分別對應處于工況1 和工況5 中間位置浮冰冰表面所受到的波浪沖洗現象。圖9（a）對應工況1，浮冰上表面明顯被流體覆蓋，并且入射波浪有再次沖洗的趨勢，表現出較強的波浪沖洗現象；圖9（b）對應工況5，浮冰上表面幾乎沒有流體覆蓋，波浪相較于工況1 較平緩，沒有呈現上浪趨勢，相較于前者，工況5沒有出現波浪沖洗現象。

圖9 不同浮冰數目工況中波浪沖洗冰體表面過程Fig.9 Overwash phenomena at different ice floe numbers

圖10中給出了工況2的浮冰垂蕩、縱搖的頻譜分析圖。波浪激勵頻率下，無護欄浮冰的垂蕩運動幅值小于有護欄浮冰垂蕩運動幅值。在縱搖運動響應中，其與垂蕩運動響應具有相同的趨勢，無護欄浮冰在波浪激勵頻率處的運動幅值也遠遠小于有護欄浮冰。表3提取了各個工況中波浪激勵頻率下的浮冰運動幅值。經過對比發現，無護欄浮冰與有護欄浮冰出現幅值差異的原因主要是波浪沖洗冰體表面，堆積在冰體表面的水阻礙了浮冰的運動。

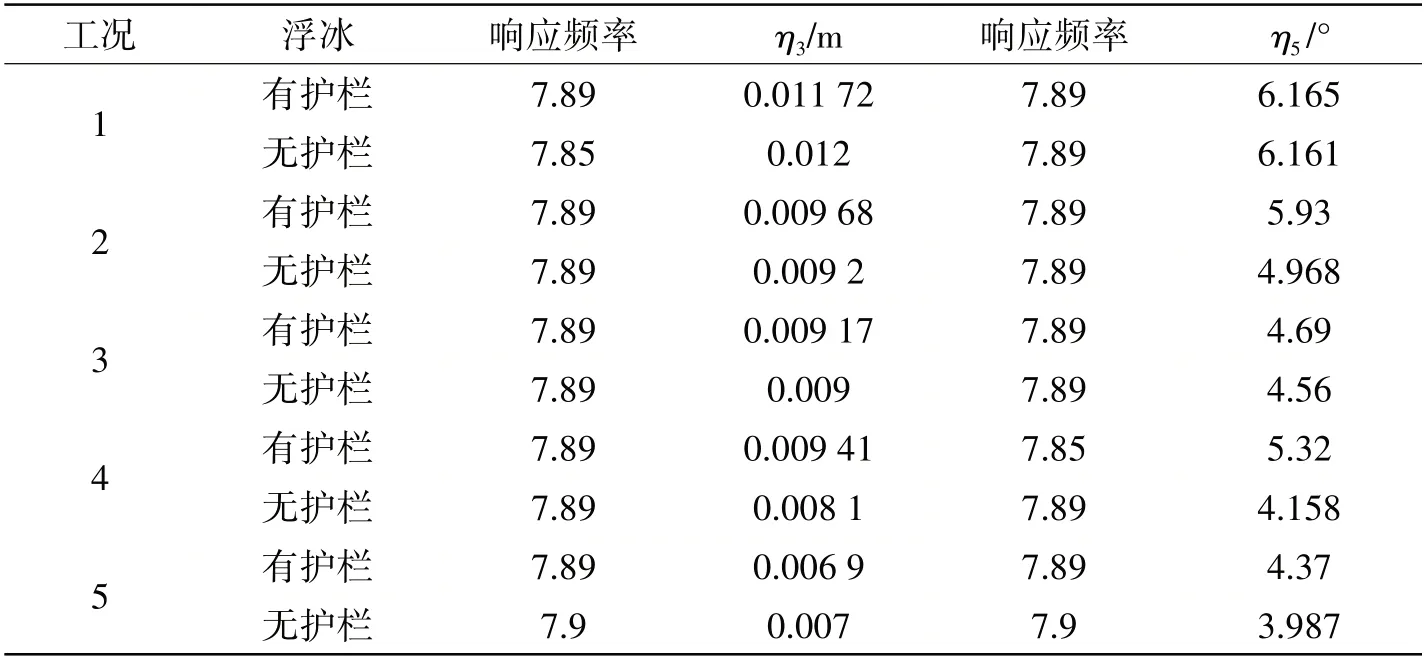
表3 中間浮冰運動幅值Tab.3 Motion amplitude of the middle ice floe

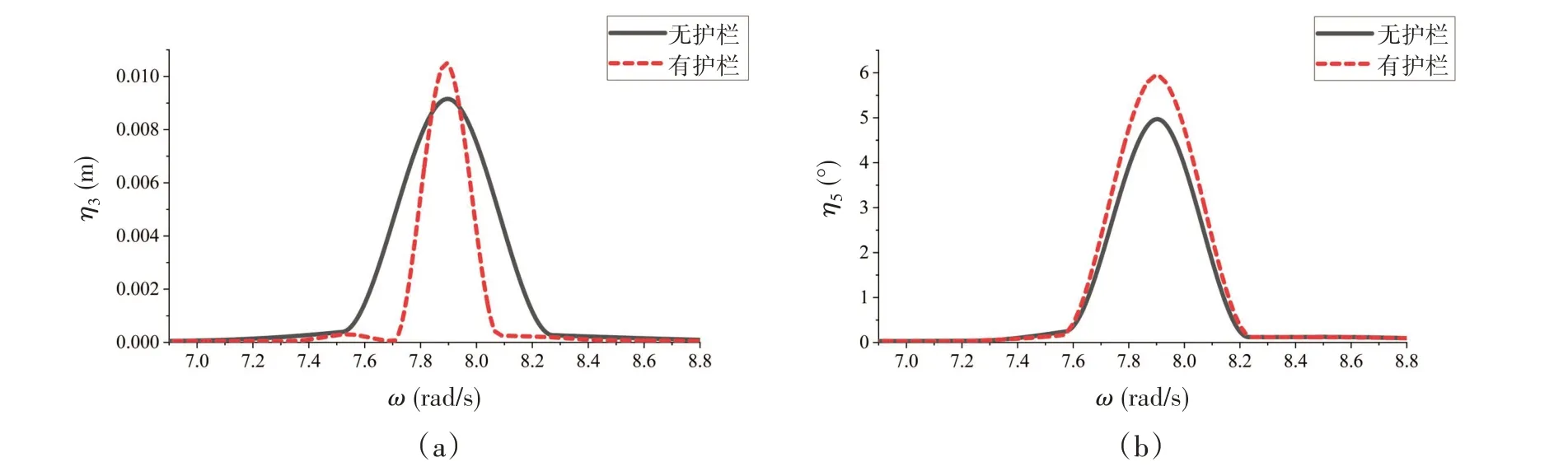
圖10 工況2中間浮冰運動幅值對比Fig.10 Motion amplitude of the middle ice floe corresponding to Case 2

圖11給出了工況1至工況5中位于中間位置無護欄浮冰的垂蕩、縱搖運動響應頻譜分析圖，即不同浮冰數目工況中出現的波浪沖洗現象對中間位置浮冰運動的影響。由圖11可知，隨著浮冰數目的增加，浮冰對波浪的遮蔽作用以及衰減作用變強，中間位置浮冰接受到的波浪能量減少，導致波浪激勵頻率下浮冰的垂蕩運動與縱搖運動減小。當浮冰數目較少時，由于存在較明顯的波浪沖洗現象，浮冰運動幅值差異較大。隨著浮冰數目的增多，波浪能量衰減較大，浮冰受到的波浪沖洗現象減小，浮冰運動幅值減小。

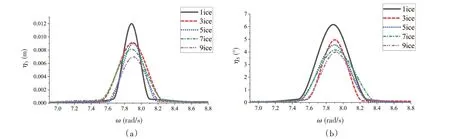
圖11 不同浮冰數目對無護欄浮冰的運動響應影響Fig.11 Comparison of the motion amplitudes of the ice floe without barrier at different ice floe numbers

綜上可知，無護欄浮冰由于受到波浪沖洗的作用，其運動幅值明顯小于有護欄浮冰。同時，隨著浮冰數目增加，中間浮冰受到的波浪沖洗現象減弱，該浮冰運動幅值的差異也逐漸縮小。

4 結 論

本文通過建立二維數值水池模擬了兩種浮冰模型（帶護欄/無護欄）在波浪中的運動，分析了有/無波浪沖洗現象對浮冰垂蕩與縱搖運動的影響。研究發現：

（1）由于多浮冰與波浪的相互作用以及多浮冰的耦合相互干擾，浮冰對波浪具有一定的遮蔽和衰減作用，隨著浮冰數目的增多，位于中間位置的浮冰運動相應變小，浮冰窄縫距離波浪入口越遠，窄縫間的波浪運動也趨于平緩；

（2）無護欄浮冰由于受到波浪沖洗的作用，其運動幅值明顯小于有護欄浮冰。同時，隨著浮冰數目增加，中間浮冰受到的波浪沖洗現象減弱，該浮冰運動幅值的差異也逐漸縮小。

本文通過二維數值模型研究了浮冰有/無上浪現象對浮冰運動的影響，研究發現，上浪導致的沖洗現象對浮冰運動具有一定的抑制作用，隨著浮冰數目的增多，波浪沖洗現象減弱，其對浮冰運動的抑制作用也減弱。為了考慮沖洗現象對浮冰運動的影響，可參照本文采用有/無護欄浮冰模型來模擬浮冰的運動。本文計算中采用的加護欄的浮冰模型對于研究浮冰在波浪下的運動具有一定的參考意義。此外，當流場和浮冰運動具有明顯三維特征時，可參照本文建立的分析方法在三維物理場內開展相關研究。另外，對于大尺度浮冰還需進一步考慮其在流場動壓力作用下的彈性效應與破碎。