基于雙三相 PMSM車載充電器的雙環滑模控制

顧鴻赟，李 巖，劉陵順

(1.海軍航空大學 航空基礎學院，煙臺 264001；2.中國人民解放軍92925部隊，長治 046000)

0 引 言

近年來，新能源汽車成為了汽車行業重點關注的新興產業。軍事領域中，混合動力戰車和多電飛機也有了長足的發展。低碳減排的電能驅動，對電池的快速充電提出了更高要求[1]。根據充電方式的不同，可將充電器分為非車載充電器和車載充電器，其中車載充電器加裝在車體內部，雖然體積質量受限、充電功率較小，但成本較低，可用工頻單相或三相電源直接充電，使用更為方便[2]。輕便型大功率車載充電器成為了未來發展趨勢。

在車載充電器拓撲結構方面，文獻[3-5]對多相電機的驅動充電集成一體化進行了研究，介紹了不同類型的驅動充電一體化拓撲結構和充電模式的工作原理。文獻[6-7]提出了采用九開關電源變換器的六相永磁同步電機驅動充電一體化拓撲結構，電力電子元件數量相比六相變換器又減少了三分之一。在充電器控制策略方面，文獻[8-9]采用傳統PI控制策略。這類控制策略的穩定性依賴于電機模型和系統參數，易受外界干擾影響。而滑模變結構控制實質上屬于非線性控制算法，具有動態響應速度快、自適應能力強、穩定范圍寬等優點[10-14]。在滑模控制趨近律中，積分趨近率能夠減小穩態誤差，抑制抖振[15]，更適用于本文的車載充電器充電模型。

為提高車載充電器的抗干擾能力和動靜態性能，減少電力元件的損耗，本文采用驅動充電一體化拓撲結構，設計了充電模式下電壓電流雙環滑模控制策略，結合SVPWM技術實現電力開關控制。通過仿真，驗證了雙環滑模控制的車載充電器比傳統的PI控制系統具有更優的穩定性、魯棒性和動態性能。

1 車載充電器的拓撲結構及工作原理

1.1 驅動/充電一體化的車載充電器工作原理

本文驅動/充電一體化拓撲結構如圖1所示。此拓撲結構由車體內部的六相永磁同步電機(具有兩個獨立的中性點)、九開關變換器和四個接觸器(S1～S4)組成，由車體外部的工頻三相交流電源供電。當系統工作在充電模式下，接觸器 S1～S4斷開，外部的三相電源接入車體，三相電源的A相連接電機a、d相，B相連接b、f相，C相連接c、e相，九開關變換器的中位開關Gm1～Gm3始終導通(簡化為短路)。這種連接方式讓兩套定子繞組中產生一對大小相等、方向相反的旋轉磁場，磁場同時作用于轉子，轉矩相互抵消[4,16]。由于汽車充電過程和驅動過程不會同時存在，因此，車輛行駛前卸下外接的三相電源后，系統可工作在驅動模式下，控制系統將接觸器S1～S4閉合，電池的直流電經九開關變換器轉化為交流電，驅動電機轉動。本文驅動過程不予討論。

圖1 車載充電器拓撲結構圖

系統工作在充電模式下，將對稱/非對稱六相永磁同步電機(以下簡稱PMSM)進行Clarke變換[4,17]，機電能量轉換平面(α-β平面)中電流分量如表1所示。對于對稱六相PMSM，電流分量為iα=iβ=0，則不存在機電能量轉換。對于非對稱六相PMSM，其電流分量iα、iβ的數值大小成比例(iα/iβ≈3.73)，相位相同，產生脈動磁場，這種磁場也不能使電機轉子轉動。即兩種電機都可以在充電過程中保持轉子靜止，定子作濾波電感，本文采用對稱六相PMSM。

表1

本文重點研究AC-DC整流過程，有關 DC-DC二級變換器和蓄電池模型暫不考慮，并用電阻代替。

1.2 充電模式下電路圖的等效簡化

經過分析計算，在充電模式下，通過調整六相PMSM與三相電源連接順序，定子無法產生旋轉磁場使轉子轉動，定子繞組可充當濾波元件，九開關變換器的中間三個開關始終處于導通狀態。因此，圖1拓撲結構可以等效為如圖2所示的電路圖。圖2中，每兩相繞組并聯，每相定子繞組的電阻、電感相等，進一步可將圖2中三條支路中并聯的電阻、電感值整體等效為R、L。

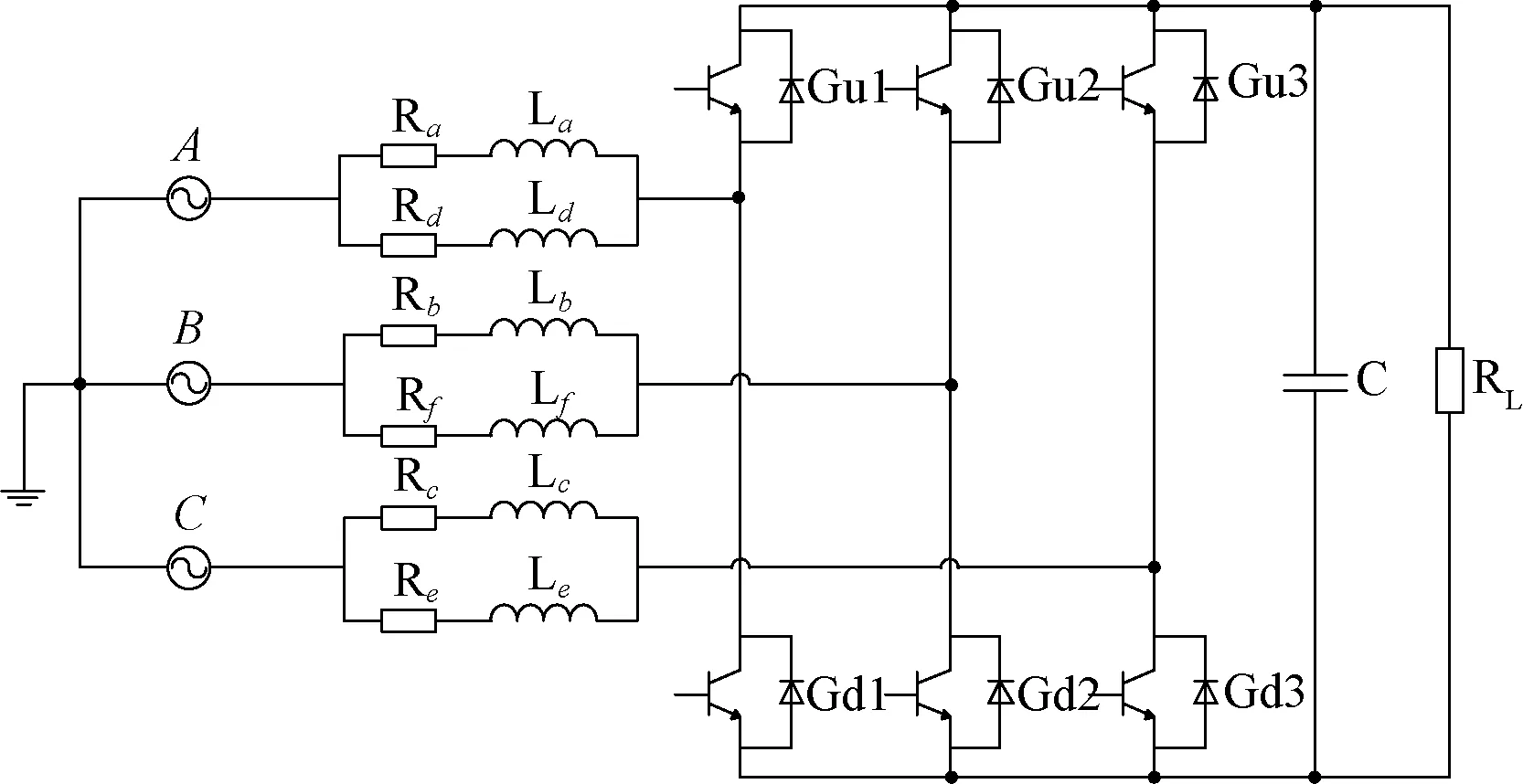
圖2 充電模式下拓撲結構簡化圖

2 雙環滑模變結構控制策略

對于本文的車載充電器模型，設計控制策略有兩個目標：一是當系統運行在充電模式下，輸出直流電壓能快速穩定地跟蹤給定電壓值，并在系統參數發生變化時，有良好的抗擾能力；二是系統能夠工作在單位功率因數下，諧波較小，減少對三相電網的污染，同時減少電機的機械振動。

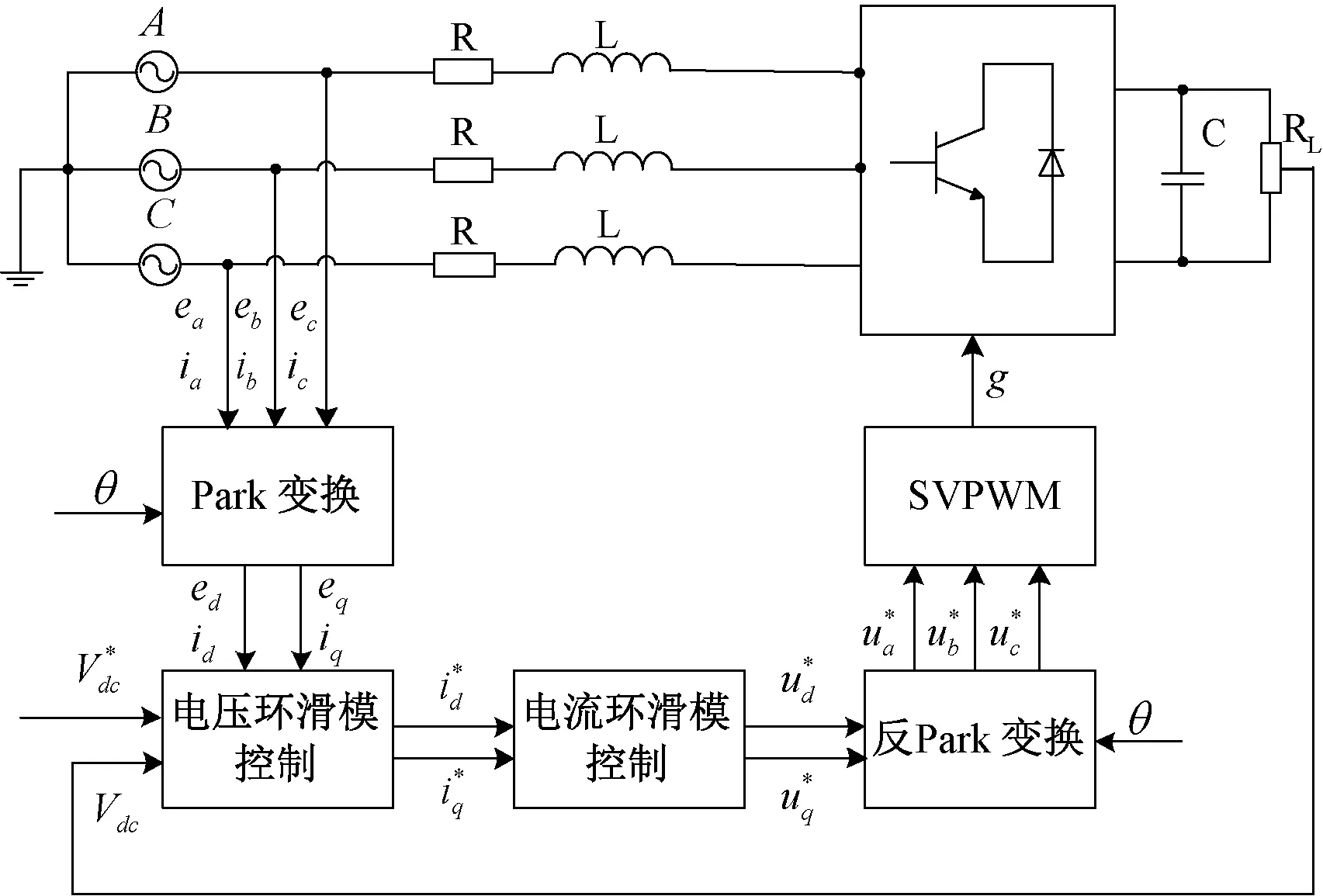
圖3 雙環滑模控制結構圖

2.1 電壓環滑模控制設計

根據等效電路圖，對于交流側，根據基爾霍夫電壓定律可得到系統在三相靜止坐標系下的數學模型：

(1)

對于直流側，根據基爾霍夫電流定律可知：

(2)

根據直流側與交流側的功率平衡關系，可知：

udid+uqiq=idcVdc

(3)

式(3)中,ud、uq、id、iq為d-q旋轉坐標系下的電壓電流分量，iC為流過電容的電流，iR為流過負載RL的電流，Vdc為直流側電壓。將式(2)代入式(3)：

(4)

通過控制交流側電流，達到控制直流側電壓的目的，因此采用積分趨近律設計電壓環滑模面：

(5)

則對式(5)求導得：

(6)

將式(4)代入，可得：

(7)

設計電壓環虛擬控制id的期望值：

(8)

式中：ρu>0。

考慮Lyapunov函數：

(9)

則：

(10)

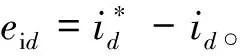
2.2 電流環滑模控制設計

在d-q旋轉坐標系下，式(1)可寫成：

(11)

式(11)寫成矩陣形式：

(12)

通過控制交流側電壓，達到控制交流側電流的目的，同樣采用積分趨近律設計電流環滑模面：

(13)

對式(13)求導，得：

(14)

同理，設計電流環虛擬控制量ud、uq的期望值：

(15)

關于Lyapunov穩定性的證明與電壓環類似，不再贅述。

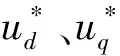
3 仿真驗證

3.1 系統參數配置

為驗證本文控制策略的可行性和有效性，并與傳統PI控制策略對比，分析兩種控制策略的優缺點，將兩種控制策略同時作用于系統，系統參數如表2所示。

表2 系統參數

在控制策略參數設置中，電流環的動態性能影響電壓環的穩定性，進而會影響到整個車載充電器閉環控制系統的穩定性。為了實現收斂速度快的電流環滑模控制，在仿真過程中采用電流環收斂速度大于電壓環的收斂速度，從而保證整個系統的穩定性。本仿真中取：k1=170，kd=kq=1 500，ρu=ρd=ρq=1。

3.2 仿真環境搭建

利用MATLAB/Simulink搭建集成車載充電器控制系統結構圖，如圖4所示。

圖4 系統仿真結構圖

電壓環滑模控制模塊按式(8)搭建，仿真圖如圖5所示。電流環滑模控制模塊按式(15)搭建，仿真圖如圖6所示。有關六相電機的模擬仿真詳見文獻[18-19]。

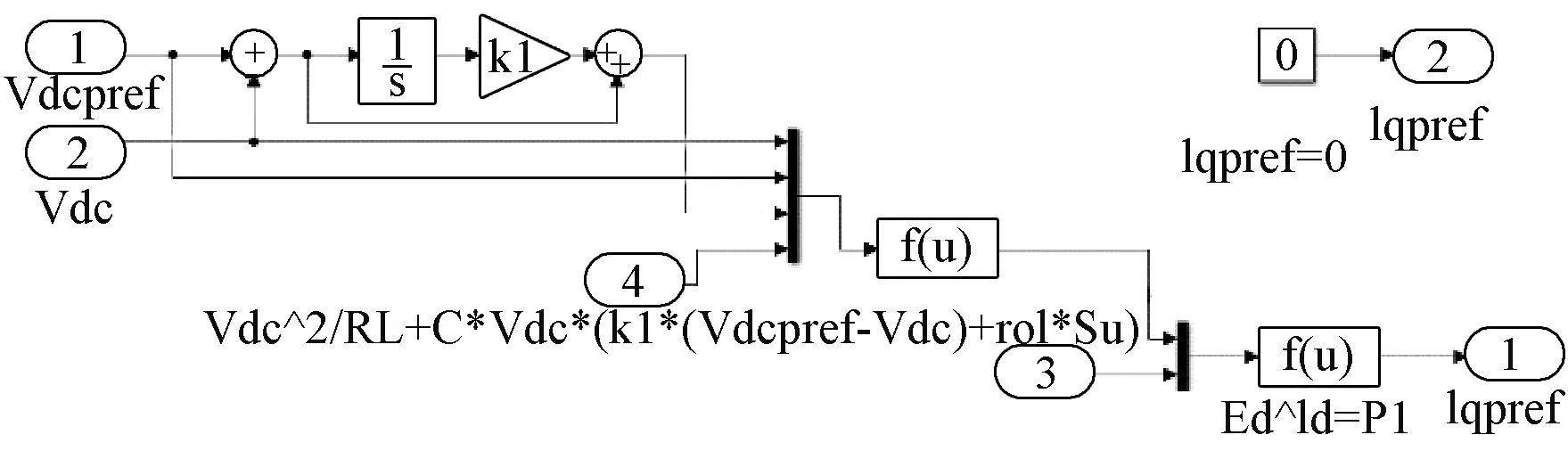
圖5 電壓環滑模控制模塊

圖6 電流環滑模控制模塊

3.3 仿真結果分析

設置初始給定直流輸出電壓為700 V，在0.1 s后，給定直流輸出電壓設置為800 V，兩種控制策略的響應曲線如圖7所示。

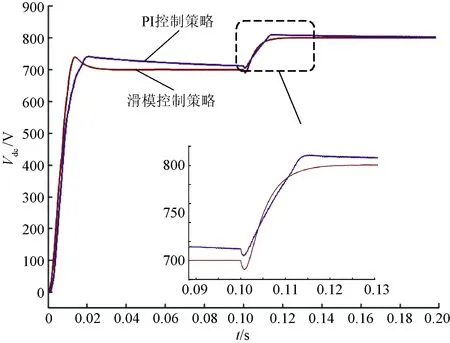
圖7 給定直流電壓變化時，輸出直流電壓對比

在起動階段，滑模控制策略都能使系統在0.03 s內將輸出直流電壓穩定在700 V，而PI控制策略在0.03 s時，直流輸出電壓Vdc≈735 V，隨后誤差緩慢減小，到t=0.1 s時，直流輸出電壓Vdc≈713 V 。

當給定直流電壓發生跳變時，滑模控制策略能在0.02 s內，將直流輸出電壓平滑地升至800 V。PI控制策略過渡時間較長，過渡到穩態后誤差逐漸減小，電壓最終穩定在Vdc≈804 V。

3.3.2 直流側負載電阻RL變化的情況

設置初始負載電阻RL=40 Ω，0.1 s后設置RL=20 Ω，在不改變任何控制參數的條件下，兩種控制策略的響應曲線如圖8所示。

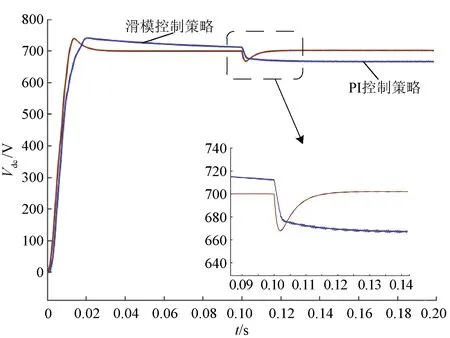
圖8 直流側負載電阻變化時，輸出直流電壓對比

滑模控制策略的輸出直流電壓經過平穩過渡后，在t=0.12 s后能夠穩定在給定電壓700 V；而PI控制策略的直流電壓在t=0.14 s以后穩定在668 V，穩態誤差為32 V。可見，在控制參數不變的情況下，PI控制策略易受直流側負載的影響，當負載發生變化時，無法較好地跟蹤給定直流電壓。

3.3.3 功率因數及諧波分析

設置給定直流電壓為700 V，分析兩種控制策略運行下系統的功率因數和諧波。

根據圖9可知，兩種控制策略均能在單位功率因數(均大于0.995)下運行，但PI控制策略下功率因數的波動略大于雙滑模控制策略，并且在起動階段，滑模控制策略的功率因數(cosφ>0.73)大于PI控制策略下功率因數(cosφ>0.52)。圖10為兩種控制策略下A相電流諧波含量分析圖。其中滑模控制策略下A相電流總諧波畸變率THD=0.84%，PI控制策略下的A相電流總諧波畸變率THD=4.00%。

圖9 兩種控制策略下系統的功率因數

圖10 諧波分析圖

通過仿真結果的分析可見，對比傳統PI控制策略，采用積分趨近律的雙閉環滑模控制策略對給定電壓和直流側負載的擾動具有更好的魯棒性，動態性能更優，并實現了網側電流單位功率因數控制，使得交流側電流的總諧波畸變率更小，對三相電網的污染更少。

4 結 語

本文以集成雙三相PMSM和九開關變換器的車載充電器模型為研究對象，運用滑模變結構控制及SVPWM技術，采用積分趨近律設計充電模式下電壓電流雙環滑模控制策略。通過仿真實驗驗證，與傳統的雙閉環PI控制策略對比，在保證單位功率因數運行和電機不轉動的前提下，當系統參數發生變化時，雙環滑模控制策略擁有更優抗干擾能力和動態性能。