次級結構對直線感應電機運行特性的影響

葛研軍，任廣巍，王大明，劉佳男，周 哲

(大連交通大學 電氣工程信息學院，大連 116028)

0 引 言

直線電動機具有非黏著驅動、結構簡單與性能可靠等特點，是磁懸浮列車和新型非黏著城軌車輛的核心裝備。其中，直線感應電機(以下簡稱LIM)具有結構簡單、可靠性高、散熱性好且無需中間傳動裝置就可實現直線運動等特點，被廣泛應用于城市軌道交通運輸系統和中低速磁懸浮列車中。尤其是對于無法使用現有旋轉電機驅動的磁懸浮列車而言，采用直線電動機驅動具有唯一性和不可替代性[1-2]。

目前，LIM及其次級板結構已成為研究的熱點。韓國漢陽大學的Sung Gu Lee采用3D有限元法分析了懸垂、半帽及全帽型3組次級結構的渦流分布及橫向邊端效應，認為半帽及全帽型結構在合適的寬度下，減小橫向邊端效應影響的效果較好[3]。北京交通大學的張賢設計并對比了兩類籠型LIM的次級模型，通過對比平板型和籠型LIM的次級渦流分布和橫向氣隙磁場分布，得出籠型次級結構在有效區域內可有效減小縱向電流分量，從而削弱橫向邊端效應[4]。北京交通大學的朱金凱通過有限元軟件建模，分析了不同槽距的次級對LIM運行特性的影響，優化出初級齒槽和次級齒槽間的匹配關系，從而提升了直線電動機的推力[5]。

上述文獻僅對LIM次級結構、初級和次級的槽數匹配關系進行了分析和優化，以提升直線電動機的推力，但未分析次級槽型結構對LIM推力的影響。

次級槽型結構對LIM的運行特性、電磁推力、起動和制動響應時間等均起到關鍵性作用。因此，本文提出了一種次級槽結構，該結構不同于現有的LIM次級導體板的槽型，并基于電磁場理論對其電磁推力進行理論建模與分析，然后采用有限元仿真軟件對所建模型進行了驗證。本文還深入分析了趨膚效應對LIM起動性能的影響，并對導體板電流密度對電磁推力的影響進行了研究與探討。

1 LIM運行原理

LIM包括初級結構和次級結構。其中，初級包括鐵心和繞組，次級包括鋁制導體板和鐵背。

與感應型旋轉電機的工作原理相同，LIM通入三相對稱交流電后，會沿其運動方向產生如圖1所示的沿x軸負方向移動的行波正弦磁場。

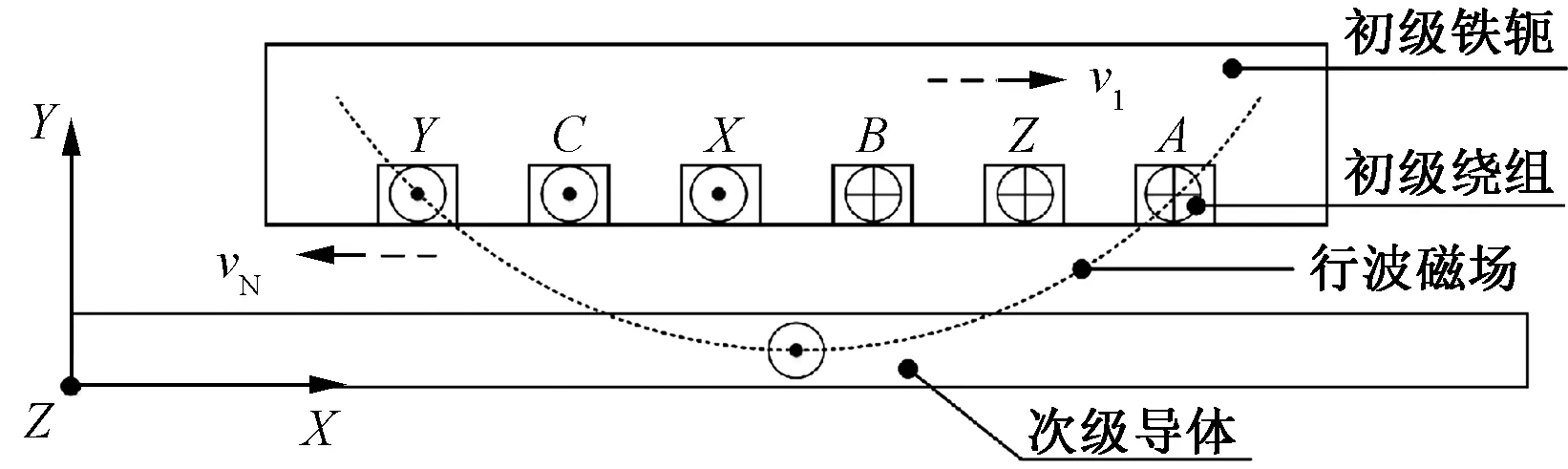
圖1 LIM工作原理

將圖1中的初級結構載流繞組等效為初級結構和氣隙的交界面上均勻等效電流層，且各電場、電流僅沿z方向，則由Maxwell方程可知：

(1)

(2)

式中:H為磁場強度矢量；E為電場強度矢量；D為電位移矢量；B為磁感應強度矢量。

由于電機產生似穩電磁場中，位移電流遠小于傳導電流，即位移電流可以忽略，則式(1)可改寫：

×H=J

(3)

由式(2)及式 (3)可知，z方向電流會在氣隙中產生x、y方向的磁場分量。在y方向的磁場分量和z方向的電流的作用下，LIM產生x方向的電磁推力。

2 直線電動機電流模型

2.1 初級電流分析

設電機初級和氣隙接觸面電流層的電流密度為j1，其幅值為J1，則由文獻[6]可知：

(4)

式中:m1為電機初級相數；N1為每相繞組匝數；I1為初級相電流有效值；Kw1為繞組分布系數；p為極對數；τ為極距。

氣隙磁場由初級電流和次級電流共同產生，設氣隙與次級邊界的電流層電密為j2，當初級和次級間沒有相對位移時，由安培定律可得:

(5)

當導電介質在交變磁場中運行時，將同時出現E和v×B兩種感應電場，因此，式 (5)中的次級電流密度如下:

j2=σ(E+v×B)

(6)

根據磁通連續性定理并綜合式(4)～式 (6)可得:

(7)

式中:μ0為介質磁導率；σ為電導率；δ為氣隙長度。

(8)

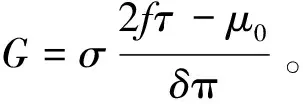
由式(7)及式(8)可知，LIM的氣隙磁場與初級電流幅值成正比，且其場源為初級繞組中所產生的電流。

2.2 次級電流分析

LIM次級導體一般選用鋁或銅等良導體金屬[7]，本文次級導體采用鋁1100。

圖2為工頻條件時，鋁1100的電流密度分布曲線。圖2中，縱軸d為導體表面到導體內部的位置距離，橫軸J為該距離處的電流密度與表面電流密度的比值。

圖2 電流密度分布曲線

由圖2可知，導體截面上，電流密度分布很不均勻，工頻條件下電磁場進入鋁質導體10 mm時的電流密度約為表面的42.8%，進入20 mm時，僅為表面的18.2%。

圖3為矩形導體的LIM在不同導體高度時，LIM達到穩定時所對應的滑差率。由圖3中易得，隨著導體高度的減小，滑差率增大，即穩定時的速度減小。

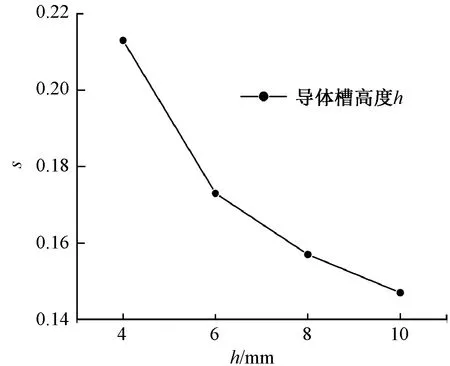
圖3 不同導條高度對穩定運行滑差影響

感應電場由介質表面透入介質中，當其強度衰減到表面強度1/e時，該處到表面的距離稱為趨膚深度。

設趨膚深度為d[8]，則有：

(9)

由式(9)可得，工頻條件下鋁1100的d為11.74 mm。由圖2可知，距離表面越遠，其電流密度的衰減越大。而由圖3可知，減小導體的高度，即可減小在穩定運行時的速度。

因此，鋁制導體的實際深度應略小于趨膚深度，本文定為10 mm。

3 LIM結構參數初設

表1為現有LIM主要參數，圖4及圖5分別為表1參數的LIM結構及機械特性曲線。其中，圖4(a)中為矩形次級導體，h及l分別為次級矩形導體的高度及長度；圖4(b)為LIM的有限元模型。

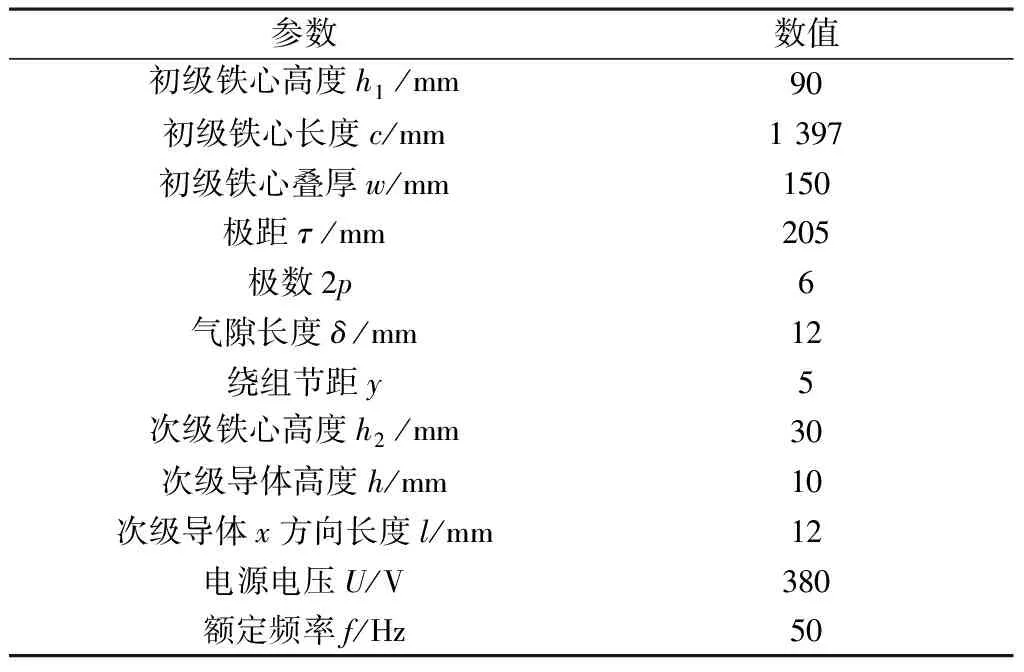
表1 LIM主要參數

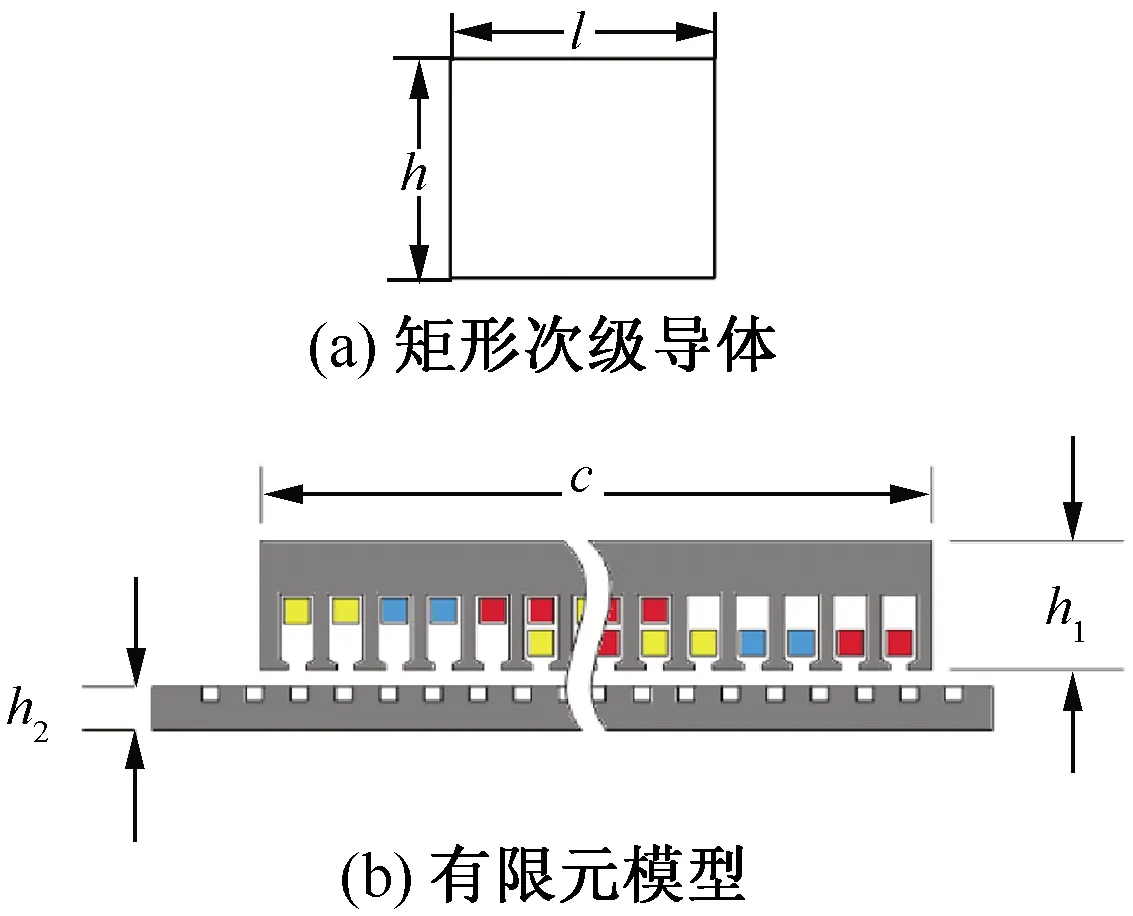
圖4 LIM結構

在Maxwell 2D中設置時，激勵中將次級的鋁制導條進行端部短接，形成籠型次級結構。

如圖5所示，橫坐標s為滑差，縱坐標F為電磁推力，FN為負載，Fs為起動推力。

圖5 機械特性曲線

由圖5可知：接通電源瞬間，LIM初級和次級還未產生相對運動，此時s=1；當LIM的電磁推力F為起動推力Fs，且Fs大于負載FN時，LIM開始起動運行；隨著運行速度的逐漸增大，滑差s隨之減小，F則逐漸增大；當LIM運行速度逐漸接近同步運行速度時，F達到峰值Fmax；此后LIM進入線性運行區間；LIM在線性運行區間內的特征是：隨著運行速度的增大，滑差s將逐漸減小，F將近似呈線性下降，當達到A點時，F=FN，此時LIM進入穩定運行狀態。

4 次級導體結構

選擇次級槽型中導體的結構時，因其與旋轉電機相似，所以考慮窄口槽，如圖6(a)所示。又由于直線電動機的次級較旋轉電機中的長度短，直線電動機次級的鋪設距離較長，若按旋轉電機的模型，則其制作難度較大，所以設計如圖6(b)所示的矩形槽。

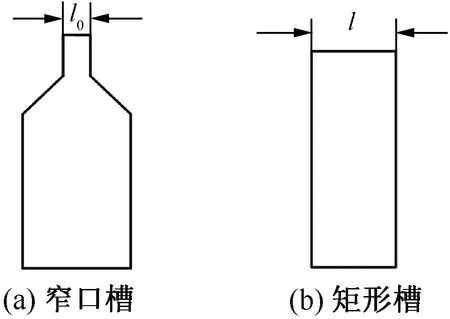
圖6 窄口槽與矩形槽截面圖

窄口槽與矩形槽在同一直線電動機中從起動至穩定時的推力曲線，如圖7所示。

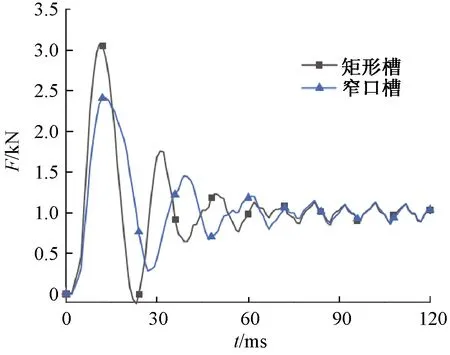
圖7 不同槽口形狀對電磁推力的影響

不同于感應型旋轉電機，氣隙較大的直線電動機中，增大槽口有利于增加峰值推力，且在截面積相同的前提下，穩定運行時的電磁推力沒有明顯變化。同時，由于窄口槽的工藝難度大，直線電動機次級軌道鋪設時難度較大。

因此，在LIM中，籠型次級多選擇矩形槽的結構。

4.1 3種次級導體結構

圖5的次級結構帶載起動時F較小，導致起動及制動時間均較長，尤其制動時所需的安全距離也較長，對列車安全穩定運行有較大影響。

為提高上述狀況的電磁推力，進而提升LIM的起動和制動能力，本文提出了如圖8所示的LIM 2種改進型次級結構。圖8(a)及圖8(b)所示結構的高度與圖4(a)相同，而梯形截面的上邊長及下邊長分別為16 mm和8 mm，三角形截面的底邊為24 mm。

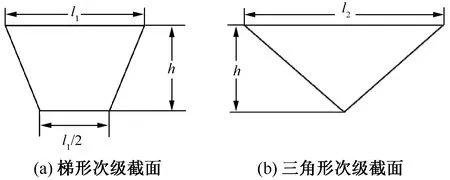
圖8 2種次級導體結構

4.2 對電磁推力的影響

由文獻[9]可得LIM所產生的電磁推力F:

(10)

由式(10)可知，當體積一定時，次級導體所受電磁推力與導體的電流層密度及其在y方向上的氣隙磁密成正比。

為保證圖4(a)、圖8(a)及圖8(b)的次級導體結構在穩定運行時所受的電磁推力相同，應保證3種次級導體結構具有相同的體積，則可得圖8(a)中l1=16 mm，圖8(b)l2=24 mm。

當LIM處于起動和制動狀態時，次級導體中電流分布于表面，導致矩形次級結構的有效載流體積最小，三角形次級結構最大，而梯形次級結構則介于兩者之間。由式(10)可知，矩形次級結構所受的電磁推力F最小，三角形次級結構最大，而梯形次級結構介于兩者之間。

圖9為上述三種結構的電流密度分布情況。

圖9 不同次級結構中的電流分布

由圖9可知，三種導體結構中電流密度分層明顯，證明了本文提出的三角形與梯形結構可在總體積保持不變的條件下，通過增加導體表層體積來提高起動及制動時的電磁推力。

5 運行分析

5.1 不同次級結構機械特性曲線

在380 V電壓源供電時，若設負載為2 000 N，可得不同次級結構的LIM機械特性曲線，如圖10所示。

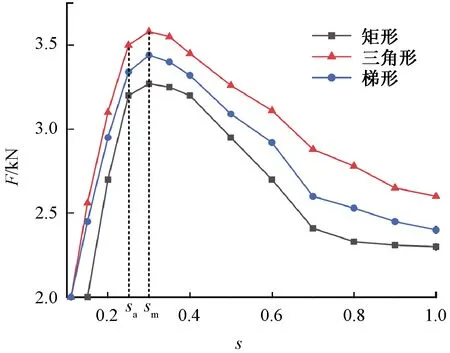
圖10 滑差與電磁推力曲線

由圖10可知，三角形結構的起動推力為2 654 N，矩形結構為2 306 N，梯形導體為2 426 N，三角形結構的起動推力較矩形導體提高15%，而梯形結構則提高了5%。

LIM起動后，隨著轉速逐漸提升，滑差隨之減小，次級導體中仍是三角形的電流密度最大，而矩形結構最小；當滑差達到sm時，電磁推力達到峰值，此時三種結構的電磁推力均達到最大值，其中，矩形導體為3 273 N，三角形導體為3 584 N，梯形導體為3 445 N，三角形導體較矩形導體的電磁推力提高了9%，梯形導體較矩形導體提高了5%。

當滑差s=0.25即達到sa時，LIM進入滑差隨負載變化的近似線性運行階段，該階段中各次級結構特性相差不大。

由式(10)可知，LIM中電磁場源為初級電流，因此可通過計算電磁推力與初級電流有效值的比值，得到如表2所示的單位電流的電磁推力對比。

表2為s=0.9和s=0.3時，不同次級結構單位電流所能提供的電磁推力。

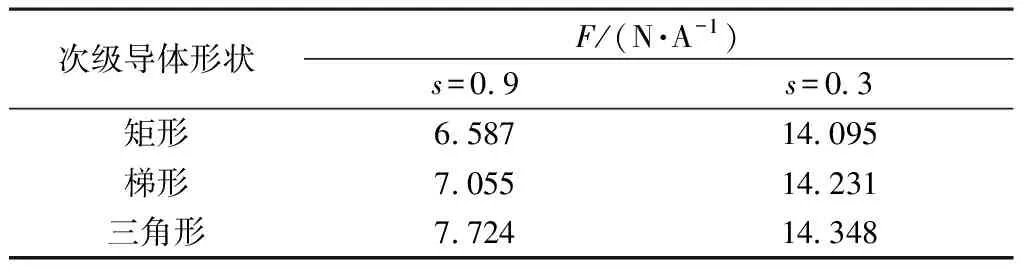
表2 s為0.9和0.3時單位電流電磁推力對比

由表2可得，三角形導體結構單位電流所能提供的電磁推力最大，梯形導體次之，而矩形導體最小。

LIM在實際運行中存在邊端效應的影響[10]，因此，建立三維LIM模型驗證上述結論在考慮邊端效應時的適用性。設次級導體板z方向的寬度為a：

a=w+2×τ/π

(11)

計算得到次級導體板的寬度為280 mm，考慮加工中的工藝精度，次級導體板的寬度取430 mm。

三維模型不同于二維模型，在二維模型中未考慮初級繞組端部連接處的漏感的變化，導致二維模型有一定誤差，因此建立三維模型對二維模型進行驗證。

三維有限元模型如圖11所示，得到不同次級結構的機械特性曲線，如圖12所示。

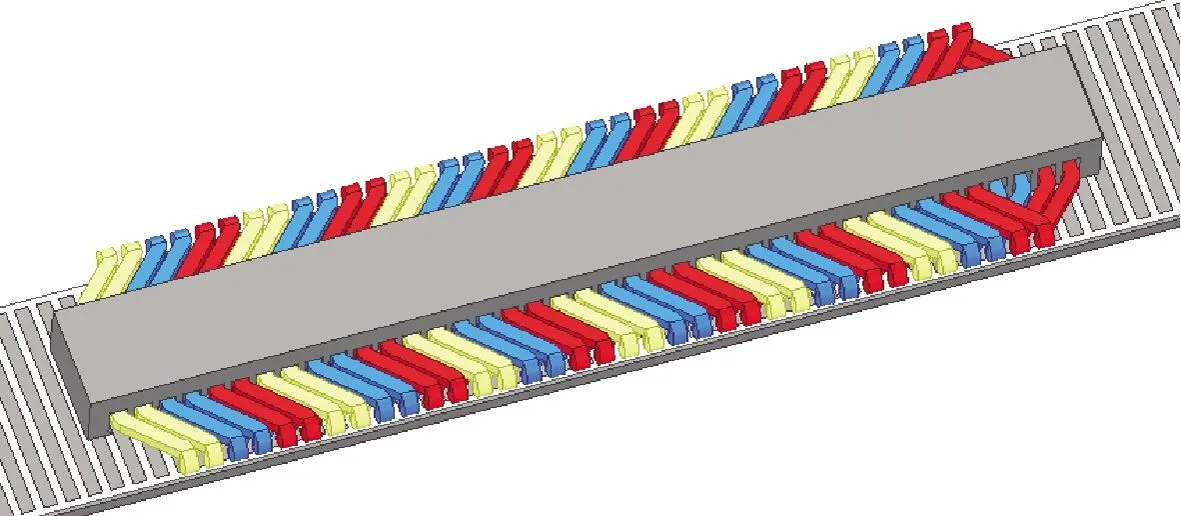
圖11 LIM三維有限元模型

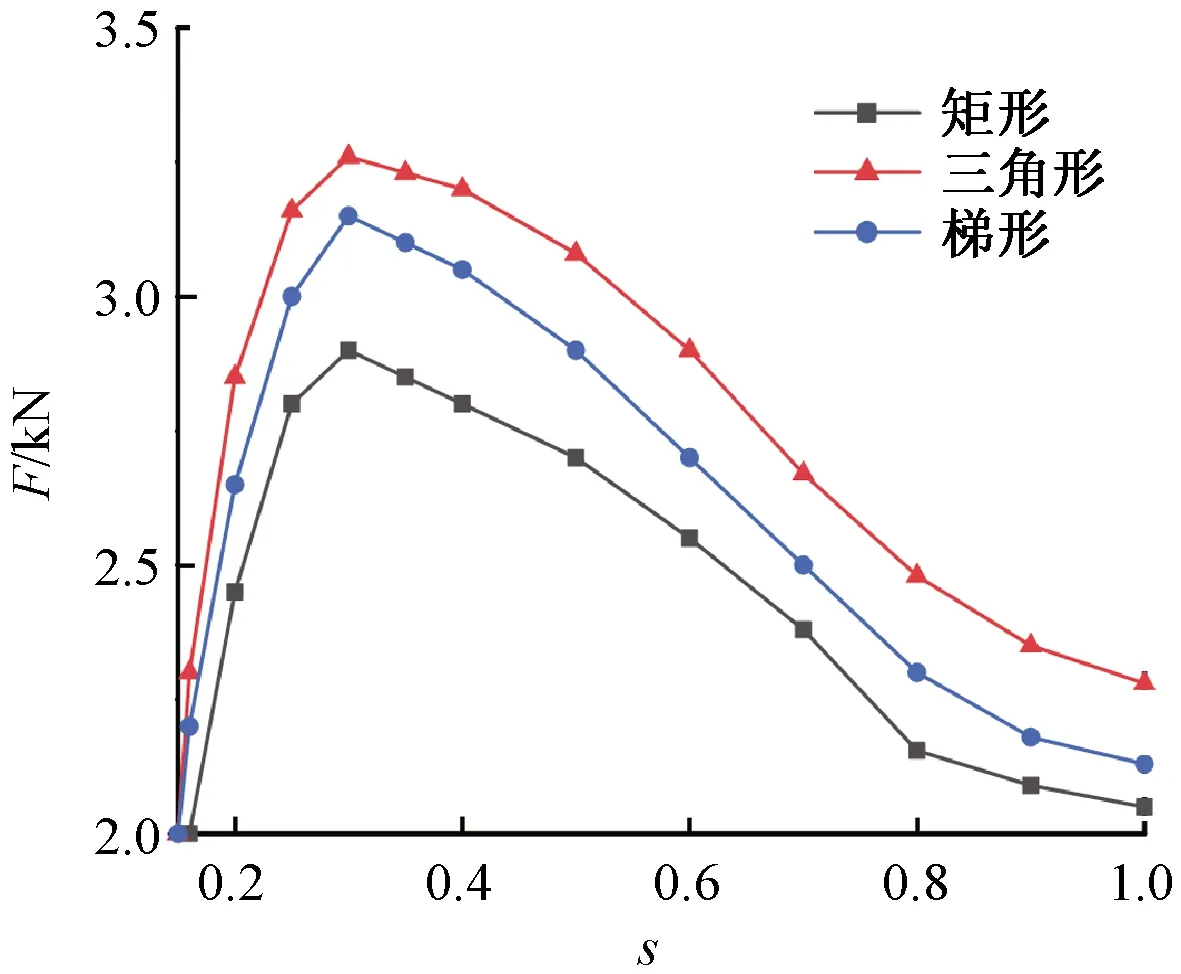
圖12 三維各次級滑差與電磁推力曲線

由圖12可知，起動時三角形導體所能提供的電磁推力最大，矩形結構最小，而梯形結構則介于兩者之間。其中，三角形結構的起動推力為2 284 N，矩形結構為2 056 N，梯形導體為2 134 N，三角形結構的起動推力較矩形導體提高了11%，而梯形結構則提高了3.8%。

當電磁推力達到峰值，此時矩形導體為2 956 N，三角形導體為3 265 N，梯形導體為3 158 N，三角形導體較矩形導體的電磁推力提高了10%，梯形導體較矩形導體提高了6.8%。

由此亦證明了改變次級導體結構能夠提升電流密度，改進后三角形導體結構能提供更高的電磁推力，而梯形導體結構稍遜于三角形導體結構。

5.2 制動運行

制動運行是指LIM運行在電氣制動的反接制動狀態[11]。

圖13為LIM運行至250 ms時將其進入反接制動狀態時的運行曲線。實際制動時間=總時間-穩定運行時間。

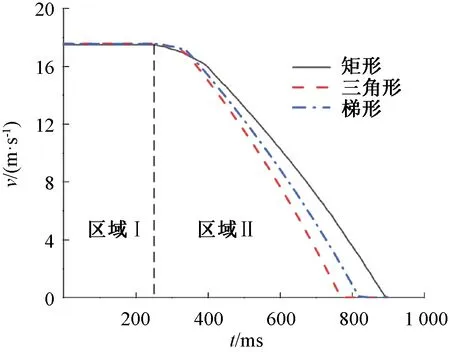
圖13 不同次級結構制動運行曲線

由圖13可知，矩形導體、三角形導體和梯形導體的制動時間分別為650 ms、520 ms和570 ms。若以矩形導體制動時間為基值，并將其制動時間設為1，則梯形導體的制動時間為0.87，三角形為0.8，即梯形導體的制動時間較矩形導體減少了13%，三角形則減少了20%，說明三角形導體的制動效果最優。

設LIM的總質量為40 kg，矩形導體結構的制動所需的時間為1，并以質量的0.1倍為變化量，按上述方法可得各次級導體結構隨質量變化時所需制動時間的分布圖，如圖14所示。

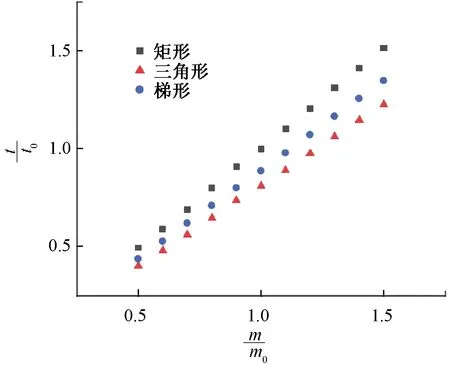
圖14 質量-制動響應時間

由圖14可知，LIM制動時，當質量比由0.5增加至1.5時，制動響應時間也相應增加，質量為初始的0.5時，所需的制動時間相對較小，梯形導體及三角形導體分別減少了10%及15%；隨著質量倍數的增加，梯形和三角形導體所需的制動時間也明顯縮短，當質量為1.5倍時，梯形導體和三角形導體的制動時間分別較矩形導體縮短了20%和30%。

由上述分析可知，三角形導體和梯形導體均能夠減少制動響應時間與制動距離，且三角形導體的制動時間與制動距離均優于梯形及矩形導體結構。

綜上，通過對LIM電流模型的分析與研究，提出的三角形及梯形兩種次級導體結構，在總體積及穩定運行時電磁推力不變的條件下，三角形的起動推力最大，所需要的制動時間最短，因此本文選用三角形結構作為最優的改進籠型次級導體結構。

6 結 語

針對現有LIM次級導體矩形結構的起動推力小、制動時間長等缺陷，提出了兩種改進型次級導體結構，在對其進行深入分析基礎上，得到如下結論：

(1)LIM矩形次級導體結構在12 mm氣隙條件下所產生的電磁推力較小，且制動過程較長，存在一定的安全隱患。

(2)三角形及梯形兩種次級導體結構，在總體積與矩形結構相等的條件下，通過有限元仿真得到了不同次級結構的機械特性曲線。

(3)通過分析三種結構的特性曲線及單位電流所產生的電磁推力，驗證了三角形結構的電磁推力最大，所需要的制動時間最短。

(4)LIM制動時間與其質量呈正相關性，質量越大，所需的制動時間越長。