圓柱型粗糙元誘導的超聲速邊界層轉捩實驗研究

金 龍，易仕和，霍俊杰，劉小林，牛海波

(國防科技大學 空天科學學院，長沙 410073)

邊界層轉捩是由自由來流或者物體本身的擾動引起的，這些擾動通過邊界層感受性機制傳入邊界層，并以各種不穩定模式增長，最終引起湍流[1].在超聲速來流中，邊界層轉捩受諸多因素的影響，轉捩位置難以被預測[2-3].粗糙元已經被證實是控制邊界層轉捩和分離特性的有效方法，例如在超燃沖壓發動機的啟動和燃料摻混中有重要應用[4].粗糙元有多種不同形式，大致可以分為二維粗糙元、孤立粗糙元和分布式粗糙元.大多數情況下，粗糙元會影響邊界層的轉捩位置，隨著粗糙元高度的增加，轉捩位置會向粗糙元靠近.

自20世紀60年代開始，粗糙元誘導邊界層轉捩問題開始受到廣泛關注，各國學者針對超聲速突起物繞流做了大量的研究工作，文獻[5]系統地總結了前人在粗糙元對高超聲速邊界層轉捩的影響方面所做的工作.在超聲速和高超聲速邊界層中，三維粗糙元可以通過多種方式影響層流邊界層轉捩，這取決于粗糙元的尺寸、形狀和粗糙元之間的相對位置.文獻[6]研究發現，在同一來流條件下，當粗糙元的高度超過某一臨界值時，隨粗糙元高度的增加轉捩位置向上游移動，直到接近粗糙元并轉變為強迫轉捩.文獻[7]通過實驗研究了不同高度的方型粗糙元對邊界層轉捩的影響，發現方型粗糙元的臨界高度為0.15，而當臨界高度大于0.32時，則會繞過較為溫和的轉捩過程，產生完全湍流的尾流.文獻[8]研究了不同高度圓臺繞流的流場結構，發現不同高度圓臺的三維弓形脫體激波的后掠斜坡角度基本相同，圓臺高度對于尾跡區影響顯著，高度較低時層流區和轉捩區相對較長.文獻[9]在普渡大學的靜風洞中進行了馬赫數為6.0圓柱繞流實驗研究,發現在圓柱尺寸較大時對于邊界層的擾動是絕對的；當圓柱尺寸較小時，擾動則是對流的，即產生的擾動較小，會在向下游傳播的過程中不斷發展.文獻[10]針對半球形粗糙元進行的油流實驗顯示，在相鄰粗糙元中心距小于4倍粗糙元的展向最大寬度時，渦流間的相互作用會降低粗糙元對邊界層影響的效能.

近年來，高精度計算的蓬勃發展為精確地描述粗糙元誘導邊界層轉捩的物理機理提供了基礎.文獻[11]采用5階精度加權緊致非線性格式(WCNS-E-5)，對不同高度條件下的圓柱粗糙元下游流動結構進行研究，結果與文獻[8]所做工作高度吻合.文獻[12]采用直接數值模擬(DNS)和油膜干涉(OFI)技術相結合的方法，研究平板邊界層在帶粗糙元和不帶粗糙元條件下的流場.結果表明，相鄰兩個粗糙元之間的相互作用可以觸發剪切層的失穩，同時也可以抑制邊界層的轉捩和馬蹄渦的發展.本文中的“馬蹄渦”是指由于來流繞過圓柱而產生的存在于圓柱周圍的渦結構，而非“發卡渦”的別稱.

眾多研究表明，控制邊界層轉捩及分離特征，粗糙元是一種有效途徑.但是目前的研究多側重于單個粗糙元的轉捩機理，對于多個粗糙元相互作用的轉捩機理還缺乏成熟的結論.本文的研究目的在于研究多個粗糙元相互作用對于邊界層的影響規律.首先，介紹了相關的實驗設備及測試技術；然后，獲得了單個和多個粗糙元誘導的邊界層流向和展向流場結構，并分析粗糙元間相互作用對于邊界層中擬序結構的影響；最后，利用分形理論對邊界層轉捩的納米粒子示蹤的平面激光散射(NPLS)技術圖像進行了定量分析，獲得邊界層轉捩位置，借助轉捩位置對單個粗糙元和多粗糙元對邊界層轉捩的影響進行了分析.本文中對粗糙元誘導的邊界層流場精細結構和轉捩特點進行分析，為粗糙元控制邊界層轉捩機理的研究提供了實驗支撐.

1 實驗設備及相關測試技術

1.1 超聲速風洞和平板模型

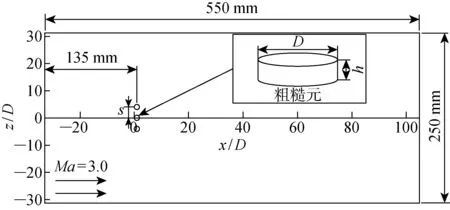
圖1 實驗模型示意圖Fig.1 Schematic diagram of experimental model

所涉及的超聲速實驗依托國防科技大學空氣動力學實驗室的KD-03直連式超聲速風洞.該風洞的運行方式為吸氣式，來流總壓p0=0.1 MPa，總溫度T0=300 K，單位雷諾數為Re=7.49×106m-1，所涉及的相關實驗研究的風洞運行馬赫數為Ma=3.0.實驗模型如圖1所示，其中：x為流向坐標軸；z為展向坐標軸；D為粗糙元直徑；h為粗糙元高度；s為相鄰粗糙元間的距離.實驗模型是長為550 mm、寬為250 mm、厚為13 mm的平板，材質為碳鋼，平板模型的攻角α=0°.實驗過程中，平板壁面溫度基本不變，可以看作是等溫壁.粗糙元的前緣為坐標原點建立的坐標系，利用粗糙元的直徑對坐標進行歸一化處理.圓柱型粗糙元分為A型(D=4 mm，h=1 mm)和B型(D=4 mm，h=0.5 mm)兩種.粗糙元的安裝位置選擇距離平板前緣135 mm處，此處的邊界層厚度與粗糙元的高度在一個數量級上.對于多個粗糙元相互影響的實驗，取s=2D.在此情況下，粗糙元對于邊界層轉捩的影響將更易被觀測.

1.2 納米粒子示蹤的平面激光散射技術

所采用的NPLS技術是所在研究小組自主研發的以現代激光、成像、圖像處理技術為基礎的高時空分辨率測量技術[13].NPLS技術已經被證實在超/高超聲速流動測量實驗中具有較高的流動成像信噪比[14-16].系統采用Nd:YAG雙腔激光器，輸出波長為532 nm，脈沖激光強度為350 mJ，脈寬為6 ns.跨幀電荷耦合器件(CCD)相機分辨率為 2 048 像素×2 048 像素，灰度等級為 4 096 級，采用的拍攝頻率為5 Hz，兩幀時間相關圖像之間的時間間隔設置為0.2 μs，CCD相機和激光器由同步控制器發出信號進行控制.NPLS系統示意圖如圖2所示.

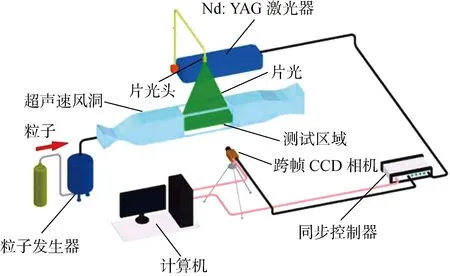
圖2 NPLS系統示意圖Fig.2 Schematic diagram of NPLS system

2 實驗結果及分析

2.1 平板超聲速邊界層流場

圖3 局部放大的平板邊界層流向NPLS圖像Fig.3 Typical streamwise NPLS images of boundary layer with its partial enlarged view

當馬赫數為3.0時，平板邊界層瞬時NPLS圖如圖3所示，其中：y為距離平板表面的高度.由圖3可知，在突起物安裝位置附近，邊界層非常穩定并保持層流狀態,沒有任何轉捩和失穩跡象.根據NPLS技術測量結果的圖像灰度與流場密度間的關系，定性認為壁面附近的低灰度區域為邊界層.由圖3(a)可知，隨著邊界層的發展，其厚度逐漸增加，經測量得到x/D=0處的邊界層厚度δ=0.9 mm，其由NPLS圖像計算獲得.邊界層繼續發展，出現了邊界層擬序結構，圖3(b)中的渦結構是典型的發卡渦結構.在x/D=25處，平板邊界層仍然未轉捩為完全湍流.目前，對于邊界層轉捩位置的判斷國內外尚無統一的標準，故重點關注邊界層轉捩為完全湍流的位置，即大尺度渦結構消失破碎為不規則的小尺度渦結構處，下文提到的轉捩位置即指該位置.

圖4 單個A型粗糙元尾跡邊界層的典型NPLS結果Fig.4 Typical NPLS results of boundary layer transition induced by single type A

2.2 單個粗糙元誘導的邊界層轉捩

單個A型粗糙元尾跡邊界層流場的瞬態和平均NPLS圖如圖4所示.其中：yA為單個A型粗糙元的片光高度；hA為A型粗糙元高度；灰色區域為平板壁面和粗糙元的截面部分.由圖4可知，包括弓形激波、膨脹波和再附激波在內的超聲速流動的精細結構，且可以觀察到粗糙元尾跡邊界層的發展過程.由圖4(a)可知，在x/D=4處均出現了具有較強規律性的大尺度渦結構，這是存在于粗糙元尾跡中的發卡渦的頭部流向結構，和自然轉捩的邊界層有所不同.由A型粗糙元誘導的邊界層中出現的發卡渦結構相較于文獻[17]提出的“發卡渦包”結構排列更為緊密.隨著邊界層的發展，大尺度渦結構會破碎成小尺度渦結構，當大尺度渦結構完全破碎為小尺度渦結構時,即為完全湍流.由圖4(c)可知，在x/D=3附近可以觀測到發卡渦“頸部”結構的出現.理想化發卡渦是一種三維結構，由一對對稱旋轉的準流向渦構成腿部結構，兩條腿通過頸部，最后連接在頭部，如圖5所示.其中：U∞為來流速度；ωx、ωz分別為沿x、z方向的渦量.由于主流相對向下的運動速度與發卡渦誘導向上的運動速度會在空間某一位置達到平衡(即相對運動速度為0)，形成斜剪切層結構，發卡渦整體具有斜向上傾斜的趨勢.由于發卡渦結構具有傾斜結構，所以圖4(c)中觀測到的發卡渦“頸部”結構的位置相較于圖4(a)中發卡渦“頭部”結構的位置更靠近上游.

圖5 理想化的發卡渦示意圖Fig.5 Schematic diagram of idealized hairpin vortex

圖6 單個B型粗糙元尾跡邊界層的典型NPLS結果Fig.6 Typical NPLS results of boundary layer transition induced by single type B

單個B型粗糙元尾跡邊界層流場的瞬態和平均NPLS圖如圖6所示.其中：yB為單個B型粗糙元的片光高度；hB為B型粗糙元高度.由圖6可知，弓形激波和再附激波強度相比于圖4中的強度都較弱.在邊界層轉捩為完全湍流之前也存在大尺度渦結構.然而與圖4中的大尺度渦結構相比，其規律性不強，更接近于無附加擾動的邊界層轉捩.由圖6(c)可知，無法清晰地分辨出發卡渦的二維結構，在此片光高度內，流動主要處于邊界層的內部，此時發卡渦的二維結構呈現出“條帶狀”，而白色的條帶狀結構是位于發卡渦腿部渦管軸線外側的流動.兩種情況下，粗糙元誘導的邊界層都在一定距離內保持穩定狀態后失穩，這說明與邊界層厚度相近的粗糙元對于邊界層的控制是有效且相對穩定的，流場不會立刻出現大的脈動結構.

2.3 多粗糙元相互影響的邊界層轉捩

為了更加直觀地觀測粗糙元之間的相互作用，展示粗糙元尾跡邊界層的展向結構，粗糙元尾跡邊界層轉捩的典型展向NPLS結果如圖7所示.由圖7可知，粗糙元尾跡邊界層逐漸失穩，最終轉捩為完全湍流的過程.考慮不同粗糙元高度會導致粗糙元后邊界層厚度不同，A型和B型粗糙元的片光高度分別取：yA/hA=1和yB/hB=1.由圖7(a)和7(b)可以發現，中間粗糙元的尾跡轉捩區較長(由NPLS圖像判斷，轉捩位置約為x/D=10)，而兩側粗糙元尾跡轉捩為完全湍流的位置更靠近上游(由NPLS圖像判斷，轉捩位置約為x/D=8).而圖7(c)和7(d)在一定程度上與圖7(a)和7(b)有相似之處，處于中間位置的粗糙元尾跡邊界層轉捩位置約為x/D=20(由NPLS圖像判斷)，而兩側粗糙元尾跡邊界層轉捩位置約為x/D=15.這反映出中間粗糙元尾跡邊界層轉捩受到了一定程度的抑制.

圖7 多粗糙元尾跡邊界層轉捩的典型展向NPLS結果Fig.7 Typical spanwise NPLS results of boundary layer transition induced by multiple roughness element wakes

仔細觀察圖7(a)和7(c)發現，兩側粗糙元尾跡中存在明顯的發卡渦“頸部”和“腿部”結構，但在中間粗糙元尾跡中發卡渦結構難以被觀測到.這表明中間位置粗糙元尾跡中的發卡渦結構演化也受到一定程度的抑制.而文獻[12]通過分析DNS和OFI結果發現，粗糙元周圍生成的馬蹄渦結構的演化也會因為粗糙元間的相互作用而受到抑制.雖然其沒有深究馬蹄渦受到抑制的原因，但本節發現粗糙元尾跡邊界層中的發卡渦同樣也會被抑制.文獻[10]認為粗糙元間的相互作用抑制了下游渦絲的發展.

2.4 基于NPLS圖像的邊界層特性定量分析

邊界層中的擬序結構在具有瞬態空間特性的同時也包含統計特性，合理運用圖像處理技術，可以達到對邊界層擬序結構的統計特性進行定量分析的目的.分形維數是用來描述不規則曲線破碎程度的幾何量.例如：一條直線的分形維數為1，而一個平面的分形維數為2，因此任意一條二維曲線的分形維數在1和2之間.如果分形維數越高，則表示該曲線的破碎程度越高，或者越充滿一個平面空間；而分形維數越低，則代表這條曲線破碎程度越小，或者越接近一條一維直線.對邊界層而言，在其由層流過渡為湍流的過程中伴隨著流動的失穩、大尺度渦結構的出現和破碎以及最后小尺度渦結構的生成，這是一個有序到無序的過程.NPLS圖像反應的是流場的二維特性，當拍攝方向沿流向時，邊界層與主流的分界面在NPLS圖像中反應為一條不規則曲線，理論上可以采用分形維數來描述邊界層的空間結構特性.

分形理論在流體力學領域已經得到了廣泛的應用，目前較為常用的方法為計盒維數法.將邊界層與外部流動之間的邊界作為平面集F進行分形維數研究，為了計算平面集合F的盒維數，可以構造一些邊長為l的正方形(即“盒子”)覆蓋該平面集.平面集F的分形維數可以表示為

(1)

式中：Nl(F)為“盒子”與平面集F的相交數量.

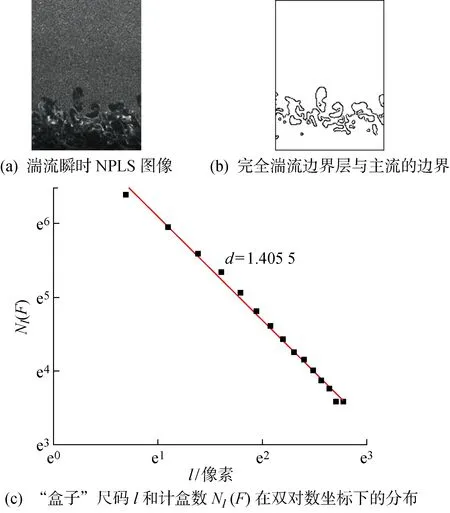
圖8 充分發展的湍流邊界層的分形分析結果Fig.8 Fractal analysis results of fully turbulent boundary layer

充分發展的湍流邊界層的分形分析結果如圖8所示，其中：d為平均分形維數.從圖8(c)中可以看出，l越小，Nl(F)越大.在雙對數坐標系下，“盒子”尺碼l與計盒數Nl(F)可以擬合為一條直線，直線的斜率取負，則對應湍流邊界層的d=1.405 5.

圖9 不同邊界層狀態NPLS圖像分形維數結果Fig.9 Fractal dimension results of NPLS images in different conditions of boundary layer

采用計盒維數法對不同狀態邊界層分形維數的結果如圖9所示.在對NPLS進行分形維數的過程中，先對NPLS圖像進行二值化處理，對得到的二值圖像運用基于Canny方法的邊緣檢測技術提取邊界層和外流場的分界線，最后通過計算得到邊界層的分形維數.在計算邊界層的分形維數時，沿流動方向將測量區域按10 mm長度進行分段，保證分形維數反映的是局部邊界的破碎程度.

圖10 不同狀態分形維數統計結果Fig.10 Statistical results of fractal dimension in different conditions

由于NPLS技術得到的圖像結果是瞬態的，所以需要借助分形理論對結果進行分析，獲得其中的統計特性.本文針對6種不同的實驗狀態(C1～C6)，各選取50張流向NPLS瞬態圖像，分別計算其分形維數后取平均，結果如圖10所示.由圖10(a)可知，C2的上升趨勢明顯滯后于C1.同時，可以觀察到C3的上升趨勢介于這兩者之間，相對更接近C1.由單個A型粗糙元誘導的邊界層轉捩位置為x/D=6;當粗糙元兩側存在A型粗糙元時，轉捩位置推遲至x/D=11;而當兩側存在B型粗糙元時，轉捩位置推遲至x/D=8.5.這意味著兩側存在的A型和B型粗糙元都能夠對中間的A型粗糙元誘導的邊界層轉捩產生抑制作用，C2中的抑制作用要強于C3.由圖10(b)可知，C4和C6的上升趨勢相近，而C5的上升趨勢要滯后于二者.兩邊的B型粗糙元抑制了中間B型粗糙元誘導的邊界層轉捩，轉捩位置從x/D=18.5附近推遲到了x/D=23.5后.但是在C6中，兩側的A型粗糙元對于中間B型粗糙元誘導的邊界層轉捩并沒有明顯的抑制作用.原因可能在于，A型粗糙元產生的擾動更強，其尾跡邊界層中的渦結構更強，而B型粗糙元對邊界層的擾動相對較小，當中間放置B型粗糙元而兩邊放置A型粗糙元時，A型粗糙元誘導的邊界層中的擾動可能會橫向傳播影響，B型粗糙元邊界層的發展，相當于給B型粗糙元尾跡邊界層附加了額外的擾動，導致其更快轉捩，所以在C6中沒有出現粗糙元相互作用導致的邊界層發展抑制現象.由此可以看出，多個粗糙元之間相互作用會削弱其促進邊界層轉捩的有效性，這與NPLS展向觀察結果相吻合.但是如果兩側的粗糙元高度大于中間的粗糙元，對于中間尾跡邊界層的抑制作用可能不明顯.

3 結語

本文采用NPLS技術研究了超聲速平板上圓柱型粗糙元誘導的邊界層轉捩過程，獲得了流向和展向精細的流場結構.x/D=0處未受擾動的層流邊界層厚度δ=0.9 mm，研究采用A型(h=1 mm)和B型(h=0.5 mm)兩種粗糙元.典型的NPLS結果表明，粗糙元誘導的邊界層將在一定距離內保持層流狀態，進而出現一系列有規律的發卡渦結構.展向NPLS結果和邊界層的分形維數表明，多個粗糙元之間的相互作用可以抑制下游邊界層的轉捩.同時，通過NPLS結果直觀地觀察到，粗糙元之間的相互作用對下游的發卡渦發展起抑制作用.A型粗糙元間的相互作用導致邊界層轉捩位置從x/D=6推遲至x/D=11，而對于B型粗糙元，轉捩位置從x/D=18.5附近推遲至x/D=23.5后.但如果兩側的粗糙元擾動過強，擾動可能會傳播至中間粗糙元誘導的邊界層中，導致其提前轉捩.