基于數值實驗的艙外航天服肩法蘭布局優化研究

管鯤甯， 李潭秋， 李道奎， 李元豐

(1.國防科技大學空天科學學院， 長沙 410073； 2.中國航天員科研訓練中心， 北京 100094)

1 引言

航天員著艙外航天服后的活動性是保證航天員順利完成出艙任務的前提，取決于航天服上軀干結構與人體上肢生理參數的符合程度。 上軀干結構對人體上肢運動的影響通過肩法蘭對上肢運動的限制實現。 航天員著艙外航天服時，其雙臂通過上軀干的肩法蘭開口穿入艙外服上肢組件，因此肩法蘭的布局對人體著服后上肢的活動范圍影響至關重要。

NASA 的Z-2 航天服在Z-1 航天服的基礎上進行改進，縮減了左右肩法蘭中心距，并對肩法蘭的空間角度進行了優化[1]。 但該優化需要大量的工程研制經驗作為支撐，時間周期較長；Williams[2]通過人體掃描方法獲得人體上肢在活動過程中與肩法蘭的作用關系，研究表明肩法蘭對人體上肢活動的限制體現在對人體肩部以及上臂的擠壓，會對人體造成傷害，影響上肢活動能力。Heather[3]設計肩法蘭模擬裝置研究肩法蘭布局隨人體上臂活動的變化情況，結果表明肩法蘭布局與人體上肢活動間存在明顯的相互關系，并獲得了肩法蘭位置及空間角度與上肢活動情況的回歸模型。 但上述研究對上肢活動的表達尚不充分，得到的結論無法闡釋肩法蘭對上肢活動性影響的原因。 李元豐等[4－6]根據上軀干結構組成研制了上軀干結構原理樣機，開展了肩法蘭與上肢活動相關性實驗，得到了肩法蘭設計因素與單、雙手操作空間相對體積的關系，但因相關性實驗缺乏對人體肩關節、肘關節的系統分析，且普適性不足，難以覆蓋肩法蘭的所有布局方案。

本文根據人體上肢生理學特點，分析肩法蘭對人體上肢活動的影響方式，在人體上肢可達域運動學模型的基礎上增加肩法蘭約束，建立肩法蘭與人體上肢耦合模型；并針對4 個設計因素(左右肩法蘭中心間距l，肩法蘭內徑d，角度γ以及角度α)，開展數值仿實驗，研究肩法蘭各設計因素對人體上肢活動性的影響，以獲得艙外航天服肩法蘭布局與人體上肢活動的相互作用關系，為肩法蘭布局方案的設計與評價提供參考。

2 艙外航天服肩法蘭與人體上肢耦合模型

2.1 人體上肢可達域運動學模型

依據Klopcar 等[7－8]的研究結果，利用Matlab編程建立1 種3 剛體7 自由度的人體上肢可達域運動學模型，如圖1 所示。 人體坐標系中心定義于內肩關節中心，x軸沿人體冠狀軸方向，y軸沿人體矢狀軸方向，z軸沿人體垂軸方向，則有式(1)所示耦合關系[9－10]:

圖1 上肢可達域運動學模型Fig.1 Kinematics model of upper limb reachable area

式中，φrp、φde表示內肩關節繞x、y軸轉動角度；φA、φF、φR分別代表肩關節外展/ 內收、前屈/后伸以及旋內/ 旋外的活動角度；φEF表示肘關節的屈/伸運動角度；rSG、rH、rF分別表示肩胛帶向量(即內、外肩關節中心距離向量)、上臂向量和前臂向量；rw為腕關節中心位置向量，R代表關節繞相應方向的旋轉矩陣。 在上肢運動過程中，各個關節的活動間存在耦合關系[11－12]。

2.2 肩法蘭與人體上肢耦合模型

肩法蘭對肩關節復合體運動的約束如圖2 所示，紅色圓環表示的肩法蘭對肩關節復合體運動的約束明顯。 當肩法蘭的相對位置位于人體肩寬內部時，對鎖骨的擺動和肩胛骨的滑動范圍進行了約束，因此大大影響了上肢的運動范圍。 肩法蘭對上臂的活動范圍也有限制作用，主要是通過物理碰撞實現。

圖2 肩法蘭對肩關節復合體運動的約束Fig. 2 Constraints of shoulder flange on shoulder joint complex

肩法蘭布局的設計因素包括:左右肩法蘭中心距離l，肩法蘭內徑d，角度γ以及角度α，其中，角度γ和α是肩法蘭的空間角度[13]。 角度γ定義為肩法蘭繞其局部坐標系z軸轉角，角度α為肩法蘭繞局部坐標系y軸轉角，肩法蘭角度定義如圖3 所示。 在模型中，通過調整肩法蘭各個設計因素可實現肩法蘭布局的變換，而肩法蘭布局的設計過程即確定各個設計因素參數的過程。

圖3 肩法蘭角度定義Fig.3 Definition of shoulder flange angle

本文搭建了肩法蘭與人體上肢耦合模型。 首先建立人體上肢可達域運動學模型，然后以人體上肢可達域運動學模型為基礎，對上肢運動施加肩法蘭的限制，建立基于Matlab 的肩法蘭與人體上肢活動耦合模型。 肩法蘭與人體上肢活動耦合模型示意圖如圖4 所示，圖中不同顏色的圓環可視作位于不同空間位置的肩法蘭。

圖4 肩法蘭與人體上肢耦合模型示意圖Fig.4 Coupling model of shoulder flange and human upper limb

在耦合模型程序的運算中，在進行上肢結構與肩法蘭碰撞情況判定之前，需設定碰撞閾值，該閾值依據人體幾何參數選取。 本文選取上臂和前臂的半徑分別作為人體上臂和前臂的碰撞閾值。

以上肢的各個結構與肩法蘭的碰撞情況判定對應的上肢可達位置是否有效，若某一可達位置對應的上肢結構與肩法蘭的距離小于碰撞閾值，則認為此時人體上肢與肩法蘭發生碰撞，因此對應的上肢可達位置無效。

耦合模型以人體肩關節以及肘關節活動范圍作為輸入，以腕關節中心作為參考點，按照各個關節角度的耦合關系約束各關節角度的取值范圍，在6 個關節角度活動范圍內選取合適的步長進行循環迭代運算，以獲得相應的腕關節中心點位置。通過上肢結構與肩法蘭的碰撞判定，剔除上肢與肩法蘭發生碰撞所對應的標記點位置，即可獲得肩法蘭約束下人體上肢活動的可達域空間。

通過改變肩法蘭設計因素的參數，可得不同肩法蘭布局下人體上肢可操作空間的體積。 通過改變肩法蘭的4 個設計因素的參數，可運算獲得不同肩法蘭設計下的單、雙手可達域空間體積。

3 基于耦合模型的數值實驗

3.1 實驗設計

為探求肩法蘭對上肢活動的影響，以人體上肢活動能力作為實驗考察的因變量。 可達域是描述上肢活動能力的重要指標，臨床上常用可達域來測試、表征關節活動性能[7]，結合艙外航天服上肢組件活動性能研究中常用可達域作為評價指標[14]，本實驗利用可達域空間作為表征上肢活動性能的定量指標。

根據艙外服的使用背景定義了單手、雙手可達域空間體積2 種考察指標。 單手可達域空間體積是指單只手臂活動過程中可到達的空間區域的體積，實驗中以右手臂為實驗對象，利用耦合模型計算右手臂在肩法蘭約束下的可達域空間體積大小。 同時考慮到出艙活動中，大多數的任務需航天員雙手協同完成，僅考察單手空間不足以描述肩法蘭對人體上肢活動性的影響，因此定義了雙手可達域空間，也即左右雙手可同時到達、完成操作的空間區域，即左右單手可達域空間的交集空間。

正交實驗設計是安排多因素實驗、尋求最優水平組合的高效率實驗設計方法[15]。 根據正交實驗設計的特點以及本實驗研究需求，采用正交實驗方法設計實驗，并采用極差、方差以及回歸分析方法進行分析。

本實驗以建立的艙外服肩法蘭與人體上肢耦合模型為平臺，基于Matlab 程序開展計算機數值實驗，分別對肩法蘭的4 個設計因素進行賦值，完成單、雙手可達域空間體積的計算。

3.2 參數設置

首先需設定各個實驗因素的水平數及水平值。 根據Heather[3]研究，人體上肢在活動過程中，γ、α平均值的范圍分別為式(2):

依據艙外服上軀干結構的研制經驗及人體幾何尺寸標準，左右肩法蘭中心距l、肩法蘭內徑d的取值范圍設定見式(3):

李元豐等[4－6]根據上軀干結構的組成研制了上軀干結構原理樣機，并獲得了角度γ與角度α水平范圍的驗證，見式(4):

正交實驗因素水平設定如表1 所示。 實驗因素是肩法蘭的設計因素。

表1 正交實驗因素水平Table 1 Factor level of orthogonal test

由于實驗因素的水平數相同，且不考慮肩法蘭各設計因素間的交互作用，可選用L16(45)正交表安排實驗方案，如表2 所示。

表2 正交實驗方案Table 2 Orthogonal test plan

3.3 實驗結果

數值實驗設計因素及單、雙手可達域空間體積見表3。 通過對比發現，各種肩法蘭布局對上肢活動的限制非常明顯，且與單手可達域空間體積相比，雙手可達域空間體積受影響程度更大。

表3 單、雙手可達域空間體積結果Table 3 Results of one－hand and two－hand reachable domain space volume

根據正交實驗的分析方法，計算各個實驗因素的Ti及mi及R(表4)。 其中T為總體積，m為平均體積，i表示各因素的水平編號。 表中的最后一行為同一列的mi之中最大值與最小值的差，稱為極差，以R表示。 極差是衡量數據波動大小的指標，極差大說明該因素對考察指標的影響大，是主要影響因素；極差小就表示該因素對考察指標的影響小，是次要影響因素[16]。

表4 單、雙手可達域空間體積正交實驗分析結果Table 4 Orthogonal experiment analysis of one-hand and two-hand reachable space volume

通過對比極差的大小可知，在l、d、γ、α4 個設計因素中，對于單手操作空間體積，角度α因素是主要因素，以下因素按照重要性排序依次是l、d、γ；對于雙手操作空間體積，肩法蘭內徑d因素是主要因素，以下因素按照重要性排序依次是α、l、γ。

為了直觀地分析各個因素對上肢活動能力的影響，繪制了實驗因素與考察指標關系的趨勢圖(圖5)。

由圖5 可以看出，當左右肩法蘭中心距l為370 mm，肩法蘭內徑d為240 mm，角度γ為25°，角度α為60°時，單手可達域空間體積最大。

圖5 單手可達域空間體積與各影響因素關系趨勢圖Fig.5 Trend of relationship between the spatial volume of one-hand reachable domain and influencing factors

由圖6 可以看出，當左右肩法蘭中心距l為390 mm，肩法蘭內徑d為240 mm，角度γ為15°，角度α為60°時，雙手可達域空間體積最大。

圖6 雙手可達域空間體積與各影響因素關系趨勢圖Fig.6 Trend of relationship between the spatial volume of two-hand reachable domain and influencing factors

由于直觀分析法得到的最佳水平組合未出現在16 次實驗中，需進一步追加驗證實驗。 通過模型計算求出的最佳水平組合下單手可達域體積為255.7603 dm3，表明當左右肩法蘭中心距l為370 mm，肩法蘭內徑d為240 mm，角度γ為25°，角度α為60°時，肩法蘭對單手可達域空間體積的限制最小。

通過模型計算求出的最佳水平組合下雙手可達域體積為37.4354 dm3，表明當左右肩法蘭中心距l為390 mm，肩法蘭內徑d為240 mm，角度γ為15°，角度α為60°時，肩法蘭對雙手可達域空間體積的限制最小。

為準確估計誤差大小，評估各因素對上肢活動能力影響的顯著水平，采用多因素方差分析對實驗結果進行分析[17]。

單手可達域空間體積實驗數據的方差分析結果如表5 所示，可以看出，因素α 對單手可達域空間體積影響非常顯著，因素l、d、γ對單手可達域空間體積影響顯著。

表5 單手可達域空間體積方差分析Table 5 Variance analysis of one-handed reachable area volume

雙手可達域空間體積實驗數據的方差分析結果如表6 所示，可已看出，因素l、d、γ、α對雙手可達域空間體積影響都非常顯著。 以上分析結果與直觀分析法的結論一致。

表6 雙手可達域空間體積方差分析Table 6 Variance analysis of two-hand reachable area volume

通過對圖5 分析發現，單手可達域空間體積與d、α因素呈線性關系；與l、γ因素的關系無法以線性關系描述，應引入更高階次項。 設單手可達域空間體積為y1，左右肩法蘭中心距l、內徑d、角度γ、角度α分別是x1，x2，x3，x4。 設回歸模型為式(5):

式中，α0，α1，α2，α3，α4，α5，α6為回歸方程系數，對實驗數據進行回歸分析，可獲得回歸方程式(6):

通過對圖6 的分析發現，雙手可達域空間體積與l、d、γ、α因素都呈線性關系。 設雙手可達域空間體積為y2，左右肩法蘭中心距l、內徑d、角度γ、角度α分別是x1，x2，x3，x4。 設回歸模型為式(7):

式中，α0，α1，α2，α3，α4為回歸方程系數，對實驗數據進行回歸分析，可獲得回歸方程式(8):

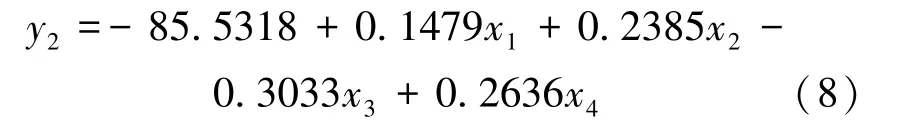
4 實驗驗證及預測結果

以身高為170 cm 男性為例，采用耦合模型計算無肩法蘭約束和有肩法蘭約束的上肢有效可達域空間。 根據GJB36A－200 和GB10000－88 中人體尺寸標準，模型中的人體參數設置如表7 所示，人體上肢活動角度范圍如表8 所示。

表7 人體模型參數Table 7 Parameters of human model

4.1 耦合模型實驗驗證

表9 為無肩法蘭約束人體上肢可達域空間體積的模型計算結果與文獻數據的對比，表明本文計算結果與Klopcar 等[7]研究相比差異很小，且處于文獻[7]的誤差區間內，說明本文模型對可達域空間體積的計算較準確，證明所建立的人體上肢可達域模型的有效性，可進一步用于肩法蘭與人體上肢耦合模型的研究。

表9 無肩法蘭約束人體上肢可達域空間體積對比Table 9 Comparison of spatial volume of human upper limb reachable area domain without shoulder flange /dm3

表10 為肩法蘭約束下上肢可達域空間體積的模型計算結果與文獻數據及實驗測量的對比，計算結果與李元豐等[4]研究相比差異很小，表明耦合模型對上肢可達域空間體積的計算較準確，證明所建立的肩法蘭與人體上肢耦合模型是有效的。 另外，同表9 中數據相比可知，肩法蘭對人體上肢可達域空間具有顯著影響。

表10 有肩法蘭約束人體上肢可達域空間體積對比Table 10 Comparison of spatial volume of human upper limb reachable area domain with shoulder flange /dm3

通過模型計算和實驗測量對比，雖然所建立的肩法蘭與人體上肢耦合模型在某些方面對肩法蘭與人體上肢活動關系描述尚有不足，但仍可以較準確地反映肩法蘭對人體上肢有效可達域空間的影響。

建模過程中，模型對人體上肢的結構進行了簡化，尤其是肩復合關節，雖然該簡化可以較好地表達上肢的運動特性，但對于幾何形態的描述缺乏足夠精度，會帶來一定偏差。 模型計算中，人體上肢的有效可達域空間是三維不規則形態，其邊界不是連續曲面，另外Matlab 軟件是通過擬合來計算可達域體積，難免導致誤差的累積。

受以上因素的影響，模型計算的結果與實驗結果存在一定的偏差，但考慮實驗操作、數據處理等過程的誤差，可以認為模型具備一定的合理性，可作為數值模擬實驗的平臺。

4.2 回歸模型預測效果

為驗證回歸模型的預測效果，本文設計了6次驗證實驗。 分別按照6 種不同的肩法蘭布局方案，將回歸方程得到的人體上肢單、雙手可操作空間體積擬合計算值與耦合模型程序運算得到的計算結果進行對比。 對比結果如圖7 所示，可以看出耦合模型與回歸模型符合程度較高。

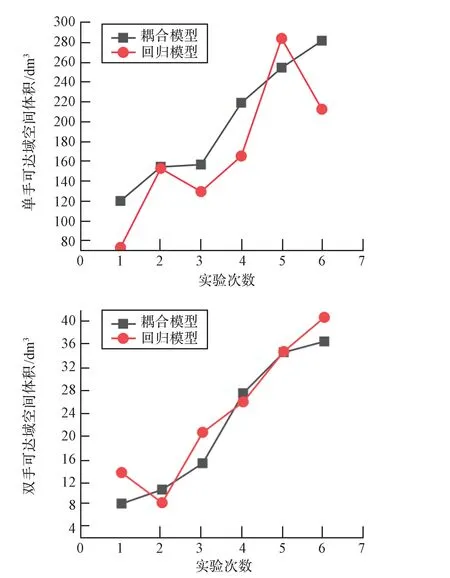
圖7 回歸模型預測效果Fig.7 Regression model prediction effect

考慮實驗操作、數據處理等過程存在的誤差，可以認為單、雙手可達域空間體積回歸模型的計算誤差在可接受范圍內，驗證了所建立的回歸模型的有效性。

5 討論

艙外服肩法蘭的設計因素包括左右肩法蘭中心距l、肩法蘭內徑d、角度γ和α，通過改變以上設計因素可實現肩法蘭布局的變換，肩法蘭布局的設計就是確定這4 種設計因素參數的過程。 上軀干肩法蘭結構與人體上肢活動具有顯著性相關性。 本研究通過計算機數值實驗研究肩法蘭與人體上肢活動的相關性，旨在明確肩法蘭的各個設計因素對上肢活動的影響，為進一步肩法蘭布局的改進優化提供依據。

在研究指標的設定上，本文提出了更能全面描述上肢活動能力的可達域空間體積指標。 實驗結果表明，單、雙手可達域空間體積指標可以有效區分不同肩法蘭布局形式對人體上肢活動的影響。

統計結果表明，肩法蘭的4 個設計因素對單、雙手可達域空間體積都有顯著或非常顯著的影響。 各個因素對單手操作空間相對體積的影響排序為α、l、d和γ。 各個因素對雙手操作空間相對體積的影響排序為d、α、l和γ。

根據前人研究得出各個實驗因素的交互作用項對上肢活動性的影響不顯著，因此本文在設計實驗方案時未包含交互作用因素。 從實驗結果分析，尤其是在回歸分析獲得的回歸方程中，d、α、l和γ影響顯著，可以有效地描述設計因素對上肢活動能力的影響，而方程中并不包含交互項，因此可以佐證各因素的交互作用對于上肢活動能力的影響并不顯著。

6 結論

本文基于肩法蘭與人體上肢耦合模型，采用數值實驗方法研究了航天服肩法蘭布局與人體上肢活動的關系，結論如下:

1) 單、雙手可達域空間體積指標可以有效地區分不同肩法蘭布局形式對人體上肢活動的影響，是衡量肩法蘭對人體上肢活動影響的有效指標。

2) 在肩法蘭的4 個設計因素中，角度α是影響單手操作空間的主要因素，其次是左右肩法蘭中心距l，肩法蘭內徑d以及角度γ。d是影響雙手操作空間的主要因素，其次是α，l以及γ。 肩法蘭的設計因素對單、雙手可達域空間體積有顯著的影響，可以采用關系式來描述。

3) 單、雙手可達域空間體積回歸模型可較好預測各種肩法蘭布局對上肢活動的影響，可用于肩法蘭布局方案的設計與評價，為未來艙外航天服軀干結構的設計提供參考依據。