基于動態變權重的空戰態勢評估
楊愛武,李戰武,李寶,奚之飛,高春慶
(1.空軍工程大學 航空工程學院,陜西 西安 710038;2.94916部隊,江蘇 南京 211500)
0 引言
空戰態勢評估是指在高對抗性環境下獲取目標態勢信息、綜合處理動態信息并量化顯示為態勢優劣情況,指導飛行員下一步決策占位。為了占據戰場態勢的優勢、先于敵方形成觀察、判斷、決策、行動(OODA)環、達到先敵發射的效果,飛行員需要快速機動占位,如何量化描述飛行員快速占位的動態過程,以及占位過程中的態勢動態變化情況,對于指導下一步決策具有十分重要的意義。
目前對于空戰態勢評估的研究主要分為態勢評估模型優化與改進以及態勢影響指標客觀權重的求解。文獻[1]提出了一種基于能力威脅、態勢威脅和意圖威脅的綜合威脅評估模型,通過態勢預測實現超視距目標威脅有效評估,豐富了態勢評估模型。文獻[2]提出一種基于導彈攻擊區的態勢評估模型,基于攻擊區來構造態勢優勢函數,評估模型與實際空戰特征貼合緊密。文獻[3]提出一種基于前景理論和灰色關聯分析-逼近理想點的權重優化方法,考慮飛行員主觀因素以及指標之間的關聯度,解決了態勢值求解中指標的相關性問題。文獻[4]提出一種基于改進層間相關性的重要性準則-線性回歸分析的客觀權重求解方法,減少主觀因素的影響。文獻[5]提出一種結合變權重理論來調整評估指標權重,進行近距空戰態勢評估的方法。文獻[6]提出一種主成分分析法以及智能算法的威脅評估方法,提高了評估模型的精度。上述態勢評估方法均在不同程度上改進了態勢評估模型以及優化指標權重,但也存在以下2點問題:一是在態勢評估模型中沒有體現出空戰的高動態性,多為當前態勢下的評估,沒有考慮未來態勢的影響;二是固定權重求解態勢值將導致態勢狀態與實際情況不相符的問題。
本文針對傳統態勢評估優勢函數描述戰斗機動態特性的薄弱性以及求解態勢值固定權重的不合理性,在傳統態勢優勢函數的基礎上優化態勢優勢函數,考慮機動強度和機動潛力對態勢的影響,建立機動強度和機動潛力模型;進而建立變權重模型,解決固定權值求解態勢狀態失衡問題。
1 空戰態勢評估模型
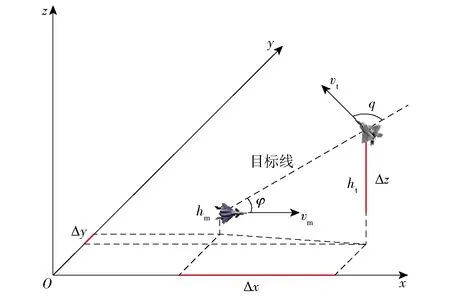
空戰態勢評估是綜合戰場上空間態勢、作戰能力以及戰術意圖等相關因素,判斷雙方當前態勢優劣性。空間態勢包含戰場態勢的幾何態勢信息,分為角度、速度、距離和高度,用以表示狀態信息的動態屬性;作戰能力包含戰斗機的靜態能力指標,可以分為機動能力、攻擊能力、探測能力、操縱能力、生存能力、航程能力以及電子對抗能力,用以表示特征信息的靜態屬性;戰術意圖包含戰斗機的行為動作,可以分為探測、突擊、攻擊、掩護、規避、干擾和逃逸,用以表示行為特征屬性,用實現某種戰術意圖的機動強度和機動潛力來定量表示[7]。空戰態勢關鍵因素模型如圖1所示。
1.1 空間態勢函數
空間態勢是指根據載機與目標之間的運動狀態信息來判斷優劣勢。空戰的關鍵在于讓目標處于載機攻擊區內而避免載機進入目標的攻擊區,對于攻擊區范圍影響較大的有角度、速度、距離和高度4種影響因素,基于此建立空間態勢優勢函數。
1.1.1 角度態勢函數
角度態勢函數的主要影響因素為目標方位角φ和目標進入角q,0 rad≤|φ|≤π rad,0 rad≤|q|≤π rad.|φ|越小、|q|越大,空空導彈攻擊區的范圍越大,角度態勢越好[8]。角度態勢函數可以表示為
(1)
(2)
式中:Tφ表示方位角優勢;Tq表示進入角優勢;φrmax表示最大搜索方位角,φmmax表示最大離軸發射角,φmkmax表示不可逃逸圓錐角,0 rad<φmkmax<φmmax<φrmax<π rad.
方位角和進入角之間對空戰態勢影響存在耦合關系,角度態勢函數可以表示為
(3)
式中:Ta表示角度優勢;γφ、γq表示方位角和進入角的權重,γφ+γq=1.
1.1.2 速度態勢函數
空戰中,速度增加會縮短戰斗機攻擊占位的時間,不可避免地帶來戰斗機能量消耗多、轉彎占位能力差等問題,因此,文獻[2]提出了我方最佳空戰速度v0,基于最佳空戰速度來建立速度態勢函數。
當v0>1.5vt時:
(4)
當v0≤1.5vt時:
(5)
式中:Tv表示速度優勢;vm表示載機速度;vt表示目標速度。
1.1.3 距離態勢函數
根據導彈攻擊范圍以及雷達探測距離,建立距離態勢函數如下:
(6)
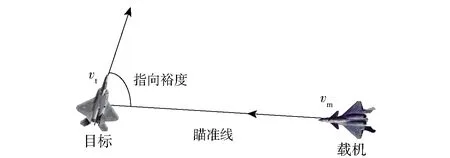
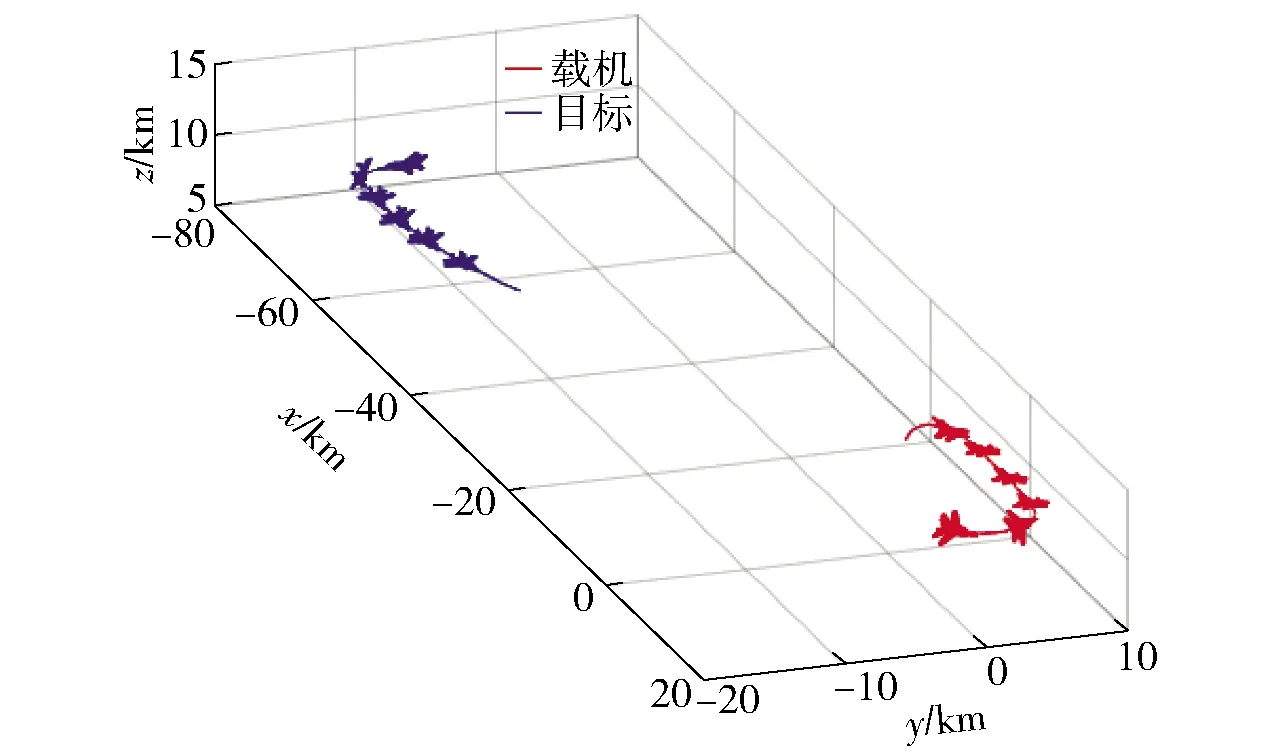
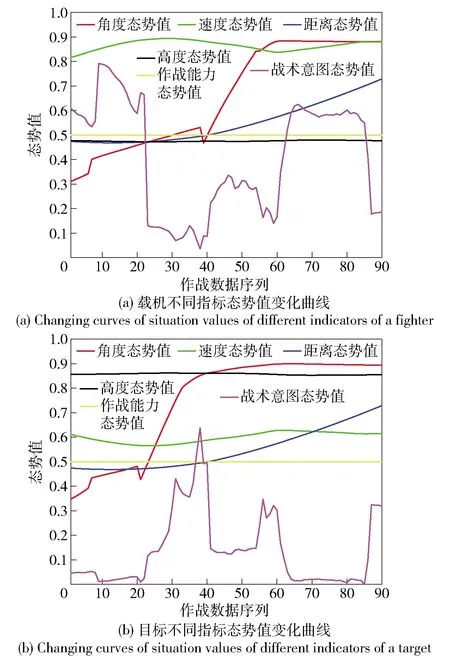
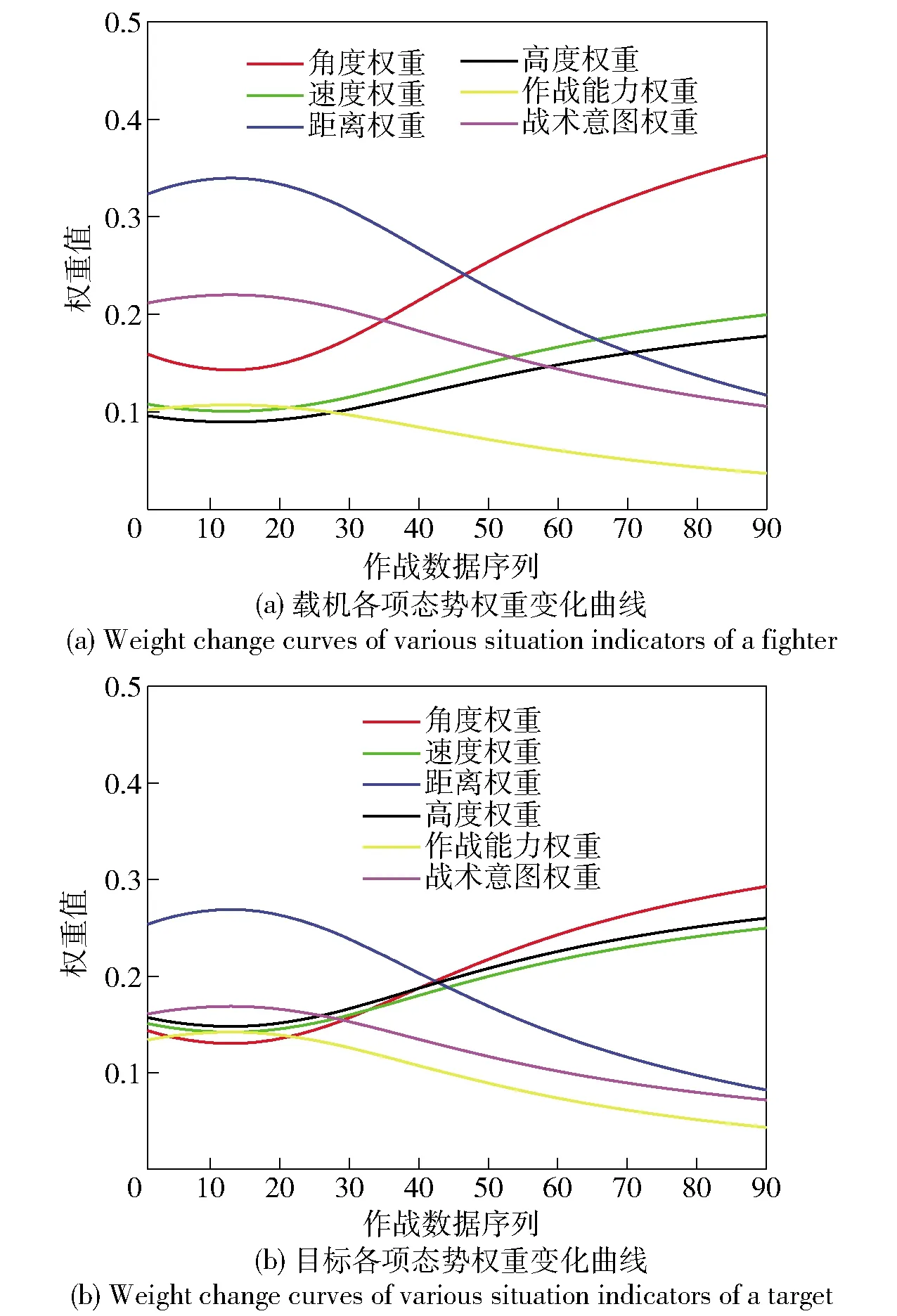
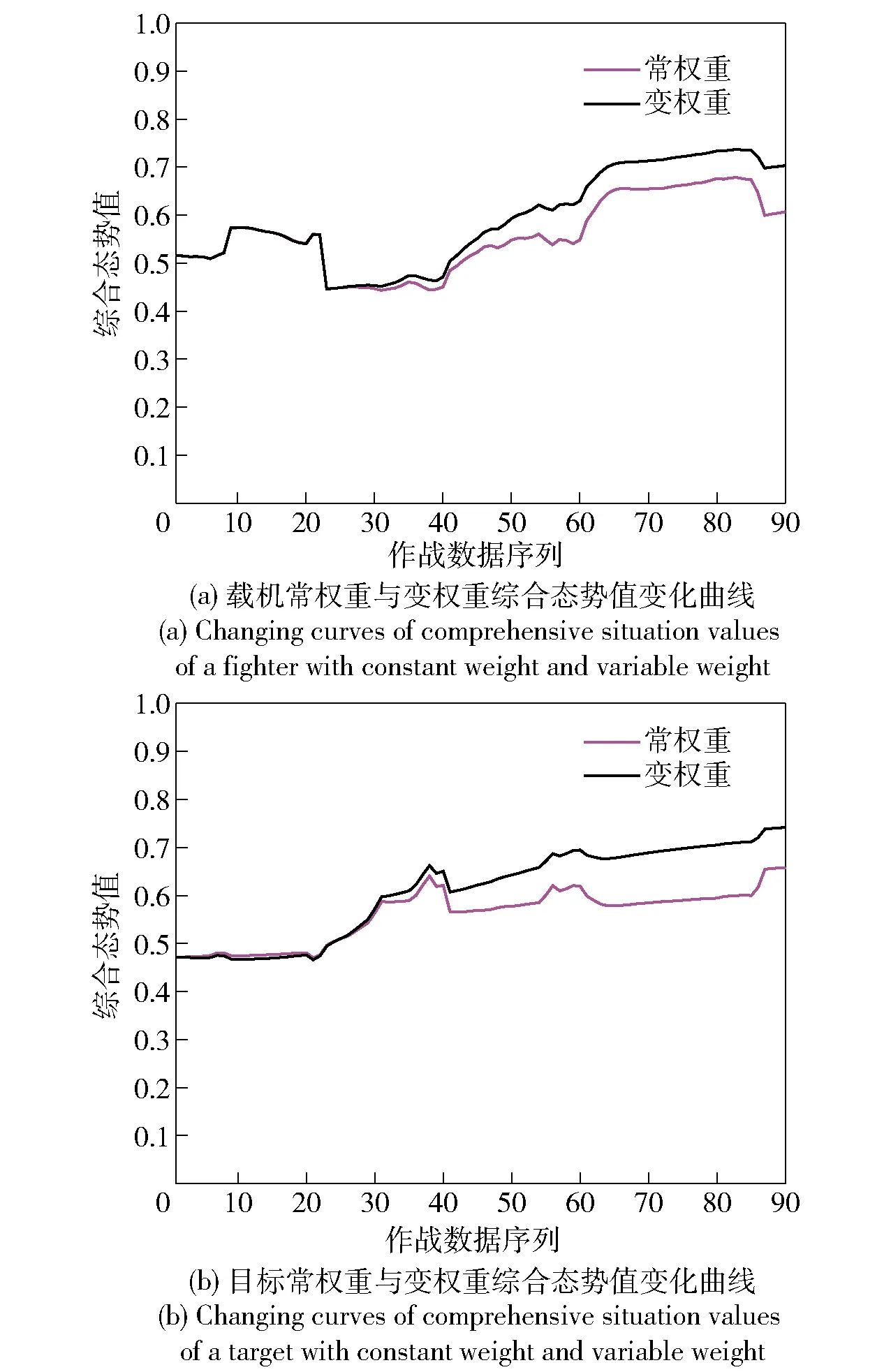
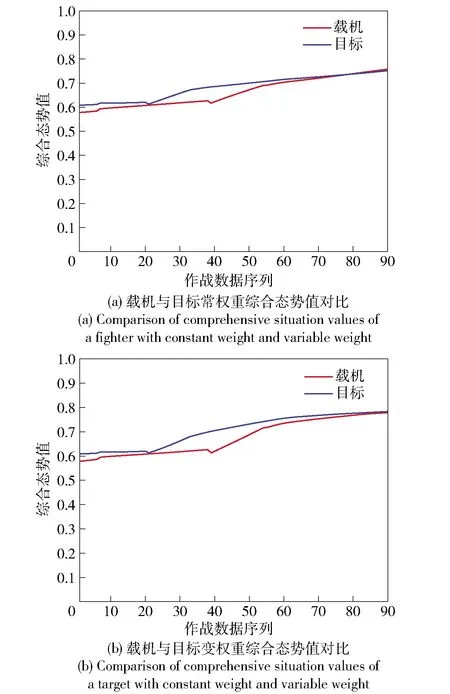
式中:Td表示距離優勢;D表示載機與目標之間的距離;Drmax表示雷達最大探測距離,Dmmax表示導彈最大攻擊距離,Dmkmax表示不可逃逸最大距離,Dmkmin表示不可逃逸最小距離,Dmmin表示導彈最小攻擊距離,Dmmin 1.1.4 高度態勢函數 空戰中,載機與目標之間的高度差增加會增加導彈的攻擊區范圍,不可避免地帶來對載機性能、導彈性能以及攻擊時垂直方向大過載等問題。因此,文獻[2]提出了我方最佳占位高度hbh,基于最佳占位高度建立態勢函數: (7) 式中:Th表示高度優勢;hm表示載機高度;ht表示敵機高度。 利用戰斗機靜態空戰能力指標[7]來評估其作戰能力: εmεsεcεe, (8) (9) 式中:T?表示作戰能力優勢;?m表示載機空戰能力;?t表示目標空戰能力。 戰斗機實現某種戰術意圖屬于動態過程,對態勢影響是動態變化的,意圖實施初始階段對我方威脅程度小,我方就可以在此階段提前做出機動決策避免陷入被動。以往的態勢函數將戰術意圖根據專家經驗直接給出態勢值,用具體數值直接表示一段時間的意圖威脅,未考慮意圖完成度、動態性,具有很強的主觀性,限制了我方機動決策范圍,從而導致空戰被動局面。本文提出機動強度和機動潛力描述這一動態過程,以避免戰術意圖固定值所帶來的限制問題。基于戰術意圖識別結果建立戰術意圖函數,通過機動強度和機動潛力量化戰術意圖態勢。戰術意圖函數可以表示為 (10) 式中:TI表示戰術意圖優勢;α表示戰術意圖威脅系數;MP表示機動強度;MS表示機動潛力。 綜上所述,綜合態勢函數可以表示為 f(Ta,Tv,Td,Th,T?,TI)=ωaTa+ωvTv+ωdTd+ ωhTh+ω?T?+ωITI, (11) 式中:ωa、ωv、ωd、ωh、ω?、ωI為不同態勢之間的權重,ωa+ωv+ωd+ωh+ω?+ωI=1. 在高對抗性空戰環境下,飛行員針對不同態勢情況選擇不同的機動方式,戰斗機做出一系列機動動作帶來的是態勢的急劇變化,態勢的相對變化情況可以用機動強度大小來描述。另一方面,戰斗機在實施機動后,其剩余機動能力對未來態勢的影響也是評估當前態勢需要考慮的因素之一,剩余機動能力可以用機動潛力的大小來描述。下面從機動強度和機動潛力的定義出發,建立機動強度和機動潛力的模型來分析戰斗機機動實施戰術意圖對態勢的影響。 機動強度可以定義為:機動強度主要用來描述空戰雙方對抗過程中一定時間內戰場態勢的相對變化情況,其表征的是戰斗機在實施某種作戰意圖時做出相應的機動動作帶來的態勢優劣性改變,即戰斗機雙方實現某種戰術意圖快速程度。相對態勢值變化率越大,即戰斗機所做出的空戰機動動作導致態勢的變化越劇烈,機動強度越大,表明戰斗機實現某種戰術意圖的想法越強烈,對另一方威脅程度就越大。 在態勢優勢函數中空間態勢函數和作戰能力函數計算的是當前時刻瞬時相對態勢,評估結果無法完全體現空戰對抗過程的博弈過程。究其原因是沒有考慮戰斗機的動態特性,沒能反映戰斗機在一定時間段內的態勢變化情況。因此,本文提出的機動強度從空間態勢值的變化率來描述,量化體現空戰對抗過程的動態特性。 在Δt時間段內,戰斗機態勢值的變化可以表示為 (12) 式中:Sr表示態勢值變化率;Δg表示綜合空間態勢函數變化量;φt、qt、vt、Dt、ht分別表示t時刻的方位角、進入角、速度、距離、高度信息;ω表示空間態勢權重。 令Δt=1 s,可以得到戰斗機的瞬時態勢變化率Sr0,戰斗機的瞬時態勢變化率反映了當前時刻戰斗機機動的劇烈程度。 空戰中,通過態勢函數計算得到的相同或者近似態勢值的目標,其威脅程度在一定程度上不能視為相同,需要考慮目標此時的瞬時態勢值變化率,若目標的瞬時態勢值變化率大,則說明目標實現某種戰術意圖的機動越強烈,威脅程度更大。則機動強度可以用載機與目標之間的相對瞬時態勢變化率表示為 (13) 式中:Srm0、Srt0分別表示載機與目標的瞬時態勢變化率。 由于載機與目標的瞬時態勢變化率存在負值的情況,MP可以表示為 (14) 戰斗機在實施某種戰術意圖進行高強度機動占位后,其剩余機動能力會大幅度縮減,將會影響后續空戰進程中態勢占優。因此,在空戰高對抗性過程中,既要合理安排占位的機動強度,也要保持一定的剩余機動能力,避免陷入被動局面。 為了描述戰斗機的剩余機動能力,引入機動潛力的概念,機動潛力表征的是當前時刻空戰雙方相對潛在機動能力的物理量,其與飛機性能、當前時刻狀態以及雙方的相對位置關系相關[9]。機動潛力描述的是一種敵我雙方之間的相對關系,與態勢評估的優勢函數以及機動強度描述的當前時刻狀況不同,機動潛力是對未來空戰態勢的可能性比較,與飛行員選擇的機動方式相關。 機動潛力包含敵我雙方之間的相對機械能、相對單位剩余功率(SEP)以及指向速率比: MP=Re·Rs·Rv, (15) 式中:Re表示相對機械能;Rs表示相對SEP;Rv表示指向速率比。 2.2.1 相對機械能 戰斗機所蘊含的機械能為動能和勢能之和,戰斗機的機械能越高,飛行員的可操作性能越強,空戰優勢越明顯。 (16) 式中:Em、Et分別表示載機與目標的機械能;mm、mt分別表示載機與目標的質量。 2.2.2 相對SEP 戰斗機在對抗過程中,盡可能占據最佳高度,原因在于可以通過降低自身的高度減少部分勢能來占據有利態勢位置。SEP[10-11]用來表示戰斗機的爬升性能以及加速性能,是指在一定的發動機推力和阻力下戰斗機能量高度隨時間變化的過程,其計算公式如下: (17) 式中:P和f表示戰斗機瞬時推力和阻力;G表示戰斗機重力;v表示瞬時速度。載機與目標之間的相對SEP可以表示為 (18) 式中:am、at分別表示載機、目標瞬時加速度。 由于載機和目標的加速度存在負值情況,相對SEP可以表示為 (19) 2.2.3 指向速率比 戰斗機空戰過程中,角度態勢對于綜合態勢的影響較大,僅從機械能角度難以全面地描述機動占位后的機動潛力。同時,角度優勢中也蘊含著能量關系,具有角度優勢的戰斗機能夠減少機動量,即減小能量的消耗。下面參考文獻[9]提出的指向速率比來描述在角度上的機動潛力。 指向裕度用來評估戰斗機機頭方向指向目標的快慢程度,是一種空戰敏捷性指標,表示為戰斗機速度方向指向線與瞄準線之間的夾角。如圖2所示,載機速度指向敵機,目標需要轉動角度才能指向載機。借用指向裕度概念來表示指向速率比,載機與目標都是指向對方的側向而避免被對方指向側向,用指向速率比來描述指向對方的快慢程度。如圖3所示,方位角和進入角的變化速率分別表示載機和目標的指向速率,則指向速率比可以表示為 圖2 指向裕度示意圖 圖3 空戰角度關系 (20) 式中:ω(vm)、ω(vt)分別表示載機與目標在當前速度下的轉彎速率。 常權重考慮指標之間的相對重要度而被廣泛應用,變權重理論則還要考慮對狀態均衡性的偏好[12],是在常權重基礎上根據指標屬性進行懲罰性變權重和激勵性變權重。變權重理論首先需要確定指標之間的初始常權重,CRITIC法[13-14]是由Diakoulaki提出的客觀賦權方法,通過結合指標間的沖突性和數據變異對指標權重影響來確定權重[7]。本文基于CRITIC法確定初始權重,結合變權重理論構建變權重向量確定動態變權重。 CRITIC法確定態勢初始權重步驟如下: 步驟1構建態勢評估矩陣。 態勢評估矩陣由t個時刻構成實時評估狀態信息集Q={Q1,Q2,…,Qt}和p個態勢評估指標構成指標集N={N1,N2,…,Np}組成,第i時刻的第j項指標值為uij,則態勢評估矩陣表示為 (21) 步驟2規范化評估矩陣。 對于效益型、成本型和固定型指標進行規范化處理,以消除指標類型以及量綱的影響: 1)效益型指標 (22) 2)成本型指標 (23) 3)固定型指標 (24) 式中:θ為固定型指標最佳取值。經過規范化處理后得到態勢矩陣為Z=[zij]t×p. 步驟3計算評估指標之間綜合信息量。 指標之間沖突性和數據間的對比強度由相關系數rkl和標準差sj來表示,評估指標之間的綜合信息量為 (25) 式中: (26) rkj=cov(Nk,Nj)/(sk,sj), (27) Nk為第k項指標,Nj為第j項指標。 步驟4確定評估指標常權重。 通過評估指標的綜合信息量可以確定指標之間的常權重向量為 w=(w1,w2,…,wj,…,wp), (28) 相應的變權向量W(X)可以表示為 W(X)=[w1(X),w2(X),…,wj(X),…,wp(X)]= W(x1,x2,…,xj,…,xp), (29) 式中:xj為第j項態勢評估指標變權重。 變權重的主要方法為構造狀態變權重向量實現對狀態的加權調整,避免狀態不均衡。狀態變權重向量可以表示為映射關系[12]: Sx:[0,1]p→[0,1]p,X→Sx(X)=Sx·X= [S1(X),S2(X),…,Sj(X),…,Sp(X)]· (x1,x2,…,xj,…,xp)= [S1(X)·x1,S2(X)·x2,…,Sj(X)·xj,…,Sp(X)·xp]. (30) 變權重向量W(X)可以通過狀態變權重向量Sx與常權重向量w的Hadamard乘積得到: (31) 變權重求解的核心在于根據角度、速度、距離、高度、作戰能力,以及戰術意圖指標對空戰態勢影響程度構建均衡函數,通過均衡函數求導來計算狀態變權重向量。其計算公式如下: (32) 式中:B(x)表示態勢評估指標x的均衡函數。 隨著雙方交戰距離的靠近,角度、速度、高度指標對態勢的影響程度越來越大,雙方從中距再到近距都處于對方的探測范圍之內,需要戰斗機機動占位構成攻擊條件,用正相關非線性函數進行激勵性變權重,均衡函數[15]表示為 (33) 式中:βj為變權重因子,j=1,2,…,5,βj>0為激勵性變權重,βj<0為懲罰性變權重。 另一方面,距離、作戰能力指標對態勢的影響程度隨著距離縮進越來越小,影響空戰勝負主要在于優先構成攻擊條件,用非線性函數進行懲罰性變權重,均衡函數表示為 Bj=xj+βjlnxj,j=3,5. (34) 戰術意圖態勢屬于動態的過程,體現了戰斗機的占位過程和潛力趨勢,在空戰的每一個階段都很重要,用1階線性函數表示為 Bj=xj,j=6. (35) 基于此分析,綜合均衡函數表示為 (36) 各指標的狀態變權重向量表示為 (37) 綜上所述,各指標的變權重表示為 (38) 選取空戰對抗仿真中記錄的部分數據作為數據樣本進行態勢評估,空戰雙方對抗軌跡如圖4所示。選取45 s空戰對抗數據進行算例分析,共90組數據,數據間隔為0.5 s,戰場初始信息表示如表1所示。 表1 空戰初始信息表 圖4 空戰對抗軌跡 根據文獻[16]提出的戰術意圖識別方法,識別出目標的戰術意圖為攻擊,根據專家經驗知識確定不同戰術意圖威脅系數取戰術意圖威脅系數為0.9.在作戰能力上,雙方戰斗機的作戰能力相當,作戰能力態勢值T?=0.5.結合機動強度和機動潛力的態勢評估模型,計算出雙方態勢指標值如圖5所示。 圖5 各項態勢指標變化曲線 從圖5中可以看出:此階段空戰對抗過程,載機占據速度優勢,目標占據高度優勢;在初始階段和末尾階段,從機動強度和機動潛力體現出載機實現攻擊戰術意圖想法較目標更加強烈,載機戰術意圖優勢更大;中間階段目標表現出的戰術意圖優勢更加明顯;戰術意圖態勢體現了空戰對抗過程的博弈性和高對抗性。 根據CRITIC法,確定載機與目標各項態勢影響因素的客觀常權重分別為wm=(0.154 3, 0.107 4,0.315 0,0.097 6,0.105 7,0.220 1),wt=(0.142 1,0.154 3,0.252 8,0.161 0,0.126 7,0.163 0). 通過對態勢指標影響程度分析建立均衡函數,結合變權重理論確定載機與目標各項態勢指標客觀變權重變化曲線,如圖6所示。從圖4、圖6中可以看出,載機與目標均采取側向接敵的策略,雙方的作戰距離先增加、后減小,由此可以得到態勢指標權重的變化趨勢,即隨著雙方作戰距離的變化,角度、速度、高度態勢權重先減小后增加,距離、作戰能力、戰術意圖態勢權重先增加后減小。 圖6 權重變化曲線 通過常權重和變權重求解的綜合態勢值如圖7所示。從圖6、圖7中可以看出:各項指標對態勢的影響程度隨著作戰距離變化,最終會影響綜合態勢值;在初始階段,載機與目標側向接敵,距離變化范圍較小,常權重與變權重綜合態勢值基本保持一致,但隨著作戰距離的減小,載機與目標迎頭接敵,載機保持較高的角度、速度優勢,目標則是較高的角度、高度優勢,且角度、速度、高度影響權重變大。另一方面,距離權重減小帶來的變化不足以抵消角度態勢增加的變化,且作戰能力和戰術意圖整體上保持相對較小的態勢,因此態勢值均有所提高,相比于常權重,變權重符合實際對抗過程,所評估出的態勢值更加合理,驗證了變權重求解的合理性。當戰術意圖為動態值時,通過常權重和變權重求解的綜合態勢值如圖8所示。 圖7 常權重與變權重綜合態勢值變化曲線 圖8 戰術意圖為動態值綜合態勢值對比圖 從圖8中可以看出,在末尾階段,常權重求解態勢值載機的優勢保持在0.08,變權重求解態勢值載機的優勢保持在0.02.從圖5的實際各項指標態勢值來看,載機與目標都保持相對較高的角度態勢值0.9,載機速度優勢值0.85高于目標速度優質值0.62,載機高度優勢值0.48低于目標高度優勢值0.85,雙方的距離優勢值0.65相當,作戰能力優勢值0.5相當,載機的作戰意圖優勢0.58高于目標作戰意圖優勢0.02,載機占據態勢上的優勢。從圖6的權重變化曲線來看,在末尾階段,載機角度權重增大范圍大于目標,但是目標高度、速度增大范圍大于載機,且載機距離減小范圍大于目標,作戰能力與戰術意圖權重變化范圍相當。實際上,載機存在態勢優勢,但優勢并沒有常權重計算得到的那么明顯,表明變權重求解能夠解決態勢評估中的狀態失衡問題。 當戰術意圖為固定值時,通過常權重和變權重求解的綜合態勢值如圖9所示。載機和目標的機動強度和機動潛力如圖10所示。 圖9 戰術意圖為固定值綜合態勢值對比 圖10 戰術意圖動態性對比 從圖8、圖9中可以看出,當將戰術意圖態勢值設置為固定值時,不考慮戰術意圖的完成性和動態性,與考慮機動強度和機動潛力的戰術意圖動態值對比,無論是常權重求解還是變權重求解,載機在大部分時間處于態勢的劣勢,且初始階段和末尾階段的優勢沒有體現出來,原因是被戰術意圖固定值所限制,這與實際情況不符。從圖10中可以看出,在初始階段和末尾階段,載機的速度、角度一直處于優勢,態勢變化更加劇烈,機動強度高于目標,并且載機存在一定程度上的機動潛力優勢,在中間階段,目標的機動強度與機動潛力相比于載機存在優勢,因此將戰術意圖設置為專家經驗的固定值,不考慮其動態變化對空戰實際態勢的評估存在一定程度的影響。 綜上所述,本文所提結合機動強度和機動潛力的變權重態勢評估方法能夠較為客觀地評估空戰對抗實際過程中的態勢變化情況,為下一步飛行員的機動決策打下基礎。 本文針對空戰態勢評估中的戰術意圖為固定值時對戰斗機動態特性以及博弈過程描述不充分,導致評估結果與實際態勢不相符問題,以及常權重求解態勢值導致的狀態失衡問題,提出一種動態變權重的空戰態勢評估方法。得出主要結論如下: 1)針對空戰動態性問題,在現有研究基礎上建立了包含空間態勢、作戰能力以及戰術意圖態勢評估模型,提出了機動強度以及機動潛力的概念,并建立了機動強度和機動潛力模型,用瞬時態勢變化率來量化機動強度以及用相對機械能、相對單位剩余功率SEP、指向速率比來量化機動潛力,綜合成新的戰術意圖態勢函數,改進了態勢評估模型,解決戰術意圖態勢為固定值帶來的評估結果偏差,進而導致機動決策范圍受到限制問題; 2)針對狀態失衡問題,提出了基于CRITIC法計算客觀權重,通過空戰態勢指標在對抗過程中對態勢的影響程度分析,構建符合實際空戰特點的均衡函數以及狀態變權重向量,基于變權重理論得到空戰態勢指標變權重,仿真得出態勢評估值更加貼合實際態勢狀態,所提方法能夠解決態勢中的狀態失衡問題。1.2 作戰能力函數
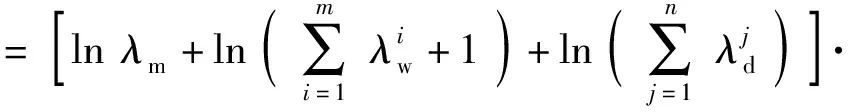
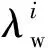
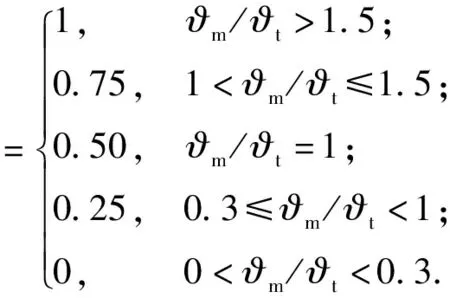
1.3 戰術意圖函數
2 機動強度和機動潛力模型
2.1 機動強度模型
2.2 機動潛力模型
3 基于CRITIC-變權重理論的動態變權重
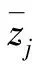

4 仿真算例與分析

4.1 態勢評估指標值求解
4.2 指標變權重求解
4.3 綜合態勢值求解
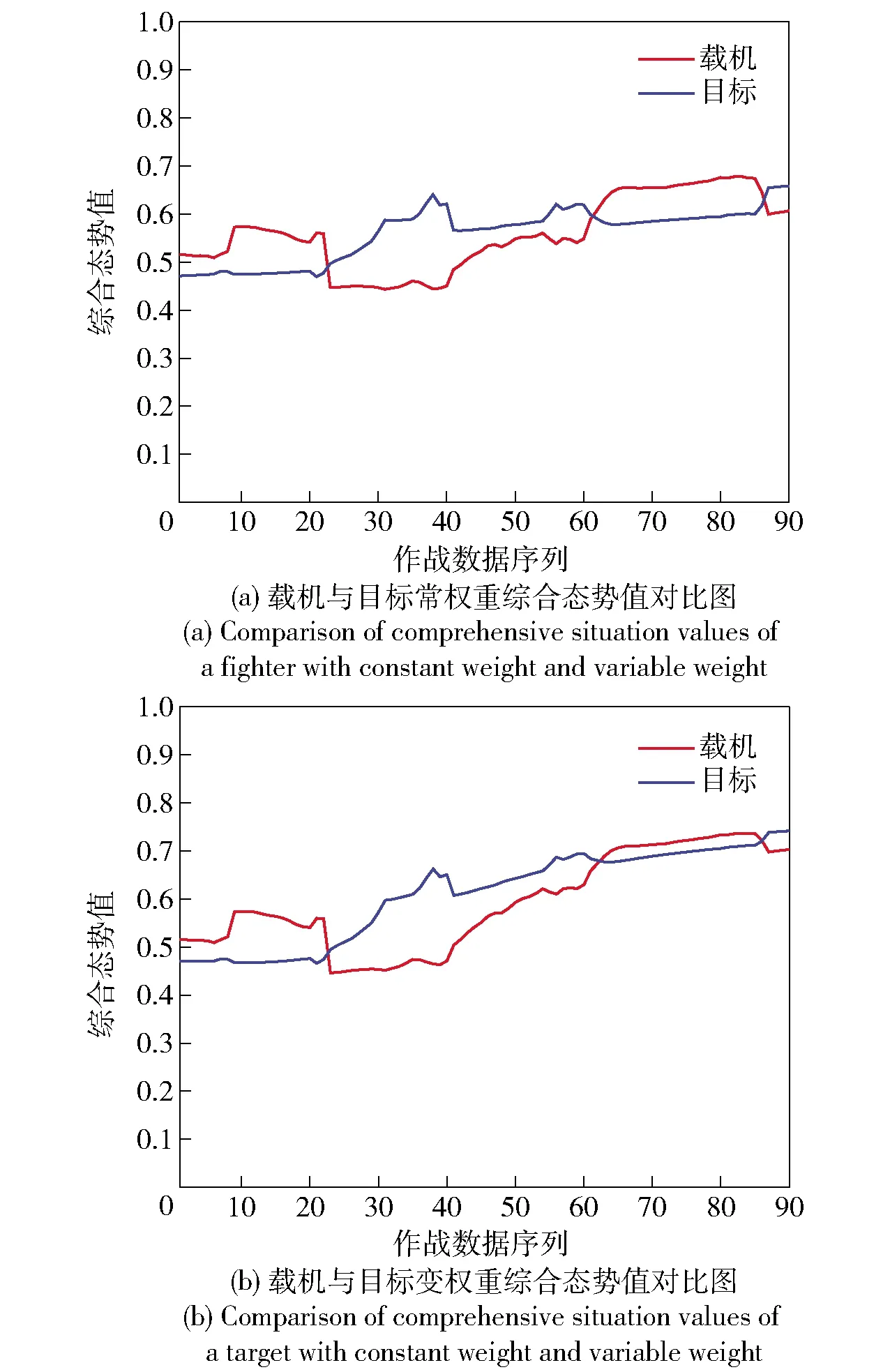
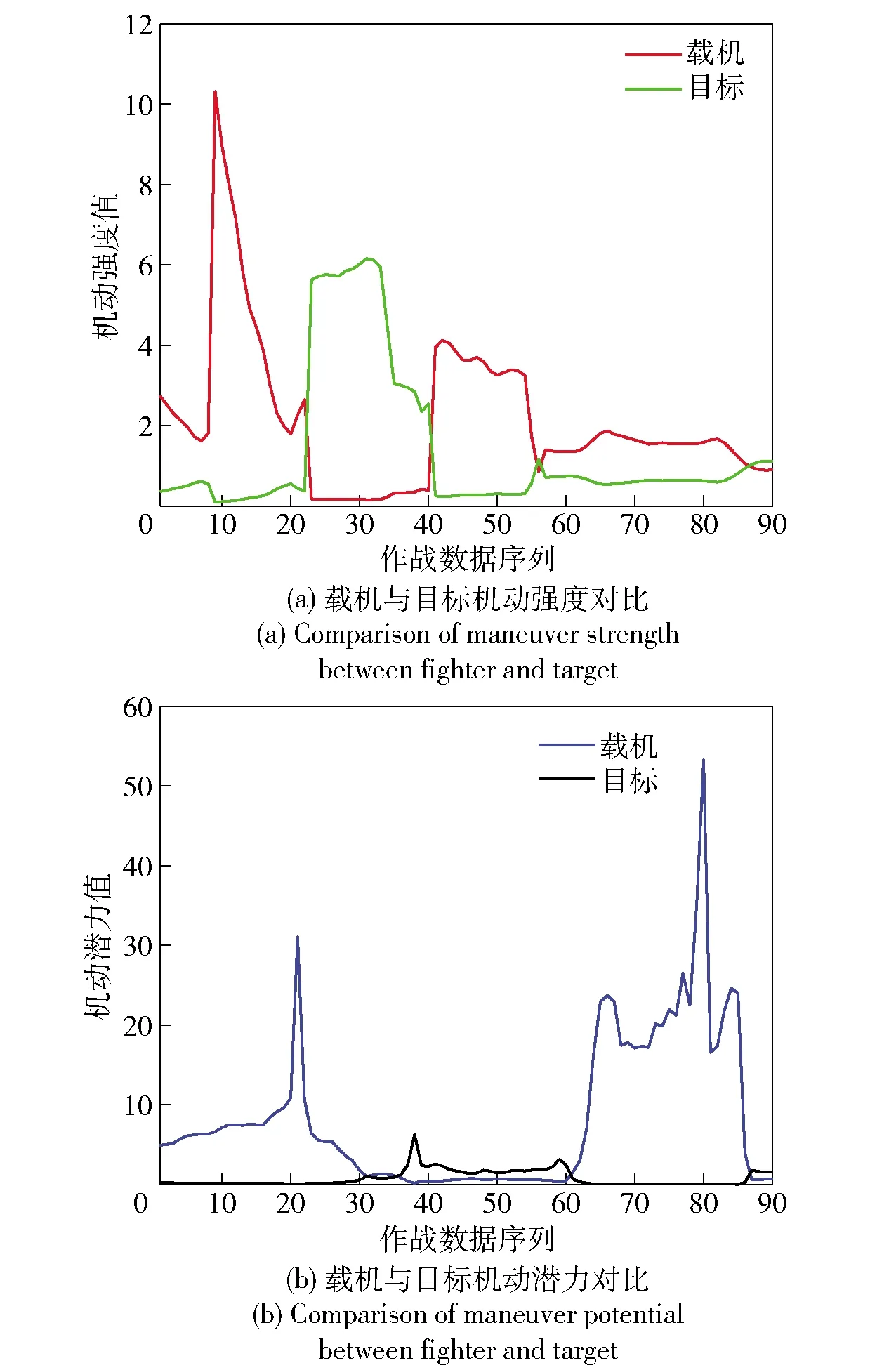
4.4 戰術意圖動態性對比分析
5 結論

