基于改進相似性的裝備部件剩余壽命預測及經濟性儲備策略
陳云翔,饒 益,蔡忠義,王澤洲
(空軍工程大學裝備管理與無人機工程學院,陜西 西安 710051)
0 引 言
在裝備實際使用過程中,對裝備性能狀態的掌握是裝備管理的重要工作之一,剩余壽命預測是故障預測和健康管理的關鍵技術[1-3]。通過對裝備關鍵部件剩余壽命的評估,掌握裝備完好性水平,可以為裝備的維修決策和部件儲備策略提供參考。合理制定裝備部件的儲備策略,從而提升裝備使用可靠性與經濟性,提高裝備的維修保障效能。
為進一步提高維修決策的科學性,基于剩余壽命的維修決策成為了研究的主流,基于裝備部件的剩余壽命進行維修決策、制訂相應的部件儲備策略,有利于實現維修保障精細化的現實要求。文獻[4]由已知的設備壽命分布函數預測其平均剩余壽命,以平均剩余壽命為閾值制訂預防性維護維修策略。文獻[5]基于剩余壽命預測信息,進行考慮替換時間和備件訂購時間的聯合決策。文獻[6]基于設備剩余壽命信息進行維修與備件訂購的聯合策略優化,以達到降低設備檢修成本和備件成本的目的。在基于剩余壽命的維修決策研究中,大多是基于狀態預測或基于統計回歸方法開展剩余壽命預測進而進行維修決策[7-8]。然而在實際應用中,裝備部件種類多、復雜度高,基于狀態預測和基于統計回歸的方法難以獲得合適的狀態變量預測模型,從而會影響到剩余壽命預測的準確性和維修決策的科學性,限制了其在工程領域的應用。
為了解決上述問題,工程實踐中常采用基于相似性的方法來預測裝備部件的剩余壽命。基于相似性的壽命預測方法通過度量參考樣本與服役樣本之間性能狀態的相似性,對服役樣本的剩余壽命進行預測,其主要思想可以表述為:若服役部件的近期性能狀態與參考部件性能退化情況在某時間內相似,則其有相似的剩余壽命,且相似性越高,剩余壽命相似概率越大[9]。其中,參考部件是與服役部件的同類部件,在相同條件下運行且已經失效。許多學者在基于相似性的剩余壽命預測方面開展了廣泛研究,文獻[10]提出了一種基于相似性的剩余壽命預測方法,并驗證了其結果優于神經網絡的預測結果。文獻[11]對衡量相似性的不同距離函數進行對比分析,表明當隨機干擾較小時,歐氏距離的預測準確度最高。文獻[12]提出了基于多參數融合相似的壽命預測方法對民航發動機進行壽命預測。然而,上述基于相似性的剩余壽命預測研究均認為參考部件與服役部件的運行條件相同[9,13-15],忽略了裝備使用過程中環境差異性對剩余壽命預測結果的不確定影響,降低了預測的準確性。在裝備的實際運行過程中,外界環境的變化和擾動等因素會導致運行條件的變化,使得部件退化的不確定性增大,從而導致部件之間性能狀態的差異性增大,相似性降低。若不考慮環境變化的影響而直接采用參考部件對服役部件的剩余壽命進行預測,將會產生不確定誤差,不利于后續維修決策和制訂儲備策略的有效開展。
針對現有研究的不足,本文提出一種基于改進相似性的裝備部件剩余壽命預測及經濟性儲備策略。首先,考慮環境擾動對裝備部件運行條件的影響,提出裝備部件分類方法,并由此建立基于改進相似性的剩余壽命預測模型。然后,基于剩余壽命預測信息,以裝備部件維修儲備總費用最低為目標,以資源利用率為約束,建立裝備部件經濟性儲備策略決策模型,實現最優的儲備策略。最后,通過某型裝備使用實例分析,驗證了方法的科學性和合理性。
1 基于改進相似性的裝備部件剩余壽命預測
根據已知的參考部件全壽命性能狀態檢測數據,將服役部件早期性能狀態檢測數據與其進行相似性度量,根據不同參考部件的相似度確定其權重,相似度越高,則權重越大。通過參考部件的壽命信息加權平均確定服役部件剩余壽命[16]。同類裝備部件在相同運行條件下使用時,其性能退化趨勢趨于一致,而運行條件變化會導致性能退化趨勢改變,相似性降低。
針對傳統的基于相似性的方法未考慮環境擾動導致運行條件變化的問題,本文考慮裝備部件運行條件的變化,對傳統的基于相似性的方法進行改進。基于系統聚類,利用性能狀態檢測情況對參考部件進行分類,區分不同運行條件下的參考部件。利用GA-BP(genetice algorithm-back propagation)網絡對參考部件分類結果進行訓練,將服役部件作為測試集對其類別進行區分。對分類后的服役部件在其類別內與參考部件進行相似性度量,從而以裝備部件運行條件為區分,對裝備部件剩余壽命進行更為準確的預測,更加符合實際情況。
1.1 基于系統聚類的參考部件分類
系統聚類是統計學中的典型聚類方法,系統聚類方法具有操作簡便、易于實現,分類快速準確等優點。其基本過程為:首先將所有樣本各自分為一類,然后根據各樣本的距離遠近對樣本各分類逐步進行合并,直至所有樣本歸為一類。
結合系統聚類的思想,利用參考部件全壽命性能狀態檢測數據對參考部件進行分類,確定合理的分類數目,區分不同運行條件下的參考部件。
1.2 基于GA-BP的服役部件分類
傳統BP網絡中初始權值和閾值對輸出結果影響較大,初始權值和閾值的隨機性可能導致結果局部最優、訓練次數較多、收斂速度較慢等問題。GA-BP網絡將GA算法和BP網絡相結合,首先利用GA算法進行全局尋優,優化BP網絡的權值和閾值,再利用BP網絡進行訓練,從而提高訓練速度和精度,增強BP網絡的魯棒性。GA-BP流程如圖1所示。
通過GA-BP網絡對參考部件的分類結果進行訓練,利用訓練好的神經網絡,將服役部件早期性能狀態檢測數據作為測試集進行識別與分類,得到服役部件的分類結果,區分其運行條件,從而實現參考部件和服役部件的聚類,區分環境擾動下運行條件相同的部件。
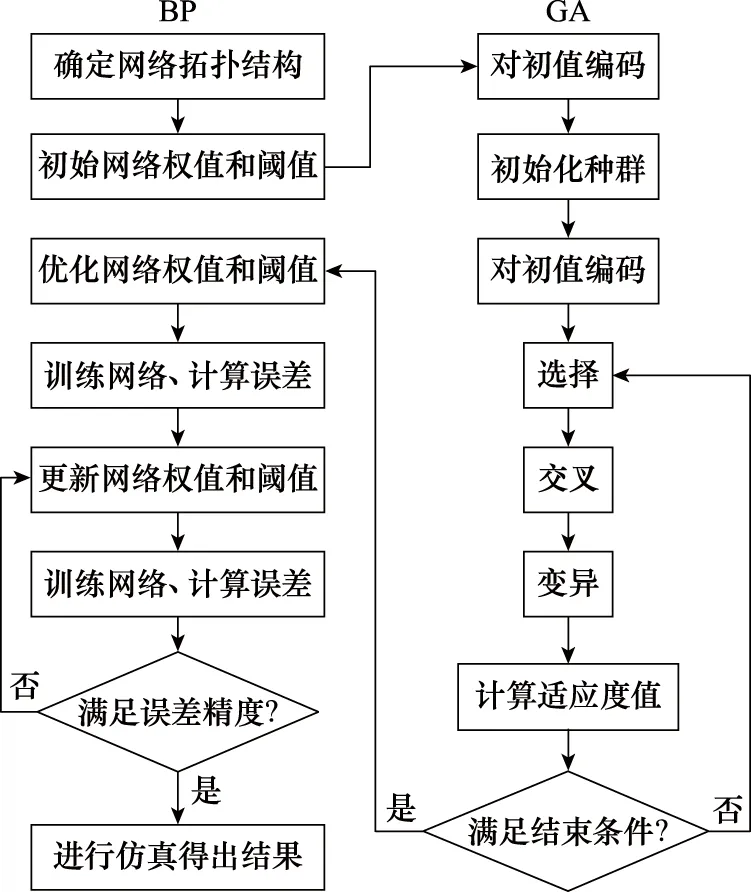
圖1 GA-BP網絡流程Fig.1 Process of GA-BP network
1.3 基于歐氏距離的相似性度量
設某運行條件類別下有n個參考部件,其全壽命性能狀態時序檢測數據形式為Xk={xk1,xk2,…,xkq},服役部件數為m,其早期性能狀態時序檢測數據形式為Xi={xi1,xi2,…,xip}。歐式距離原理簡單并且能夠包含兩個序列中每對對應點之間的差異信息,在時間序列相似性度量中經常被使用。選取歐式距離度量服役部件與參考部件的相似度,確定區分類別后的服役部件與參考部件的歐氏距離:
(1)
式中:i表示該類別內第i個待預測壽命的服役部件;k表示該類別內第k個參考部件;xij和xkj分別表示在第j次對裝備部件的檢測時部件的性能狀態數據;li為第i個服役部件的早期性能狀態檢測次數。歐氏距離越大,相似度Si k越小:
(2)
1.4 權重分配
對于同一個服役部件,與其歐式距離最小的參考部件即相似度最高的參考部件應該被賦予較大的權重,因此歐式距離越小時權重越大。對不同參考部件的賦權公式為
(3)
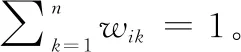
1.5 剩余壽命預測
由參考部件的全壽命性能狀態檢測數據可以得出參考部件的失效壽命,根據式(1)~式(3),服役部件的剩余壽命預測公式為
(4)
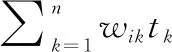
2 基于剩余壽命預測信息的裝備部件經濟性儲備策略
剩余壽命是反映裝備狀態的綜合指標,對裝備部件預測剩余壽命的最終目的是根據剩余壽命和實際需求得出經濟的裝備部件儲備策略,作為維修決策的重要依據。設服役部件數為α,部件更換費用為e1,訂貨費用為e2,缺件損失費用為e3,存儲費用為e4,訂貨周轉期為t1,訂貨周期為t2。其中,更換費用指更換部件所需費用;訂貨費用指下達訂單和部件輸送等所需費用;缺件損失費用指部件到壽后由于缺少備件導致缺件造成的損失費用;存儲費用是指存儲保存部件所需費用;訂貨周轉期指從訂單下達到部件到貨所需時間;訂貨周期表示在兩次訂貨的時間間隔。在本文中,主要探究部件維修儲備總費用最小時的部件儲備問題,即經濟性儲備。本文中的裝備部件為不可修件,且為避免浪費資源,僅考慮到壽更換和故障后更換兩種維護維修操作,到壽更換與故障后更換均可達到修復如新,假設各種維修更換操作瞬間完成,時間忽略不計。
2.1 經濟性儲備策略決策模型
根據經濟性原則,基于預測的裝備部件剩余壽命信息,建立以下模型。
維修儲備總費用為
W=GH+DH+CC+QH
(5)
式中:W為總費用;GH,DH,CC,QH分別為更換總費用、訂貨總費用、存儲總費用、缺件損失總費用。
更換總費用為
(6)

更換費用為
GHq=e1min(KCSq+DHSq,Nq)
(7)
式中:GHq為第q個訂貨周期的更換費用;KCSq,DHSq,Nq分別為第q個訂貨周期期初的庫存量、訂貨量和周期內部件需求量。庫存量由上一訂貨周期訂貨量與庫存量及部件維修更換量來確定;訂貨周期內部件需求量由在本訂貨周期到壽的部件數量確定。
訂貨費用為
(8)
存儲費用為
(9)
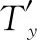
缺件損失費用為
(10)
綜上,以裝備部件維修儲備總費用最低為目標函數,以資源利用率為約束,建立裝備部件的經濟性儲備策略決策模型:
minW=GH+DH+CC+QH
(11)
(12)
式中:z為部件的維修更換次數;q為訂貨周期數;v為總訂貨周期數,可表示為
2.2 模型尋優求解
本文采用差分進化算法對模型進行尋優求解,差分進化算法是由Storn等人于1995年提出的一種全局優化算法[17],是基于種群的啟發式搜索算法,通過變異、交叉以及選擇操作在進化過程中不斷提高種群適應度,逐漸收斂至最優解附近。相較于粒子群算法、遺傳算法等典型進化算法,差分進化算法在魯棒性、算法控制參數規模等方面具有顯著優勢[18-19]。
差分進化算法的流程如圖2所示。
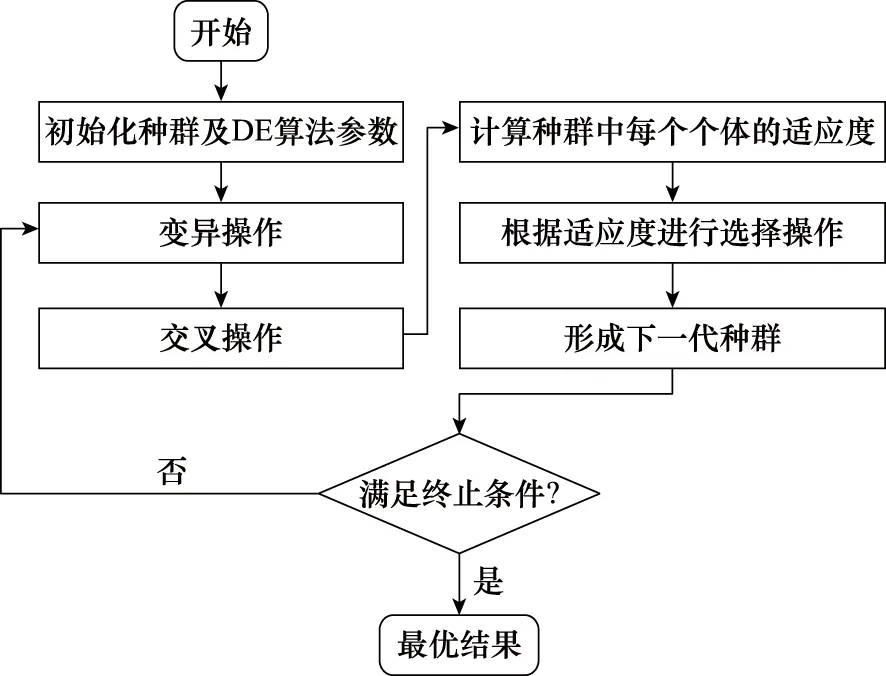
圖2 差分進化算法流程Fig.2 Process of differential evolution algorithm
本文模型的具體求解步驟如下。
步驟 1設定目標函數,生成初始種群,初始種群即在滿足約束條件的空間內隨機產生的n個可行解。
(13)
步驟 2進行變異操作與交叉操作。
變異操作:從種群中隨機選擇3個個體sa,sb,sc,采取DE/RAND/1變異策略:
μi(g+1)=sa(g)+F(sb(g)-sc(g)),i≠a≠b≠c
(14)
產生新個體。
式中:F為變異因子,用于縮放差分向量;sb(g)-sc(g)為差分向量。
交叉操作:交叉操作將新個體加入原始種群,提高種群的多樣性。
(15)
式中:randi(0,1)是[0,1]之間的隨機數;CR是交叉概率,取值[0,1],用于控制新個體替換父個體的程度。
步驟 3計算并比較目標函數值,如果目標函數值更優,則進行選擇操作進入下一代。
選擇操作:差分進化算法采用了貪婪的選擇策略。將通過變異和交叉操作生成的新個體與父個體的適應度進行比較,表現較好的進入下一代種群。
(16)
式中:函數f是適應度函數,即本文的目標函數,用于計算個體的適應度,衡量個體的優劣程度。如果新個體的適應度優于父個體,則將其引入種群,否則保留原個體。
步驟 4重復步驟2和步驟3,滿足終止條件時,輸出結果。
3 算例分析
為了對裝備維修保障工作提供技術支持,滿足裝備維修保障精準化、高效化、經濟化的要求,對某型裝備關鍵部件進行剩余壽命預測并給出儲備策略。現有240個參考裝備關鍵部件的全壽命綜合性能指標檢測數據(檢測間隔期15天),由于篇幅限制,部分數據如表1所示,當綜合性能指標值達到失效閾值0.7時部件壽命終止。20個服役裝備關鍵部件的部分早期檢測數據如表2所示。表1和表2中檢測序數反映出檢測時裝備關鍵部件的運行時間。對20個服役裝備關鍵部件進行剩余壽命預測,給出部件維修更換兩次時的經濟性儲備策略,假設初始庫存量為0,各項參數如表3所示。

表1 參考裝備關鍵部件全壽命綜合性能指標檢測數據Table 1 The whole life comprehensive performance index test data of reference key components of equipment

表2 服役裝備關鍵部件早期綜合性能指標檢測數據Table 2 Early comprehensive performance index test data of key components of equipment in service

表3 裝備部件維修保障參數Table 3 Maintenance support parameters of equipment component
3.1 基于改進相似性的裝備部件剩余壽命預測
3.1.1 剩余壽命預測
基于系統聚類的方法,根據裝備部件綜合性能指標的退化趨勢差異,對參考部件進行分類,區分不同的運行條件。根據聚合系數的變化率,將參考裝備關鍵部件分為4類,如圖3為第2類運行條件下裝備關鍵部件的全壽命綜合性能指標檢測數據及其聚類中心。4類運行條件下裝備部件綜合性能指標狀態的聚類中心如圖4所示。將參考裝備關鍵部件的全壽命性能狀態檢測數據作為訓練集輸入,分類結果作為訓練集輸出,對GA-BP網絡進行訓練。將服役裝備關鍵部件的早期性能狀態檢測數據作為測試集輸入,通過訓練好的GA-BP網絡得到其分類結果,如表4所示。
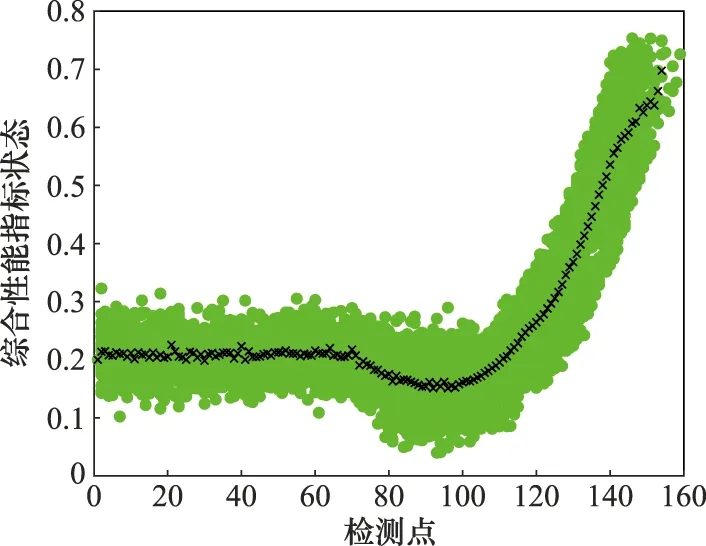
圖3 第2類裝備關鍵部件及其聚類中心Fig.3 Category 2 equipment key components and theirs clustering center
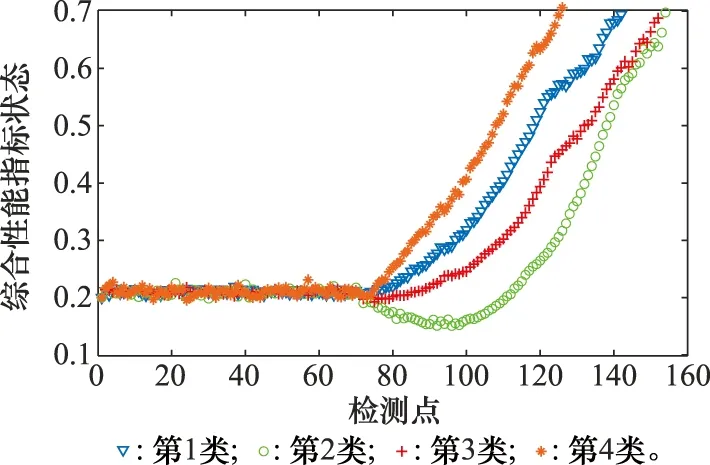
圖4 4類裝備關鍵部件聚類中心Fig.4 Cluster center for key components of four categories of equipment

表4 服役裝備關鍵部件分類結果Table 4 Classification results of key components of equipment in service
基于上述裝備部件的分類結果,對各類別內裝備部件的全壽命綜合性能指標檢測數據進行處理,得到參考裝備關鍵部件的失效壽命。根據式(1)和式(2)計算各類別內服役部件與各參考部件之間的歐氏距離,確定相似度。根據式(3)確定不同參考部件的權重。根據式(4)確定各服役部件的剩余壽命。剩余壽命預測結果如表5所示。
3.1.2 相對誤差分析
為了分析該剩余壽命預測模型的相對誤差,從240個參考部件中隨機抽取20個作為樣本,通過本文的剩余壽命預測模型進行剩余壽命預測,得到壽命預測值后與其真實的失效壽命對比計算相對誤差。為便于分析,將本文提出的基于改進相似性的裝備部件剩余壽命預測方法記為M0;將采用傳統的基于相似性的裝備部件剩余壽命預測方法,即認為參考部件自身及其與服役部件運行條件相同的方法引入本文模型,記為M1。進一步可知,M0與M1主要區別在于是否考慮了裝備部件運行條件的差異、是否對裝備部件進行分類。相對誤差分析結果如表6所示。
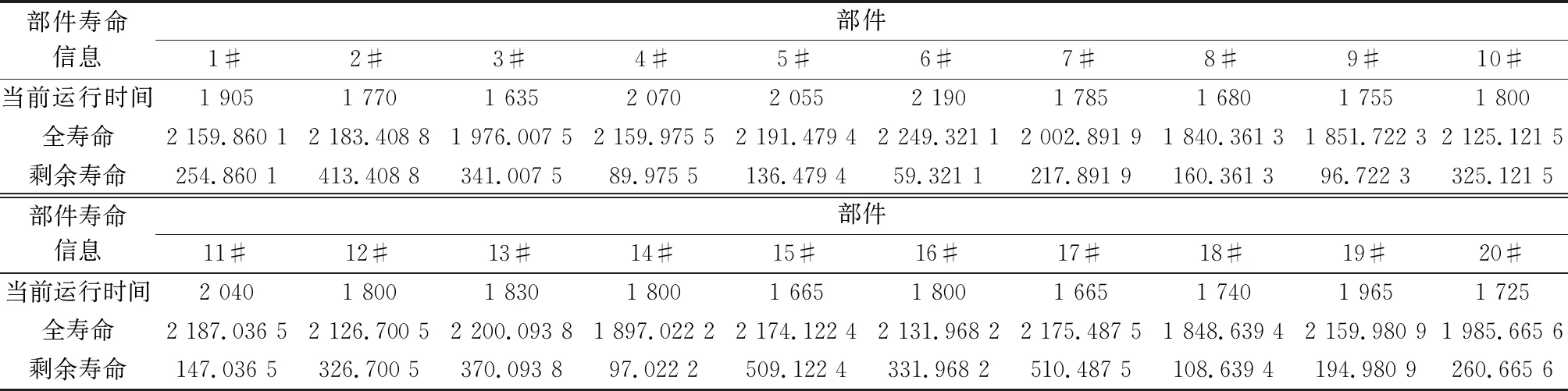
表5 服役裝備關鍵部件剩余壽命預測結果Table 5 Results of useful lifetime prediction of key components of equipment in service
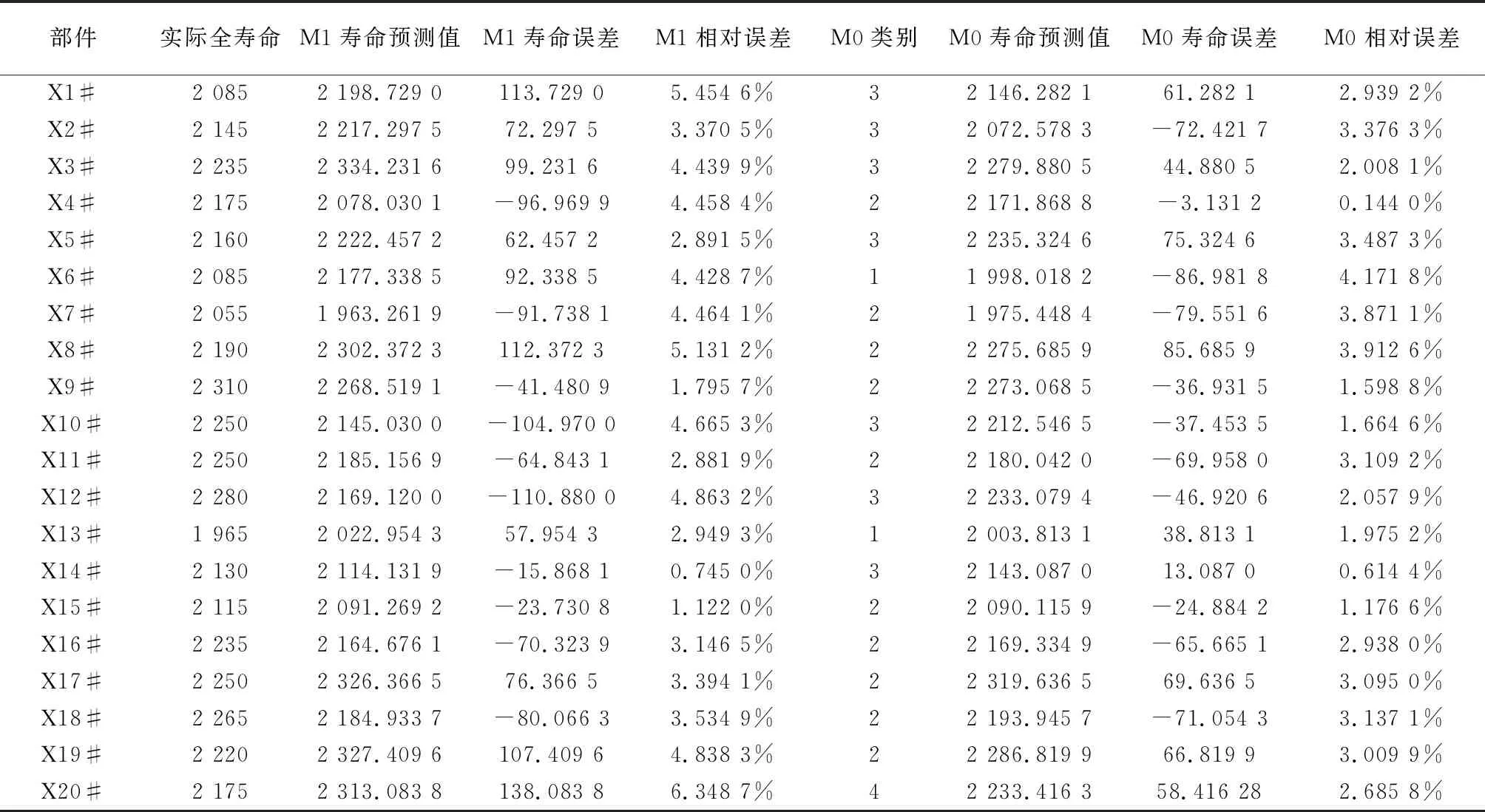
表6 剩余壽命預測相對誤差分析Table 6 Relative error analysis of useful lifetime prediction
由表6可知,M1的剩余壽命預測結果相對誤差均值為3.746 2%,M0的剩余壽命預測結果相對誤差均值為2.548 6%,該結果不僅說明了本文提出的基于改進相似性的剩余壽命預測模型的預測結果較為可信,且驗證了方法的合理性與科學性。
由表6可知,本文所提方法的剩余壽命預測值更接近于裝備部件的真實剩余壽命,準確度較高。究其原因,本文在基于相似性方法對裝備部件剩余壽命預測時考慮了參考部件及服役部件的運行環境條件差異,將運行條件近似的裝備部件進行聚類,類內裝備部件性能退化趨勢趨于一致,因此相似度較高,進而剩余壽命預測精度較高。而M1未考慮對參考部件和服役部件的運行條件進行區分,使用全數參考部件進行相似度度量及剩余壽命的預測,使得運行條件不同的相似度較小的樣本對結果產生影響,導致剩余壽命預測值誤差的增大。因此,在基于相似性的剩余壽命預測時,有必要加入本文所提方法考慮的因素,對環境擾動導致的參考部件及服役部件的運行條件差異進行區分,提升預測的準確性。
3.2 基于剩余壽命信息的裝備部件經濟性儲備策略
根據裝備關鍵部件訂購儲備及維修更換費用的實際情況,有α=20,e1=300 萬元/個,e2=50 萬元/次,e3=5 萬元/(個·天),e4=0.5 萬元/(個·天),t1=60天,t2=180天。基于第3.1節所確定的裝備部件剩余壽命,將參數代入第2.1節所建立的模型,利用Matlab 2020a進行編程,使用差分進化算法對模型進行尋優求解,設定初始種群為100,迭代次數為1 000,進行仿真運算,得出結果。根據M0和M1所得裝備部件剩余壽命,分別進行目標函數的尋優并給出裝備部件經濟性儲備策略,觀察兩種方法對裝備部件經濟性儲備策略的影響及目標函數最優值的差別。
3.2.1 儲備策略及對比驗證
迭代尋優過程如圖5所示,表7和表8分別列出了M0和M1兩種方法所給出的裝備部件經濟性儲備策略,即服役部件更換兩次的訂貨時間點及訂購數量。
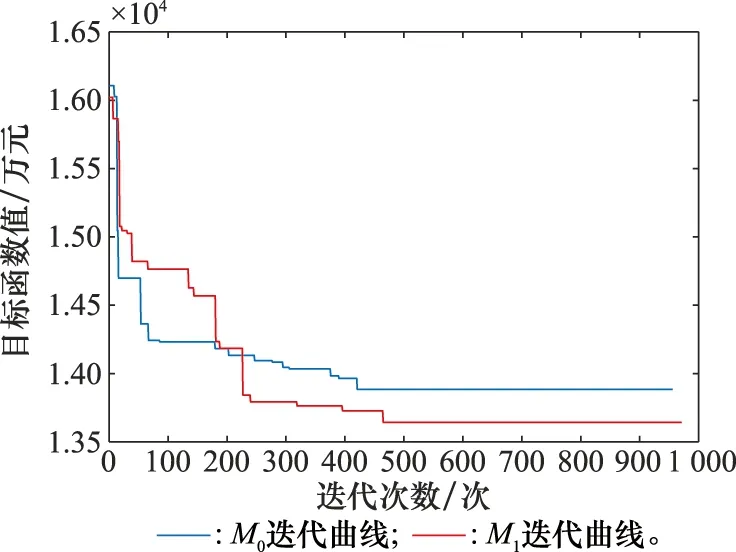
圖5 迭代尋優過程Fig.5 Process of iterative optimization
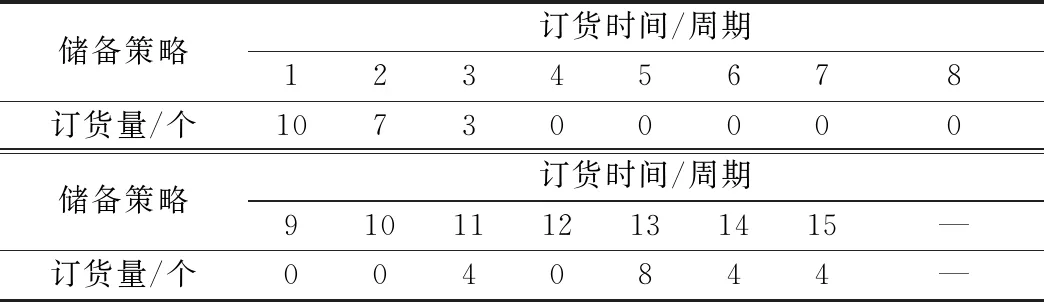
表7 M0所得裝備關鍵部件儲備策略Table 7 Reserve of key components of equipment obtained by M0
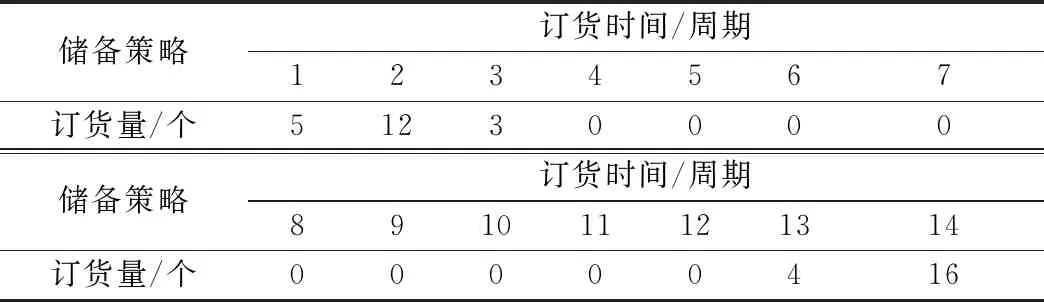
表8 M1所得裝備關鍵部件儲備策略Table 8 Reserve of key components of equipment obtained by M1
圖5給出了M0和M1的迭代尋優過程,由于兩種方法對裝備部件剩余壽命預測的準確度不同,導致了裝備部件經濟性儲備策略的差異,進而影響了目標函數即裝備部件維修儲備總費用。由圖5、表7及表8分析知,M0對應的裝備部件維修儲備單位周期費用為925.57萬元,M1對應的裝備部件維修儲備單位周期費用為974.46萬元,M0單位周期費用低于M1單位周期費用,進一步說明了M0對應的方法優于M1。究其原因,主要是由于M0的剩余壽命預測準確度要高于M1,導致M0較M1能夠更加準確地進行裝備部件的儲備與維修決策,提升了裝備部件維修保障的經濟性。上述結論體現了剩余壽命預測準確性對裝備部件儲備策略的重要影響,驗證了本文方法的合理性,因此在進行裝備部件剩余壽命預測時應考慮本文所提對相似性的改進。
3.2.2 靈敏度分析
在前文研究的基礎上,采用控制變量法對本文所提方法進行各項費用參數的靈敏度分析。選定t1=60天,t2=180天,由于e4 圖6 費用參數靈敏度分析Fig.6 Sensitivity analysis of cost parameters 由圖6可知,裝備部件維修儲備總費用隨著更換費用e1、訂貨費用e2、缺件損失費用e3、存儲費用e4的增加而提升,更換費用e1和存儲費用e4對裝備部件維修儲備總費用的影響較大。結果表明,裝備部件維修儲備總費用對更換費用e1和存儲費用e4的靈敏性較高,而對訂貨費用e2和缺件損失費用e3的靈敏性較低。進一步分析可以發現,更換費用e1、訂貨費用e2與裝備部件維修儲備總費用近似成線性關系,這是由于在其他條件確定時,部件的訂貨次數趨于穩定。當缺件損失費用e3較小時,裝備部件維修儲備總費用增加較快。而當缺件損失費用e3較大時,裝備部件維修儲備總費用增加則逐步平緩。其原因主要是當缺件損失較小時,為保證經濟性,會選擇對到壽的裝備部件進行失效后更換,以降低裝備部件維修儲備總費用。而當缺件損失較大時,則以存儲部件進行到壽更換為主導,裝備部件維修儲備總費用也趨于穩定。隨著存儲費用e4的提高,裝備部件維修儲備總費用的變化幅度逐步減小,但是減小幅度不明顯,原因是取缺件損失費用e3=5 萬元/(個·天)時,維修更換以儲備部件進行到壽更換為主導,因此存儲費用對裝備部件維修儲備總費用的影響變化率差異較小。 本文采用改進相似性構建了裝備部件剩余壽命預測模型,并在其基礎上得到了裝備部件經濟性儲備策略。具體結論有: (1)本文提出了考慮裝備部件運行條件差異的改進相似性剩余壽命預測方法,依據運行條件的差異性實現對裝備部件的分類,進而建立了剩余壽命預測模型,提升了預測的準確性。 (2)基于剩余壽命預測信息,建立裝備部件儲備策略決策模型。實例分析表明,準確的剩余壽命預測結果有助于實現維修決策及部件儲備策略的最優。 在裝備維修保障過程中,小樣本量的情況普遍存在,以小樣本為前提條件的基于相似性的剩余壽命預測方法及維修保障決策是今后的研究重點,以增強方法的適用性和普遍性。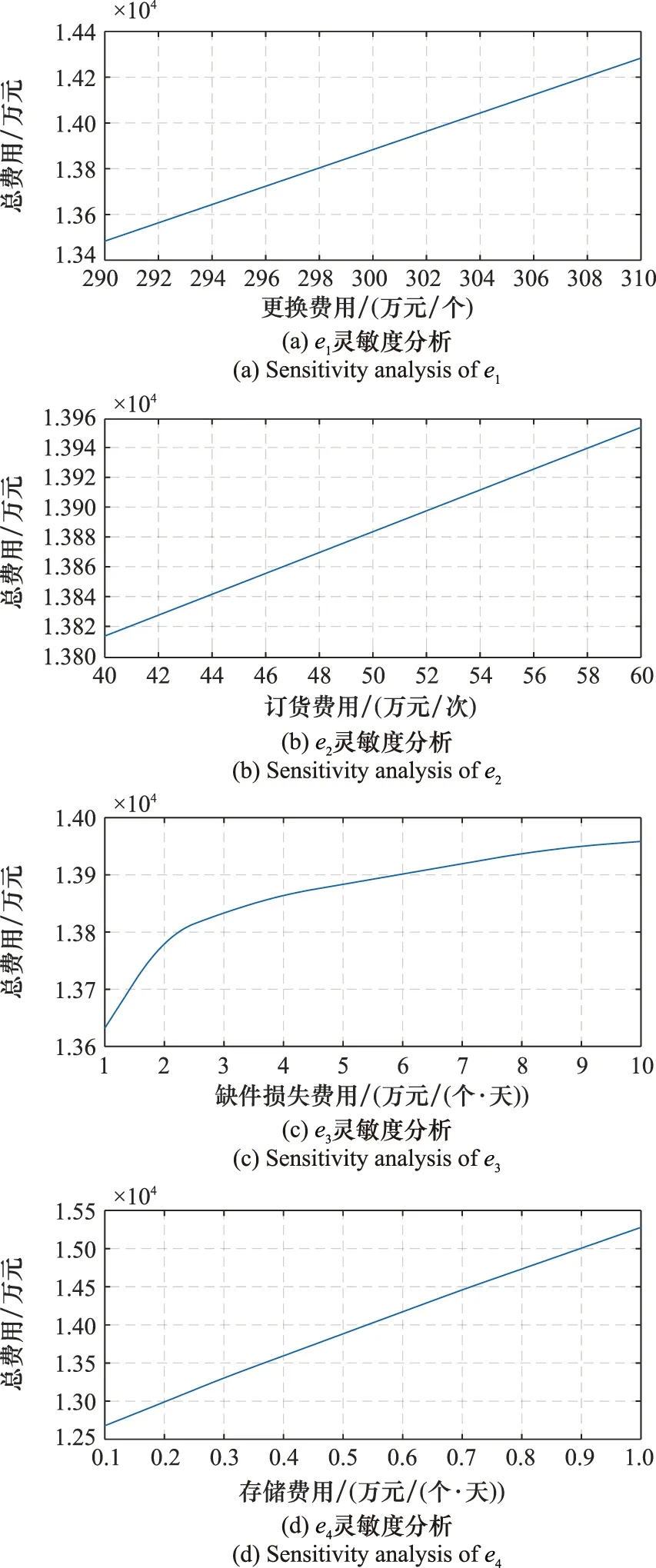
4 結 語

