基于Fe-safe軟件的轉葉式舵機疲勞分析及優化建議

韋紅錢 倪培源 端傳捷

（1.南京中船綠洲機器有限公司，南京 210000；2.河海大學 港口海岸與近海工程學院，南京 210000）

船舶舵機是重要的船舶操縱設備，其性能直接影響船舶的穩定性和安全性。隨著船舶制造業的飛速發展，船舶噸位越來越大，對舵機的要求越來越高。轉葉式舵機與其他舵機相比，具有結構緊湊、質量小、體積小、安裝方便、維護簡便、輸出扭矩不受轉舵角的影響以及控制性能好等優點[1]，因此一直備受人們的關注。

1 工作內容

計算內容包括產生疲勞裂紋的部位、產生疲勞裂紋的時間、工作應力作用下的安全因子及存活概率。輸出結果包括疲勞壽命分布、疲勞損傷分布、應力/應變時程以及裂紋方向等[2]。

Fe-safe作為一款疲勞分析軟件，計算前需要其他求解器的求解結果，如abaqus中的.fil文件和.odb文件、ansys中的.rst文件以及nastran中的op2文件等。將求解結果導入Fe-safe后建立載荷的時間歷程、材料及對應的S-N曲線，并定義表面粗糙度和算法等相關參數。計算后得到某一點處的循環周次，通過其他后處理軟件讀取相應的可視化結果。

2 舵機數值模型建立

舵機由缸體、缸蓋、靜葉、轉子、襯套、蓋板、推力軸承及螺栓等零件組成[3]。其中：螺栓1為連接缸蓋與缸體的36個12.9級螺栓；螺栓2為連接缸蓋與靜葉的6個8.8級螺栓；螺栓3為連接缸體與靜葉的6個8.8級螺栓；螺栓4為側面缸體與靜葉的12個8.8級螺栓，如圖1所示。缸體、缸蓋及靜葉的材料為球墨鑄鐵QT400-18，彈性模量為173 GPa，屈服強度為250 MPa；轉子的材料為球墨鑄鐵QT400，屈服強度為335 MPa；螺栓均采用45號合金鋼，彈性模量均為210 GPa；上下蓋板為Q235鋼；上述材料的泊松比均取0.3。

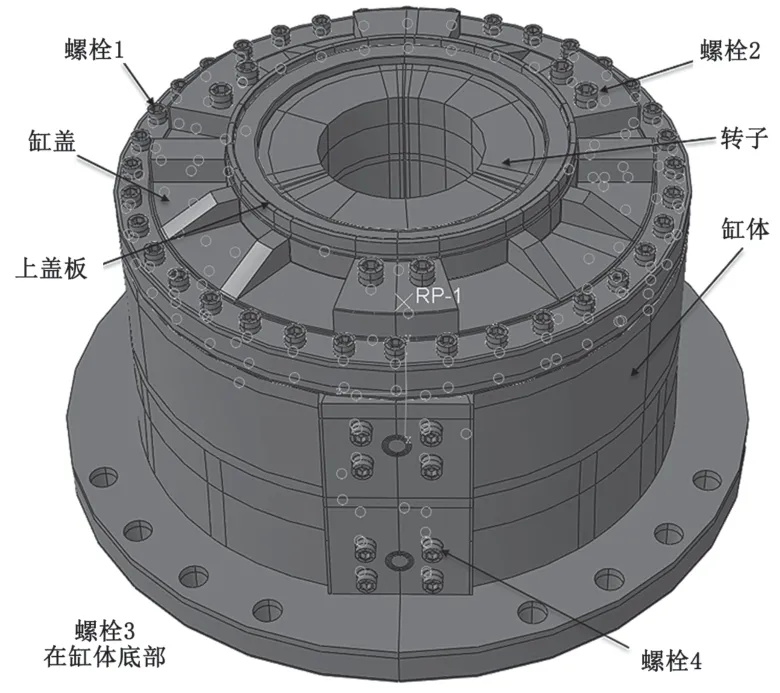
圖1 舵機整體模型示意圖

舵機各個部件表面的接觸關系可以分為摩擦接觸和綁定接觸兩類。摩擦接觸關系的表面主要包括螺栓1螺母底面與缸蓋頂面、螺栓2螺母底面與缸蓋加勁板的頂面、螺栓3螺母底面與缸體底加勁板頂面、螺栓4螺母底面與缸體、缸蓋部分底面與缸體頂面；綁定接觸關系的表面主要包括螺栓1螺桿側面與缸體螺孔內側面、螺栓2、3、4螺桿側面與靜葉螺孔內側面、上壓蓋與缸蓋的接觸表面、下壓蓋與缸體的接觸表面。本舵機模型采用六面體網格，單元類型為非協調八節點六面體單元。螺栓上存在預緊力，螺栓1上為 240 kN，螺栓2與螺栓3上為260 kN，螺栓4上為180 kN。

3 基于Fe-safe軟件的舵機部件疲勞壽命分析

3.1 影響疲勞的因素

影響疲勞的因素主要包括：①平均應力，平均應力越大，壽命越低，當平均應力為拉應力時，也是如此；②應力分布方式，高應力區較多的構件（如大直徑構件）更容易破壞；③載荷作用方式，如拉壓比彎曲更容易破壞；④構件表面因素，如表面光潔度等[4]。

3.2 Fe-safe軟件疲勞壽命計算方法

實際產品在工作過程中處于多軸應力狀態，且疲勞破壞都從構件表面開始。構件表面在多數情況下處于二向應力和三向應變狀態。因此，Fe-safe軟件更多地采用二軸分析方法，對構件進行力變-疲勞分析計算。Fe-safe推薦使用的疲勞裂紋產生條件，對延性金屬采用平均應力修正的Brown-Miller組合應變準則。該準則認為最大疲勞損傷發生于經受最大剪應變幅的平面，且損傷與該平面上作用的剪應變和正應變有關，對延性材料能提供較佳的計算結果。

由最大主應變準則和最大剪應變準則可假定：

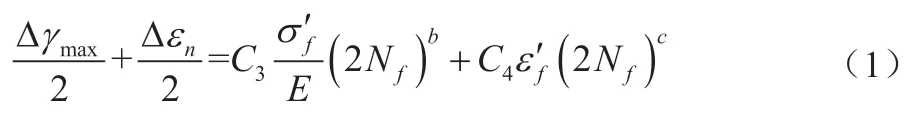
式中：Δεn為最大/最小剪應變平面上的正應變幅；Δγmax為最大剪應幅；2Nf為轉變壽命；σ′f為疲勞強度系數；ε′f為疲勞延性系數；b為疲勞強度指數；c為疲勞延性指數；E為彈性模量；C3、C4為系數。

對單軸應力有：

式中：ε1、ε2為主應變；ν為泊松比。

從而，有：

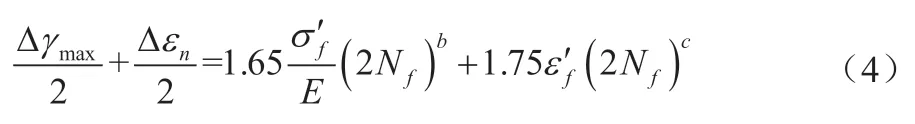
計算確定構件表面最容易出現疲勞破壞的平面和方向，也稱為臨界平面法。對主應力/主應變方向隨載荷歷程變化的情況，因很難確定哪個平面的應變循環范圍和循環次數最大，應采用臨界平面分析法計算一系列平面的應變和損傷，常用于主應變/主應力方向隨時間變化情況下的主應變/ 主應力、最大剪應變以及Brown-Miller疲勞壽命分析。

考慮平均應力的影響后，式（4）修正為：

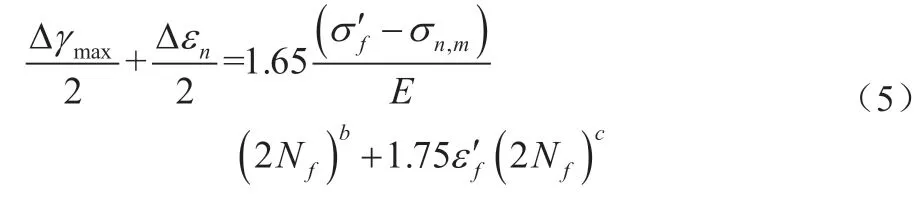
式中：σn,m為該平面上的平均正應力。

3.3 Fe-safe軟件疲勞壽命計算步驟

第一，讀入彈性計算的FEA應力張量（6個），用載荷歷程數據乘以應力張量，得到每個張量的歷程數據。第二，計算表面主應力的時間歷程（對接觸則考慮面外應力），從應力計算3個主應變的時間歷程數據。第三，采用臨界平面法，分析剪應變和Brown-Miller，在3個可能的平面上計算剪應變、法向應變、法向應力的時間歷程數據。第四，分析S-N曲線，定義一個臨界平面，計算垂直于該平面的時間歷程應力數據。第五，計算每個臨界平面的疲勞損傷，各平面的每種疲勞循環用雨流計數法統計，總損傷由每種循環的損傷疊加而成。具有最短壽命的平面即為裂紋發生平面，將其壽命寫入結果文件。第六，修正耐勞極限，如果臨界平面內的各種循環均低于耐勞極限，則沒有損傷產生。如果任一循環有損傷產生，則自動將耐勞極限降低25%。損傷曲線基于修正后的耐勞極限估算。此外，對每個單元都重復上述過程。

3.4 材料S-N曲線定義

采用S-N曲線計算該舵機的疲勞壽命，舵機主體材料為球墨鑄鐵QT400-18，與歐盟材料牌號為EN-GJS- 400-18的球鐵力學性能基本一致[1]，這里使用該材料的S-N曲線近似代替QT400 -18材料，對于螺栓、襯套、軸承及壓蓋在Total Material官網上查得其近似材料的S-N曲線。各材料使用的疲勞曲線分別如圖2～圖6所示，各曲線中的數據均具有97.7%的可靠度，其中循環次數的安全系數取5，應力范圍的安全系數取1.3。

圖2 QT400-18疲勞曲線

圖3 12.9級螺栓合金鋼疲勞曲線

圖6 壓蓋Q235-A疲勞曲線

圖4 銷軸、8.8級螺栓合金鋼疲勞曲線

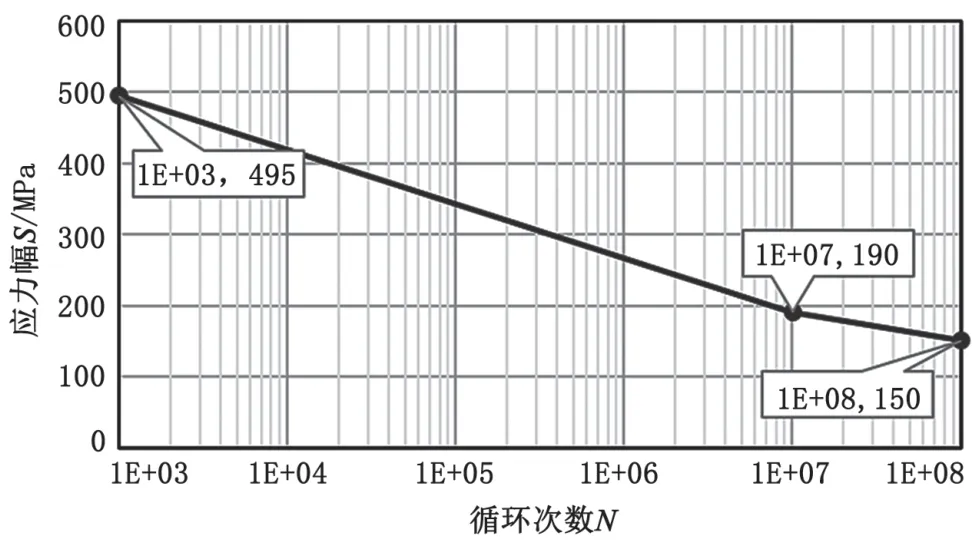
圖5 軸承ZCuAl10Fe3Mn2疲勞曲線

3.5疲勞荷載

舵機工作過程中，高壓腔與低壓腔循環交替。缸體、缸蓋、靜葉及轉子的受力面一直處于變化中，難以直接定義疲勞載荷。靜力分析也是對舵機整體進行的，由于存在較多的接觸問題，也難以簡單地對每個部件進行單獨分析（轉子除外）。因此，這里對除去轉子的舵機整體進行疲勞分析，轉子單獨分析。這里疲勞分析的有限元網格進行了局部加密，靜力分析總單元數約為25萬，疲勞分析的單元數約為60萬。由于載荷的方向、位置一直處于變化中，疲勞載荷不能簡單地用正弦曲線等來定義，這里按下述方法來定義。如圖7所示，這里主要的分析工況為：轉葉中心線左轉12°各節點的表面應力為s1，初始0°位置各節點的表面應力為s2，轉葉中心線右轉12°各節點的表面應力為s3，初始0°位置各節點的表面應力為s4，轉葉中心線左轉12°各節點的表面應力為s5。每個節點由s1→s2→s3→s4→s5→s1組成的應力譜即為特定工況下的疲勞載荷譜，對應的工作壓強為3 MPa，周期為18.4 s。

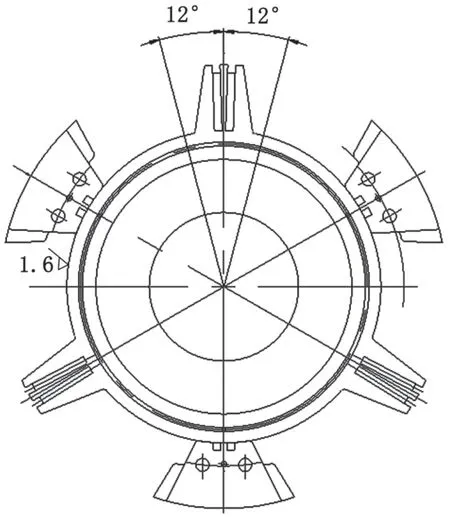
圖7 舵機疲勞工況

4 Fe-safe軟件疲勞壽命計算結果及分析

主要零部件的對數疲勞壽命（即logN）分布及疲勞安全因子分布結果如圖8～圖11所示。

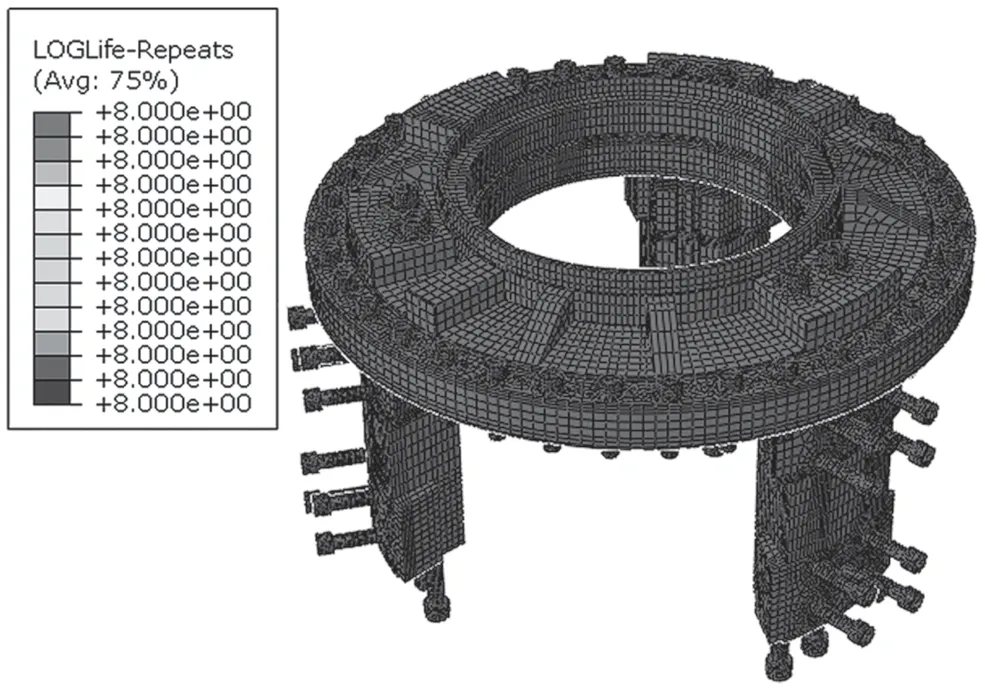
圖8 除缸體外舵機對數疲勞壽命分布

圖9 除缸體外舵機對數疲勞安全因子分布

從圖8～圖11可以看出，在3 MPa的工作壓強下，除缸體外所有部件疲勞壽命達到了耐勞極限值108次，缸體的疲勞壽命為106.992=9.82×106次。假定舵機每天工作24 h，一年按365天計算，最終算得缸體部分最小疲勞壽命約為81年，超過了舵機的設計使用壽命30年。S-N曲線計算得到的壽命一般為全壽命。對于純機械疲勞，裂紋萌生壽命一般在總壽命中占比約90%[2]，裂紋擴展壽命相對很短，因而最小裂紋萌生壽命為72.9年，大于設計壽命30年。實際在使用過程中，舵機尚未出現過裂紋，理論上在設計使用年限里不會出現裂紋，因此這里可不進行斷裂分析。

圖10 缸體對數疲勞壽命分布

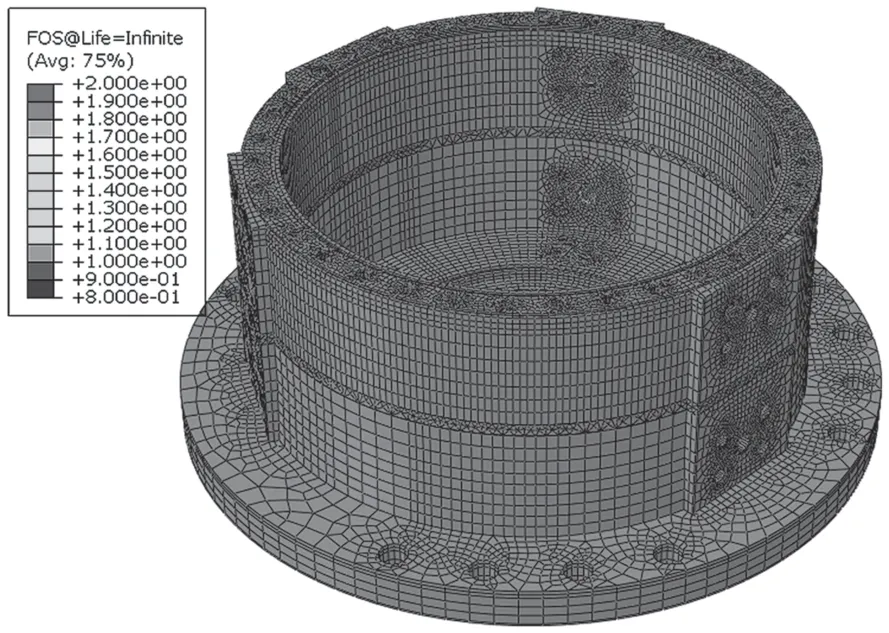
圖11 缸體對數疲勞安全因子分布

當作用的載荷幅低于某容許值時，構件不會產生疲勞破壞，將該容許值稱為構件的耐勞極限幅值。對于鋼材，一般以107次為失效循環允許的載荷施加次數。這里舵機整體以QT400-18球墨鑄鐵為主，材料的綜合性能與鋼接近，因而可近似取其疲勞壽命為107次。對于極其重要的零件設計，一般控制應力S，使其小于無限壽命（Nf=106）對應的耐勞極限Sf，該種疲勞設計方法稱為無限壽命設計。該設計方法的構件應力水平要求很低，無法充分發揮材料潛力，對于并不需要經受很多循環次數的構件，經濟性較低。

5 結語

本研究基于S-N曲線，采用Fe-safe軟件分別分析了800 kN·m轉葉式舵機各個部件的疲勞壽命。結果表明，所有部件的疲勞壽命均超過了設計使用壽命，屬于無限壽命設計，無法充分發揮材料的潛力，對于并不需要經受很多循環次數的構件，經濟性較低，可進一步考慮密封條和溫度的影響，通過優化設計，在不影響使用壽命的前提下進一步優化舵機結構。